含高温度梯度及接触热阻非线性热力耦合问题的谱元法1)
2022-08-26赵建宁杨苗苗张家雷刘冬欢
史 鑫 赵建宁 杨苗苗 张家雷 刘冬欢 ,2)
* (北京科技大学数理学院,磁光电复合材料与界面科学北京市重点实验室,北京 100083)
† (北京科技大学能源与环境工程学院,北京 100083)
** (中国工程物理研究院流体物理研究所,四川绵阳 621900)
引言
对于高超音速飞行器来说,由于急剧的气动加热在驻点区域会产生极高的温度梯度,并由此产生非线性热力耦合问题.求解此类问题的传统有限元方法往往采用低阶单元,因此需要在驻点区域采用相当密集的网格才能得到可信的结果[1].采用广义有限元方法是求解此类特殊问题的一个选择,O’Hara等[2-4]研究了广义有限元方法在存在局部高温度梯度的瞬态传热问题上的应用,在相对粗糙的网格上通过在局部区域附加特殊插值函数的方式来获得高精度解.文献[5-6]建立了局部加热引起的高温度梯度及高强应力应变问题的广义有限元方法,通过局部加密网格和插值函数升阶的方法来捕捉场变量的局部高梯度效应.Tang 等[7]提出了一种广义有限元方法来求解热传递及热弹性问题,通过采用高阶的插值函数来保证单元边界上温度梯度的连续性.Sanchez 和Duarte[8]建立了高阶广义有限元方法并将其用于多尺度结构动力学和波动问题的求解.Kim 等[9]很早就指出广义有限元方法潜在的缺点是如果局部网格加密或者插值函数升阶不当,那么会带来更大误差.Calabrò等[10]提出了一种求解高梯度椭圆方程的机器学习策略.Peng[11]针对高梯度问题提出了一种基于最小二乘法的新型扩展有限元方法,可以有效提高数值解的精度但是其收敛性会下降.对于此类高温度梯度问题也可以直接采用高阶p 型有限元方法[12].p 型有限元方法一般利用Lagrange多项式作为插值函数,且插值结点是等距分布的,对于高阶插值存在Runge现象.而谱方法[13]的插值函数采用插值结点非等距分布的正交多项式,可以很好地避免Runge 现象,在波传播等周期性问题中得到了广泛的应用[14].谱方法的一个缺点是只能在规则区域上进行离散,限制了使用范围,而实际工程结构的求解域往往是非规则的.因此,将谱方法与有限元方法相结合而成的谱有限元法,既保留了谱方法的高精度与快速收敛性又具有有限元方法可以求解任意不规则区域的优异适应性,受到了研究者的广泛关注[15-16].谱有限元法的插值函数可以基于正交多项式,比如Legendre 多项式或者Chebyshev 多项式,也可以基于非等距结点的Lagrange 多项式,非等距的结点位置往往可以选取各种正交多项式的零点.Komatitsch[17]分别采用四边形和三角形谱单元分析了弹性波在二维结构中的传播行为.Kudela 等[18]基于Lagrange 多项式建立了一维杆、梁和二维平面谱单元的计算格式,并将数值结果与有限元计算结果和实验测试结果比较,验证了谱单元方法的高效性和高精度.Liu[19]基于Chebyshev 多项式构造了一种Mindlin 伪谱单元,并对板结构进行了静力、动力和波传播分析.谱元法在其他工程领域也得到了广泛的应用,比如Merzari[20]采用基于Gauss-Lobatto-Legendre 结点集的Lagrange 多项式的谱元法研究了核反应堆堆芯内部的涡流问题.Xu 等[21]基于第一类Chebyshev多项式的谱元法研究了功能梯度材料结构热弹性性能.刘玉柱[22]利用谱元法进行全波形反演,提高了反演算法的计算精度与效率.Zakian 和Bathe[23]采用基于Lobatto 结点集的Lagrange 多项式的谱元法研究了结构动力学问题,结合质量阵可对角化的特性以及时间积分的Noh-Bathe 格式,大大提高了计算精度和效率.
值得注意的是,对于工程结构中经常遇到的存在高温度梯度现象,此前的研究已经证明了高阶单元在捕捉局部高梯度现象中的优势[1],与此同时,固体界面的接触热阻也会导致界面上温度的跳变,这可以看作是一种广义的高温度梯度.本文建立可用于求解含高温度梯度及接触热阻的结构非线性热力耦合问题的谱元法计算格式,并通过数值算例验证本文方法和程序的有效性及精度,为解决此类非线性热力耦合问题提供了一种新的高效高精度方法.
1 热力耦合问题的谱元法格式
这里采用顺序耦合的方法建立热力耦合问题的谱元法格式,分别建立热传导问题和热应力问题的计算格式,通过数值迭代的方法得到热力耦合问题的解.
1.1 热传导问题
边界为 ∂Ω的区域 Ω 上的热传导问题的控制方程为
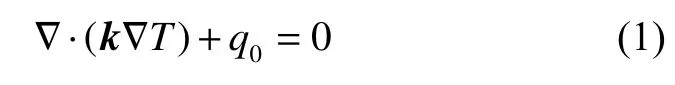
其中,∇ 为梯度算子,k是对称的热传导系数矩阵,T为温度,q0是热源函数.问题的Dirichlet 边界条件和Neumann 边界条件分别为
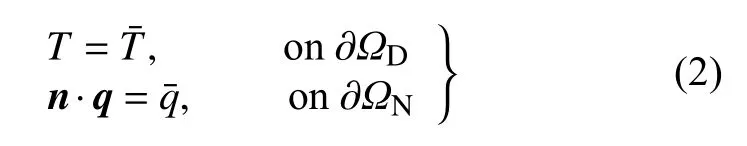
其中,∂ΩD和 ∂ΩN分别为Dirichlet 边界和Neumann边界,n为边界 ∂Ω的单位外法线向量,q为热流密度向量,分别为给定的温度值和热流密度值.
在单元域内方程(1)的等效积分弱形式为
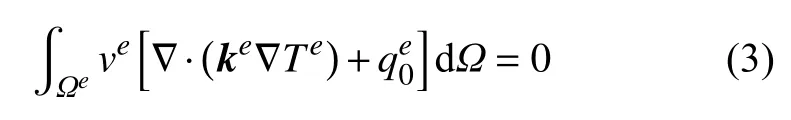
这里,ve为任意的权函数.
进一步考虑到
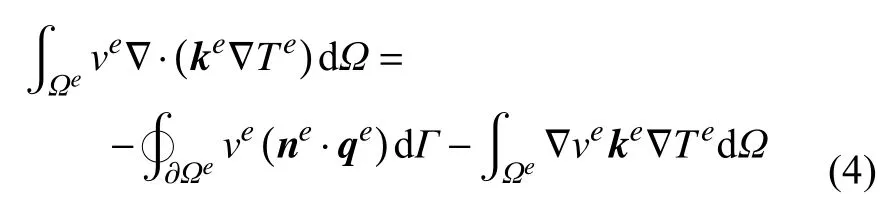
其中,热流密度为qe=-ke∇Te.将式(4)代入式(3)可得原问题的等效积分形式为

其中,ne为单元e的边界 ∂Ωe上的外法线.
方程(5)中出现了单元边界 ∂Ωe上的积分项,如果该单元边界是结构的外边界,那么热流可以由给定热流、对流换热或辐射换热等方式给出.而对于不存在接触热阻的单元内边界,该积分项会在组装总体有限元方程组时自动消除,此时热量平衡方程的等效积分形式为
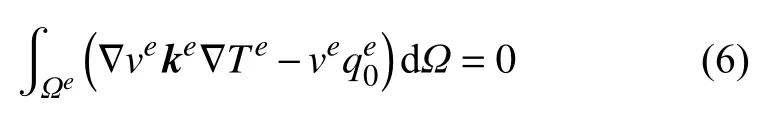
对于存在接触热阻R的单元内边界,采用间断有限元方法的处理思想[24],将接触界面处的热流密度由接触热阻的定义式给出
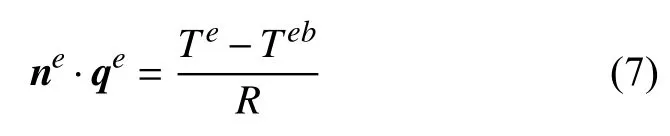
其中Te和Teb分别是界面两侧的温度.
与常规有限元方法一样,谱元法需要对单元内的场变量进行插值近似

本文采用Lagrange 型插值函数,其m阶一维形式为

传统的一维Lagrange 插值函数的插值结点在其插值区间上是等距均布的,而谱单元插值函数的结点是非等距分布的,这些非等距结点一般为Lobatto结点集或第二类Chebyshev 结点集[14].Lobatto 结点集即为Lobatto 多项式的零点,Lobatto 多项式是对Legendre 多项式进行求导得到的.第二类Chebyshev结点集即第二类Chebyshev 多项式的零点,其m+1个结点的坐标为:ξi=cos[(i-1)π/m] .基于不同结点集的前五阶Lagrange 插值函数图像如图1 所示.值得注意的是,也可以直接采用各种正交多项式比如Legendre 多项式或Chebyshev 多项式作为插值函数.
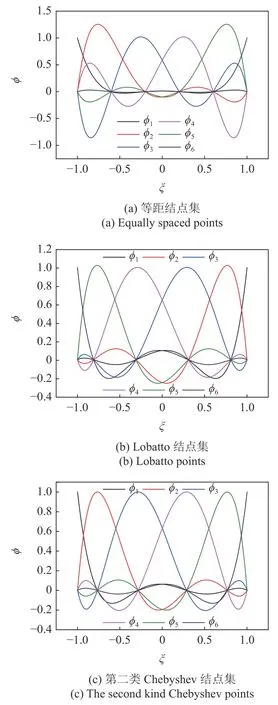
图1 基于不同结点集的Lagrange 插值函数Fig.1 Lagrange interpolation function with different interpolation points
二维Lagrange 插值函数可以利用ξ 和η 方向上的一维插值函数 φ(ξ)与 φ(η)的张量积得到,例如二阶二维Lagrange 插值函数可写为

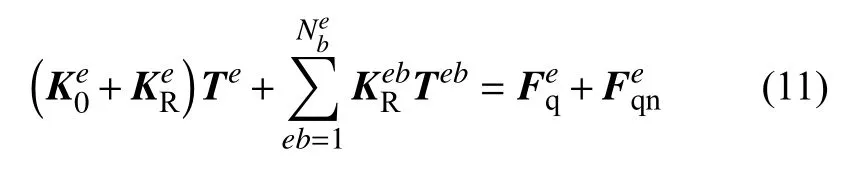
其中,域内热传导系数矩阵为
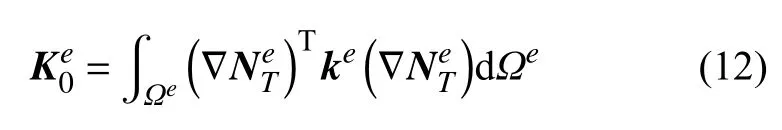
由单元内边界上接触热阻引起的与当前单元e及其邻居单元eb相关的系数矩阵分别为
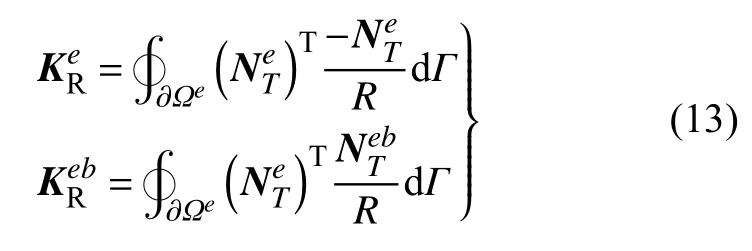
由单元域内热源项引起的等效热载荷为

由给定热流qn的边界条件引起的等效载荷列向量为
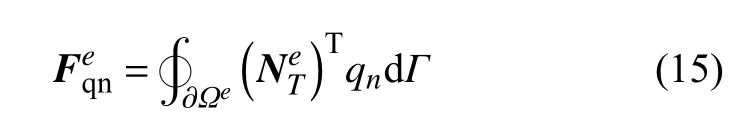
对单元有限元方程(11)进行组装,即可得到结构温度场分析的谱元法方程组

引入强制温度边界条件即可对方程组(16)进行求解,经过后处理即可得到结构的温度场和热流密度场.
1.2 热应力问题
结构热应力问题的平衡方程可写成

问题的Dirichlet 边界条件和Neumann 边界条件分别为
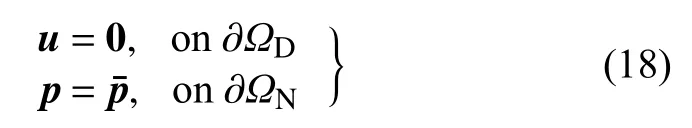
这里,σ 为应力向量,f为体力向量,u为位移向量,p为边界力向量.
考虑热变形的本构方程为

其中,De是弹性矩阵,T0是计算热变形的参考温度,εe为应变向量,αe是热膨胀系数向量.
与推导温度场控制方程的等效弱形式类似,力平衡方程的等效积分弱形式可写为
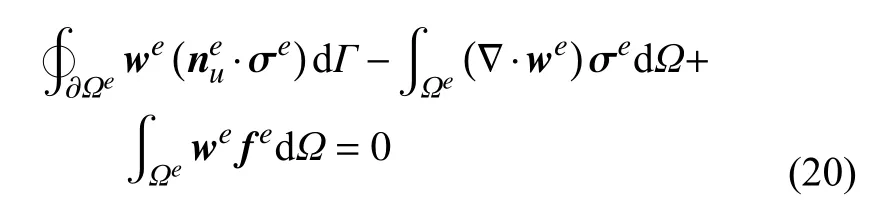
这里,we为单元位移场分析的权函数.
与温度场分析时在单元接触界面需要引入表征非完全热接触的接触热阻相对应,应力场分析时需要在接触界面上引入位移的不可穿透条件.这里采用共节点的处理方法.
在典型单元内位移场和应变场可分别表示成

位移场插值函数的推导与温度场类似,此处不再赘述.与温度场不同的是,对于平面二维问题,单元节点位移有两个基本未知量,因此位移场的插值函数为
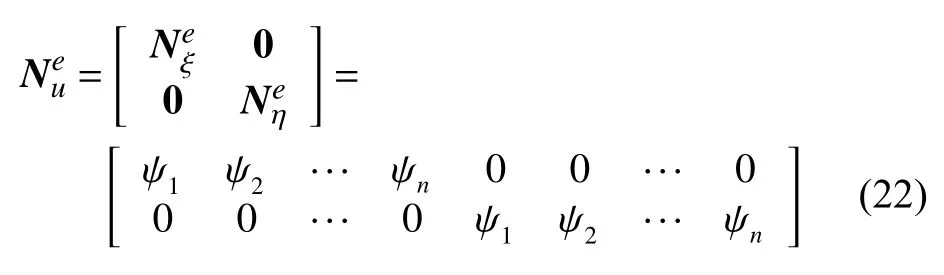
几何矩阵为
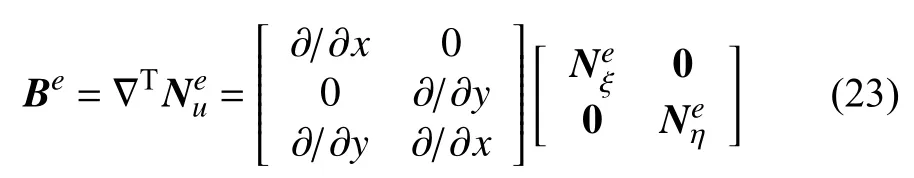
取权函数we=,并将几何方程和本构方程代入平衡方程,则位移场分析的单元有限元方程为

其中,域内刚度矩阵为

由体力引起的载荷列向量为

由温度场引起的载荷列向量为
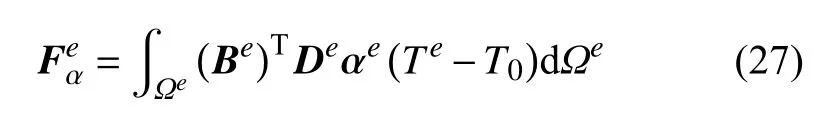
由力边界条件引起的载荷列向量
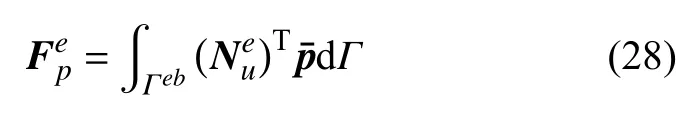
对单元有限元方程(24)进行组装,即可得到位移场分析的谱元法方程组

引入强制位移边界条件即可对方程组(29)进行求解,经过后处理即可得到结构的位移场和应力场.
1.3 谱元法的数值实现
以上系数矩阵的数值计算一般采用Gauss 积分法[25].对于采用正交多项式作为插值函数的谱元法,其系数矩阵计算时也可以利用插值函数的正交性而采用显式解析积分方案,有时能得到对角化的质量阵,对于瞬态问题来说,这是一个非常有用的特性[26].对于不同的正交多项式插值函数可以选择不同的积分方法,如果选择Lobatto 多项式作为插值函数,Gauss-Lobatto-Legendre 积分方法计算效率最高,而如果选择Chebyshev 多项式作为插值函数,Gauss-Legendre 积分方法计算效率最高.
本文对于存在应力相关接触热阻的热力耦合问题采用顺序耦合的方法进行迭代求解,即在初始假设的接触热阻条件下进行温度场分析,考虑到材料热导率的温度相关性,在温度场分析时也需要采用直接迭代法进行迭代求解,得到结构温度场之后进行结构位移场应力场分析,得到结构应力场之后对接触热阻和接触状态进行更新,然后再次进行温度场分析,待温度场和位移场同时满足收敛条件时迭代终止.整个的计算流程如下:
(1)输入几何、材料、载荷、边界条件及控制参数;
(2)初始化界面接触热阻R;
(3)基于设定的插值函数阶次,利用式(9)的张量积形式确定温度场插值函数;
(4)基于式(12)~式(15)得到单元有限元方程的系数矩阵,根据常规有限元方法组装总体有限元方程的方法,得到总体谱元法方程式(16);
(5)求解式(16)得到结构温度场,考虑到材料属性的温度相关性,反复迭代步骤4~5 得到收敛的温度场;
(7)基于结构应力场更新界面接触热阻,如果接触热阻达到收敛准则,则进入下一步,否则回到步骤4,进行新一轮迭代计算;
(8)输出结果,计算结束.
2 数值算例
本节给出三个数值算例来验证本文所建立的求解含高温度梯度及接触热阻的非线性热力耦合问题的谱元法的可行性及算法精度.
2.1 算例1
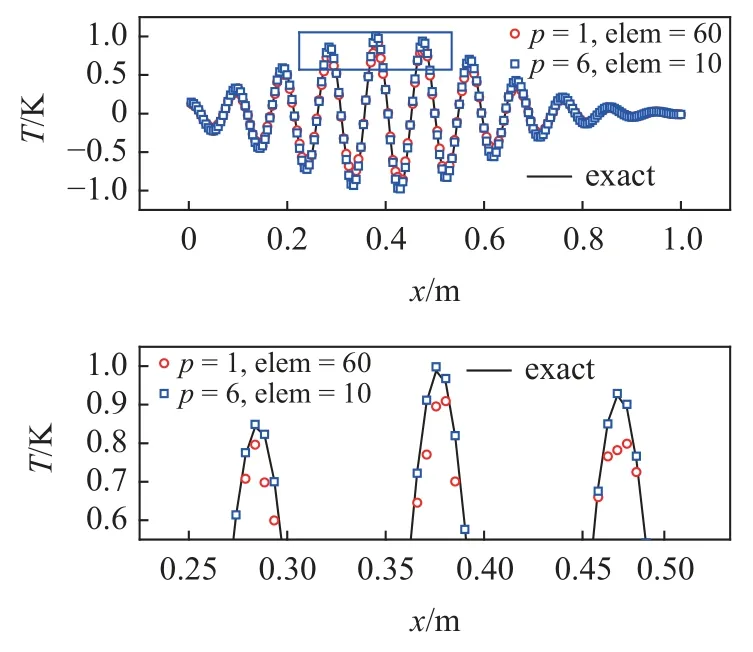
图2 一维热传递问题谱元法数值解与精确解的对比Fig.2 Comparisons of numerical results with spectral element method and exact solution for one-dimensional heat transfer problem
从图2 可以看出,谱单元可以用较少的单元数得到与精确解一致的结果,且能充分描述域内温度的剧烈变化.与此同时,和相同总自由度数目的经典线性单元相比,在捕捉温度峰值等细节上谱单元的精度更高.图3 进一步给出了不同阶次谱单元结果的收敛速度,这里采用的温度场2-范数误差定义为

其中,TSEM为谱元法计算得到的节点温度列向量,Texact为相同维度的节点温度列向量精确解.
图3 结果表明对于一维热传导问题,基于谱单元方法结果的收敛速度和计算精度都要高于经典线性单元,在总求解自由度数比较小的情况下,插值阶次越高则精度越好.而当总自由度数比较大时,温度场的2-范数误差并不总是最小的,这是因为自由度较高时基于各种插值阶次的计算精度都比较高,此时数值误差占主导,而插值函数和插值方法的误差处于次要地位.

图3 基于不同插值阶次谱单元的计算结果的收敛速度Fig.3 Convergency rate of numerical results with spectral element of different interpolation orders
2.2 算例2
考虑正方形域上的二维传热问题,正方形边长为6 m,其材料热导率为1 W/mK,四条边上保持恒定温度为0 K.其温度场的精确解为T(x,y)=,相应地,内生热率可由温度场的精确解求得.图4 给出了基于Lobatto 结点集的五阶谱单元得到的结构温度场与精确解的对比.图5 进一步给出了沿着x=1 和y=0 两条路径上温度分布的数值解与精确解的对比.
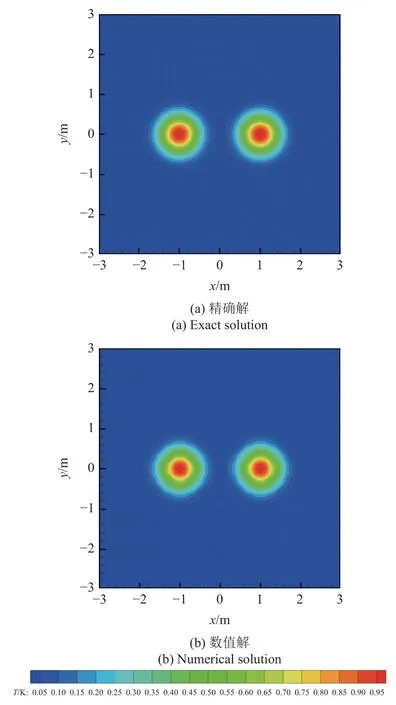
图4 二维热传递问题基于谱元法的温度场与精确解的对比Fig.4 Comparisons of numerical results with spectral element method and exact solution of the temperature field for two-dimensional heat transfer problem
从图4 和图5 可以看出,无论是定性比较还是定量比较,基于谱元法得到的数值解都和精确解吻合得很好.图6 进一步给出了采用等距结点的经典高阶有限元与采用Lobatto 和Chebyshev 非等距结点集的谱单元法得到的数值结果的收敛速度对比,从中可以明显看出,基于三种不同结点集的计算结果的收敛速度相差不大,但是在相同自由度的条件下,基于非等距结点集谱元法的精度更高,而且基于Lobatto 结点集的结果精度比基于Chebyshev 结点集的精度还要更好一些.

图5 沿x=1 和y=0 两条路径温度分布的数值解与精确解对比Fig.5 Comparisons of numerical results with spectral element method and exact solution for temperature distribution along x=1 and y=0

图6 基于不同结点集谱单元法的计算结果的收敛速度Fig.6 Convergency rate of numerical results with spectral element with different interpolation points
2.3 算例3
两块长度均为1 m 且宽度均为0.2 m 的矩形板沿长度方向对接在一起,组合结构的左端给定温度273 K,右端施加热流1000 W/m2.左右两端均固定.材料为45#钢,其弹性模量、泊松比、热膨胀系数和热导率均随温度变化[27].两块板的接触界面存在应力相关的接触热阻R=A0(σ/σ0)-2.5,其中A0=0.01 m2K/W,σ0=70 MPa,σ 为界面法向接触挤压应力,单位为MPa.
基于8 个矩形和四边形谱单元(有限元网格参见图7)计算得到的沿结构长度方向y=0 上的温度分布和x方向的位移分布与参考解的对比如图8 所示.这里参考解基于ANSYS 软件,采用了经过收敛性测试的100 000 个四节点平面应力单元.全场的温度分布和沿x方向位移、应力云图分别如图9~图11 所示.
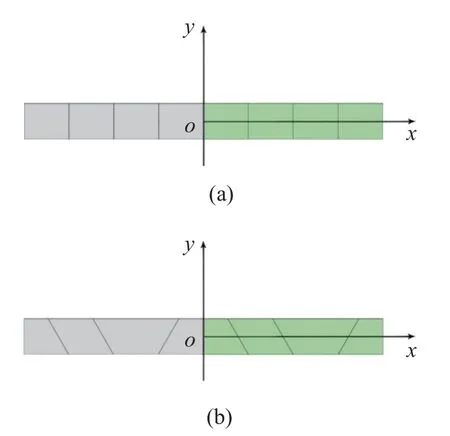
图7 矩形和四边形谱单元网格划分Fig.7 Spectral element with rectangular and quadrilateral mesh

图8 基于谱单元的计算结果与参考解的对比Fig.8 Comparisons of numerical solutions of spectral element with reference solution
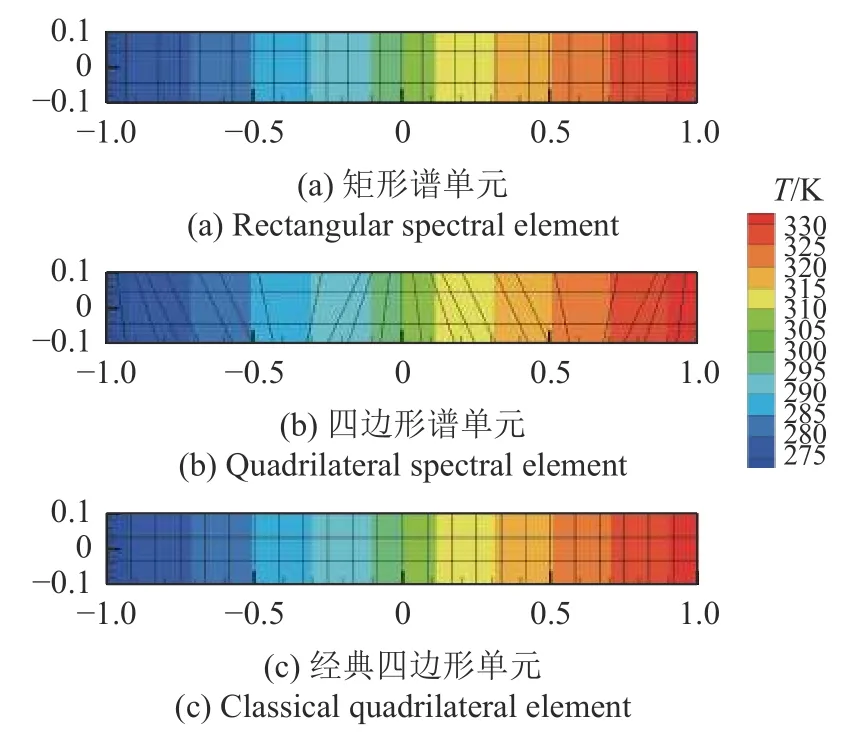
图9 基于三阶单元的结构温度场Fig.9 Numerical solutions of temperature field with third order element

图10 基于三阶单元的x 方向位移场Fig.10 Numerical solutions of displacement field along x-coordinate with third order element

图11 基于三阶谱单元的x 方向应力场Fig.11 Numerical solutions of stress field along x-coordinate with third order element
可以看出,无论是温度场还是水平方向的位移场和应力场,本文基于谱元法得到的计算结果都与参考解吻合得很好,由于两板接触界面上存在应力相关的接触热阻,因此这是一个非线性问题,需要进行迭代求解,由于接触热阻的存在,使得界面左右两侧出现了明显的温度跳变,如图8(a)所示.与此同时,无论是矩形谱单元还是任意四边形谱单元,计算结果都与参考解吻合得非常好,这表明本文方法在求解非线性热力耦合问题时具有良好的精度,相比传统谱方法只能在矩形单元上求解,谱元法很好地融合了谱方法和有限元方法的优点,可以有效地在不规则网格上求解,因此谱单元可以很好地应用在几何形状复杂的实际工程问题中.
数值计算时基于台式电脑Intel (R)Core (TM)i7-10750H CPU@2.60 GHz,由于对非线性问题需要迭代求解,因此计算时间较长.从表1 可以看出,无论是温度场还是位移场的相对误差,同样的总自由度(104)时高阶谱单元结果比经典线性单元精度更高用时更少,甚至高阶谱单元用更少的总自由度(104和170)得到了比线性单元采用更多自由度(210)更高的计算精度.与此同时,自由度总数为170 的高阶谱单元方法计算用时25.144 s,而自由度总数为104 的经典线性单元则用时61.557 s.这充分表明,本文提出的高阶谱单元方法,不仅利用较少的总自由度数即可得到高精度的计算结果,而且计算时间比耗费更多自由度的经典线性单元还要少,也即高阶谱单元兼有高精度和高效率的特点,在存在高温度梯度及接触热阻的非线性热力耦合问题上具有广阔的应用前景.
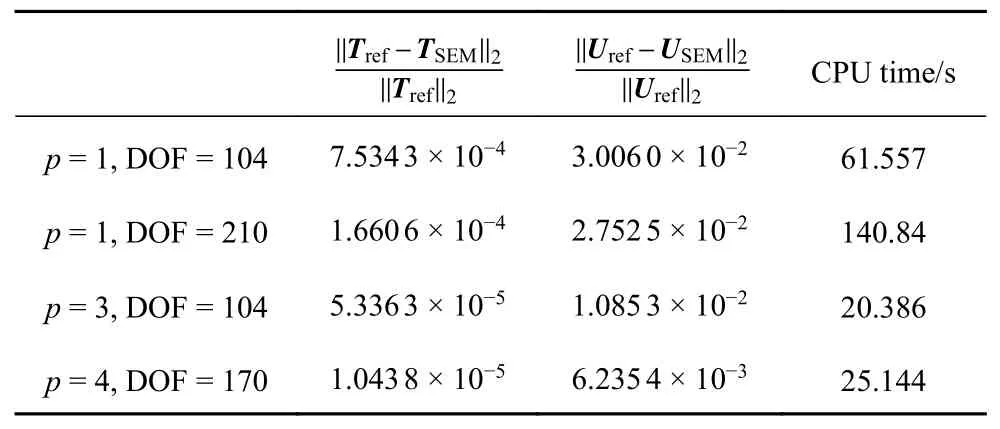
表1 不同网格及插值阶次谱元法的计算精度及计算时间Table 1 Computational accuracy and CPU time of spectral element method with different mesh grid and interpolation orders
进一步为了展示本文谱方法在三维热力耦合问题上的应用,保持本算例结构的长度和宽度不变,将厚度方向上的尺寸取为和结构宽度一样,材料属性、边界条件、载荷情况和界面参数等也保持不变.基于本文谱方法得到的计算结果与商用软件ANSYS 结果的对比如图12~图15 所示.

图12 结构温度场Fig.12 Temperature field
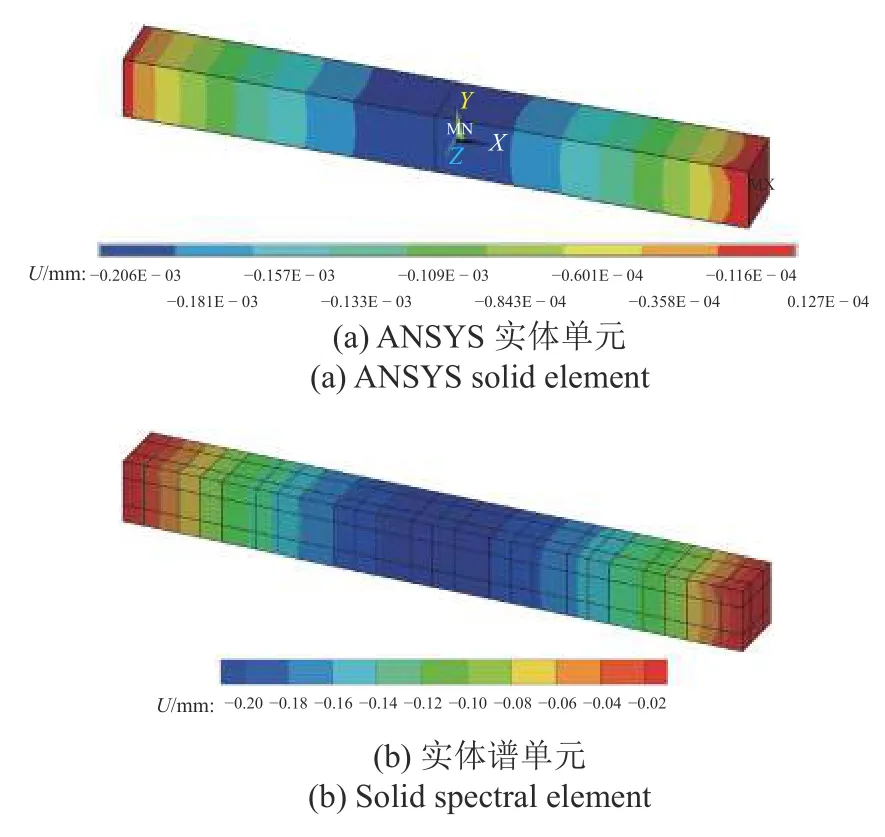
图13 结构x 方向位移场Fig.13 Displacement field along x-coordinate
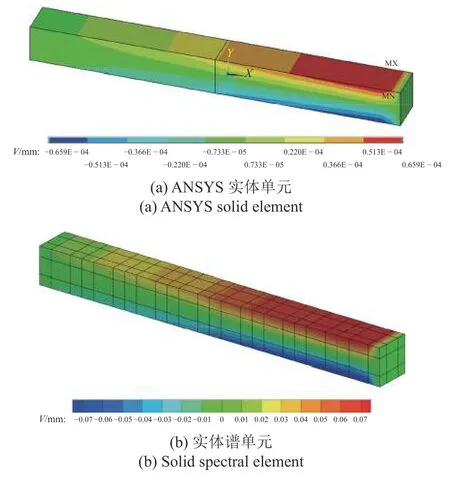
图14 结构y 方向位移场Fig.14 Displacement field along y-coordinate
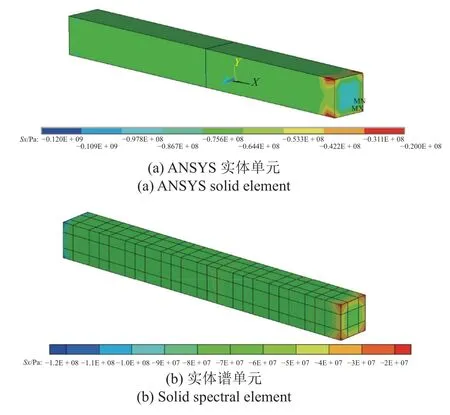
图15 结构x 方向应力场Fig.15 Stress field along x-coordinate
可以看出,针对三维热力耦合问题本文谱方法得到的结果和商用软件得到的结果吻合得很好,从而验证了本文谱方法在三维问题上的可行性和精度.
3 结论
基于Lobatto 及Chebyshev 非等距插值结点建立了Lagrange 型谱单元插值函数,并将其应用于存在高温度梯度及接触热阻的非线性热力耦合问题的求解,建立了相关谱元法的计算格式及计算流程,通过数值算例验证了本文建立的谱元法的计算精度及计算效率.数值结果表明:
(1)基于非等距结点的谱元法可以用较少的自由度捕捉到结构域内温度剧烈变化的趋势,计算精度和效率都比经典线性有限元法高;
(2)任意四边形单元的谱元法适用于几何形状复杂的实际工程问题,克服了传统谱方法只能使用矩形单元的弱点,适应性更强;
(3)对于含高温度梯度及接触热阻的非线性热力耦合问题,谱元法可以高效高精度地给出结构温度场及热变形热应力,具有广阔的工程应用前景.
值得注意的是,在本文研究中,虽然对场变量的插值函数采用了高阶格式,但是对单元几何场,采用了场变量插值函数一致的插值函数,存在一定的几何离散误差,下一步对几何场可以尝试采用非均匀有理NURBS 张量积为基函数进行近似[28],有望进一步将谱元法的优势发展到极致.
