基于数据驱动的全线控底盘纵臂式悬架系统研究1)
2022-08-26李全通杜秋月王翔宇詹伟梁尹思维
姚 淇 李全通 , 杜秋月 2) 陈 松 王翔宇 詹伟梁 尹思维 *
* (北京工商大学人工智能学院,北京 100048)
† (清华大学汽车安全与节能国家重点实验室,北京 100084)
** (湖南大学汽车车身先进设计制造国家重点实验室,长沙 410082)
†† (燕山大学机械工程学院,河北秦皇岛 066004)
*** (东风汽车股份有限公司商品研发院,武汉 430056)
引言
智能网联汽车逐渐成为汽车工业的研究热点,底盘线控执行控制成为其发展的关键技术[1].底盘动力学域控技术通过整合全车传感器信息,充分发挥出底盘性能[2].集成传统车辆驱动-制动-转向和主动悬架系统的全矢量底盘技术具有重要的发展潜力,车辆是一类典型的多系统耦合复杂非线性动力学系统[3],凭借其拥有更多的可控自由度从而更加有利于实现车辆的智能化控制[4].对于多自由度模型,当自由度取得越多时,理论上越逼近真实系统[5].从目前发展趋势以及各种驱动技术的特点来看,电动汽车是实现交通领域节能减排和污染防治的重要举措[6],全线控电动汽车成为解决复杂交通环境问题的重要工具,代表了未来电动汽车的发展趋势[7-8].
目前,车辆行驶平顺性正从随机路面、匀速直线行驶工况延展到凸台、凹坑、变速等越野极限工况[9],这对悬架系统性能提出了重要挑战,通过吸收和衰减来自路面不平而产生的振动和车轮波动,悬架系统可以让车辆平顺地行驶[10-11],其对车辆横向动力学密切相关的振动进行了阻尼作用[12].国内从20 世纪末开始对悬架运动学、弹性运动学,即K&C 特性进行系统研究[13].
李韶华等[14]搭建刚柔耦合的重型汽车整车模型,以车身垂向加速度和各轮垂向轮胎力为评价指标,提升了减速带连续通过的行驶平顺性.李小彭等[15]基于振动功率流理论对减振元件衬套进行优化选型,有效改善车辆悬架系统的综合减振性能.王震等[16]建立完整的机械-气体耦合多自由度动力学联合仿真模型,为侧翻事故发生率极高的全地形车设计了一种采用囊式空气弹簧的交叉型双气室空气互联悬架.纪秀业等[17]对悬架系统刚度与阻尼的匹配计算及验证,为后续悬架系统设计及操纵舒适性提升形成理论基础.张智等[18]对悬架的几何参数进行分析,以变化量处于更为合理范围内的车轮定位参数为目标进行优化设计.
王军年等[19]对传统汽车底盘进行电动轮改进,利用全局非归一化的多目标遗传优化算法对优化解集实现验证.李凡杰等[20]基于机电相似理论,对汽车悬架结构及参数进行优化设计,进一步提升了汽车悬架的减振性能.袁宝峰等[21]在摇臂式悬架的基础上,基于火星车地面力学等特点对主动悬架进行优化设计.张农等[22]对液压互联悬架的主要参数进行了全局灵敏度分析,通过NSGA-Ⅱ算法进行多目标优化,显著提升了综合性能.
陈龙等[23]建立新型悬架系统前轮定位参数的理论计算模型和多体动力学模型,解决传统悬架不适合轮毂驱动的难题.陆建辉等[24]将遗传优化算法与多体运动学分析方法相结合,对麦弗逊前悬架的设计参数进行优化.李芳[25]设计出改进型遗传算法对悬架参数进行了优化,提高了被动状态下的汽车性能.
本文从电动汽车线控技术的发展趋势出发,基于作者团队提出多自由度集成的全矢量概念,针对传统悬架方案存在的机械结构配合限位等相关问题,开展承载全矢量线控平台的双纵臂独立悬架结构方案设计,基于数据驱动背景,通过悬架子系统参数获取以及参数化设计变量的动态调整,进而确定最优方案.
1 一体化电动轮概述
传统汽车可控输入量较少,故对其动力学控制难度较大,路面的激励作用在单个车轮上可体现成3 个相对独立的力,从理论角度出发,传统四轮车辆系统的独立输入集合可扩展至12 个,基于此,作者团队提出如下定义:如果单个车轮的横向、纵向和垂向作用力都可进行独立控制,那么就称为全矢量控制(full vector control,FVC)汽车[1].作为自动驾驶的关键执行系统,线控技术可以实现代替驾驶员的物理操纵而对车辆发出行驶指令.传统的线控底盘未对车辆关键工作系统进行耦合协作,在此,作者团队设计驱动-制动-转向-悬架一体化的多功能电动轮系统,如图1,面向线控底盘技术,进一步提高整车灵活性和可控性.

图1 一体化电动轮结构图Fig.1 Integrated electric wheel structure diagram
一体化电动轮系统作为全矢量线控底盘的重要搭建板块,其对多子系统进行高度集成于一体,突破传统车辆单个系统间的耦合难题,进而实现全矢量线控技术给智能移动平台带来的技术空缺.对于多功能电动轮,其驱动系统采用高功率密度轮毂电机方案;制动系统采用再生制动与线控液压制动复合制动方式;转向系统采用转向电机经过减速器直接带动转向臂旋转方案,可实现车轮360°独立转向功能.
主动悬架对平顺性和操纵稳定性之间的冲突实现较好的平衡,显著提升乘坐舒适性和车辆行驶安全性[26-27],因此,本系统选取主动悬架为设计对象.悬架系统装配空气悬架可实现主动车身高度调节,装配磁流变阻尼器可实现阻尼线控调节,进而实现车轮垂向力的主动可控,悬架系统设计是本文重点开展研究的内容.
弹性元件采用空气弹簧形式,空气弹簧内部充满压缩空气,以压缩空气作为工作介质,满载工作压力通常为0.8 MPa 左右,当空气弹簧压缩时,气囊沿活塞座轮廓面向下挠曲变形[28].
磁流变阻尼器是一种阻尼可控的执行器,阻尼力可控范围大,响应时间可精确至毫秒级[29],因此,采用磁流变阻尼器作为悬架系统的减振器模块,凭借其特性,可实现对外部激励的有效吸能与缓冲减振.
簧下空间直接影响悬架系统的结构尺寸,一体化电动轮通过高密度轮毂电机实现驱制动,轮毂电机具有快速响应、转矩精确可控等特点,通过驱动转矩协调分配[30],簧下质量大导致轮胎动载荷增大,电机电磁力直接影响车辆垂向振动[31-32],使车轮动载荷变大,直接影响平顺性评价指标三个指标中的车轮相对动载,对电动汽车平顺性造成了一定的负面效应[33].为了解决上述问题,考虑簧下所占空间、搭载质量受一体化电动轮中轮毂电机的影响而发生量化,将转向中心线与转向电机轴线重合设计,即主销倾角设置为0,在不发生运动干涉的同时实现全方位转向.
2 悬架系统动力学与力学分析
2.1 车辆系统建模
本文搭建如图2 的车辆系统动力学模型,用以研究车辆垂向动力学的相关问题.采用7 DOF 动力学模型,包括车身垂向、俯仰和侧倾三个自由度;四个车轮独立垂向四个自由度,车辆坐标系为OXYZ.在下文中,FL,FR,RL 和 RR 或者数字 1~4 分别表示左前轮、右前轮、左后轮和右后轮.B为轮距,a和b分别为质心到前后轴距离.

图2 车辆系统垂向动力学模型Fig.2 Vehicle system vertical dynamics model
车辆与车轮垂向动力学模型

式中,z为车辆质心垂向位移;ms与mui为簧上质量与车轮质量;zui与zri为车轮垂向位移与路面输入;Fi为悬架力.
各悬架力可表示为

式中,ksi为悬架刚度系数,ci为悬架阻尼系数,Fai为空气悬架主动作动力,zsi悬架与车身安装点得垂向位移.
车身俯仰运动和侧倾运动微分方程为

式中,Ix和Iy为车身绕x和y轴的转动惯量,为俯仰、侧倾角加速度,ax和ay为纵、侧向加速度,hp和hr为车身质心到俯仰、侧倾中心的垂向距离.
当车身俯仰角较小时,悬架与车身连接点位的垂向位移与车身垂向位移的关系如下

式中,a为车辆质心到前轴距离,B为轮距,θ 为车身俯仰角,φ 为车身侧倾角.
2.2 悬架系统力学分析
根据总体设计方案,考虑结构紧凑、整车布置空间等建立出面向一体化电动轮系统的悬架结构如图3 所示.其中转向臂上端与整车转向机构相连,受转向电机作用力带动一体化电动轮做周转运动;双纵臂一端与转向臂铰接,另一端与转向节铰接,悬架工作过程中,分别绕铰接点做往复摆动,实现车轮的垂向行程;减振器上端与转向臂铰接相连,下端固定在下纵臂,装配轮毂电机、制动卡钳以实现驱、制动功能.其中,分别对6 处关键铰接位置进行命名,上下纵臂与转向节铰接处分别为A和B,与转向臂铰接处分别为D和C;减震器上端铰接点为O1,下端为O2.

图3 纵臂式悬架结构Fig.3 Trailing arm suspension structure
减振器作为悬架系统中重要工作部件,通过其往复运动实现对路面不平带来的冲击的缓冲,其安装位置应作首要考虑,通过对其进行静力学分析,可以判断出关键连接点的位置.根据减振器的结构尺寸,将减振器上端与转向臂铰接,下端与下纵臂进行铰接.保持上下纵臂静态位置时水平,则上纵臂在车轮纵向平面内并不受力,因此在对结构进行平面分析时,可将上纵臂略去.不考虑部件自身质量,当空气弹簧气囊压力一定时,在静平衡状态下可将减振器简化为受力连杆,结构简化如图4 所示.

图4 结构简图Fig.4 Structure diagram
其中B为转向节与下纵臂铰接点,O2为减振器下铰接点,C为下纵臂与转向臂的铰接点,O1为减振器上铰接点.L1为B和O2两铰接点的距离,L2为B和C两铰接点的距离,L3为减振器上下两铰接点的垂向距离,L4为减振器上铰接点到转向臂右侧距离,mg为单个电动轮载重,β为减振器倾斜角度,其中
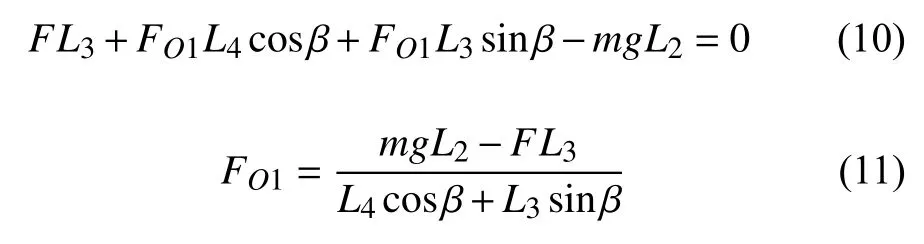
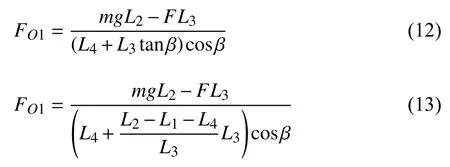
对于整个系统

故
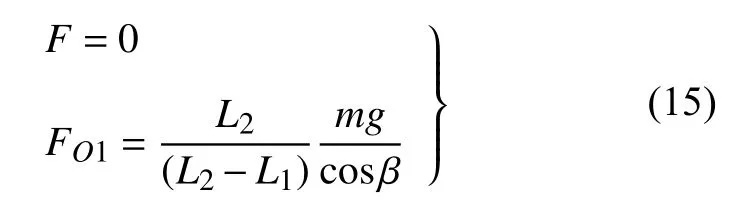
同理
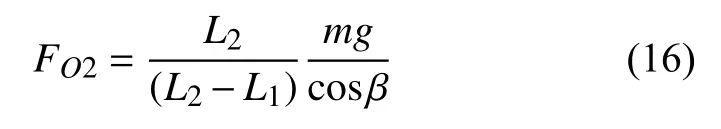
根据导向机构与减振器关键铰接位置的受力情况分析可以发现,影响减振器受力的主要因素是上下铰接位置,其之间的差异也就是安装角度.对减振器受力随其下端铰接位置的影响,可知下纵臂与转向臂铰接位置到其与转向节铰接位置间距在下纵臂总长中的占比越小,减振器受力越小,但结合本系统实现垂向行程可控范围最大化的设计目标,同时考虑过长的下纵臂导致转弯半径增加,降低灵活性.
3 悬架系统参数获取
3.1 磁流变阻尼器参数获取
磁流变阻尼器特性测试主要包括阻尼力特性测试及阻尼特性测试两方面,分别为:阻尼力Fd随位移X的变化关系和随速度v的变化关系.
假设振动试验台以100 次/分的振动频率给所测减振器施加正弦激励,测试行程X为100 mm (即振幅 ± 50 mm),则阻尼器测试行程位移为

活塞与缸筒的相对振动速度为

在某一时刻,阻尼系数乘以该时刻的活塞与缸筒的相对运动速度可以得到该时刻的阻尼力大小

因此,理想的阻尼器阻力特性曲线近似为关于行程位移X和阻尼力Fd的椭圆方程,该椭圆方程描述了给定位移的阻尼力大小.
对于磁流变阻尼器而言,改变电流可以获得阻尼力变化,因此阻尼系数并非恒定常数,但在一个循环周期内,其消耗能量的大小和被动阻尼器相等,磁流变阻尼器的等效阻尼系数为

同时,Wd也可写作如下形式

故磁流变阻尼器等效阻尼系数为

其中,Wd是一个周期内Fd-X曲线所围成的面积,表示阻尼器运动一个周期所消耗的能量,f为振动频率,Xmax为激励振幅.由于磁流变阻尼器是通过改变输入控制电流的大小来改变磁场,从而改变磁流变液的黏度,使阻尼系数获得大范围改变,从而提高磁流变阻尼器的耗能能力,可以获得磁流变阻尼器的阻尼力大小为

磁流变阻尼器的阻尼力大小和耗散能量Wd、振动频率f、振幅Xmax三个因素相关,由于耗散能量和控制电流输入大小相关,因此影响磁流变阻尼器阻尼力的直接因素主要包括控制电流i、振动频率f和振幅Xmax.
簧上质量与簧下质量相互远离时,需要较大的阻尼力消除振荡,在两者相互靠近时,需要较小的阻尼力减小对车架的冲击.在一个循环周期内,压缩阻尼力小于复原阻尼力,通过示功机可同时测出压缩阻尼力Fy和复原阻尼力Ff(图5).
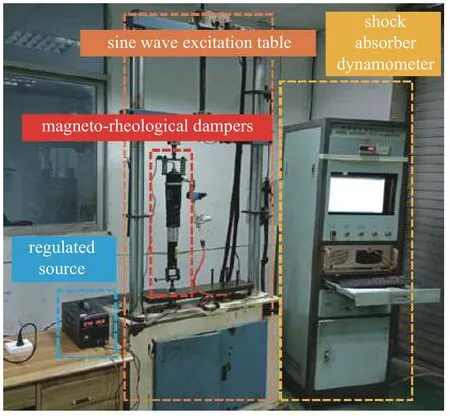
图5 磁流变阻尼器特性测试Fig.5 Magnetorheological damper characteristic test
取压缩阻尼力为

复原阻尼力为

其中β为伸缩系数,常取为10~15.
由于阻尼器内含有少量气体,需要测量出气体反拔力并在测试结果中去除,得到真实的油液阻尼力.在0~2.1 A 内以0.3 A 间隔改变施加于阻尼器的控制电流,固定振动频率为1 Hz,固定振幅为50 mm,获得的阻力特性曲线和阻尼特性曲线如图6~图7所示.

图6 阻尼力特性:变电流,固定频率1 Hz,振幅50 mmFig.6 Damping force characteristics:variable current,fixed frequency 1 Hz,amplitude 50 mm

图7 阻尼特性:变电流,固定频率1 Hz,振幅50 mmFig.7 Damping characteristics:variable current,fixed frequency 1 Hz,amplitude 50 mm
随电流以间隔0.3 A 增加,磁流变效应显著提升,屈服应力不断增加,示功曲线由内到外所围面积逐渐增大,表明阻尼器耗能能力增强.
从阻尼特性曲线看出,随电流增加,曲线斜率不断增加,表明电流的增加使得阻尼器阻尼不断变大.当电流增大到2.1 A 时,阻力相较于1.8 A 时变化已经不明显,表明磁流变阻尼器阻尼力变化已达到饱和,饱和电流为1.8 A.
因此,在对磁流变阻尼器进行控制时,可将电流调节范围限制在1.8 A 以下.同时可以看出在控制电流为0 时,减振器作为被动阻尼器的阻尼系数计算如下

由于气囊在筒壁上卷曲时具有一定的摩擦阻力和材料卷曲阻尼,根据经验适当增大阻尼系数,获得最终的被动阻尼器阻尼系数

在0.5~2.5 Hz 内以0.5 Hz 间隔改变施加于阻尼器的激励频率,固定控制电流为1 A,固定振幅为50 mm,获得的阻力特性曲线和阻尼特性曲线如图8~图9 所示.

图8 阻尼力特性:变频率,固定电流0.6 A,振幅50 mmFig.8 Damping force characteristics:variable frequency,fixed current 0.6 A,amplitude 50 mm

图9 阻尼特性:变频率,固定电流0.6 A,振幅50 mmFig.9 Damping characteristics:variable frequency,fixed current 0.6 A,amplitude 50 mm
通过改变振动频率,示功曲线所围面积增加,最大阻尼力也逐渐增大,表明磁流变阻尼器对外界振动频率较为敏感,而外界振动来源于路面起伏,使得悬架动挠度发生改变,造成簧上与簧下质量相对运动速度变化,相对运动速度变化越快,则需要更多的能量来衰减振动,从而使得最大阻尼力不断增大.
在10~50 mm 内以20 mm 间隔改变施加于阻尼器的振幅,固定控制电流为0.3 A,固定振动频率为1 Hz,获得的阻力特性曲线和阻尼特性曲线如图10 和图11 所示.

图10 阻尼力特性:变振幅,固定电流0.3 A,频率1 HzFig.10 Damping force characteristics:variable amplitude,fixed current 0.3 A,frequency 1 Hz

图11 阻尼特性:变振幅,固定电流0.3 A,频率1 HzFig.11 Damping characteristics:variable amplitude,fixed current 0.3 A,frequency 1 Hz
综上所述,通过三组实验测试结果分析了控制电流i,振动频率f和振动幅度Xmax对阻尼力大小的影响,由于控制电流i,振动频率f的变化对阻尼力的影响远大于振动幅度Xmax的变化,因此,本文仅将控制电流i和振动频率f作为磁流变阻尼器模型的两输入,对这两种因素进行适当控制,最终获得期望的阻尼力,故将磁流变阻尼器视作双输入单输出非线性模型,其中建立正向模型表达式如下
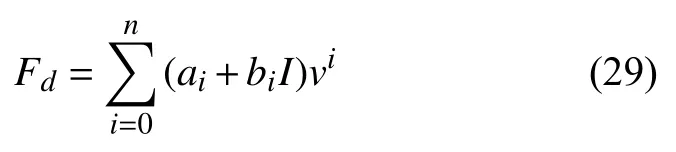
其中,Fd为磁流变阻尼力大小,I为电流幅值,v为阻尼器活塞速度,ai和bi为模型系数,n为模型阶次,为同时保证拟合精度并降低拟合难度,取n=7.建立逆向模型表达式为

3.2 空气弹簧参数获取
设置正弦波激振台振动频率为0.02 Hz,同时测试过程中保证气路的密闭性,充入最大气压设置为0.6 MPa 且采用最大伸张状态下单向激励的方式进行实验,弹簧初始高度为140 mm,记录不同充气压力下空气弹簧作用力和囊内气压随弹簧高度变化间的关系,计算出此时空气弹簧有效面积如表1.

表1 空气弹簧测试结果Table 1 Air spring test results
通过三次样条曲线拟合获得空气弹簧作用力和囊内气压随空气弹簧高度变化的关系,如图12 和图13所示.

图12 空气弹簧压力随空气弹簧高度变化的关系Fig.12 The relationship between air spring pressure and air spring height

图13 空气弹簧作用力随空气弹簧高度变化的关系Fig.13 The relationship between the force of the air spring and the height of the air spring
三次样条拟合模型表达式为

根据数据拟合得到初始压力为0.3 和0.6 MPa气囊内压力随高度的变化关系式如下

三次样条拟合模型表达式为
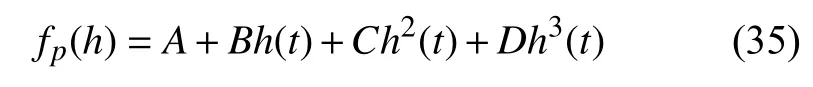
根据数据拟合得到初始压力分别为0.3 和0.6 MPa时空气弹簧作用力随高度的变化关系式如下
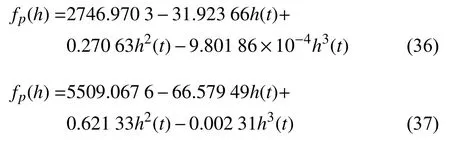
可以发现,充入0.6 MPa 时拟合得到的曲线形状和0.3 MPa 的很类似,两者相差2 倍.得到充入初始压力为xMPa 时,空气弹簧作用力随高度的变化关系式如下
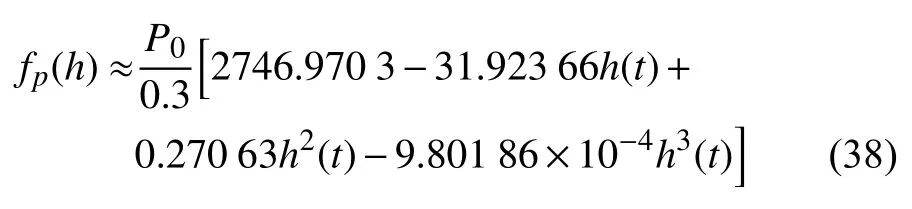
充入初始压力后,假设充入0.6 MPa 且达到静态平衡位置后,任一时刻空气弹簧作用力和弹簧高度直接相关.则充入初始压力P0后的弹簧刚度随高度的变化如下

由于高度为140 mm 时的数据点相比于其余测试数据点偏差较大,在拟合时将其屏蔽,得到初始压力分别为0.3 和0.6 MPa 时空气弹簧有效面积随高度的变化关系式及有效面积变化率如下

可以发现有效面积基本上都是关于弹簧高度线性变化的,且和囊内初始气压大小无关.综合两种初始气压实验结果,因此可以获得空气弹簧有效面积变化率

综上所述,可将空气弹簧也抽象称为双输入单输出的非线性模型,即空气弹簧刚度大小和囊内初始气压及气囊高度有关,囊内初始气压、气囊高度可根据悬架气压传感器和高度传感器进行实时测量得到,最终得到弹簧刚度值.
4 仿真验证与实物验证
4.1 参数化模型搭建
基于上文建立的悬架三维模型进行运动学仿真分析,引入数据驱动下的参数化变量设计.三维物理模型输入运动学仿真环境后,首先对悬架系统的关键硬点坐标进行确定,这里包括:上、下纵臂与转向节铰接位置、上下纵臂与转向臂铰接位置、减振器上下两端铰接位置共6 处关键硬点.通过对上述6 个关键铰接位置的参数化变量设计,可以得到多组不同数据对车轮垂向运动特性的影响对比,较高的可调整性有利于最优位置参数的确定.双臂间距通过调整A和D两点的z坐标值;臂长度通过调整A和B两点y坐标值;减振器上铰接O1处通过调整y坐标值;减振器下铰接O2处通过调整x坐标值.基础悬架空间位置坐标如表2.

表2 基础悬架空间位置坐标值(X,Y,Z)Table 2 The coordinate value of the space position of the base suspension (X,Y,Z)
运动学问题仿真环境下,进行对象融合时,将零部件定义为刚体;忽略运动副间摩擦.由于设计初期将主销倾角定义为0,故重点开展结构参数与车轮外倾角之间的关系,同时对悬架工作过程中车轮动能以及纵向位移进行综合考虑.
4.2 参数化增量分析
基于上文对减振器安装位置的初步确定,将基础铰接位置参数进行调整,其中减振器下铰接位置沿纵向调整3.3 mm.首先展开对减振器安装角度对上下铰接位置的力学影响.通过对上铰接位置做正、负增量调整来实现多角度状态对比,得到结果如图14.

图14 减振器角度对 O1和 O2 处受力影响Fig.14 The impact of the shock absorber angle on the force at O1 and O2
根据减振器角度的增量调整后的结果可以得知,做负调整时,下铰接位置受力明显增加;正调整及倾角为0 处,上下位置处受力相较于基础结果均有一定幅度的增加.对于O1处的受力变化曲线,增量调整后虽在0~1.5 s 时段内的受力低峰值有所降低,但在2.0 s 左右的高峰值却均有上升,长期使用易导致减振器上下位置摆动的流畅性受到影响.
随后,基于上文对减振器安装角度的初步确定,开展对A~D四处铰接位置的受力影响分析,通过对双臂间距及长度增量调整,得到四位置处的受力变化结果,如图15.


图15 增量调整对A~D 点的受力影响Fig.15 The influence of incremental adjustment on the force on points A~D
图15(a)~图15(d)分别对应A~D四处铰接位置的受力随增量调整的变化情况.从中可以发现,增加双臂的长度可以有效降低四个位置的受力;减少臂间距虽可降低B,C两位置的受力,但对A,D两位置的受力起到副作用,并且降低的力远小于增加的力,故不考虑调整臂间距.增长双臂会导致车轮转弯时的灵活性受到影响,并且影响减振器的上下端受力情况,图16 为针对调整臂长,给减振器受力带来的影响结果.
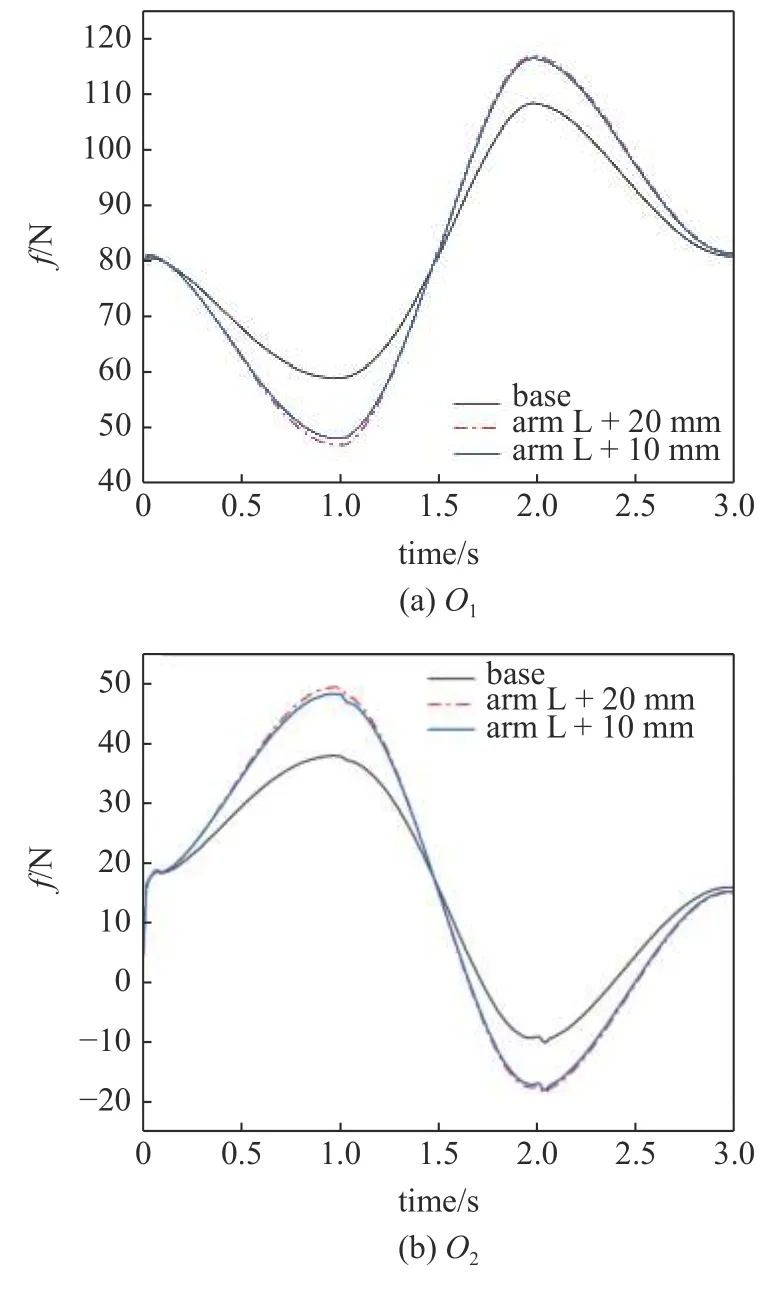
图16 臂长增量减振器受力影响Fig.16 The arm length incremental shock absorber is affected by the force
根据结果可以发现,增加臂长虽然能一定幅度的降低A~D四处位置受力,但会对减振器产生明显的附加垂向作用力,这不利于减振器的正常工作,长期使用会降低垂向调节行程.同时,在保证减振器倾斜角度的前提下,增加臂长意味着臂间距随之增加,故综合考虑,造成四处铰接位置受力受到影响.
纵臂式悬架的合理设计可以在提升垂向调节范围的同时,将轮胎侧向运动转变为纵向运动.即搭载此悬架的车辆,在底盘升降过程中,前后轴车轮产生纵向相对运动,从而缩短轴距,进一步减小转弯半径,提升机动灵活性.因此,悬架结构对车轮纵向移动量的影响作为重点研究对象,经过前期开展对减振器铰接位置,双纵臂间距、长度对车轮纵向位移的灵敏度分析,确定出主要影响因素为臂间距和臂长度两者,图17(a)为初步判断主要影响因素结果.
首先分别对臂间距以及臂长度进行增量调整,为了确保准确性,采用正负两方向对位置坐标进行改变.可以发现,0~1 s 减振器压缩过程中,车轮向整车质心方向发生位移,对臂间距做正增量及臂长度做负增量调整时,车轮位移均可达到50 mm 以上;1.5~2.5 s 底盘举升过程中,对臂长度及臂间距分别做负增量和正增量时,车轮位移在基础位置结果的上下5~10 mm 波动,基于此结果,结合考虑多变量的均一化调整影响整体准确定性,故对参数化变量进行交叉融合分析,得到图17(b)结果.

图17 参数增量对车轮纵向位移的影响Fig.17 The influence of parameter increment on the longitudinal displacement of the wheel energy
根据均一调整增量以及交叉融合两项迭代结果可以清晰发现,对纵臂间距和长度作出调整时,底盘降低和举升两个极限位置处,车轮发生的纵向位移均有所偏颇,易导致车轮做出不同程度的移动量、变形量,相比于添加量调整增量的结果,基础位置参数表现较为稳定,峰值相对均衡.
悬架作为缓解路面冲击的关键系统,通过导向机构来实现对外界力的传递、缓解,因此,在底盘升降过程中,车轮动能变化可以准确反应出悬架性能表现.首先分别通过对双臂间距及双臂长度进行正负增量调整,得到图18 所示结果.

图18 参数增量对车轮动能的影响Fig.18 The influence of parameter increment on wheel kinetic energy
通过动能变化曲线反应的结果,可以推断,臂间距及臂长度无论从均一调整增量或是进行交叉融合分析,都会导致车轮的动能变化出现波动,其中,调整双臂长度可以实现在0~1 s 和2~3 s 时段动能变化的相对平缓,但1~2 s 内,相较于基础位置结果,变化幅度略大,在实际应用过程中,车轮缓解冲击对整车的行驶平顺性起到决定性作用.
基于数据驱动模式,采用参数化设计,通过对增量的均一化、交叉化方式分别对车轮纵向位移以及车轮动能变化的影响因素进行综合比较,最终确定出悬架系统关键铰接的位置坐标.对于悬架系统性能优劣的判断,应结合悬架动挠度、悬架动载荷等进行综合判断.本文设计的悬架系统可有效解决车轮外倾的现象,同时对侧向位移进行消除,车轮在(-125 mm,125 mm)行程变化中的相关特性曲线如图19 .

图19 垂向行程中车轮特性曲线Fig.19 Wheel characteristic curve in the vertical process
为了确保垂向行程大幅提升的同时,轮胎上胎面与转向臂不会发生运动干涉,对此间距进行分析,可以发现,距离最近处为车轮动行程到最高点,此处的间距保证了撞击悬架限位概率为0.
分别进行轮胎外倾角、悬架动挠度以及车轮纵-垂-侧三向速度变化分析可以发现,悬架系统工作过程中,轮胎外倾角虽出现微量波动,但整体处于0 位,最大程度杜绝外倾现象;悬架动挠度应充足,避免颠簸路面带来的机构冲击;通过路面对车轮垂-纵-侧作用力随轮跳行程的变化情况可以发现,路面对轮胎侧向作用力为0,保证了车轮在工作过程中始终保持垂直于地面,轮胎接地面积实现最大化,车轮不存在横向运动激励.根据仿真结果可以得知,实现垂向行程的同时,降低车轮外倾的程度;将车轮纵向位移保持在相对合理的空间,提升车辆行驶性能,强化了悬架系统对缓解路面不平度带来的冲击能力,平缓的动能释放对行驶平顺性提供重要保障.
4.3 实物验证
为验证本研究悬架系统性能情况,基于上文开展的理论基础工作,搭建如图20 的一体化电动轮,为确保本研究可靠性,利用如图21 的全矢量线控平台进行实车验证.通过控制执行拨杆实现对空气弹簧内气体的充、放,以此达到底盘大行程升降性能要求,得到电动轮安装位置处车架高度变化情况.本研究主要针对车辆垂向动力学特性,忽略车辆左右两侧的差异性,故只针对单侧悬架系统进行动态测试,根据高度传感器测试信号反馈,得到如图22~图24 实验结果.

图20 一体化电动轮Fig.20 Integrated electric wheel

图21 全矢量线控平台Fig.21 Full vector X-by-wire control platform

图22 前轴升降Fig.22 Front axle lift

图23 车身单侧升降Fig.23 Single side lift

图24 底盘整体升降Fig.24 Overall lift of the chassis
通过对车辆左、右前悬架进行充、放气实验,得车架高度变化,结果可以发现:①举升过程中,车架高度变化平缓稳定,证明本研究对悬架开展工作的有效性;②前轴举升与下降过程中,左后轮位置处的高度未发生变化,表现出电动轮良好的独立性能.
作为高性能悬架系统,需具备单侧车身高度可调节功能,故对左侧前后两悬架系统进行充放气实验,可以发现:①左后轮在举升时首先介入对车架高度的变化影响,下降时对其影响迟后于左前轮对应位置处;②在同侧调节车身高度时,变化过程中相对可靠,高度稳定后产生微量波动,处在允许范围内,这是由于轮胎接地时地面产生法向作用力导致.
通过对所有悬架系统的升降触发,实现整车通过性能的进一步提升,得到如下实验结果,结合前面两组结论,可以发现:车架高度调节范围在220 mm附近,与初期测算理论范围(-125 mm~125 mm)相比较,较为合理,同时发现,左前轮在车身下降过程中的反应更为迅速,这是由于车身质心到前轴范围内重量偏大,同时也为后续开展车身姿态调节研究提供有效参考.
5 结论
本文面向全线控平台,结合多功能一体化电动轮结构特性,考虑全线控平台的应用场景,对主动悬架特性进行研究.基于数据驱动背景,开展悬架系统关键参数获取与辨识,提出一种双纵臂式主动悬架系统方案,可扩大垂向行程调节范围,为搭载此悬架系统的全线控底盘实现大行程升降奠定基础.
针对 7 DOF 整车动力学模型进行搭建,分析轮胎垂向运动与车身运动间的关系,结合导向机构力学分析,为悬架系统方案设计提供了理论依据.利用数据驱动方式,对悬架各项子系统进行特性测试与运动学分析,并据此精确推算出三项系统的关键数据.仿真测试与实车验证结果综合表明,本研究提出的悬架系统在车身高度调节过程中的作用呈现正向影响,满足高性能底盘的功能需求.本项研究同时为后续开展车身姿态调节稳定性控制工作奠定基础.
