基于流量与延误双层模型的交通信号优化研究*
2022-08-26王磊罗杰
王 磊 罗 杰
(南京邮电大学自动化学院、人工智能学院 南京 210046)
1 引言
现代社会,随着经济与城市化的高速发展,区域交通流不断增大,使得交通路网拥堵问题愈发严重[1]。现有的交通信号协调优化模型越来越难以解决交通拥堵问题,因此对于区域交通信号协调优化控制的研究也愈发受到重视。
J.Withanawasam 等[2]考虑相邻交叉口的交通密度差异,基于多智能体技术,建立了一种区域边界门控机制,实现宏观交通路网的动态协调控制;宋仲仲等[3]通过分析单点信号控制与区域信号相关理论,提出了采用区域协调控制方法来优化配时方案;G.B.Castro[4]提出一种基于生物激励神经网络的自适应交通信号控制算法,通过改变交通信号的周期和相位的顺序,提高了系统中的交通容量;Hongjun Xie等[5]根据实际区域路网的交叉口状况,采用过渡延误模型,定性分析禁左措施实施的可行性及影响,有效减少了区域交通流的平均延误;H.Cao 等[6]基于过渡延误模型,充分考虑区域内部交通流的动态特点,建立引入相位差的车辆平均延误模型,有效降低了区域延误。上述研究表明,大部分交通模型并未考虑到交叉口入口车道在不同相位情况下的排队车流与输出车流对区域路网延误的影响。因此,区域交通模型需要进一步研究与改进。
本文首先分别将区域内各交叉口入口车道排队流量与输出流量的计算方法分为红灯信号相位与绿灯信号相位两种情况进行分析推导,构建区域交叉口总输出流量模型。其次在文献[6]的基础上,进一步考虑各交叉口入口车道上的车辆排队长度,并结合所推导的输出流量,构建区域车辆平均延误模型。最后建立以各交叉口总输出流量最大与车辆平均延误最小为目标的区域交通双层规划模型,并采用GASA算法[7]求解模型。
2 区域交通双层规划模型
双层规划是一种系统优化方法,具有递接结构,包含上层与下层两种问题[8]。上下层都有属于自己的目标函数与约束条件。其中,上层模型的目标函数和约束条件在受制于决策变量的同时也依赖于下层模型变量和最优解,而下层模型的最优解也受制于上层决策变量。
2.1 区域交通路网
研究表明[9],为了能够对区域交通进行更协调合理的控制,应对区域路网中的“丁”字路口采用3相位控制模式,“十”字路口采用4相位控制模式。
2.2 区域约束条件分析
通常在区域交通协调控制中包括公共周期、绿信比、相位差三个基本控制参数[10]。
2.2.1 信号周期
周期时长通常用C 表示。在某一区域路网中,为使各交叉口间能够保持协调控制,应对各交叉口C的取值设置如下约束:
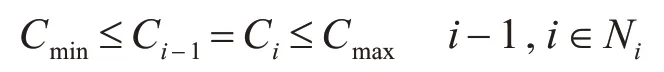
2.2.2 绿信比
绿信比通常用γ表示。在一个相位中为了能够有效协调周期中各相位中车流的通行,应对γ的取值设置上下限,且小于1,即:

2.2.3 相位差
相位差通常用θi,j表示。两相邻交叉口的相位差通常分为上行相位差θi-1,i与下行相位差θi,i-1,且可以相互转换。通常θi-1,i与θi,i-1应满足约束条件:

2.3 区域交叉口总输出流量
本文在对交叉口入口车道车流进行分析后,建立以区域内各交叉口输出车流量总和最大为目标函数的上层模型。
各交叉口入口车道的滞留排队车辆数主要受当前周期的配时参数、车流到达率以及该入口车道前一个相位结束后所滞留的排队车辆影响。图1中的(a)与(b)分别表示第i 交叉口第y 入口车道在不同条件下的车流到达情况,纵轴表示入口车道的车辆排队数,横轴表示第i 交叉口第y 入口车道在一个周期内的红绿灯分配时间;、为红灯时间与绿灯时间,Ci为周期时间;Si,y为交叉口i入口车道y的饱和流率。
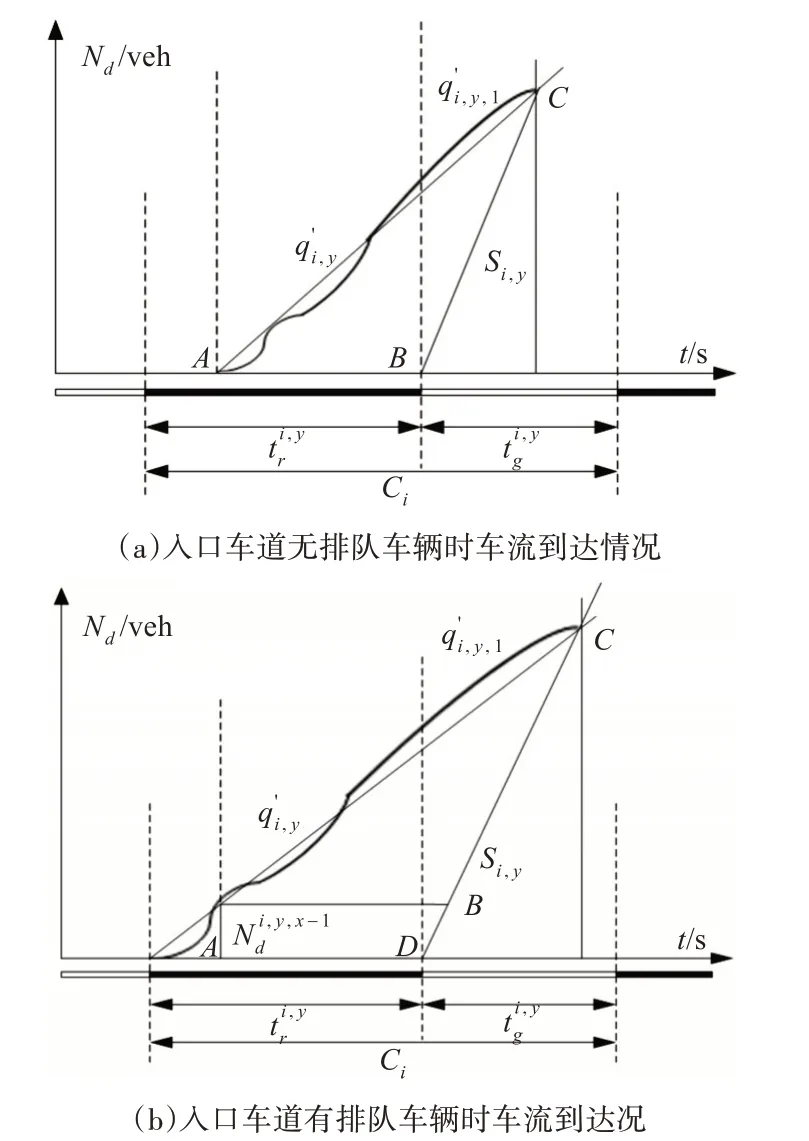
图1 区域路网简化图
其中,图1(a)表示交叉口入口车道无排队车辆时车流到达情况,点A 为车流到达交叉口入口停车线的时刻;点B 为排队车流头车启动时刻,即红灯结束时刻;点C 为累积的排队车流全部使出停车线时刻;为交叉口i 入口车道y 的车辆实际到达率。
图1(b)表示交叉口入口车道有排队车辆时车流到达情况[10],点O为交叉口前一个信号周期结束时刻;点A 为车流到达入口车道y 在前一周期所滞留的排队车辆尾部时刻;点D为交叉口入口道所有累积的排队车流头车启动时刻,及红灯结束时刻;点B为入口车道y在前一周期所滞留的排队车辆全部驶出停车线的时刻;点C 为累积的车辆全部驶出停车线时刻;为交叉口i 入口车道y 在相位x的前一相位结束时所滞留的排队车辆数;为交叉口i入口车道y的车辆实际到达率。
因此,根据图(a)与图(b),有如下分析:
定义wi,y为交叉口i 入口车道y 的饱和度,Ni为区域路网中的交叉口个数,i 为任一交叉口;Ni,y为交叉口i 的入口车道数,y 为任一入口车道;Ni,x为交叉口i的相位总数,x为任一相位;qi,y,x(c)为第i交叉口入口车道y在第c周期第x相位内所驶出的车流量;qi′,y为第i交叉口入口车道y的车辆平均到达率,通常为固定常量[10],其值为图(a)中线段AC与图(b)中线段OC 的斜率;Ndi,y,x(c)为第i 交叉口入口车道y 在第c 周期第x 相位结束时所累积的排队车辆数。
2.3.1 入口车道排队车辆数(c)的计算方法
当交叉口i 的某一信号周期开始运行时,其入口车道y 的排队车辆数为前一个信号周期最后一个相位结束时所滞留的车辆数,即:
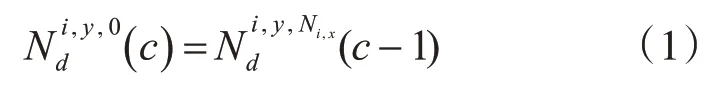
当信号周期运行至第x 相位时,有以下两种情况:
1)相位x在y车道上为红灯时
此时(c)为车道y上前一信号相位结束时的排队车辆数与红灯相位x 的时间内到达的车辆数之和,见式(2):
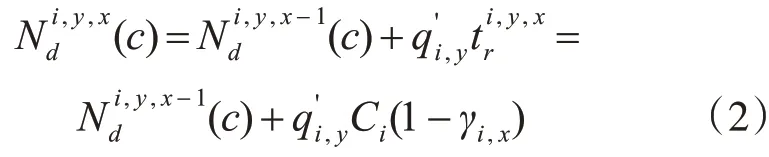
式中,(c)为交叉口i 入口车道y 在第c 周期第x 相位的前一相位结束时的排队车辆数,若无排队车辆或当车流驶向交叉口i 入口车道y 停车线时剩余排队车辆已消散完毕,则(c)为0;Ci为交叉口i 的周期时间,γi,x为交叉口i 相位x 的绿信比,Ci(1-γi,x)为车道y 在其红灯相位x 上的时间。
2)相位x在y车道上为绿灯时
当入口车道y 的绿灯相位x 开启时,该车道在红灯相位结束时所积累的排队车辆开始消散,若这些积累的排队车辆与上游交叉口驶入的车流在车道y 上处于非饱和或近饱和状态,即wi,y≤1,此时所有车辆能够以饱和流率Si,y在绿灯相位x的时间内全部驶出停车线,显然,此时的排队车辆(c)为0;而当车道y 上车流处于过饱和状态,
即wi,y>1,此时车流以饱和流率Si,y无法在时间内全部驶出,因此(c)的计算可见式(3):
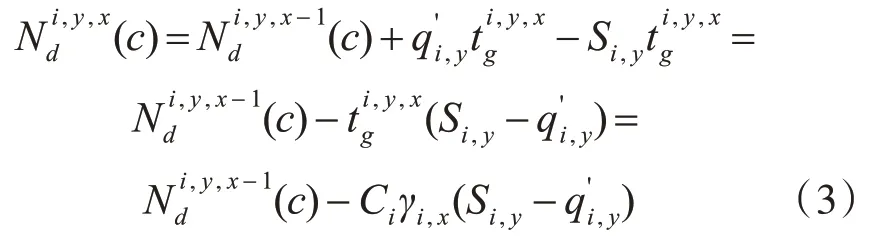
式中,为时间内车道y的到达车流量;为车道y 上的所有车辆在绿灯相位x 内以饱和流率Si,y所驶出的流量。所以,整理可得:

2.3.2 入口车道所驶出的车流量qi,y,x(c)的计算方法
1)相位x在y车道上为红灯时
显然,此时的qi,y,x(c)为0。
2)相位x在y车道上为绿灯时
当入口车道y 的绿灯相位x 开启时,该车道在红灯相位结束时所积累的排队车辆开始消散,于是:
当wi,y≤1 时,设t 为积累的排队车辆与上游交叉口汇入的车流的所有车辆全部驶出交叉口i停车线所需的时间,则此时qi,y,x(c)为t 时间内车道y 上的所有车辆以饱和流率Si,y所驶出的流量,即式(5):

因此可求得此时的qi,y,x(c)为

当wi,y≤1 时,很显然,此时的qi,y,x(c)为车道y上的所有车辆在整个绿灯相位x 的时间Ciγi,x内以饱和流率Si,y所驶出的流量,即式(7):

整理可得:

综上可得区域内各交叉口的总输出流量为

式中:Nc为观测周期个数;Ni为区域交叉口的数量;Ni,y为第i 交叉口的入口车道数;Ni,x为第i 交叉口在一个信号周期内的相位个数;qi,y,x(c)为第i交叉口入口车道y 在第c 周期第x 相位内所驶出的车流量。
2.4 区域车辆平均延误
针对车辆延误,R.M.Kimber 提出了过渡延误模型[11],与Webster稳态理论延误模型[12]相比,该延误模型能够适用于非饱和与过饱和两种状态,且能很好地描述近饱和状态下的交通状况。H.Cao等[6]在过渡延误模型的基础上,考虑了区域内部车流的动态属性,引入相位差,建立区域车辆平均延误模型。与过渡延误模型相比,该模型虽能降低车辆延误,却忽略了各交叉口入口车道上的车辆排队长度这一重要因素,导致计算结果存在较大误差。因此本文在此基础上结合所推导的输出流量,进一步建立考虑车辆排队长度的区域车辆平均延误模型。
2.4.1 区域外部延误
外部延误是指当车流通过外部入口车道进入该区域路网时,由于车流的随机性而造成的车辆延误,且入口车道也可能存在过饱和情况,因此对于外部延误可直接采用过渡延误模型进行计算[6],即式(10):

式中,d过渡延误公式。
2.4.2 区域内部延误
内部延误是指车流在内部交叉口入口车道上因排队而造成的延误。内部交叉口入口车流通常会在入口车道上形成车辆排队,需要分不同情况计算。
当车流自上游交叉口i-1 通过入口车道y 驶向交叉口i时,会造成以下几种延误:
1)车流通过入口车道y 驶至交叉口i 时遇到绿灯,即相位x在车道y上为绿灯,且在剩余的绿灯时间内全部通过,此时延误为0。
2)相位x 在车道y 上为绿灯,且车流并未全部在剩余的绿灯时间内通过,此时未通过的车辆会形成排队,造成部分车流受阻,从而产生延误。
3)相位x 在车道y 上为红灯,此时整个车流都会受阻,从而产生延误。
此外,由于车辆在行驶过程中会产生随机波动性,从而造成延误。于是,内部交叉口入口车道延误可分为部分车流受阻延误、整体车流受阻延误、随机到达延误,下面分别讨论。
1)部分车流受阻延误
当车流通过入口车道y 驶至交叉口i 遇到绿灯时,即相位x在车道y上为绿灯,车流的一部分会在绿灯结束前行驶出去,剩余部分会由于绿灯结束而受阻产生排队,这部分车流需要在交叉口i 入口车道y 的停车线上等待红灯时间结束才可离开。定义L 为交叉口i-1 与i 的间距,vˉ为车流平均速度,并设ta为受阻部分的车流从头车被红灯截停起到尾车到达受阻车辆排队尾部所经历的时间,则结合前文所介绍的相位差θi-1,i,有以下两种情况:
(1)交叉口i 入口车道y 上无排队车辆或剩余排队车辆全部驶出车道,则有:

图2 表示部分车流受阻的延误情况。在车道y上的绿灯相位x 结束时,受阻的车流中有辆车未能在绿灯相位内驶出,于是只能等待该车道上下一个绿灯相位。则在下个绿灯相位中剩余车辆需要以饱和流率Si,y并经历时间t才能全部驶出停车线,则有:

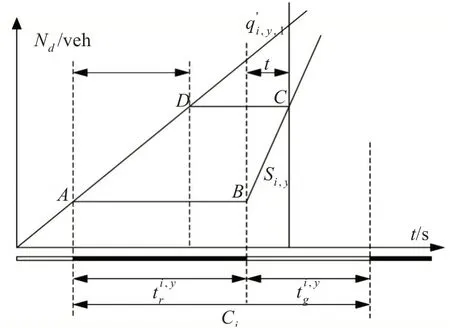
图2 部分车流受阻延误
则车道y上的部分受阻车流在该信号周期内的总延误Dpart1为⋈ABCD的面积[6],即:

(2)交叉口i 入口车道y 上存在正在消散的排队车辆,定义为车辆的平均长度,此处将前后车间距忽略不计,则结合式(3)易求得排队长度l 为,则有:

该情况下应确保正在消散的排队车辆不会对驶入的车流造成阻碍,定义ω为排队车辆消散波的速度[13],则易求得交叉口i 入口处正在消散的剩余排队车辆自头车消散至尾车所用时间β为,因此,其相位差应满足约束条件:

该情况下延误的计算依旧参照图2,结合式(13)与式(14)可得该情况下的总延误Dpart2为

2)整体车流受阻延误
当车流通过入口车道y 驶至交叉口i 时遇到红灯时,即相位x在车道y上为红灯,设tb为车流头车到达交叉口i 入口车道y 的停车线或排队车辆尾部起至红灯相位结束的时间,则:
(1)交叉口i 入口车道y 上无排队车辆或排队车辆已全部驶出车道,此时有如下公式:

图3表示车道y在该条件下整体车流受阻的延误情况。当车流在车道y 上行驶至停车线时,车道y上的相位为红灯,因而会造成车辆排队;当红灯相位结束时,绿灯亮起,累积的排队车辆需要以饱和流率Si,y并经历时间t 才能全部驶出停车线,且在这之后到达的车辆同样会以饱和流率Si,y在剩余的绿灯相位内驶出停车线,延误为0,则有:


图3 无排队车辆时整体车流受阻延误
则此时车道y 上的部分受阻车流在该信号周期内的总延误Dtotal1为ΔABC的面积[10],即:

(2)交叉口i 入口车道y 上有相位x 的前一相位所滞留的排队车辆,则结合式(2)或(3)易求得排队长度l为(c),则有:

图4为入口车道y该条件下整体车流受阻的延误情况。当车流在车道y 上行驶至排队车辆尾部时,车道y 上的相位为红灯,因而会造成车辆排队;当红灯相位结束时,绿灯亮起,累积的排队车辆需要以饱和流率Si,y并经历时间t才能全部驶出停车线,且在这之后到达的车辆同样会以饱和流率Si,y在剩余的绿灯相位内驶出车道y停车线,延误为0,则有:


图4 有排队车辆时整体车流受阻延误
此时车道y 上的部分受阻车流在该信号周期内的总延误Dtotal2为ΔOCD的面积,即:
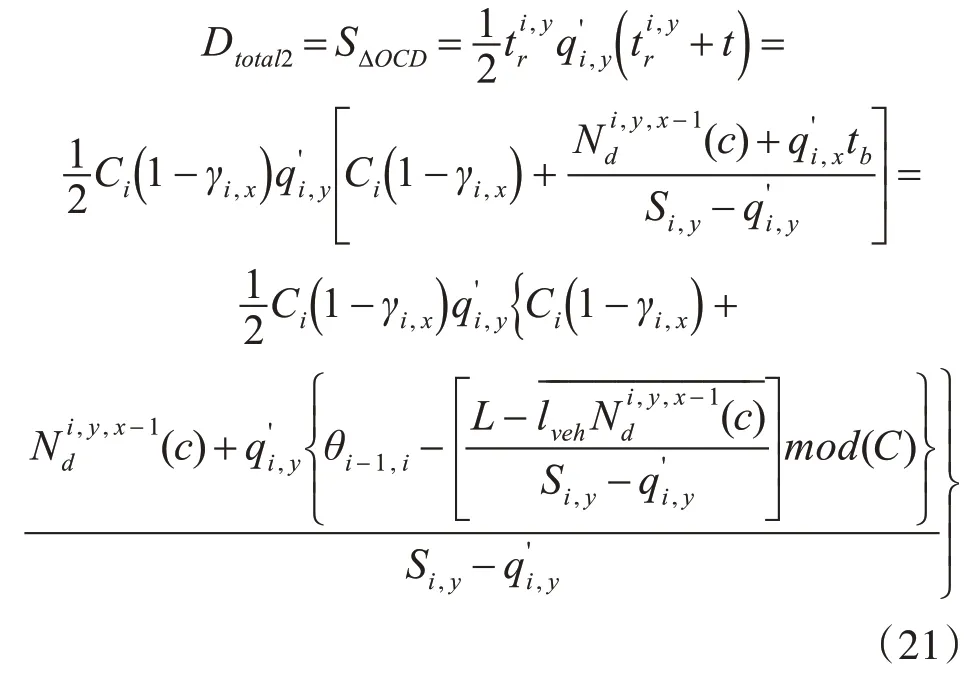
3)车流随机到达延误
上述研究均属于车流均匀到达延误,而忽略了车流随机到达延误。因此直接采用过渡随机延误公式进行计算[6],即:

式中,do为过渡随机延误。
综上可知,当车流以均匀车队到达时,会产生部分车流受阻延误与整体车流受阻延误,而这两种延误又分为无排队车辆与有排队车辆两种情况,则定义μ、α为

则区域内部交叉口i 入口车道y 上车流以均匀车队形式在一个周期内平均延误为
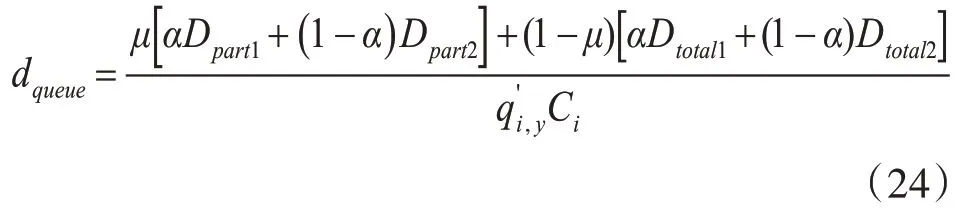
考虑到车流的随机延误,可得区域内部交叉口i入口车道y上车流平均延误为

2.4.3 区域内部延误
由以上对区域内部、外部各交叉口各入口车道在各观测周期内车流延误的研究,可得区域车辆平均延误计算公式如下:
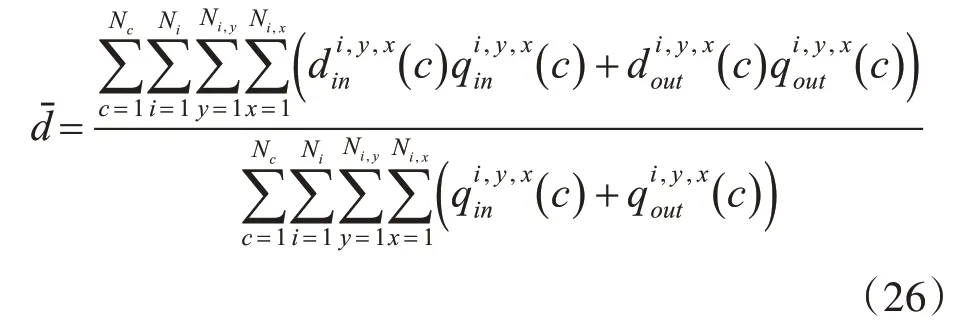
式中:Nc为观测周期个数;Ni为区域交叉口的数量;Ni,y为交叉口i的入口车道数量;Ni,x为交叉口i 在一个周期内的相位个数;(c)、(c)分别为区域内部、外部车流在交叉口i 入口车道y 在第c 周期第x 相位内的平均延误时间,分别由式(25)、式(10)得到,(c)、(c)分别为对应的排队车辆数,可由式(9)得到。
2.5 区域交通双层规划模型
综上可得到区域交通双层规划模型,如式(27)与式(28)所示。

式(27)与式(28)分别为上层与下层的数学模型,都包含各自的目标函数和约束条件。在上述两约束条件中,ti-1,i为车流从交叉口i-1 行驶至交叉口i 入口处正在消散的剩余排队车辆尾部所用时间;β为交叉口i 入口处正在消散的剩余排队车辆自头车消散至尾车所用时间。
3 基于遗传模拟退火算法的模型求解
3.1 遗传模拟退火算法
对于双层规划模型而言,无论其目标函数是否为凸规划,都存在Pareto最优解[8],因此本文采用智能算法求解模型。
遗传算法(Genetic Algorithm,GA)[14]是一种基于模拟生物遗传和进化过程的寻优算法,全局搜索能力较强,然而容易陷入局部最优解,局部搜索能力较差。模拟退火算法(Simulated Annealing,SA)[15]是一种基于Mente Carlo 迭代求解策略的寻优算法,该算法易跳出局部最优解,具有较强的局部寻优能力,然而其寻优过程较长。因此,针对这两种寻优算法各自的优缺点,刘伟铭等[7]提出遗传模拟退火混合算法(Genetic Algorithm for Simulated Annealing,GASA),该算法将GA与SA相结合,取长补短,增强了局部搜索能力,提升了寻优速度。
3.2 模型求解
结合GASA算法的一般步骤[7]对所提出的区域交通双层模型进行求解,具体求解流程如图5 所示。

图5 模型求解算法流程图
4 仿真实验
依据本文提出的区域交通双层规划模型,选取南京市栖霞区某区域路网中的部分交叉口与路段作为仿真实验对象,如图6(a)所示。针对不同的区域协调控制计算模型,分别求解三种不同模型的交叉口信号配时方案,并将不同方案的运行效果指标(即平均车辆延误与平均停车次数)进行对比。

图6 仿真实验所选取的区域路网图
由图6(b)所示,选取该路网中编号为1、2、5、6这4 个交叉口进行仿真。其中,交叉口2、6 为“十”字路口,均采用4相位配时;交叉口1、5为“丁”字路口,均采用3相位配时。
4.1 方案一
该方案采用H.Cao 等提出的未考虑车辆排队长度的单层区域车辆平均延误模型并基于GASA算法对区域路网进行协调优化。其优化所得的信号配时方案如表1所示。

表1 配时方案一
4.2 方案二
该方案采用本文提出的考虑车辆排队长度的单层区域车辆平均延误模型并基于GASA 算法对区域路网进行协调优化。其优化所得的信号配时方案如表2所示。

表2 配时方案二
4.3 方案三
该方案采用本文提出的区域交通双层规划模型并基于GASA 算法对区域路网进行协调优化。其优化所得的信号配时方案如表3所示。

表3 配时方案三
对上述三种配时方案以区域平均车辆延误与平均停车次数为效果指标进行评价。路网整体运行效果指标如表4所示。

表4 路网平均运行效果指标
由表4 可知,就平均车辆延误而言,方案二与方案一相比降低了12.97%,方案三与方案二、方案一相比分别降低了11.14%、22.67%;就平均停车次数而言,方案二与方案一相比降低了12.03%,方案三与方案二、方案一相比分别降低了10.26%、21.05%。因此,本文所建立的区域交通协调控制模型,能够有效降低区域平均延误时间和停车次数,表现出较好的优化效果。
5 结语
本文基于现有交通信号控制理论,通过分析区域在不同相位情况下的交通流特性与交叉口相关性,分别建立区域各交叉口总输出流量与公共周期的模型关系,区域车辆平均延误与绿信比、相位差的模型关系,并采用GASA 算法进行优化求解。实验表明,所提出的区域交通双层规划模型能够显著降低车辆平均延误与平均停车次数。
