粒子群模糊PID交叉耦合电机同步控制*

曹志强，王英志，胡 俊，刘 红

(长春理工大学光电工程学院，长春 130000)

0 引言

外鼓式直接制版机是一种由光学、电路以及机械系统构成的综合性、多学科的产品，各部分相对独立又协调统一工作。制版机工作时，在滚筒上雕刻的是由激光头的水平横向运动和滚筒的旋转运动合成的加工轨迹，要求采用两台电机同步协调地控制双轴完成制版任务。在激光扫描制版过程中会产生制版误差，通常对电机的速度进行控制，使双电机的速度匹配来消除制版误差，所以为了提高制版精度，降低各轴之间的同步误差成为了主要问题。通过对控制器发出的指令进行有效跟踪，来提高双电机之间的同步精度，实现对双电机的精确同步控制[1]。

双电机运动系统往往以轮廓误差作为评价同步控制性能的指标[2]。为了提高轮廓误差精度，加强电机间的同步性能，KOREN[3]提出了交叉耦合控制结构，建立了实时轮廓误差模型和误差补偿机制，通过补偿律反馈补偿到各轴中去，使轮廓误差实现闭环控制，从而提高轮廓精度。BARTON、LING等[4-5]提出将交叉耦合与迭代学习控制相结合的策略，以提高轮廓跟踪的同步性能。王炯宇、王丽梅等[6-7]采用一种模糊滑模控制器来解决滑模控制中的抖动现象，并以建立的轮廓误差模型的误差量作为控制器的输入，使误差量趋近于0，从而提高系统的轮廓精度。CHANG、刘洪珍等[8-9]提出一种基于神经网络的实时PID增益更新算法，能实时调整PID增益来提高加工质量和效率，降低轮廓误差。该算法可以利用单个神经网络来更新多轴系统的增益，所需的计算负荷显著降低。

由于在模糊PID控制器中，控制效果因量化因子和比例因子的不同取值而产生影响。通常情况下，利用人工经验对量化因子和比例因子进行选择，可能无法获得最佳值[10]。本文设计了基于PSO的模糊PID控制器，通过PSO优化模糊PID控制器中的量化因子和比例因子，实现对模糊控制器中参数的最佳调整，让PID参数进行实时动态调整，缩短轮廓误差补偿时间。再将基于PSO的模糊PID控制器与交叉耦合控制器结合，减小了系统的轮廓误差。利用MATLAB平台对双电机同步性能进行了仿真，对控制算法进行了验证。

1 电机模型与误差分析

1.1 永磁同步电机模型

在旋转坐标系下，永磁同步电机的数学模型可以表示为[11]：

(1)

磁链方程为：

(2)

式中，ud、uq、id、iq、Ld、Lq分别是直、交轴的电压、电流和电感；ψd、ψf为直、交轴磁链；ψf为定子磁刚在电枢中耦合磁链；R为动子相电阻；ωr为转子电角速度(ωr=π/τv)；v为电机运行速度；τ为极距。

永磁同步电机的机械运动方程为：

(3)

式中，M为电机动子质量；B为粘滞摩擦系数；F为摩擦力、负载阻力及端部效应引起的推力波动等扰动；Km为常值比例系数。

对式(3)做拉普拉斯变换得永磁同步电机从电流到机械转速的传递函数为：

(4)

1.2 系统轮廓误差分析

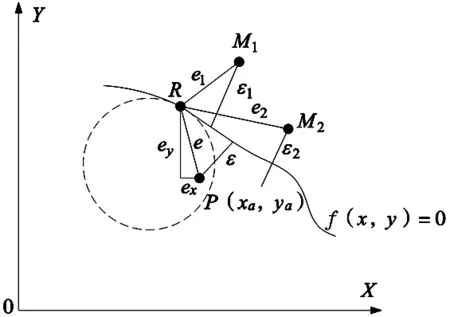
图1 轮廓误差模型

双电机协调运动控制系统中，存在两种误差：轮廓误差和跟踪误差。跟踪误差是指当前的理论指令位置与实际响应位置之间的误差。而轮廓误差是指在某一时刻双电机带动双轴协调运行的理论指令轨迹与实际响应轨迹之间的最短距离，又叫合成误差[12]。当期望规划曲线是圆弧路径时，建立的圆弧轮廓误差模型如图1所示。

图1中，R为给定的理论指令位置，P(xa,ya)为系统实际响应位置，由图1可知，ε为轮廓误差，e为跟踪误差，ex、ey分别是跟踪误差沿X、Y轴的分量。当两个电机一起工作时，仅提高单个电机所控制轴的跟踪精度不能有效解决轮廓精度的问题。在图1中，比较两个点M1和M2表明在M1点处的跟踪误差很小，但是在点M1处的轮廓误差ε1大于在点M2处点轮廓误差ε2。

设曲线方程为f(x,y)=0，图1中系统轮廓误差可表示为：

(5)

式中，O(xo,yo)为理论指令位置R点的内接圆心坐标；ρ为R点的内接圆半径。

(6)

式中，α是轨迹的切线与理论指令位置处的水平轴之间的角度。

将式(5)用泰勒级数展开，并忽略展开式高次项，得到轮廓误差公式：

(7)

根据以上分析，轮廓误差模型可以描述如下：

ε0=excx+eycy

(8)

式中，cx和cy为交叉耦合增益系数。

2 控制器设计

2.1 模糊PID控制器简介

本文依据双电机同步控制系统的控制功能要求，设计了模糊PID控制器，其基本控制结构和工作原理如图2所示。

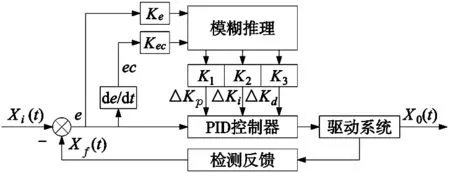
图2 模糊PID控制结构图

由图2可知，模糊PID控制器由模糊推理控制与PID控制器构成，模糊控制器的输入为电机运行过程中产生的跟踪误差e和误差变化率ec，输出为ΔKp、ΔKi、ΔKd，其中Ke、Kec为量化因子，K1、K2、K3为比例因子。然后将模糊推理后生成的输出变量导入到PID控制器中，经过PID控制器对参数整定后输入到系统，从而进行控制。

由于被控对象实际要求的变化范围不能由输入变量直接得到，需将输入变量乘以量化因子，使输入变量从基本论域转换到相应模糊集的论域。量化因子的不同取值可以影响基本论域不同程度的缩放，从而影响误差控制的灵敏度。比例因子具有相同的特性。

对于不同的e和ec，PID参数依据模糊规则进行调整，以满足控制要求。PID自整定参数按式(9)进行计算：

(9)

式中，Kp0、Ki0、Kd0为PID参数的初始值；ΔKp、ΔKi、ΔKd为模糊控制的输出；Kp、Ki、Kd为最终控制输出参数值。

在MATLAB中建立模糊控制器，设定输入变量e、ec和输出变量ΔKp、ΔKi、ΔKd的模糊子集均为{负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)}。e和ec的模糊论域均为(-6,6)，ΔKp、ΔKi、ΔKd的模糊论域分别为(-3,3)、(-0.6,0.6)、(-3,3)。根据隶属度函数特性及其系统特性要求，用灵敏度较强的三角形隶属度函数表示中间部分，用Z型隶属度函数表示负边界部分，用S型隶属度函数表示正边界部分。

根据PID控制调节经验，设计模糊控制规则，共制定出49条规则，针对ΔKp、ΔKi、ΔKd3个参数来分别进行整定，模糊规则表如表1所示。

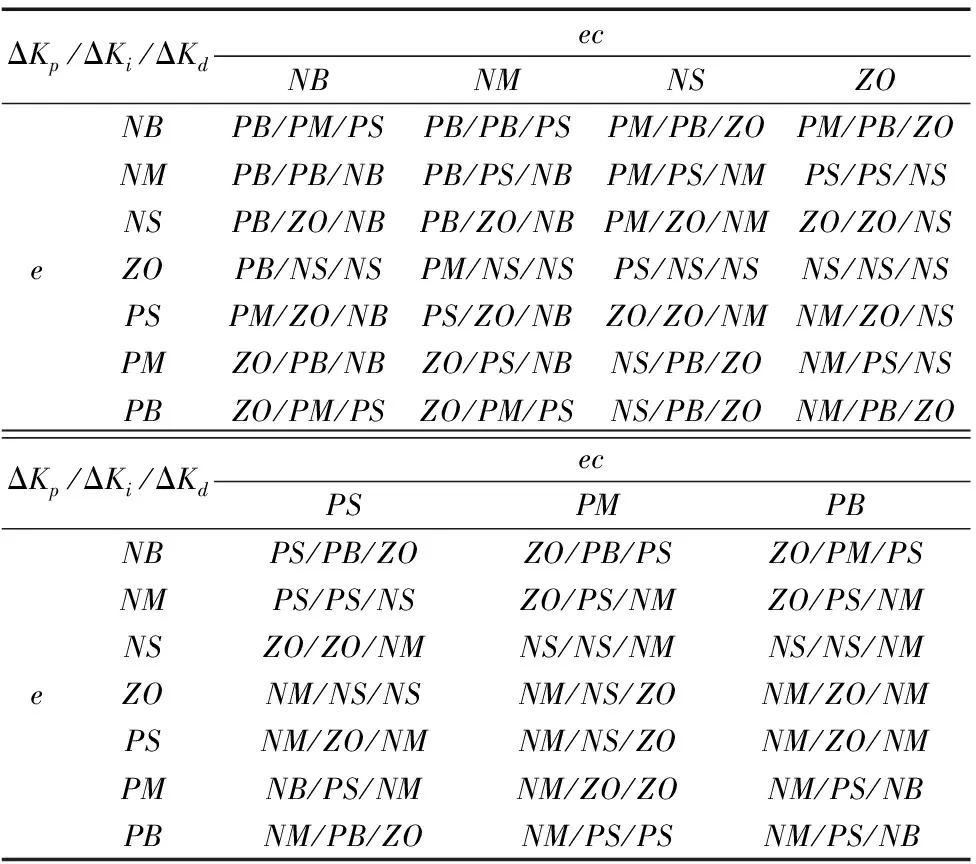
表1 模糊规则表

模糊控制存在自适应能力有限以及精度不高等问题，此外模糊PID控制器中的量化因子和比例因子，通常需要根据人工经验耗费大量时间反复调整它们的取值，随机性大，而且无法确定最佳的控制器参数。在这种情况下，为了优化模糊控制器中的量化因子和比例因子，引入粒子群算法，实现对模糊控制器中参数的最佳调整，从而实现更理想的控制效果。

2.2 粒子群模糊PID控制器设计

粒子群算法是一种受鸟群行为启发的全局优化算法。每个粒子代表一个可能的解向量，通过跟踪个体最优解与全局最优解以更新速度和位置来实现全局优化[13]。粒子在空间中的相应位置和速度可以表示为：

(10)

(11)

(12)

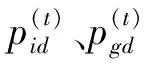
PSO优化模糊PID控制器参数的流程如图3所示。

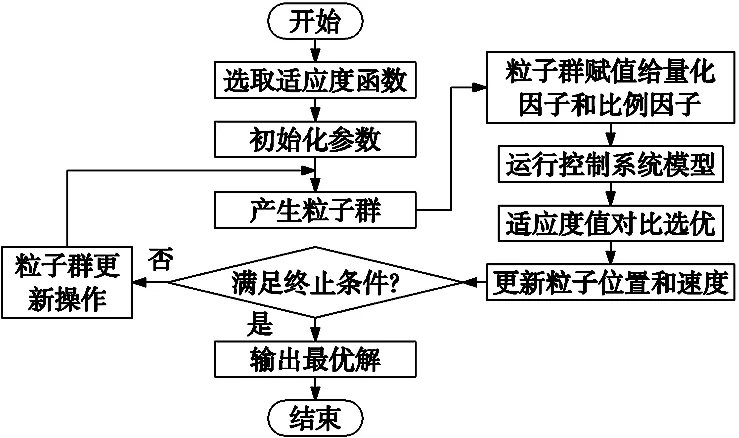
图3 PSO优化模糊PID参数的基本流程

适应度反映了PSO优化过程中最优值的优良程度，直接影响PSO的性能。时间乘误差绝对值的积分准则(ITAE)能够反映控制系统的速度和精度，根据该准则设计的控制系统响应速度快，超调量小。因此，本文选用ITAE为目标函数，具体公式如式(13)所示：

(13)

式中，t为时间；e为误差。

2.3 粒子群模糊PID交叉耦合控制器设计

传统的交叉耦合模型分别由系统轮廓误差的实时计算与分配补偿构成。在实际加工制造过程中，该方法可以有效解决双电机联动产生的各电机动态性能不匹配的问题[14]。但仅仅依靠交叉耦合控制仍然不足，例如，对轮廓误差的建模和分析表明，在X-Y平面上加工平面自由曲线和圆弧轨迹时，轮廓误差将随轨迹曲线位置点的变化而改变。本文将交叉耦合算法与粒子群模糊PID控制相结合，设计了一种双电机同步协调控制系统，控制结构模型如图4所示。

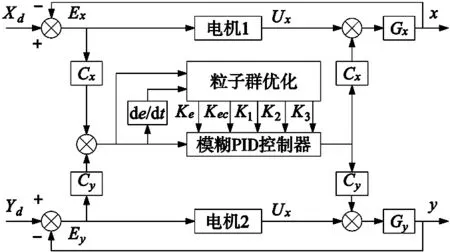
图4 粒子群模糊PID交叉耦合控制模型

图中，Xd、Yd表示输入信号，x、y表示输出信号，Ex、Ey表示电机1、2的跟踪误差，Gx、Gy表示电机1、2的传递函数，Cx、Cy表示关于电机的交叉耦合增益。粒子群模糊PID交叉耦合控制器可以通过电机控制运动轴得到反馈信息，为了寻求反馈到各电机的最佳补偿律，对轮廓误差模型增益进行实时修正，从而可以及时补偿轮廓误差。

3 仿真结果与分析

3.1 粒子群模糊PID参数优化仿真

为验证粒子群模糊PID控制的性能，利用MATLAB对模糊控制器参数进行寻优，粒子群算法的各项参数设置为：惯性权重ω=0.6，学习因子c1=1.414，c2=1.632，维数D=5，粒子群规模为100，最大迭代次数为100，最小适应度值为0.01，经过算法优化选取后得到最优的量化因子与比例因子，然后将寻优后的参数导入到Simulink中，调整模糊控制器论域。

在Simulink内建立模糊PID控制器与粒子群模糊PID控制器的仿真平台，通过输入相同的原始信号来仿真对比两种控制器的优劣，初始PID控制器参数设定为Kp=2、Ki=1、Kd=2，采用ITAE为指标，量化因子、比例因子和适应度值的优化结果如图5～图7所示。

图5 量化因子优化结果 图6 比例因子优化结果

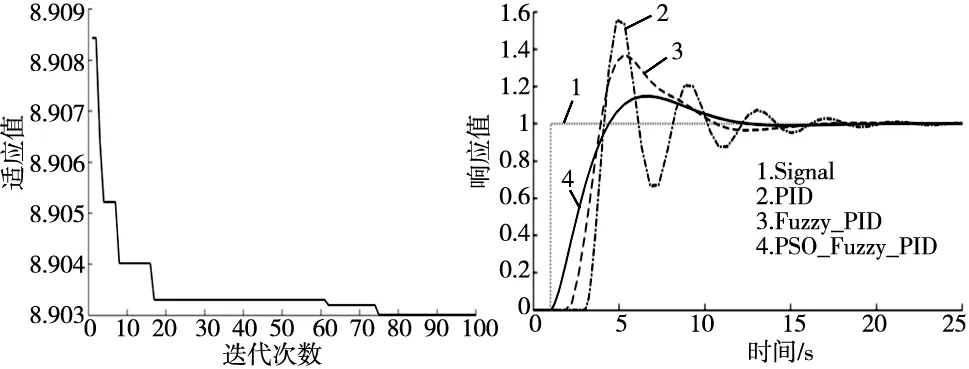
图7 适应度值优化结果 图8 不同控制器的响应曲线

由图5～图7可以看出，粒子群优化后得到的参数为：Ke=2.449，Kec=1.645，K1=11.567，K2=11.751，K3=5.561，当迭代次数达到17次左右时，适应度值趋于稳定，取得最优适应度值J=8.903。

图8为PID、模糊PID与粒子群模糊PID控制方法在相同输入信号条件下，所对应的响应曲线。在PID控制下，系统的超调量大，最大响应值达到1.58，响应速度慢，达到3.1 s，响应值才开始变化，调节时间长，24 s以后响应值趋于稳定；在PID控制下增加模糊算法模块，降低了系统的超调量，最大响应值为1.36，提升了系统的响应速度，1.9 s后响应值开始变化，调节时间缩短，20 s后响应值趋于稳定，但从响应曲线可以看出依旧存在不足；而粒子群模糊PID控制进一步降低了系统的超调量，最大响应值仅为1.15，并且响应速度快，1 s后响应值就开始变化，达到稳定时间较短仅需17 s。粒子群算法依据性能指标，对模糊PID控制器中量化因子Ke、Kec与比例因子K1、K2、K3寻优整定，调整模糊控制器的论域，提升了PID控制器的性能。

3.2 粒子群模糊PID交叉耦合控制算法仿真

为验证粒子群模糊PID交叉耦合算法的有效性，在MATLAB/Simulink环境下对双电机协调运动控制系统进行圆弧轮廓控制仿真实验，采用两台参数相同的永磁同步电机作为驱动部件，电机参数为：M=25.0 kg，B=0.2 N·s/m，Km=25 N/A。所选跟踪轨迹分别为x(t)=sin(πt) mm，y(t)=cos(πt) mm，仿真结果如图9～图11所示。

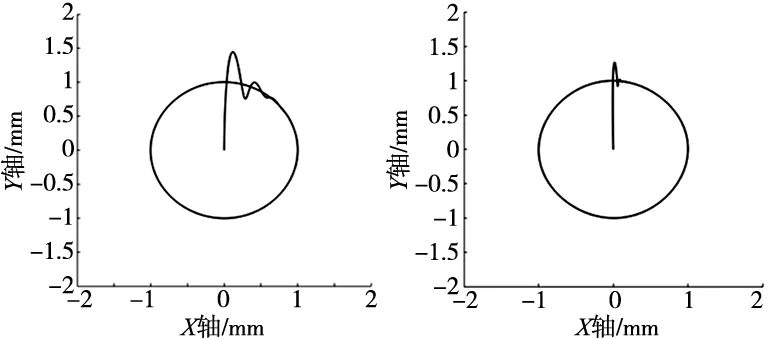
(a) 模糊PID交叉耦合跟踪轨迹 (b) 粒子群模糊PID交叉耦合跟踪轨迹

(a) X轴位置误差

(b) Y轴位置误差

由图9、图10可知，粒子群模糊PID交叉耦合控制能更好的跟踪所选的圆形轨迹，对比位置跟踪误差曲线可以看出，在模糊PID交叉耦合控制下达到稳态后的X轴位置误差约为-0.024～0.024 mm之间，Y轴位置误差约为-0.027～0.028 mm之间，而在粒子群模糊PID交叉耦合控制下达到稳态后的X轴位置误差约为-0.01～0.01 mm之间，Y轴位置误差约为-0.009～0.029 mm之间，明显减小了位置跟踪误差。

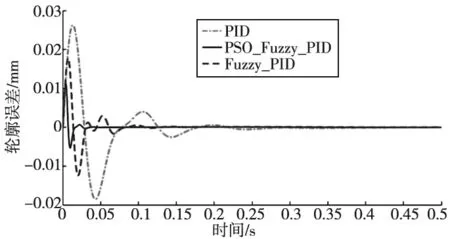
图11 不同控制方法的轮廓误差输出曲线

从图11可以看出，3种不同的控制方法对轮廓误差的控制效果，由好到差的顺序依次为粒子群模糊PID交叉耦合、模糊PID交叉耦合、PID交叉耦合，轮廓误差值如表2所示。

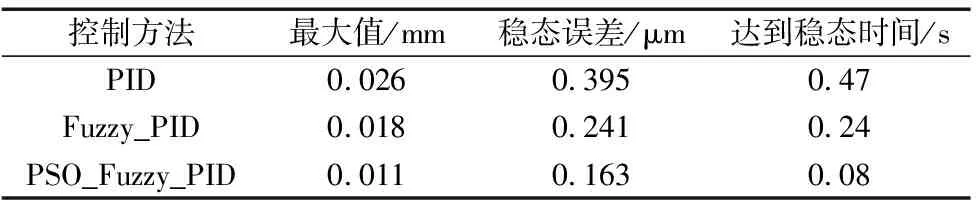
表2 轮廓误差

由表2可得，采用PID交叉耦合控制时，系统轮廓误差回复时间长，达到稳态所需时间为0.47 s，快速性差，最大轮廓误差值达到0.026 mm，误差达到稳态后的值为0.395 μm；采用模糊PID交叉耦合控制时，系统轮廓误差回复时间缩短，但依旧较长，达到稳态需要0.24 s，最大轮廓误差有所降低，为0.018 mm，误差达到稳态后为0.241 μm；而采用粒子群模糊PID交叉耦合控制后，系统轮廓误差能快速达到稳态，仅需0.08 s，调节时间短，且最大轮廓误差仅为0.011 mm，达到稳态后轮廓误差为0.163 μm，相比较模糊PID交叉耦合控制和PID交叉耦合控制，最大轮廓误差分别降低了38%、57%，达到稳态后的轮廓误差分别降低了32%、58%，响应速度分别提升了66%、82%。

为了进一步验证粒子群模糊PID交叉耦合算法的有效性，在相同仿真条件下，首先改变轨迹幅值，将上述所选跟踪轨迹的幅值增大为原来的2倍进行仿真，即：x(t)=2sin(πt) mm，y(t)=2cos(πt) mm；再改变跟踪轨迹，将跟踪轨迹选为椭圆曲线进行仿真，即：x(t)=2sin(πt) mm，y(t)=cos(πt) mm，轮廓误差仿真结果如图12所示。

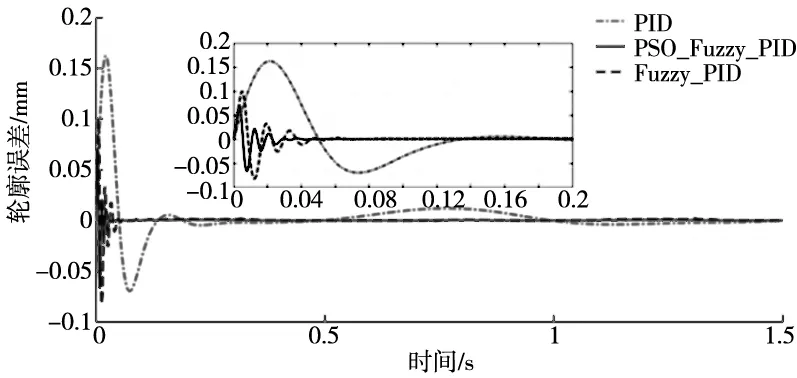
(a) 幅值增大2倍的圆

(b) 椭圆

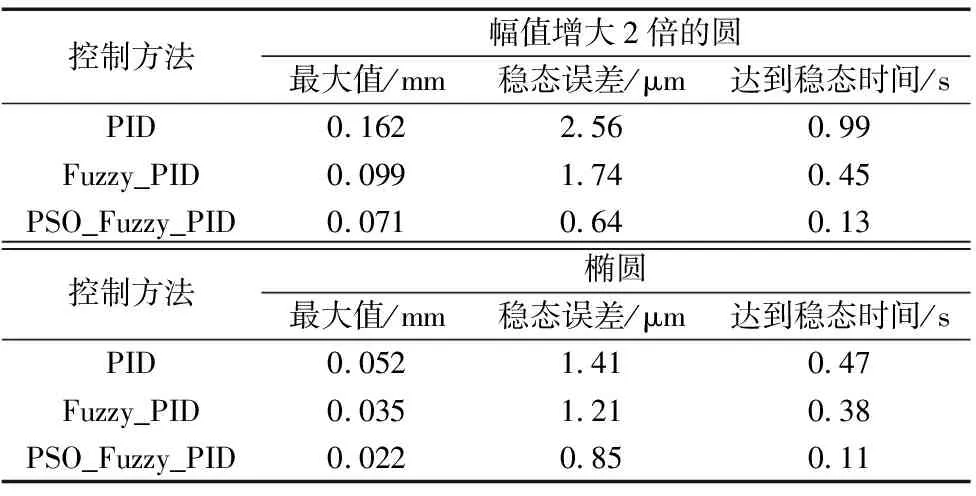
表3 不同跟踪轨迹的轮廓误差

由图12和表3看出，当跟踪轨迹为幅值增大2倍的圆和所设椭圆时，粒子群模糊PID交叉耦合控制比模糊PID交叉耦合控制产生的最大轮廓误差分别降低了28%、37%，达到稳态后的轮廓误差分别降低了63%、29%，响应速度分别提升了71%、71%。相比PID交叉耦合控制时，产生的最大轮廓误差分别降低了56%、57%，达到稳态后的轮廓误差分别降低了75%、39%，响应速度分别提升了86%、76%。

从上述分析可以得知，当改变幅值即从单位圆变为幅值增大2倍的圆时，本文算法更大程度地降低了轮廓误差的范围，响应速度也有少量的提升；当改变轨迹即从单位圆变为所设椭圆时，降低的轮廓误差范围相近，但响应速度提升明显。

因此，在对不同幅值与不同轨迹的跟踪控制下，粒子群模糊PID交叉耦合算法都能快速达到轮廓误差的稳态，调节时间短，响应速度快，且轮廓误差的范围小，从而显示出本文算法的优越性。

根据上述仿真结果可知，将粒子群模糊PID算法模块添加到交叉耦合控制器中，通过实时调整PID参数，可以有效地减小由于在实际的运行环境中电机速度和运动不匹配而引起的轮廓误差，提高电机间协调控制的性能。同时，系统可以更加精确的跟踪预期参考轨迹，减小了位置跟踪误差，且缩短了反应时间，轮廓轨迹的响应速度得到提高。

4 结论

为了减小双电机之间协调或同步运动带来的轮廓误差，提高双电机同步控制精度，提出了一种粒子群模糊PID控制与交叉耦合控制相结合的控制方法。通过PSO优化量化因子与比例因子，模糊控制器中的参数达到最佳调整，从而实时整定PID控制器参数，以适应被控系统的动态变化。再结合交叉耦合控制，改变幅值和轨迹分别进行跟踪仿真，对比分析后发现，粒子群模糊PID交叉耦合控制在不同条件下，均能减小系统的轮廓误差，缩短轮廓误差补偿时间，并达到最优；其次，此控制算法更有效的提高了双电机系统的运动精度，从而提高了制版系统的同步控制性能。