基于ELM-ARX组合模型的预测控制算法研究及应用

陈 颖 赵朋程 贾红霞 杨 丽 马 健

石家庄学院机电学院 河北石家庄 050035

实际工业控制系统中，许多控制对象都是多变量系统，具有非线性、时滞性和不确定性。多数的控制算法对模型精度具有较大的依赖性，建模技术在现代的工业生产中起着极其重要的作用。另外，工业流程控制过程中存在许多不确定性干扰因素，导致控制算法的控制精度较低。

经过众多学者的改进研究，模型预测控制(Model Predictive Control，MPC)[1]技术对实际工业过程控制产生了巨大影响，并且已经在工业过程多个领域中获得了成功应用，如网络化多智能体[2]、永磁同步机[3]、硅单晶直径生成控制[4]、直升机轨迹跟踪控制[5]等。在模型预测控制算法研究中，建立控制系统的预测模型精度决定了后续预测控制的效果。因此，相关学者采用组合模型建模的思想建立被控系统的模型，进而实现预测控制的研究。如Chen等[6]提出了一种自适应多层非线性组合模型预测控制算法，并将其应用于水泥熟料烧成过程篦冷机系统的控制仿真中；Yin等[7]将连续搅拌釜反应器作为被控对象，提出了一种基于映射数值组合模型的预测控制算法；Xiao等[8]结合多目标蝙蝠优化算法构建了组合预测模型，并在风电预测中实验应用；杨剑锋等[9]提出一种自适应并联组合模型预测控制算法，在化工酸碱中和反应过程中进行了仿真实验；郝晓辰等[10]提出了一种BP-ARX组合模型预测控制算法，并成功应用于水泥分解炉温度多变量控制中。

Huang等提出了极限学习机(Extreme Learning Machine，ELM)建模方法[11-12]，ELM是一种单隐含层前馈神经网络，训练速度快，有优良的泛化性能，避免了如BP神经网络容易陷入局部最小值、训练速度缓慢等问题，在各个领域得到了广泛应用。如数据函数辨识[13]、光伏发电量预测模型[14]、齿轮故障诊断[15]、太阳辐射率模型[16]、自适应控制模型[17]等。因此，将ELM应用到预测控制系统建模中是可行的。

因此，本文首先采用ELM算法建立控制系统的稳态非线性模型，利用具有外界输入的自回归算法(Auto Regressive with eXogenous inputs，ARX)[18]建立控制系统的动态线性模型，构建控制系统的ELM-ARX组合模型；其次，推导预测步数内控制系统的被控变量预测输出值，提出基于ELM-ARX组合模型的预测控制算法；最后，通过Matlab数据仿真实验以及水箱控制应用实验，验证提出的预测控制算法有效性和可行性。

1 ELM-ARX组合模型建立

1.1 ELM稳态非线性模型

极限学习机通过对输入层到隐含层权重与隐含层的阈值的随机赋值，将单隐含层前馈神经网络的参数训练转化为求解线型方程组。根据Moore-Penrose广义逆求解的到方程组的最小范数最小二乘解作为隐含层到输出层的权重，即完成了极限学习机的训练。极限学习机网络结构如图1所示。

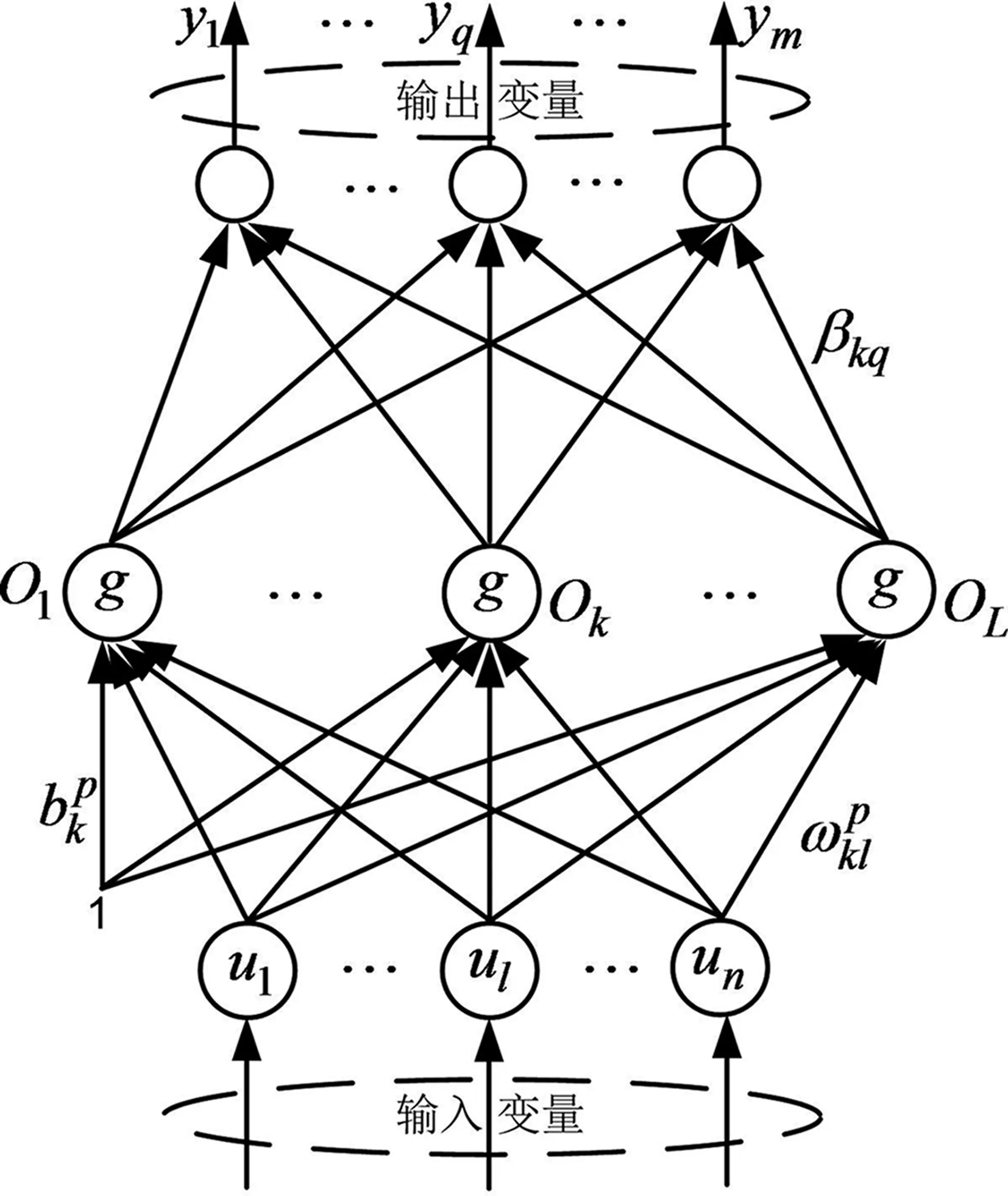
图1 极限学习机网络结构图Fig.1 Network structure diagram of Extreme Learning Machine

(1)

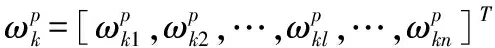
控制系统非线性稳态模型可表达为如式(2)所示的矩阵形式：

Y=Hβ

(2)

式中，隐层输出矩阵H=[hkj]，hkj=g(ωkuj+bk)，输出层权值矩阵β=[β1，β2，…βk，…，βm]T，输出矩阵Y=[y1，y2，…yj，…，yN]T。

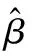
(3)

式中，H+为隐层输出矩阵H的摩尔彭德罗斯广义逆。

1.2 ARX动态线性模型

ARX模型是一种黑箱模型，由操作变量、被控变量和系统噪声干扰量组成的，能表示系统特性的线性数学模型，利用最小二乘法即可直接获得控制系统的动态线性模型。

设被控系统的动态线性特性可用如下ARX模型来近似描述：

A(q)y(k)=B(q)u(k)+e(k)

(4)

式中，A(q)=1+a1q-1+…+anq-n，B(q)=b1q-1+b2q-2+…+bmq-m，q-1为后移算子，e(k)是白噪声。

用获得的nu个输入的伪随机二进制(PRBS)信号激励系统，测得对应的ny个输出变量的值，用最小二乘法辨识得到如下描述系统增量关系的2阶ARX动态线性模型：

Δy(k)=A1Δy(k-1)+A2Δy(k-2)+B1Δu(k-1)+B2Δu(k-2)

(5)

式中，A1、A2、B1、B2为动态模型参数，A1，A2∈Rny×ny，B1，，B2∈Rny×nu；Δy(k)=y(k)-ys(k)，Δu(k)=u(k)-us(k)；ys(k)，us(k)分别是系统稳态输出输入。

1.3 组合模型建立

用线性ARX模型来描述非线性控制系统的动态特性，用伪随机二进制信号来测试控制对象。令:

A0=I-A1-A2

(6)

则控制系统动态线性模型的稳态增益矩阵K∈Rny×nu可表示为：

(7)

式(7)的稳态增益就是ARX模型的动态增益。保持A1、A2不变，令:

(8)

将式(8)代入式(5)，控制系统的非线性特性可描述为：

(9)

可求得输入变量ui(k)对应于输出变量yj(k)的动态增益为：

(10)

由此，可求得任意输入u(k)所对应的动态增益矩阵Ks。对于非线性控制系统来说，用当前时刻的实际输出值所对应的动态增益Kc和下一个输出设定值所对应的动态增益Kn的线性外推插值来表示未来预测时域内的实际动态增益，将会具有较高的预测精度。所以在未来预测时域内的输入u(k+p)所对应的动态增益，可用下式表示：

(11)

式中，Kn、Kc分别是稳态输入向量us(k)，us(k+1)对应的动态增益矩阵。

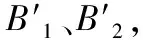
(12)

综上所述，建立的ELM-ARX组合模型结构如图2所示。通过系统实际的动态增益将系统的ELM稳态模型和ARX动态模型有机地结合在一起，推导出了包含系统稳态特性和动态特性的ELM-ARX组合模型，该组合模型可以完全反映出控制系统的特性。

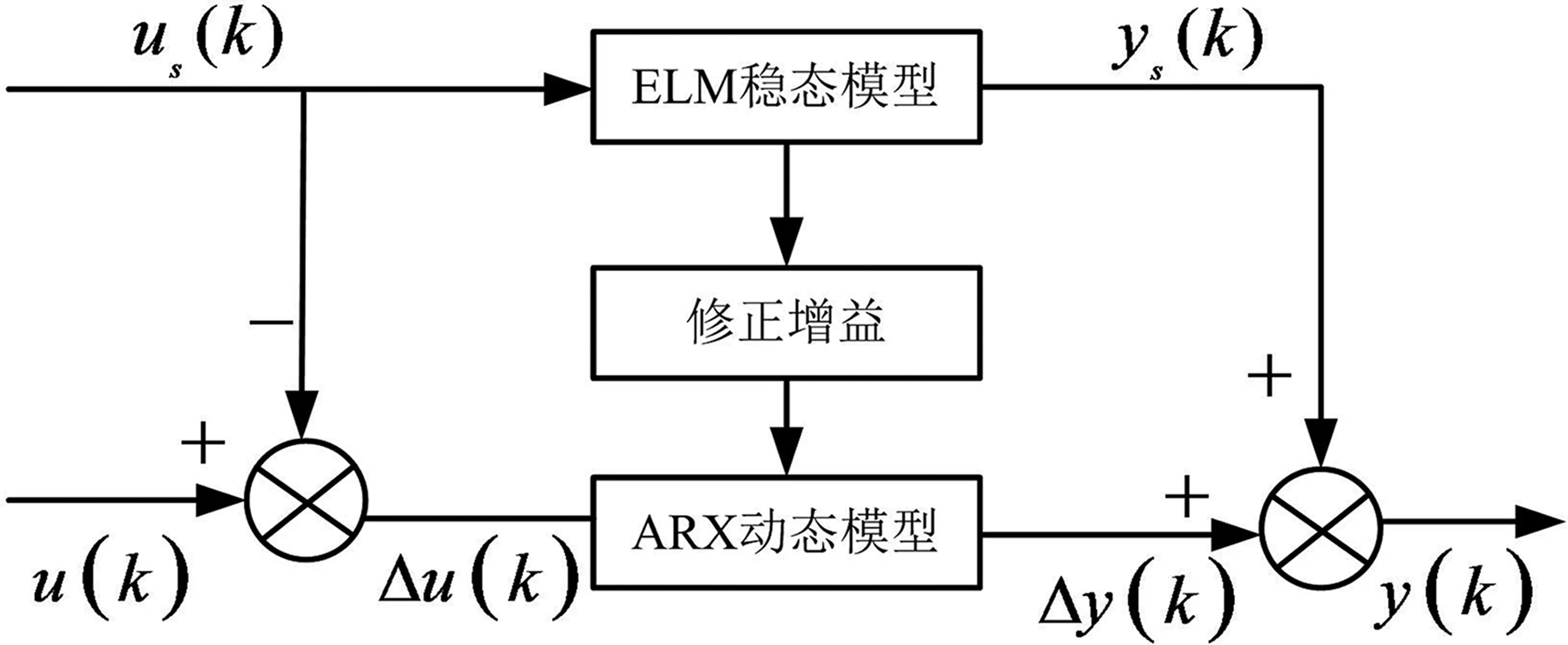
图2 ELM-ARX组合模型结构图Fig.2 Structure diagram of ELM-ARX combined model

2 基于ELM-ARX组合模型的预测控制算法研究

2.1 输出预测

取预测时域为P，控制时域为M(且P≥M)，推导ELM-ARX组合模型的输出预测值计算表达式。为使模型输出与实际输出数据的误差最小，即按式(13)求取一组适当的模型参数使得取得最小值。

(13)

对式(13)求导，即可求得模型的最优辨识参数A1、A2、B1、B2。令:

(14)

式中，n=2，3，…，P+1，S∈Rny×ny，T∈Rny×nu，Tg∈Rny×nu。

写成矢量形式，多步输出预测增量值的表示式为：

G22Δu2(k-1)+F1Δy(k)+F2Δy(k-1)

(15)

根据式(19)求得的未来预测时域内输出增量值，预测输出经位移矩阵进行转换，从而可得到预测输出：

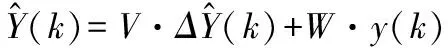
(16)

2.2 滚动修正

为了消除诸多因素引起的预测值的误差，采用滚动误差修正法对其修正，利用k时刻的预测误差：

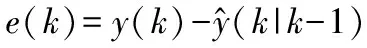
(17)

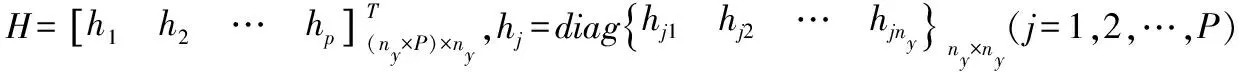
(18)

取参考轨迹为：

(19)

则控制系统带约束的最优化目标函数及其约束条件可表示如下式所示：

(20)

式中，Q=qI、R=rI分别是输出误差和控制增量的加权矩阵，I是单位矩阵。

得到最优控制增量后，取第一组最优控制增量Δu(k)，通过插值法即可得当前时刻的最优控制输入：

u(k)=u(k-1)+Δu(k)

(21)

当求得的当前时刻的控制输入u(k)作用到控制系统中去，再进行下一步的优化求解，如此循环执行下去即完成了预测控制的滚动修正问题。将每一步所求得的最优输入量值作用到系统中，得到当前时刻的实际系统输出，循环递推即可完成对整个控制系统的预测控制。

3 实验验证及应用研究

为了验证提出的基于ELM-ARX组合模型预测控制算法的性能，从数据仿真验证实验和水箱实际控制实验应用两个方面进行验证。数据仿真验证实验方面主要是针对两输入两输出模型数据，进行Matlab软件仿真控制验证实验，验证提出的基于ELM-ARX组合模型预测控制算法的有效性；水箱实际控制实验应用方面，本文基于Visual Studio编程软件开发了基于ELM-ARX组合模型预测控制算法的控制软件系统，并将其应用于双容水箱过程控制系统上，完成预测控制算法测试实验应用研究，测试算法对工业过程进行控制的可行性。

3.1 仿真验证实验

为了验证提出的ELM-ARX组合模型预测控制算法的性能，选取BP-ARX组合模型[10]作为对比。针对如式(22)两输入两输出模型非线性系统[19]进行数据模型辨识与Matlab仿真控制实验。

(22)

建立上述两入两出系统的ELM-ARX模型与BP-ARX模型，分别采用两个模型进行预测控制仿真实验，进行400步预测控制，ELM-ARX组合模型预测控制算法与BP-ARX组合模型预测控制算法对比控制效果如图3到图6所示。

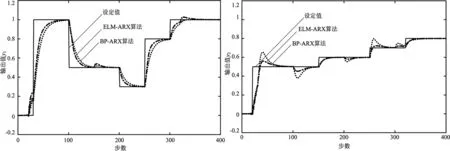
(a)被控变量输出值y1 (b)被控变量输出值y2

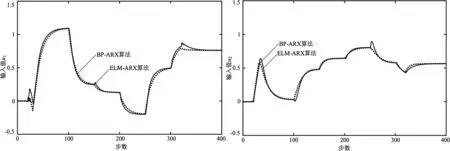
(c)操作变量输出值u1 (d)操作变量输出值u2

由图3数据仿真实验控制效果可知，采用本文提出的ELM-ARX模型与BP-ARX模型均可以使被控变量y1、y2较为平稳控制在设定值附近，但是基于本为提出的ELM-ARX模型进行的预测控制，非线性系统y1、y2超调量较小，表明本文提出的基于ELM-ARX组合模型预测控制算法的控制精度较高，可以获得更优的控制效果。

在第100步数时，图3(a)中被控变量y1设定值由1.0调整为0.5，图3(b)中被控变量实际值y2有一定波动，通过操作变量输入值和的调整，使得被控变量y1、y2快速稳定在设定值附件，并且基于ELM-ARX模型相比较BP-ARX模型使得被控变量实际值y2波动较小，体现出本文提出的基于ELM-ARX组合模型预测控制算法具有较强的干扰能力。

另外，在仿真控制程序运算时间方面，ELM-ARX模型运行时间为16.2541s，BP-ARX模型运行时间为65.5285s。可知，采用ELM-ARX模型的预测控制程序运算时间大大缩短，表明基于ELM-ARX的组合模型占用计算机资源小，这对于控制程序的长期在线运行是非常有利的。

3.2 水箱平台应用实验

为了进一步测试提出的基于ELM-ARX组合模型预测控制算法对工业过程进行控制的可行性，基于本文提出的理论算法，研发了模型辨识及预测控制软件系统。该软件系统与双容水箱控制平台通过OPC通信协议进行数据传输，可以完成对水箱平台数据的读取、存储、模型辨识以及控制变量操作值写入。

在水箱系统平台实验中，为了验证本文提出的基于ELM-ARX组合模型预测控制算法多入多出控制系统的可行性，选取上水箱和下水箱电动调节阀阀门开度作为操作变量，上水箱和下水箱液位高度作为被控变量，上水箱和下水箱连接处的进水阀门开度作为干扰变量。同时，由于水箱控制平台上水箱和下水箱通过连接处的阀门进行连接，此处阀门开度的大小对上水箱液位和下水箱液位均有影响，因此，连接处的阀门开度也是水箱控制平台实验两入两出模型的耦合变量。

基于水箱平台上水箱和下水箱电动调节阀不同的阀门开度阶跃响应，采集上水箱和下水箱液位高度多组数据。采用ELM-ARX组合模型辨识软件系统辨识水箱平台两入两出组合模型。将建立好的水箱控制两入两出平台组合模型参数载入预测控制软件中，设定预测控制软件系统相关参数，将水箱控制平台中被控变量水箱液位当前值和设定值通过OPC数据通信模块传入预测控制软件系统中，经过预测控制软件系统进行计算处理，给出当前操作变量水箱电动调节阀阀门开度的调整量，再通过OPC数据通信模块将电动调节阀阀门开度的调整量写入水箱控制平台，之后循环将水箱液位当前值传入预测控制软件系统中，直到水箱液位当前值趋近水箱液位设定值附近，即可完成水箱控制平台预测控制应用实验。水箱平台应用实验控制效果如图4所示。

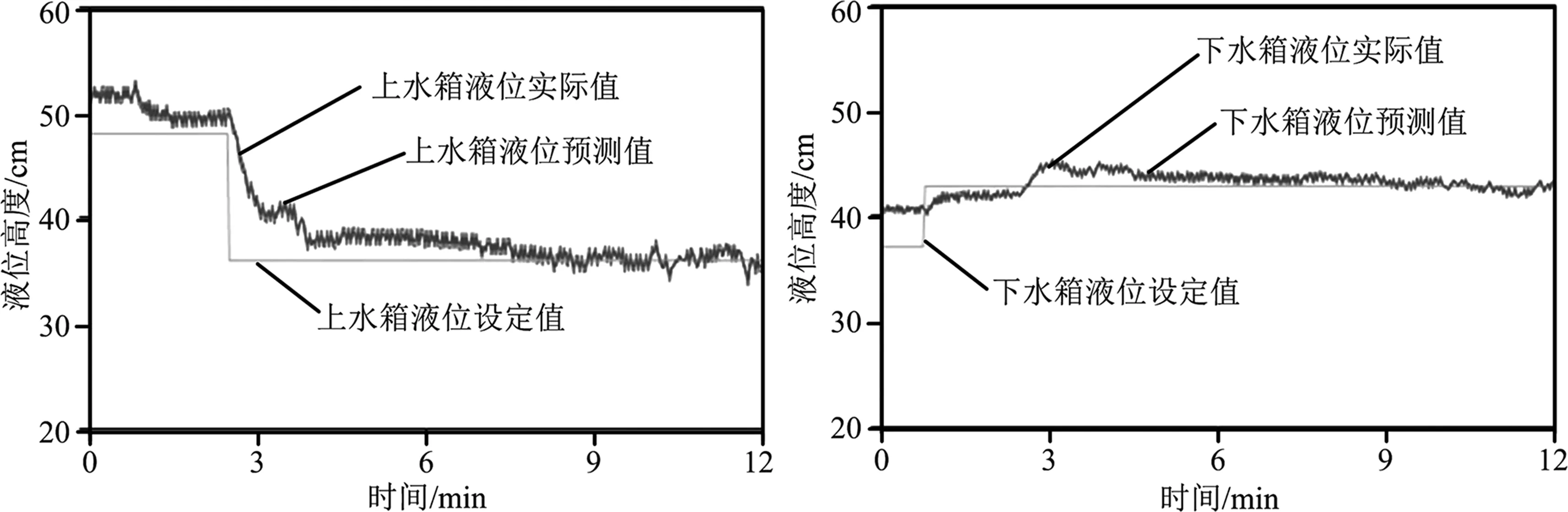
(a)上水箱被控变量液位高度 (b)下水箱被控变量液位高度

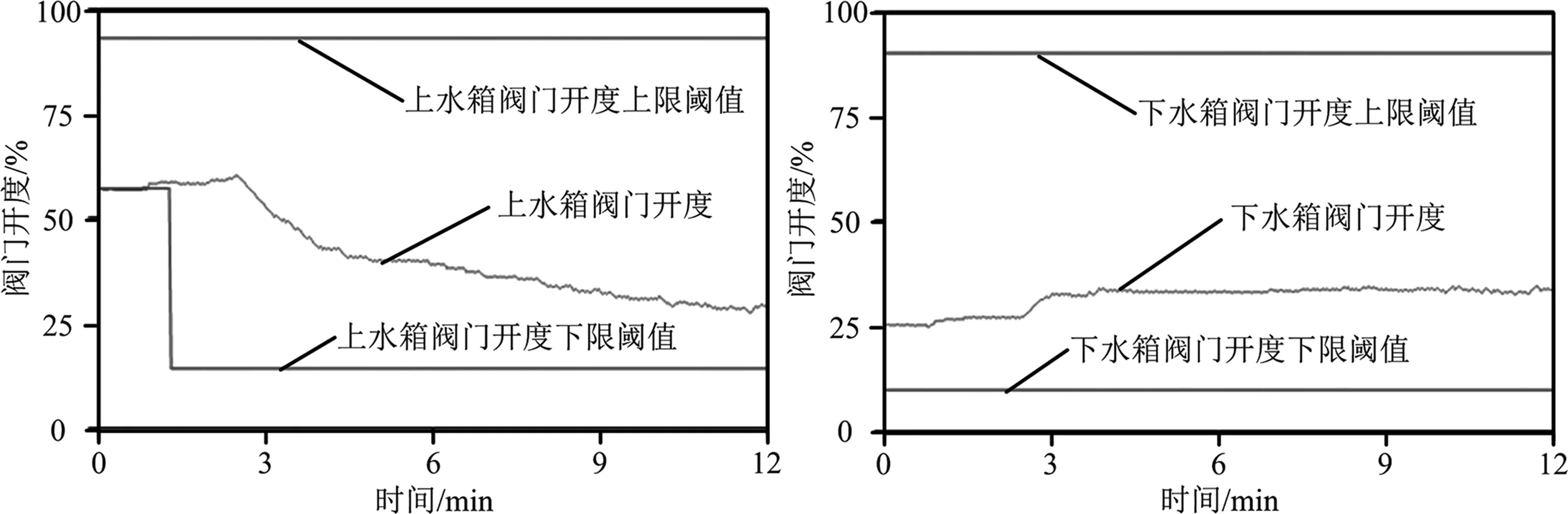
(c)上水箱操作变量阀门开度 (d)下水箱操作变量阀门开度

由图4水箱平台控制效果总体可知，基于ELM-ARX组合模型预测控制算法预测出的上下液位高度预测值与实际值偏差不大，当上下水箱液位高度在达到设定值之前，通过上下水箱阀门开度的预测调节，上下水箱液位高度稳定在设定值附近，达到预期控制预期效果。

在第1分钟左右，图4(b)中水箱平台控制效果下水箱液位设定值由37cm提高为43cm，图4(d)中下水箱阀门开度设定值小幅度提高。另外，由于有上下水箱连接处阀门开度耦合变量的存在，上水箱中的水通过连接处阀门流到下水箱中，使得上水箱液位高度实际值下降，通过预测控制软件系统算法计算，小幅度提高图4(c)中上水箱阀门开度。通过上述调整，使得上下水箱液位实际值均稳步贴近于液位高度设定值，未出现过大的超调。

第2.5分钟左右，图4(a)中上水箱液位高度设定值由48cm设定为36cm时，为了进一步验证本文提出基于ELM-ARX组合模型预测控制算法的多变量耦合控制的先进性，本水箱平台应用实验分别增大上下水箱连接处耦合阀门开度以及下水箱出水阀门开度，使得第2.5分钟左右图4(b)中下水箱液位高度实际值变大。为了稳定上下水箱液位高度，图4(c)中上水箱阀门开度大幅度降低，图4(d)中下水箱阀门开度小幅度提高。经计算，上下水箱液位高度最大超调量基本上均在9%左右浮动，甚至更小，控制效果明显。这充分体现出ELM-ARX组合模型进行过程控制的先进性和稳定性。

综上所述，基于ELM-ARX组合模型预测控制算法，将设计的预测控制软件系统应用于水箱控制平台，可稳定控制水箱液位，验证了本文提出的算法应用于工业过程控制的可行性。

结语

本文通过调节增益的方法实现了稳态模型和动态模型的有机结合，构建了控制系统的ELM-ARX组合模型；推导了预测步数内控制系统的被控变量预测输出值，提出了基于ELM-ARX组合模型的预测控制算法。Matlab数据仿真实验结果表明，采用ELM-ARX组合模型可以建立多入多出非线性系统控制模型，并取得较优的预测控制效果；基于本文提出的算法，研发了基于ELM-ARX组合模型的预测控制软件系统，进行了双容水箱平台应用实验，应用实验结果表明，设计的预测控制软件系统实现了双容水箱的精准控制以及多变量耦合控制，表明本文提出的基于ELM-ARX组合模型的预测控制算法具有较强的稳定性。提出的ELM-ARX组合模型预测控制算法以及研发的预测控制软件系统，不仅奠定了预测控制算法理论基础，也对实现工业流程精细化控制具有重要的实际意义和应用价值。