非接触式眼压计压平角膜过程的数值模型研究

林正皓, 王 灿, 张忠立, 秦亭亭, 刘贝贝, 冯齐斌, 洪 扁

(上海市计量测试技术研究院, 上海市在线检测与控制技术重点实验室, 上海 201203)

1 引 言

非接触式眼压计(non-contact tonometer, NCT)是一种通过射出可控空气脉冲压平患者眼角膜中央特定面积,再由内部计算机进行数据处理得到患者眼压的仪器[1]。相较传统接触式眼压计,NCT有着无需接触人眼、操作便利、测量时间短等优点,已在临床上逐步成为主要的眼压测量方式。为了判断NCT测量眼压时是否准确,对其工作情况及量值的溯源方法的研究极为必要。目前常用的溯源方法是通过制作标准模拟人眼,以内部增压或固定值眼压2种形式,复现一个标准的眼压值,再使用NCT去测量该标准模拟人眼,通过比较测量值和模拟人眼的标准值以实现溯源。针对模拟人眼复现的眼压值,文献[2]通过装置物理接触模拟人眼并压平,获得压平时的力值后与压平面积计算得到标准模拟人眼所复现的眼压值。这个方法可行的关键是需要控制压平模拟人眼面积与NCT空气脉冲的压平面积相同,以确保模拟人眼的变形量相同,即模拟人眼刚度的影响量一致。然而,对于NCT空气脉冲外部流场及压平角膜面积的研究仍为空缺。由于NCT空气脉冲的作用时间短(ms级),采用传统手段难以捕捉角膜被压平的瞬间及当时的压平面积,也无法对NCT的工作流场深入研究。随着计算机技术的高速发展,计算机仿真已经成为研究、设计、工程应用中不可或缺的重要手段[3～5]。通过双向流固耦合的数值仿真技术,能够实时分析呈现流体域和固体域紧密结合的复杂动态变化问题。

本文通过采用双向流固耦合的数值仿真技术,建立了NCT外部流场及角膜的三维瞬态数值仿真模型,研究NCT空气脉冲的流场特征及角膜在NCT作用下的动态变化过程。

2 理论及数值建模

2.1 NCT理论研究方法

NCT的空气脉冲符合流体力学中的射流理论[6],即高雷诺数流体自孔口、喷嘴等向外射入静止、同密度的流体中所形成的流动。通过将染色的水经过喷嘴射入静止水槽中(图1),可以看出射流自喷嘴进入外界静止流体后,随着射流行程的增加,射流边界越宽,流量越大,且存在一个外边界,在此边界之外的流体基本不受射流影响。

图1 染色水射流射入水槽中

对于射流的内部(图2),分为开始区域和基本区域2个部分,射流自喷嘴进入外界静止流体,首先是开始区域,区域内存在包含核心区的内边界,其内部射流速度基本与喷嘴处一致,速度衰减极小(图2喷嘴前三角区域);随后射流进入基本区域,此时射流轴心速度随距离衰减明显,断面速度分布逐渐扁平,各个射流断面的无量纲速度和无量纲距离具有相似性。根据NCT使用要求,测量时操作距离需保持在喷嘴前方11 mm处,通过圆截面喷嘴的湍流系数a=0.08及核心区域长度Sn计算公式可大致计算得被测角膜的位置处于射流的基本区域Sn。

图2 射流进入静止流体示意图

10.065 mm<11 mm

(1)

其中φ为喷嘴直径,mm。

在射流的基本区域内,每个行程固定的断面上,射流的速度分布仅仅为距中心线距离r的函数,从而可以推得其接触角膜后的压力作用范围也是一定的,进而可以研究角膜动态变化过程及压平时状态。

2.2 NCT的数值建模

对NCT空气脉冲的流场及其中的角膜建立数值仿真模型。模型如图3所示,由固体域(角膜与巩膜)和流体域(喷嘴内流体及外流场)2部分组合而成。

图3 非接触式眼压计数值仿真模型

2.2.1 固体域设定

固体域即角膜和巩膜部分。模型参数以人体统计数据的平均值为基准设定[7,9],角膜视为各向同性的弹性体,曲率半径R1=7.8 mm,密度ρ=1 000 kg/m3,弹性模量为0.86 MPa,泊松比为0.435[6],巩膜的曲率半径R2=11.5 mm,角膜和巩膜的厚度设定为0.5 mm。角膜的外表面为流固耦合计算的数据交换面,内表面施加了1个法向的压力边界条件以模拟人的眼压,压力大小取10、20、30、40、50 mmHg(目前眼科光学及仪器示值中仍在使用mmHg，1 mmHg=133.322 Pa,暂沿袭)，均匀覆盖NCT的量程。。网格总单元数47 215,节点数72 213,如图4所示。

图4 固体域模型及其网格

2.2.2 流体域设定

流体域包括喷嘴内一段流体及包裹固体域的外流场。NCT空气脉冲的最大雷诺数约为Re=2.56×104,流动视为不可压,计算采用SSTk-ω两方程模型,介质为空气,其密度ρ=1.225 kg/m3,动力粘度μ=1.789 4×10-5Pa·s。流场模型如图5所示,左侧小圆柱为非接触式眼压计喷嘴内的一段流体,直径为2.4 mm,喷嘴出口至角膜中心的距离为11 mm。空气脉冲自流场最左侧进入,经过喷嘴喷出进入外流场,最终到达角膜(固体域)。空气脉冲的速度曲线来源于型号为CoVis-ST的NCT实验数据[10],如图6所示。网格总单元数570 309,节点数103 862。

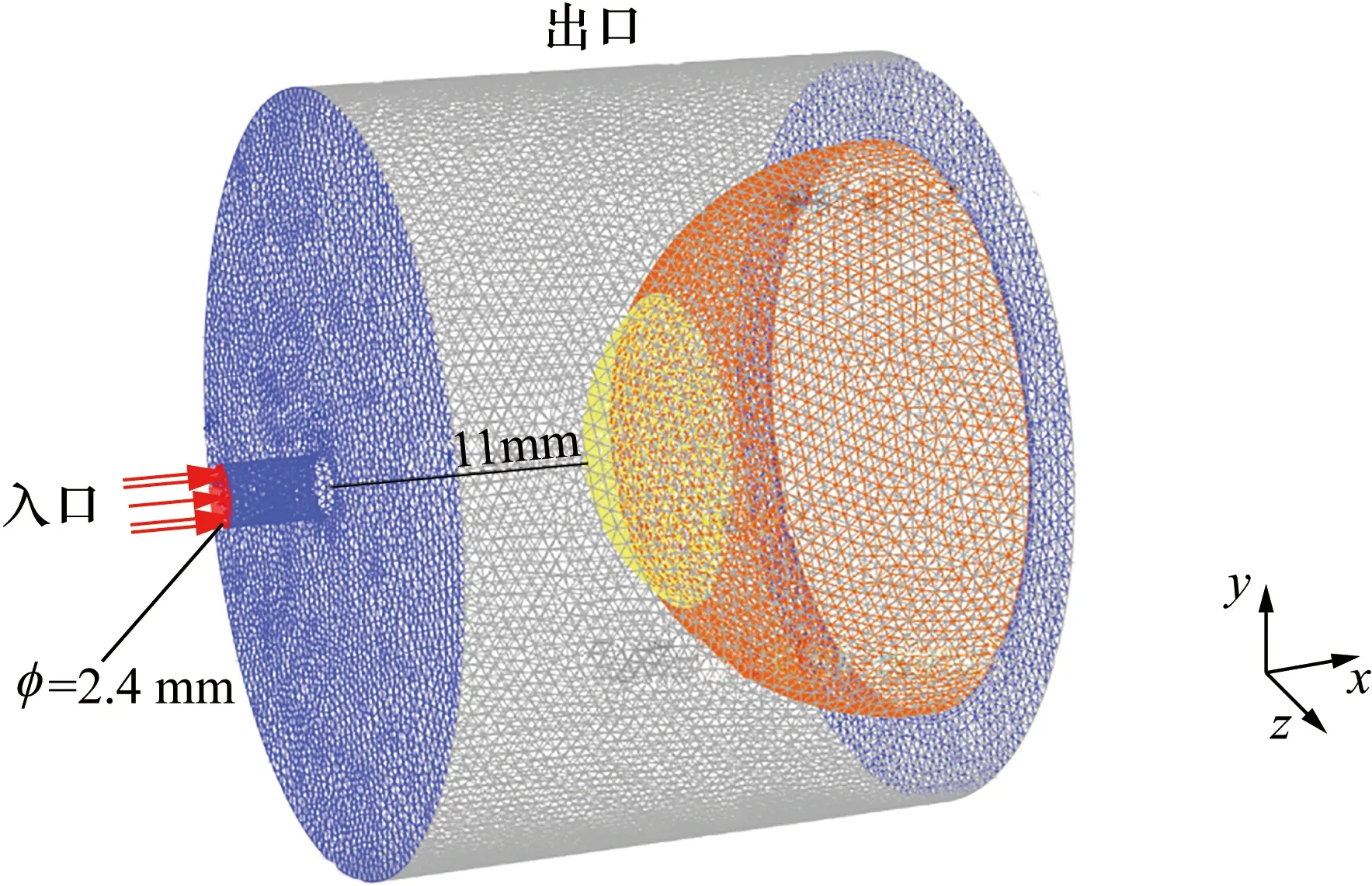
图5 流体域模型、网格、边界条件及关键参数的定义

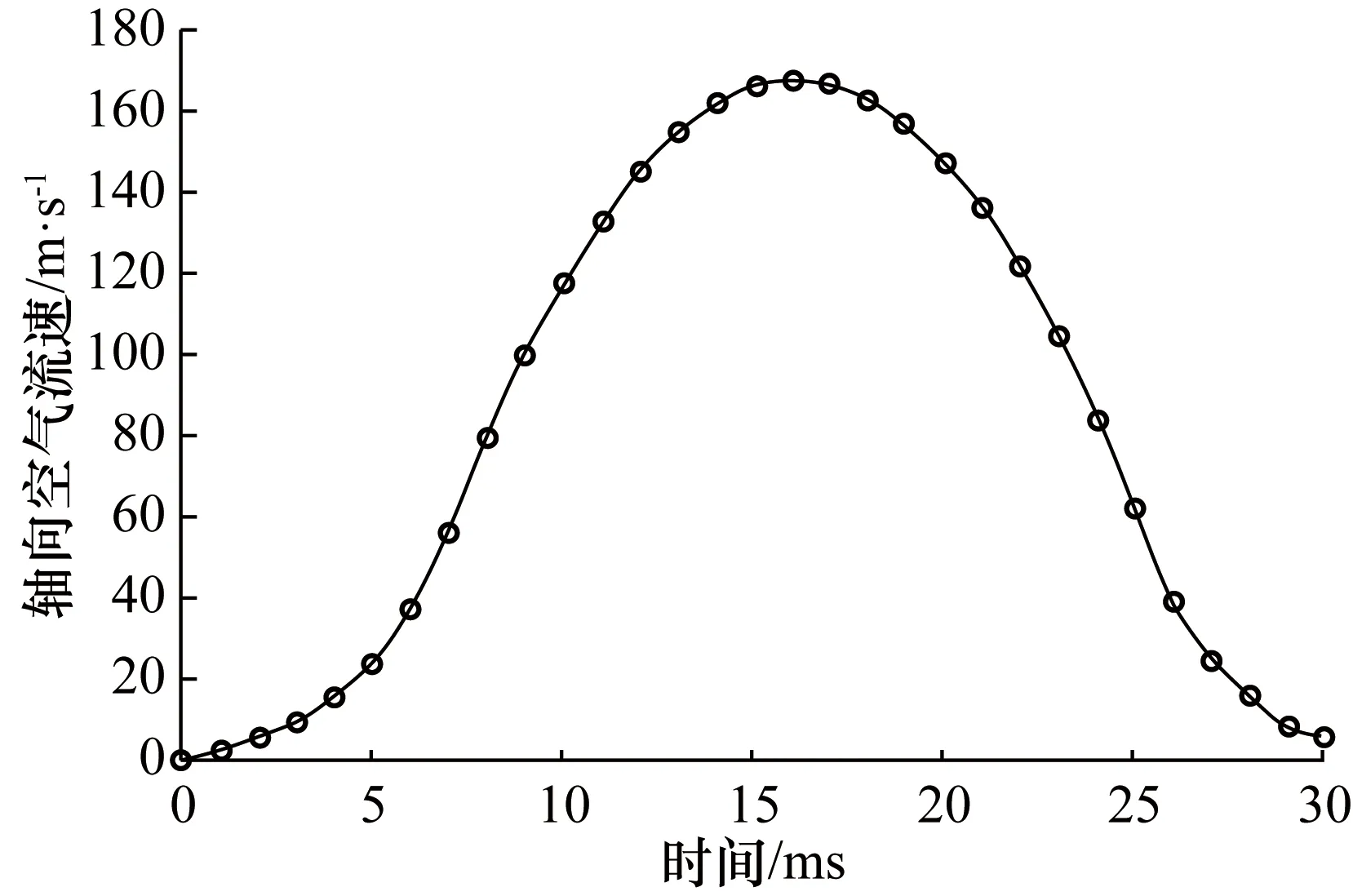
图6 非接触式眼压计喷嘴气流速度随时间变化曲线

2.2.3 耦合计算设定

流固耦合问题的求解方式主要有两类：分离求解和直接求解[11,13],本文通过数据交换模块联合固体、流体2个求解器分离求解。流体求解器负责流场压力、速度、温度等物理量的计算;固体求解器负责位移、应力、应变等物理量的计算;数据交换模块则负责以异步传递的形式更新固体、流体2个求解器中的共同变量,流体求解器计算解出力值,将其作为载荷传递给固体求解器;固体求解器计算解出位移值,再将其作为载荷传递给流体求解器,以达到双向流固耦合求解。外流场与固体域的接合面为流固耦合计算的数据交换面,同时设定了动网格[14],使流体域数据交换面在固体域计算过程中变形时,仍然能够时时“粘附”在固体域上,以保证流固耦合计算顺利进行。时间步长由数据交换模块统一控制,设定为0.05 ms,计算停止时间为16 ms。

图7 双向耦合计算设定框图

3 结果及分析

3.1 流场分析

根据气体射流理论,在整个射流范围内,任意一点A的压强等于周围静止流体的压强,则沿轴向任意断面间的动量守恒,即：

(2)

式中：ρ为流体密度;r0为喷嘴半径;v0为喷嘴处流速;r为距离中心轴的距离;v为r处的速度;R为当前截面的半径。因此可以由上式及无量纲速度、距离的相似性计算得到基本区域内射流轴心速度vm的理论值：

(3)

式中：x为点A距喷嘴的距离;a为湍流系数。取眼压为10 mmHg时的流固耦合计算结果。

16 ms时的射流轴心速度理论值和仿真值见图8所示。从图8中可以看出仿真结果很好体现出了在核心区内射流的轴心速度基本没有衰减的特性;从核心区过渡到基本区域时,仿真计算结果中曲线的变化趋势也与理论计算的较为相符,但随后仿真计算的速度曲线迅速衰减至0,这是由于流场中存在角膜这一障碍物导致的。

图8 数值仿真与理论计算的轴心速度比较

图9给出了不同时间下的射流轴心压力、速度曲线,从轴心速度曲线中可以看出,不同时间下射流都存在核心区,且核心区内流体速度基本没有衰减,到达基本区域后,流体遇角膜而速度急剧衰减至0,与理论一致。不同的是,射流初始核心区域较理论值小,但随着时间的推移,轴心速度曲线终点不断向右推移,射流的核心区域不断增加,这是由于在角膜变形较小甚至没有变形时,角膜前端中心位置位于射流的理论核心区附近,致使射流遭遇障碍物速度迅速衰减至0,核心区长度受此影响变小;而在16 ms时,眼压为10 mmHg的角膜受压变形严重,给予射流充分发展的空间,此时的核心区长度与理论相符。轴心压力曲线图与速度图类似,射流核心区内压力分布都为0,与理论一致;到达基本区域后,压力迅速升高,是因为射流遇角膜后速度滞止为0,使压力升高。同样,由于角膜变形逐渐加剧,压力曲线的终点随时间向右推移。

图9 不同时间的轴心速度、压力曲线比较

由于喷嘴发出的空气脉冲速度随时间而变大,因此图9中压力、速度曲线随时间推移而增高,速度图中各个曲线起点的轴心速度即为对应时间喷嘴激发的空气脉冲速度。图10为T=9.35 ms时流场中的压力、速度分布云图,可以直观地体现到图9的曲线变化趋势。

图10 流场压力、速度云图 (T=9.35 ms)

图11为眼压10 mmHg,不同时间的流场速度灰度云图,可以清晰看出射流在不同时间下的内外边界。射流的外边界基本不随着时间变化,角度约为8.4°;内部边界角度在9.35 ms时约为4.9°,由于16 ms时角膜形变严重,核心区长度增加,内边界角度收窄,约为4.6°。

图11 不同时间的射流区域比较

3.2 角膜的动态变化过程

通过流固耦合的仿真计算完整获得了不同眼压下,0～16 ms时间段内角膜受NCT空气脉冲影响的动态变化过程,以眼压为10 mmHg的情况为例(图12),可以观察到空气脉冲自喷嘴发出击中角膜,并于T=9.35 ms时吹平角膜,之后由于空气脉冲继续变强,角膜逐渐受压内凹这一完整的变化过程。

图12 角膜受空气脉冲影响的动态变化

图13为角膜在不同时间下的变形及表面压力分布曲线,变形曲线图纵轴的变形量指角膜上的点x轴坐标的负值,变形量为正,角膜外凸,变形量为负,角膜内凹。首先观察考虑16 ms以外的结果,可以看到角膜的中心区域变形最大,其变形量随时间的推移而增加,在距离角膜中心约2 mm以外的部分基本不受空气脉冲的影响而变形。从角膜表面压力分布图中同样可以看到,距离中心越近,角膜受到的压力越大,随着距离的增加,压力迅速衰减,在距离角膜中心约2 mm处压力衰减至0,并开始产生一小段负压区域。随时间推移,压力曲线中心峰值不断增加,但压力在中心区域内的衰减速度也相应增加,皆在距离角膜中心约2 mm处压力衰减至0,随后产生负压区域。而对于16 ms的结果,由于角膜内凹变形量过大,带动边缘部分变形,使变形范围有所扩大,同样压力曲线的峰范围也相应扩大,零压负压区域向外移动,整体趋势仍然与其余结果一致。

图13 不同时间下的角膜变形及表面压力分布

3.3 不同眼压下的结果比较

为比较选择的5个眼压点的角膜压平时的状态,将0～16 ms时间段内,角膜中心区域即将开始产生凹陷,且凹陷随后将不再恢复原位的最终时刻作为角膜的压平时间进行分析,各个眼压点的压平时间见表1所示。由表1可以看到随着眼压的增大,空气脉冲压平角膜所需要的时间越长,这与眼压计喷嘴出口空气脉冲速度随时间增大的特性相符。

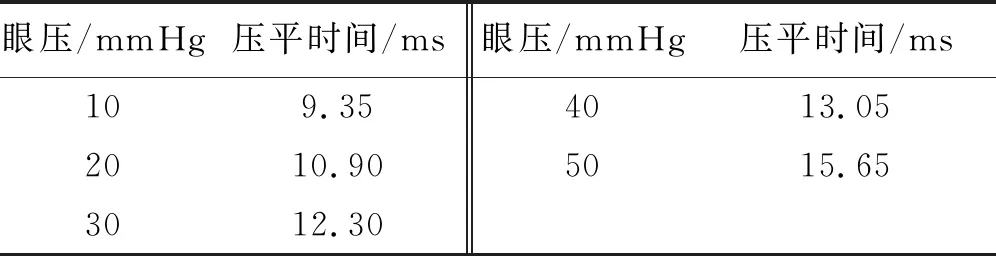
表1 不同眼压下的角膜压平时间

图14与图15分别为不同眼压的角膜初始状态曲线与压平状态曲线。由于此次角膜设定为线弹性模型,角膜初始状态会受到眼压的影响,图14中50 mmHg的初始状态曲线相比其他几个小眼压点有较明显的凸出。因此,图15中50 mmHg角膜压平时的轴向位移与其余曲线相比值更小,是因为其在初始状态下比其余眼压的角膜更为凸出。从图15中还可以看出,角膜的压平直径在不同眼压点下变化不大,在所选的5个眼压点下角膜压平直径基本处于3.2～3.6 mm的区间内,与美国青光眼研究基金会(GRF)的NCT压平直径[15]一致。

图14 不同眼压的角膜初始状态的比较

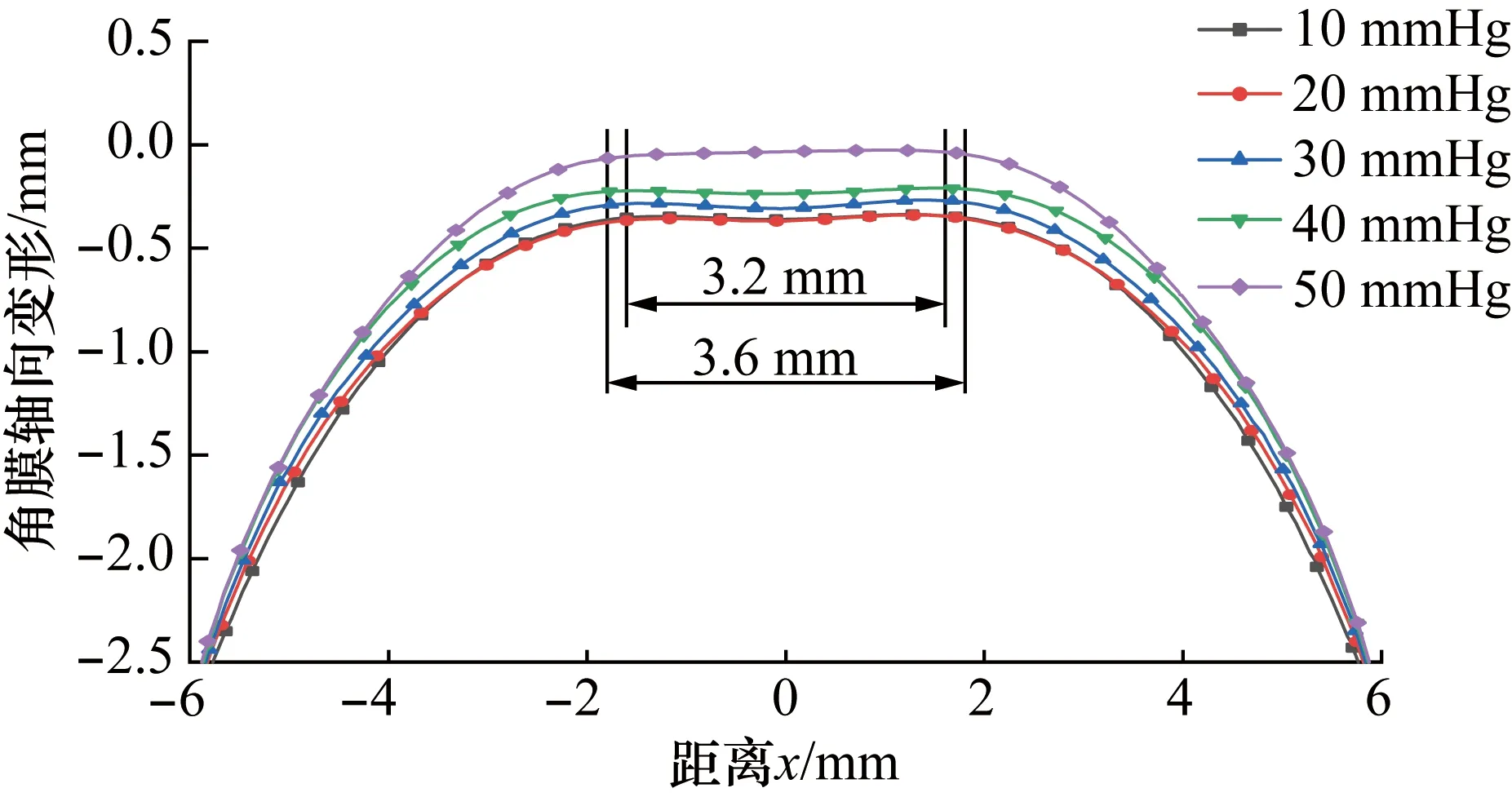
图15 不同眼压的角膜压平状态的比较

为了验证NCT外部流场及角膜的三维瞬态数值仿真模型，上海市计量测试技术研究院研制了一套模拟人眼角膜及配套装置,并将其经过特制的3.6 mm直径的圆形压平头压平溯源,且将溯源后的装置在各医疗机构中实地测试,获得了与临床结果相符的结论[2]。具体溯源过程采用了转矩平衡的方法,通过研制的L型平衡支架，将压平头压平模拟眼时的压力传递至支架另一端的高精度电子天平上,实时、稳定地获得不同眼压状态模拟眼与外部压平压力的对应关系。

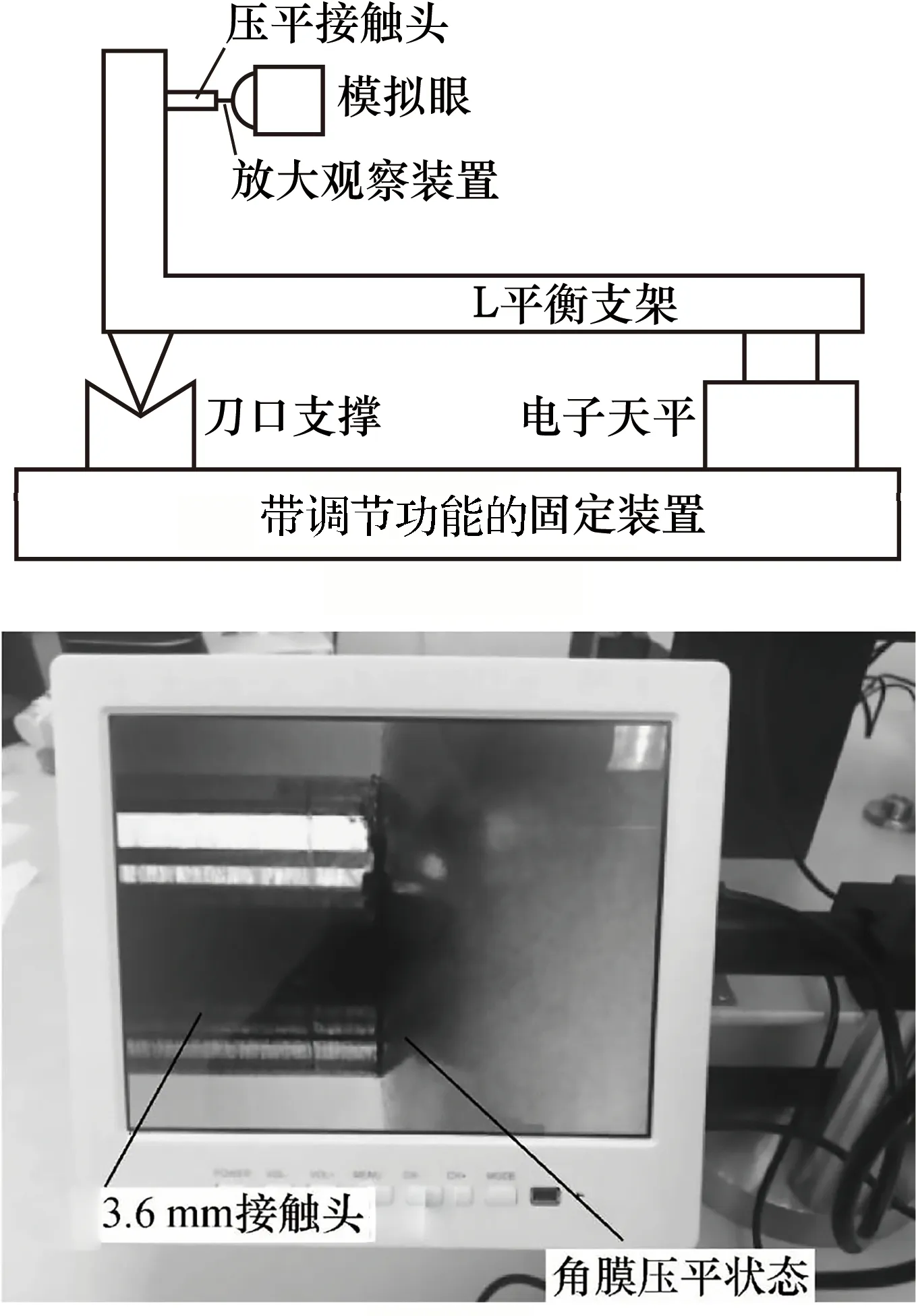
图16 溯源实验装置[2]

为进一步验证溯源时压平直径对测量眼压的影响,采用2个不同直径的压平头,以相同方法对装置进行溯源。压平头直径为3.06 mm和3.2 mm, 3.06 mm压平头采用Goldmann眼压计的标注压平直径, 3.2 mm压平头采用仿真结果区间的最小值,以验证与直径为3.6 mm的压平头的结果差异。图17中从左至右依次为3.06、3.2、3.6 mm的压平头。

图17 压平头

图18为3个不同压平头溯源得到的测量眼压数据及变化曲线。由图18可以看出压平头直径的缩小对测量眼压有增大的作用,3.06 mm压平头溯源得到的测量眼压与3.6 mm的数据相比,其在每个测点上已超出约5.7～9.6 mmHg眼压值,同时其偏差随被测眼压的增大而增大,平均变化率达到31.4%;而3.2 mm压平头溯源得到的各个测点的数据与3.6 mm的数据相比较大,但仍然比较接近,其测量眼压在最初的测点上偏差最大,达到3 mmHg,随后其差值随被测眼压的增大逐渐减小,最终测点上偏差为1.2 mmHg,平均变化率11.8%。溯源用压平头直径的减小总体上会使测量眼压增大,然而当直径从3.6 mm减小至3.2 mm时,测量眼压随被测眼压的增加会逐渐"收敛"到3.6 mm压平头的测量眼压上,而当直径进一步减小至3.06 mm时,测量眼压将不断增大,被测眼压越大,其误差越大。验证了溯源时控制压平头直径的重要性,当压平头直径在3.2～3.6 mm时,对测量眼压的影响较小,同时验证了仿真结果中的压平直径区间。

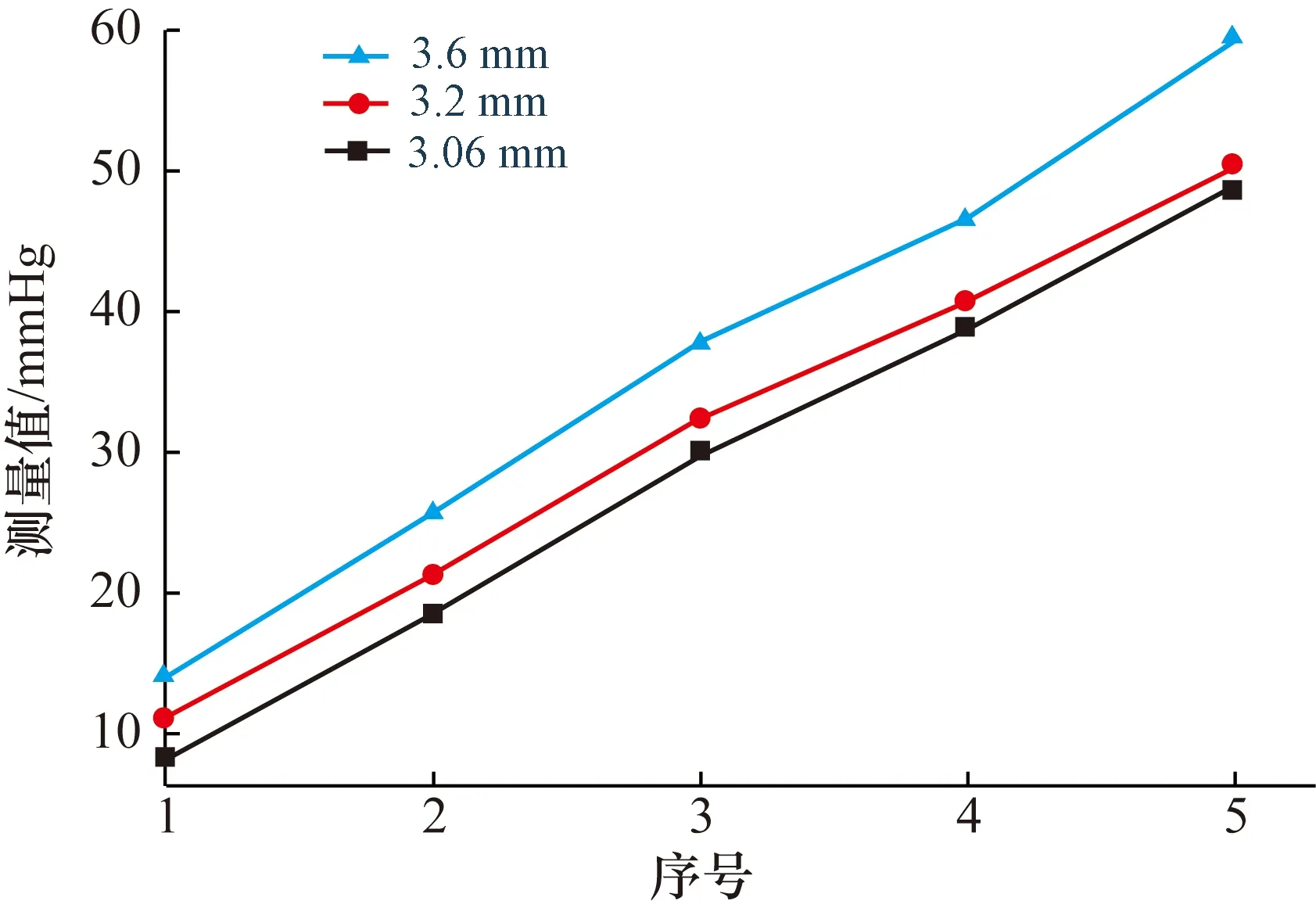
图18 不同压平头的眼压数据比较

4 结 论

1) 建立的数值模型能够有效研究NCT空气脉冲压平不同眼压的角膜的动态变形过程,角膜的压平时间随眼压的增加而增加,但不同眼压的角膜压平直径变化不大,角膜压平直径3.2～3.6 mm时,结果与GRF的相关文献中的数据一致,验证了模型的有效;

2) NCT的流场符合射流理论,存在核心区、内外边界等特征。外边界约8.4°,内边界由于角膜受压变形,其角度随时间变小;由于流场射流的特性,角膜表面的压力集中在中间区域,在距角膜中心2 mm处时,压力基本衰减至0,随后会产生一小段负压区域;

3) 根据数值模型的结果进行了相关的实验,当压平直径为3.2 mm时,测量眼压与压平直径为3.6 mm时差异不大,偏差随着被测眼压的增大而减小,平均变化率为11.8%;当压平直径为3.06 mm时,其测量眼压与压平直径为3.6 mm时有较大差异,同时其偏差随被测眼压增大而增大,平均变化率达到31.4%,侧面验证了上述角膜压平范围的合理性。