基于电磁热多场耦合的直埋电缆导体温度与载流量计算

王彦楠， 李 铮， 杨鹏飞， 刘 伟

(北京智芯微电子有限公司，北京 100089)

1 引 言

随着电力工业的发展，电网改造工程的实施，地下电缆系统已成为城市配电网的重要组成部分，对电缆温度场及载流量的准确计算对电缆系统安全经济运行有着重要的意义[1]，而电缆的敷设方式会对电缆导体温度和载流量产生较大的影响[2]。此外，相比有热回填敷设，土壤直接埋设时的电缆更不容易散热，电缆长期处在非正常的工作温度，会加速电缆绝缘老化，严重时甚至会引发火灾，对输电线路的安全稳定构成威胁，但如果选用导热系数较高的热回填，则会增加成本[3]。因此，正确计算电缆导体温度、载流量及确定合理的电缆敷设方式具有重要意义。

目前，地下电缆系统温度场和载流量的分析主要包括两种方法。一种是基于IEC 60287标准下的解析法[4～6]。文献[7～10]分别采用对比分析、梯形热网络模型、传热模型、场路结合等方法研究电缆温度场，并应用于土壤直埋和隧道等不同电缆敷设场景中;姜小兵[11]通过分析电缆结构和传热过程，建立电缆的集总参数热路模型，所提模型可准确计算电缆温升。基于IEC标准计算的这几种方法虽然得到的结果较为准确，但引入了大量的非线性方程，导致计算效率低，而且对分层方法和参数计算要求较高。第二种是数值分析法[12]，例如有限元法、有限差分法、边界元法等。李红雷等[13]采用有限元法建立电缆通道温度场仿真模型，计算了双回线工况和N-1工况下的温度场分布，并分析了周期性负荷对通道温度波动性的影响，得出恶劣环境下电缆导体温度和隧道空气温度均满足电缆安全运行的条件;为优化电缆的敷设方式，唐科等[14]基于传热学原理，利用有限元软件分别对地下直埋单芯电缆单根和三相敷设时的温度场进行了仿真，提出了利用单根电缆温度得到三相电缆温度的方法;张智辉等[15]结合有限元分析软件和MATLAB软件建立电缆群温度场仿真模型，以等负荷电缆群中最热电缆导体温度最低为依据，优化多回路电缆群的布局方式;李萌等[16]通过有限元分析法建立了电缆的多物理场耦合模型，分析了电缆沟内电缆不同敷设方式对电缆温度场及载流量的影响。相比解析法，数值分析方法具备应用广泛性强、模拟实际工况能力强、多物理场耦合分析等优点。

在上述研究工作的基础上，本文基于COMSOL Multiphysics®软件搭建了地下电缆系统电磁热耦合模型，重点分析了敷设深度、相间距离、热回填和相序对电缆导体温度和载流量的影响，提出了合理的电缆布局方案；在此基础上，利用多元线性回归模型，得到了不同影响因素的强弱程度，对电缆敷设工程具有一定的参考价值。

2 热路解析模型

基于IEC 60287标准建立的热路模型已经用于求电缆稳态额定载流量，电力电缆的热路模型如图1所示[17]。

图1 电力电缆温度场热路模型

电力电缆温度场热路模型中，Wc为电缆导体单位长度的损耗；Wd为导体绝缘单位长度的介质损耗；n为电缆的芯数；RT1为电缆绝缘层单位长度热阻；RT2为绕包层单位长度热阻；RT3为外护套单位长度热阻；RT4为电缆表面和周围煤质间单位长度热阻；λ1、λ2分别为电缆金属套及电缆铠装层损耗在电缆所有导体总损耗的占比。

根据热路模型，电力电缆载流量I可以由式(1)计算，式(1)的变形也可求得电缆导体温度。

(1)

式中：Rc为最高工作温度下导体单位长度交流电阻；Δθ为高于环境温度的导体温升。

交流电阻Rc可以由直流电阻、集肤效应因数及邻近效应因数表示：

Rc=Rdc(1+ys+yp)

(2)

式中Rdc为单位长度导体的直流电阻值，其可通过式(3)求得：

Rdc=Ro×[1+α20(T(x,y)-Tr)]

(3)

式中：Ro及α20是导体在20 ℃时的直流电阻和导体材料的温度系数；Tr为参考温度，取20 ℃；T(x，y)为导体的极限工作温度。

集肤效应和邻近效应因数ys和yp由以下关系确定[18]：

(4)

(5)

(6)

(7)

式中：f为电流频率；dc为导体直径；s为两个导体轴心之间的距离；ks、kp分别为集肤效应和邻近效应校正因子。

单位长度电缆绝缘层的介质损耗由式(8)计算：

(8)

式中：ω=2 πf；tanδ为工频下的绝缘损耗因数；Uo为电缆绝缘层承受的电压；Co为单位长度电缆的电容。

3 电磁热耦合模型

3.1 传热学理论

地下电缆系统的稳态温度场，属于二维稳态传热问题，热传递的微分方程为：

(9)

式中:t为电缆的温度；Qv为单位体积内电缆的生成热；λ为导热系数。当Qv=0时，表示为无热源区域。因有限元法不容易对开区域求解，将其转变为等价的闭区域再求解。从现阶段研究成果来看，一般认为电缆产热不影响电缆1.2 m外的土壤温度，因此设定距离电缆1.2 m及以外均视为深度土壤，深度土壤温度为26 ℃。

传热问题计算涉及的3类边界条件有[19]：

第一类边界条件：恒定边界温度

T|τ=Ts

(10)

式中：τ为积分路径；Ts为土壤的下边界属于恒定边界温度，深层土壤的温度为一恒定值。

第二类边界条件：边界法相热流密度

(11)

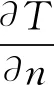
第三类边界条件：对流换热条件

(12)

式中:h为闭区域的上边界和周围空气的对流换热系数；To为闭区域上边界温度；Tw为空气温度。考虑到北京夏季环境温度38 ℃时，最影响电缆的安全运行，因此以环境温度38 ℃为例。

在式(9)～式(12)的理论基础下，通过有限元仿真可以得到其温度分布情况；同时设置电缆导体的最高工作温度为90 ℃，相对容差为0.1，通过有限元分析软件内的优化算法求得电缆载流量。

3.2 模型假设

在保证计算准确度的前提下，减少模型计算量，作如下简化：①电缆处于无限长空间，可在电缆敷设的任一处截取1个面，认为截取的面是绝热面；②电缆各层及材料属性为各向同性均匀介质；③土壤外表面的对流散热为自然对流散热。

3.3 计算实例

电缆直埋敷设方式的几何模型如图2所示，由于电缆的长度相对于其截面积可认为无限长，采用二维电缆截面模型即可反映电缆导体及其周围的温度分布。为保证电缆随敷设深度变化时距离截取土壤下边界始终大于等于1.2 m，选取土壤深度为 3 m；因电缆横向温度场为非主要研究对象，且不影响计算结果，为减少仿真运行时间，选取土壤宽度为2.4 m；热回填的面积为(0.492m+L)×0.984 m，L为两条电缆之间的间距，可以改变大小；电缆导体距离热回填的下边界和左右边界分别为0.146 m和0.246 m；H为电缆埋设的深度，同样可以改变大小。

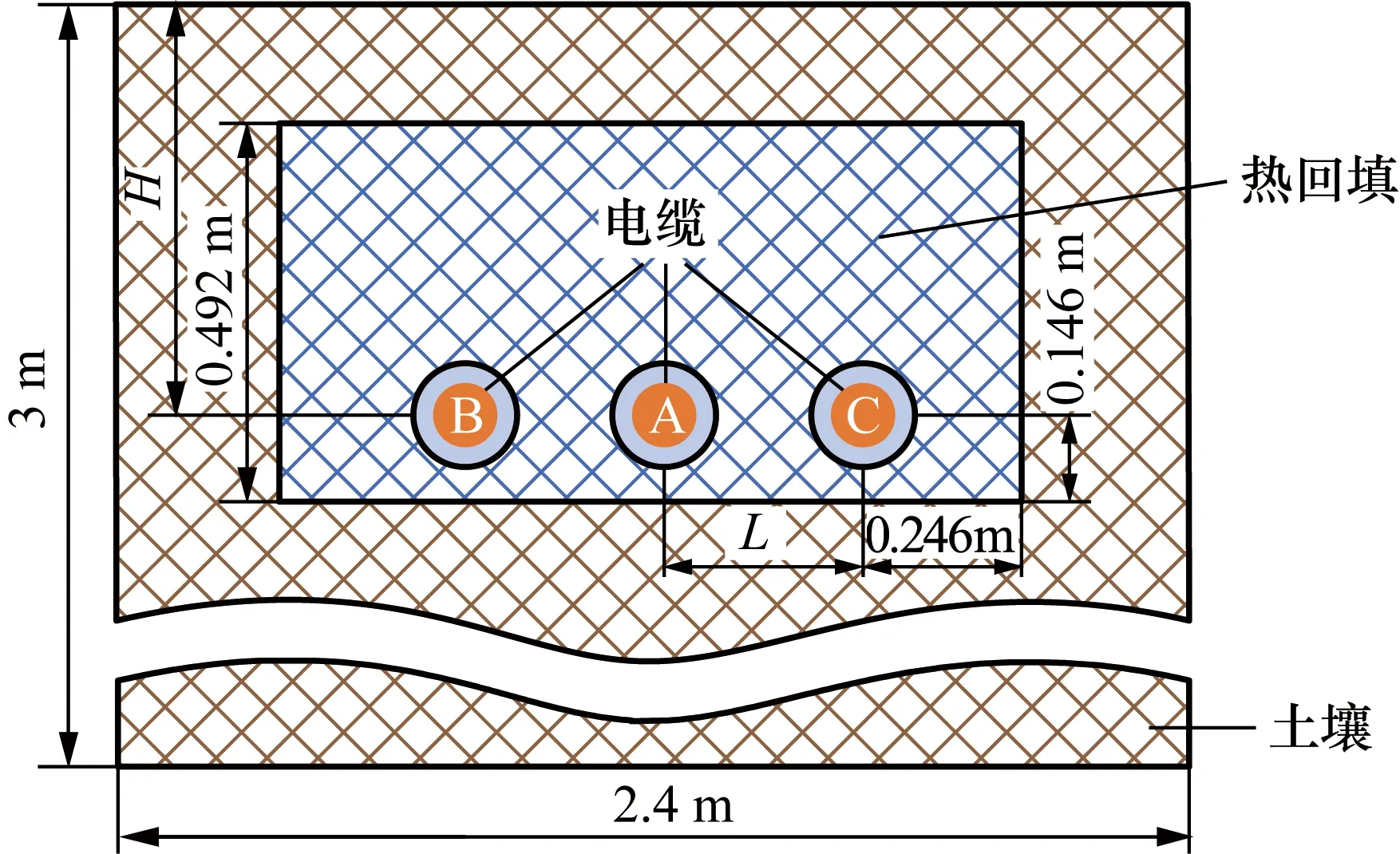
图2 直埋电缆几何示意图

敷设电缆型号为YJW 03 64/110 1×500[20]，其结构参数见表1。

表1 电缆结构及物理参数

设定A相电流相位为0，B相超前A相120°，A相超前C相120°，仿真模型关键参数见表2。

表2 仿真模型关键参数

4 模型验证

实际应用中最关注的是当电缆导体温度为90 ℃时的电缆最大载流量，因此为验证该电磁热耦合仿真模型的准确性，首先对单根电缆在土壤直埋、敷设深度不同时的电缆载流量进行求解。

电磁热耦合模型所计算出的载流量与IEC 60287标准下的热路解析模型计算结果的对比情况见表3。计算出同样敷设状态下的载流量，二者平均相差1.34%，满足工程实际的要求；如果忽略利用有限元法建模时，不可避免引起的误差，可近似认为两者相等。

表3 两种方法计算的载流量值对比

因此，通过对电缆敷设区域建立电磁热耦合计算模型，利用COMSOL进行电缆的温度场和载流量仿真计算是有效的，与理论计算结果基本拟合；而且与解析法相比，当仿真参数发生变化时，本模型可方便地通过修改相关参数得到与实际条件相对应的仿真结果，具有较强的实用性。

5 导体温度及载流量影响因素分析

5.1 敷设深度的影响

敷设深度决定了电缆距离地面的高度，直接影响电缆的散热。本节在前述构建的仿真模型的基础上，将电缆敷设深度作为单一变量，分析电缆回路各相导体温度和载流量的变化，计算结果如图3所示。

图3 敷设深度对电缆导体温度及载流量的影响

由图3可以看出，无论多大的敷设深度，A相电缆的温度始终高于其他两项电缆，是因为A相电缆处在3根电缆的中间位置，两边电缆的温度对中间电缆有热积累作用，而且由于临近效应，导致A相电缆损耗最大，产热量最大，因此A相电缆温度最高。

由3根电缆的导体温度曲线来看，敷设深度从0.8 m增大到1.25 m，电缆导体的温度均升高，表明敷设深度的增加不利于电缆导体散热。敷设深度由1.25 m增大到1.6 m，导体温度又呈现下降趋势，其原因是因为深层土壤温度值较低，对电缆的散热起到了一定的增益效果。

A相电缆在敷设深度为1.25 m时高达65.7 ℃，在敷设深度为0.8 m时为63.8 ℃，温差为1.9 ℃；A相电缆相对B相、C相电缆的最大最小温度差几乎相等。

从电缆载流量的角度来看，敷设深度的增加导致电缆载流量大幅度减小，折线的斜率逐渐减小，表明载流量的减小速度逐渐变慢。敷设深度从0.8 m增大到1.25 m，载流量减小了37 A，虽然随敷设深度的增加载流量略有回升，但与敷设深度为0.8 m时的载流量相比小了32 A。

因为电缆是长距离输电，挖掘较深沟道的人工成本较大，因此综合敷设深度对电缆导体温度和载流量的影响来看，选择电缆敷设深度时应宜浅不宜深。但根据地下电缆的敷设规范敷设深度要大于0.7 m，因此电缆的敷设深度选择0.7～0.8 m之间比较合适，且与常规敷设深度1.4 m相比，载流量上升了约4.8%。

5.2 相间距离的影响

电缆紧密排列或留有较小间隙排列时，单根电缆的温度场会影响其他电缆的散热，而且由于临近效应对电缆导体的交流电阻大小产生一定的影响，导致损耗不同，进而影响电缆导体及周围的温度场，因此合适的相间距离，一定程度上能减小导体的温度，增大电缆载流量。本文将电缆敷设相间距离作为单一变量，分析电缆回路各相导体温度和载流量的变化，计算结果如图4所示。

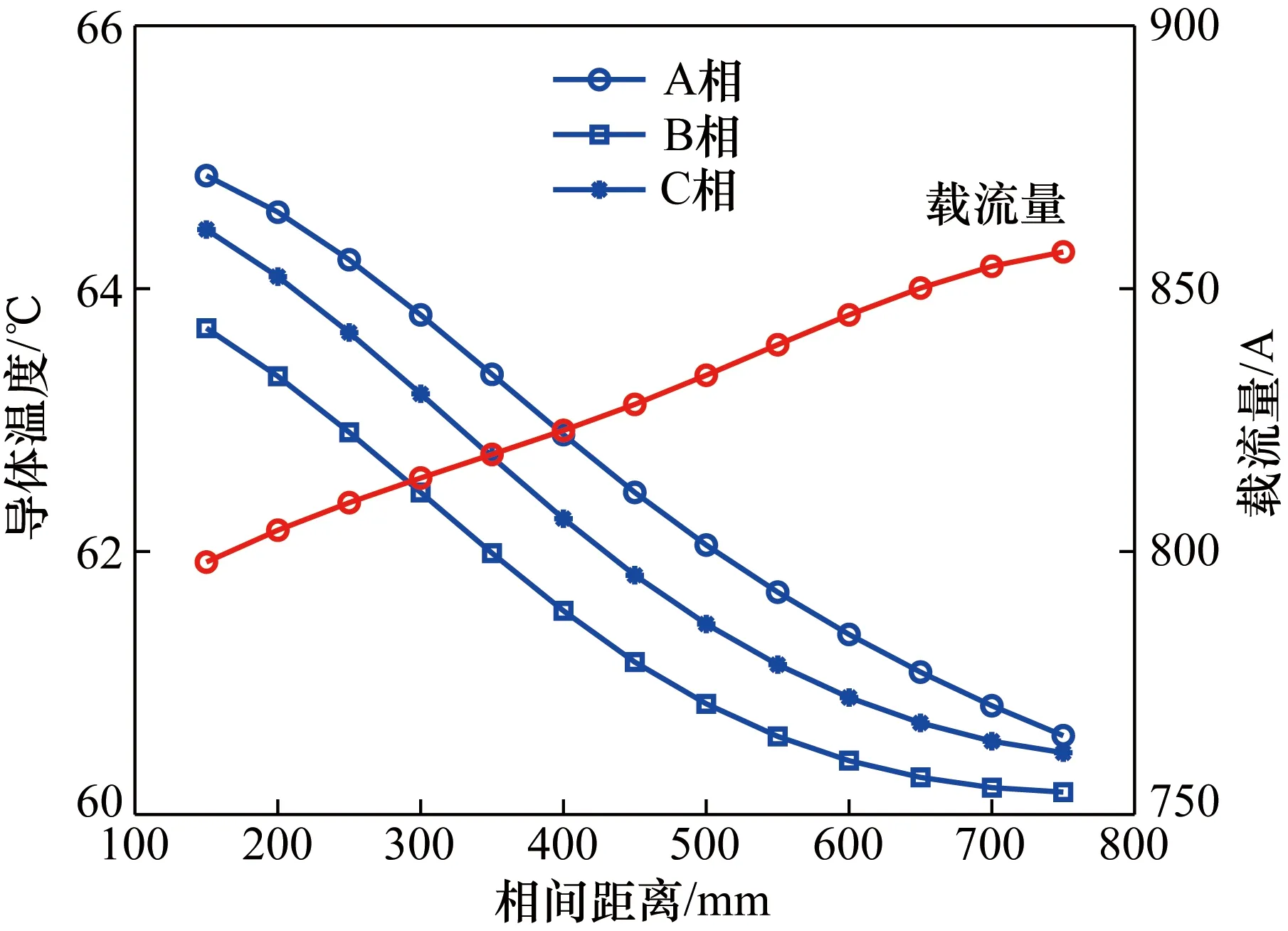
图4 相间距离对电缆导体温度及载流量的影响

分析图4可得，随相间距离的增加，3根电缆导体温度都减小，电缆载流量增大，表明相间距离的增大，有助于电缆的散热。

相间距离从150 mm增大到750 mm，A相电缆温度下降了约4.26 ℃，B相电缆温度下降了约3.53 ℃，C相电缆温度下降了约3.98 ℃，载流量上升了 59 A，表明相间距离对电缆导体温度及载流量还是有明显的影响。当相间距离大于750 mm时，3根电缆温度有趋于相等的趋势，因为3根电缆距离越大，临近效应越小，相互影响程度越低，因此3者之间温度差也越来越小。但实际工程应用中，考虑到工作难度，具体可以根据实际情况进行选择。

5.3 热回填的影响

地下电缆系统中，考虑电缆的散热情况，有时在回填土壤之前用比土壤导热系数较高的热回填首先埋设到电缆周围。本节将回填物导热系数作为单一变量，对比分析了纯土壤和不同导热系数热回填对导体温度、载流量的影响，见图5和图6所示。

图5 热回填导热系数对电缆导体温度的影响

图6 热回填导热系数对电缆载流量的影响

分析图6可得，使用导热系数为0.8 W/(m·K)的纯土壤时，电缆载流量为748 A，使用导热系数为1W/(m·K)的热回填时，电缆载流量为778 A，二者相差30 A，因此相比纯土壤，热回填对电缆散热有着更大的增益效果。

而且由图6可以看出，不同热回填对导体的散热效果有着显著的差异，但导热系数较高的热回填成本较高，因此有必要选择合适的热回填。

由图5和图6可以看出，热回填导热系数为 1 W/(m·K)时，A相导体温度为66.37 ℃，电缆载流量为778 A；热回填导热系数为2 W/(m·K)时，A相导体温度为62.52 ℃，下降了3.85 ℃，电缆载流量为827 A，上升了49 A；热回填导热系数为 3 W/(m·K)时，A相导体温度为61.11 ℃，电缆载流量为851 A，相比导热系数为2 W/(m·K)时，A相导体温度下降了1.41 ℃，电缆载流量增大了 24 A。热回填导热系数从1 W/(m·K)增大到2 W/(m·K)，B相、C相导体温度分别下降了 3.1 ℃、3.5 ℃；热回填导热系数从2 W/(m·K)增大到3 W/(m·K)时，B相、C相导体温度分别下降了1.1 ℃、1.2 ℃。

由此综合来看，热回填导热系数从1 W/(m·K)增大到2 W/(m·K)时，对电缆导体的降温程度和对载流量的增大程度，大于热回填导热系数从2 W/(m·K)增大到3 W/(m·K)，而且由图5和图6中曲线斜率也可以看出此趋势。

因此应选择导热系数约为2 W/(m·K)的热回填，既能保障其对电缆的散热效果，增大电缆载流量，也能节省一定的成本。

5.4 相序的影响

电缆的相序会影响子电缆护套的环流大小，改变电缆温度场分布，进而影响电缆载流量。针对本文的研究对象，电缆相序采用ABC排列或CBA排列，只是A相和C相调换了位置，从敷设场地的二维平面来看，对于电缆的温度场和电缆的载流量无影响，ACB排列和BCA排列、BAC排列和CAB排列同理，因此本文以相序为单一变量，研究3种相序排列方式对电缆温度场及载流量的影响，计算结果见表4。

分析表4可得，3种排列方式下，A相电缆导体最高温度发生在BAC排列方式，B相电缆导体最高温度发生在ABC排列方式，C相电缆导体最高温度发生在ACB排列方式，即无论电缆采用哪种相序排列方式，都是中间相电缆的导体温度最高。

此外，ABC排列方式下，除了B相导体温度最高，C相导体温度次之，A相最低；ACB排列方式下，除了C相导体温度最高，B相温度次之，A相最低；BAC排列方式下，除了A相导体温度最高，C相次之，B相温度最低。总之，除中间相温度最高外，滞后相电缆导体温度次之。

分析载流量的数据可得，无论哪种相序方式，对电缆载流量的影响不大。

5.5 影响因素的回归分析

多元线性回归是研究两种或两种以上变量间相互依赖的定量关系的一种统计分析方法[21,22]。由前述分析可以看出电缆载流量与敷设深度、相间距离、热回填导热系数有较强的线性关系，与相序无较大关系，因此本文通过多元线性回归，拟合出影响因素与载流量的关系方程，判断各影响因素对载流量的影响程度，同时分析出最优敷设方式，为直埋电缆敷设工程实践提供理论依据。

根据上述三个影响因素建立多元线性回归模型：

y=β0+β1x1+β2x2+β3x3

(13)

式中:自变量x1、x2、x3分别代表敷设深度、相间距离、热回填导热系数；因变量y代表载流量；β0为偏置项；β1、β2、β3分别为敷设深度、相间距离和热回填导热系数对载流量的影响权重。

基于python环境，通过广义的最小二乘法计算得回归模型：

y=767.771 578 8-0.051 048 591x1+

0.113 133 521 1x2+31.970 507 74x3

(14)

回归模型的好坏由模型评价参数来说明，R、MAE、RMSE、RRSE和ARE分别代表的是相关系数、平均绝对误差、标准误差、根相对误差和相对误差绝对值，模型评价参数见表5。

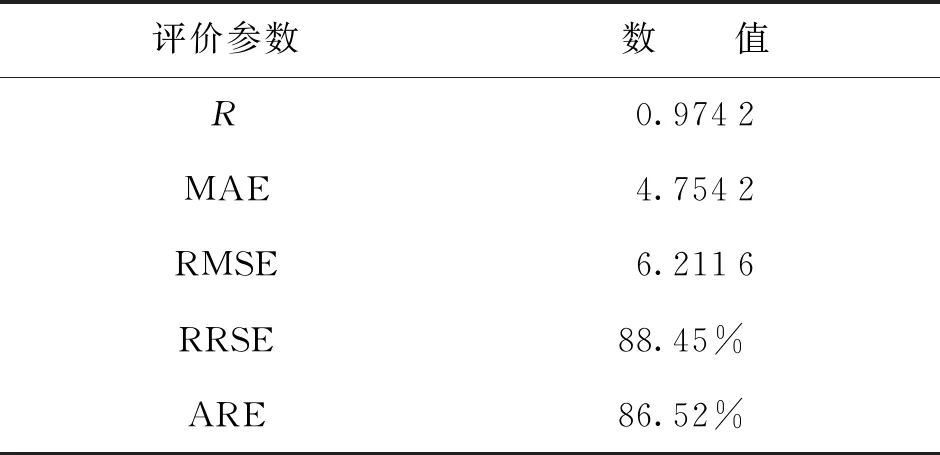
表5 模型评价参数

由此可见本模型具有较高准确度。针对回归模型与回归模型指标可知：热回填导热系数对电缆载流量的影响最为显著，相间距离次之，敷设深度最小。结合4.4节可知，以载流量最大为目的，最优的敷设方式为敷设深度为800 mm，相间距离为 750 mm，热回填导热系数为1.5 W/(m·K)，相序为BCA。

6 结 论

本文介绍了电缆温度场和载流量的计算方法，利用IEC标准下的热路解析模型验证了搭建的电磁热耦合模型的准确性；此外，应用该耦合模型分析了敷设深度、相间距离、热回填和相序与电缆导体温度及载流量的关系，得出如下结论：

(1) 电缆的敷设方式较大地影响着电缆导体温度及载流量，合理的布局方式和回填方案能够极大地帮助电缆散热，增加电缆的载流量；

(2) 敷设深度的增加使得热量不易扩散到空气中，导致电缆导体温度增加，电缆载流量减小，合适的敷设深度为0.7～0.8 m；相间距离的增大，减小了电缆间的相互影响程度，增大了电缆的散热，电缆导体温度减小，电缆载流量增大，因此工程敷设电缆时应适当地增大相间距离；热回填对电缆的散热效果远优于纯土壤，而且热回填导热系数越大，越有利于电缆的散热，提高电缆的载流量，但综合考虑热回填成本问题，确定了导热系数约为2 W/(m·K)的热回填性价比较高；无论电缆以哪种相序排列方式，都是中间相电缆温度最高，滞后相温度次之，超前相温度最低；

(3) 搭建多元线性回归模型，拟合出敷设深度、相间距离和热回填导热系数与电缆载流量的关系，分析结果为热回填导热系数对电缆载流量的影响最为显著，可为电缆敷设工程提供一定的参考。