长导轨直线度分段测量拼接方法研究

李 婷， 缪东晶， 李连福， 李建双， 钟 文，3

(1.湖南省计量检测研究院，湖南 长沙 410007； 2.中国计量科学研究院，北京 100029；3.中国计量大学，浙江 杭州 310018)

1 引 言

直线度是几何量测量领域中最基本的形位误差之一，长导轨的直线度是影响设备精度的最主要因素之一[1,2]，长导轨的直线度测量方法有很多种[3～7]，激光干涉仪由于测量精度高等优点在长导轨直线度测量中应用最为广泛。激光干涉仪测量直线度误差时，限于直线度测量组件分光镜的测量范围，一般直线度组件分为10 m短测量范围和30 m长测量范围2种规格，对于较长导轨的直线度进行分多段测量。激光干涉仪本身的数据漂移[8～10]导致单点重复性差，由于激光干涉仪摆放位置不同，导致获取的直线度曲线坐标系发生旋转偏斜等情况。

目前针对激光干涉仪分段测量长导轨直线度误差，通常采用的拼接方式为单点拼接方式和斜率一致平移拼接等方式[11]。事实上，在使用激光干涉仪测量直线度误差时，由于激光干涉仪受分辨率、折射率梯度的影响及直线度反射器的地形等[8～12]影响，在测量过程中不可避免发生数据漂动，单点测量重复性较差，用这些拼接方式可能带来较大拼接误差。减小直线度测量拼接误差的研究主要集中在如何提高局部测量精度、选取采样点等方面，如利用短平晶重构拼接[13]、应用大跨距和小步距法测量拼接[14]、选取采样点数与节距[15]、减少漂移[16]、较好利用直线斜率进行拼接[17]。贾立德等[18]使用短基准测量550 mm导轨直线度中应用坐标变换拼接方式测量较短导轨的直线度误差，研究了重叠测量区域二次采样点匹配误差对于测量误差的影响，但是坐标变换拼接方法对于需要改变激光干涉仪位置的长导轨和超长导轨是否适用，目前尚未见相关研究和验证报道。

本文针对中国计量科学研究院室内80 m长导轨(简称长导轨)，采用2台Agilent E1733A激光干涉仪同步进行直线度测量实验，一台干涉仪确定测量点位置，另一台测量该点直线度误差值，把直线度误差和位置视为该测量点坐标值，应用坐标变换原理进行拼接实验，来研究坐标变换拼接方法能否有效应用于长导轨的直线度拼接测量。

2 坐标变换拼接原理

激光干涉仪测量长度为L的导轨直线度时，受测量范围的限制，需要分为L1和L2两段进行测量(见图1)，2次直线度测量重叠部分为L12部分(其中L12>0，也称转换区间或测量重叠区域)，在2次测量中采用相同的测量节距，且在测量重叠区域L12内，L2测量点位置与L1测量点位置一致。

图1 分段进行直线度测量的示意图

对导轨在L1范围内进行的测量称为第1段直线度测量，每个测量点的直线度坐标为(X1i,Y1i,Z1i)其中X1i为第i个测量点的位置；Y1i为该点水平方向直线度；Z1i为该点垂直方向直线度。在L2范围内对导轨进行第2段直线度测量，测得第i点的直线度坐标为(X2i,Y2i,Z2i)。

激光干涉仪测量直线度的方式决定了在测量垂直方向直线度时Y=0；测量水平方向直线度时Z=0。第1段直线度垂直方向测量时坐标数据集也可写为(X1i,0,Z1i)。

在L12段，测量点坐标一致，其位置关系表示如下：

(1)

式中：X1m为第1段测量的第m个测量点位置；X2(1+n)为第2段测量的第1+n个测量点位置；X1(m+n)为第1段测量的第m+n个测量点位置。

坐标变换点>3时，可以通过公共坐标点数据计算出转换矩阵。假设测量重叠区域内测得的第1段直线度坐标矩阵为A，第2段的直线度坐标矩阵为B，通过2个坐标系下的转换坐标集A和B可计算出坐标旋转矩阵R和坐标旋转矩阵T：

A=RB+T

(2)

把第2段测量区域内L2范围内直线度测量坐标集(X2，Y2，Z2)转换至第1段直线度测量坐标系中，可用式(2)得到的R和T计算：

(3)

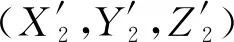
3 拼接区域选取实验及分析

使用激光干涉仪测量导轨直线度时，单点测量点的重复性较差，虽然匹配误差较小，但仍会影响坐标变换的精度。

转换区间公共点数越多拼接误差越小，但考虑工作量因素，实际测量中，重叠测量区域测量点数不可能无限增加，如何选取较小范围作为重叠测量区域来确保坐标变换拼接精度是坐标变换拼接方法的关键。

本文对长导轨的特性进行了分析研究，长导轨由1根5 m、20根4 m子导轨拼合组成，单根子导轨直线度<20 μm，相邻子导轨间由于存在一定夹角的安装误差。基于长导轨固有属性，将对单根子导轨上测得的直线度数据可能具有斜率一致的特性及相邻子导轨直线度拟合直线具有夹角固定的特性进行分析。

3.1 拟合子导轨特性分析

如图2所示，数据1和数据2均为激光干涉仪在0～20 m范围内测得直线度及各子导轨直线度的拟合直线曲线，对应单根子导轨位置的直线度测量数据拟合为直线，从图2中可看出：同一子导轨上在不同测量实验中，测得的直线度数据拟合直线具有较为一致的斜率值;2根子导轨之间具有固定夹角。表1和表2中给出了部分子导轨拟合直线的斜率和夹角值。实验结果与实际导轨物理特性相吻合。

图2 激光干涉仪在0～20 m范围内测得直线度及轨直线度的拟合直线

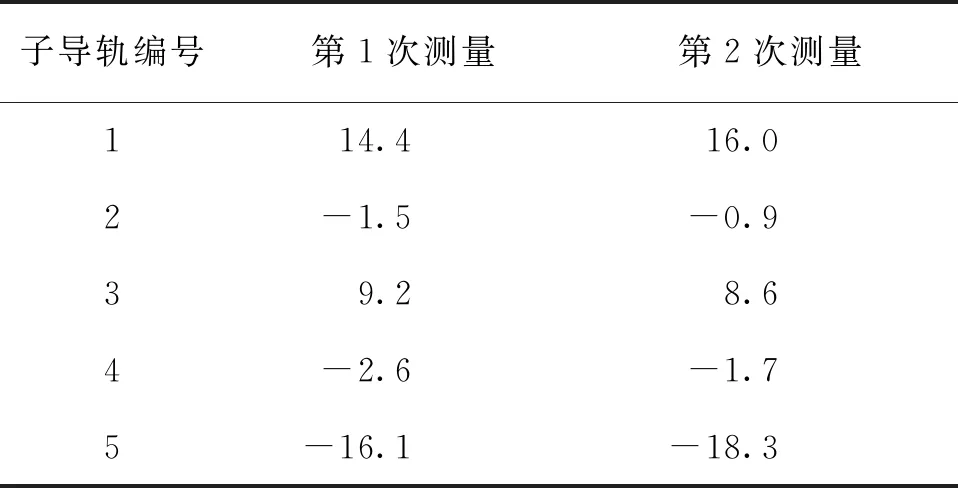
表1 单根子导轨上拟合的直线斜率值

表2 第4～7根子导轨拟合直线夹角

针对上述长导轨特性，分别依照单根子导轨斜率一致和相邻子导轨夹角稳定特性来选取不同拼接区域，以分析区域选取对于长导轨直线度坐标变换拼接精度的影响。

3.2 坐标变换拼接仿真实验

3.2.1 通过斜率进行直线度坐标变换拼接

选取了斜率一致的单根子导轨作为重叠测量区域，进行坐标变换拼接的方式，称为斜率一致区域拼接方式。

图3中第1段直线度曲线作为理想直线度曲线，最小二乘法评定得到直线度值为163.1 μm。把该曲线进行旋转平移后加入±10 μm的随机误差后得到第2段直线度曲线。选取重叠区域：导轨 12～16 m位置(位于第4根子导轨上)，进行第1段0～16 m和第2段12～30 m的直线度数据的坐标变换拼接，得到图3中斜率一致区域拼接曲线，该曲线与理想曲线偏离较远。通过加入不同随机误差的仿真实验结果表明斜率一致区域拼接得到的直线度在154.1～222.5 μm范围内分布，与理想值163.1 μm相差较大，拼接误差较大。

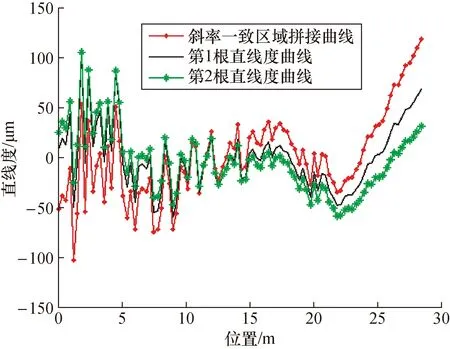
图3 在30 m范围内进行斜率一致区域拼接的仿真结果

3.2.2 通过夹角进行坐标变换拼接

选取含固定夹角的相邻子导轨作为重叠测量区域来进行坐标变换拼的方式，后文中称为夹角一致区域拼接方式。

选取3.2.1中的数据来进行夹角一致区域拼接方式的仿真实验，选取重叠区域：导轨14～18 m位置(位于第4根、第5根子导轨上)，进行坐标变换拼接，得到图4中夹角一致区域拼接方式的拼接曲线，该曲线与理想测量直线度曲线几乎重合，图中拼接直线度为159.6 μm，偏离理想直线度值 3.5 μm。多次仿真实验也表明，该拼接方式得到的直线度值偏离理想直线度值小于±4 μm。

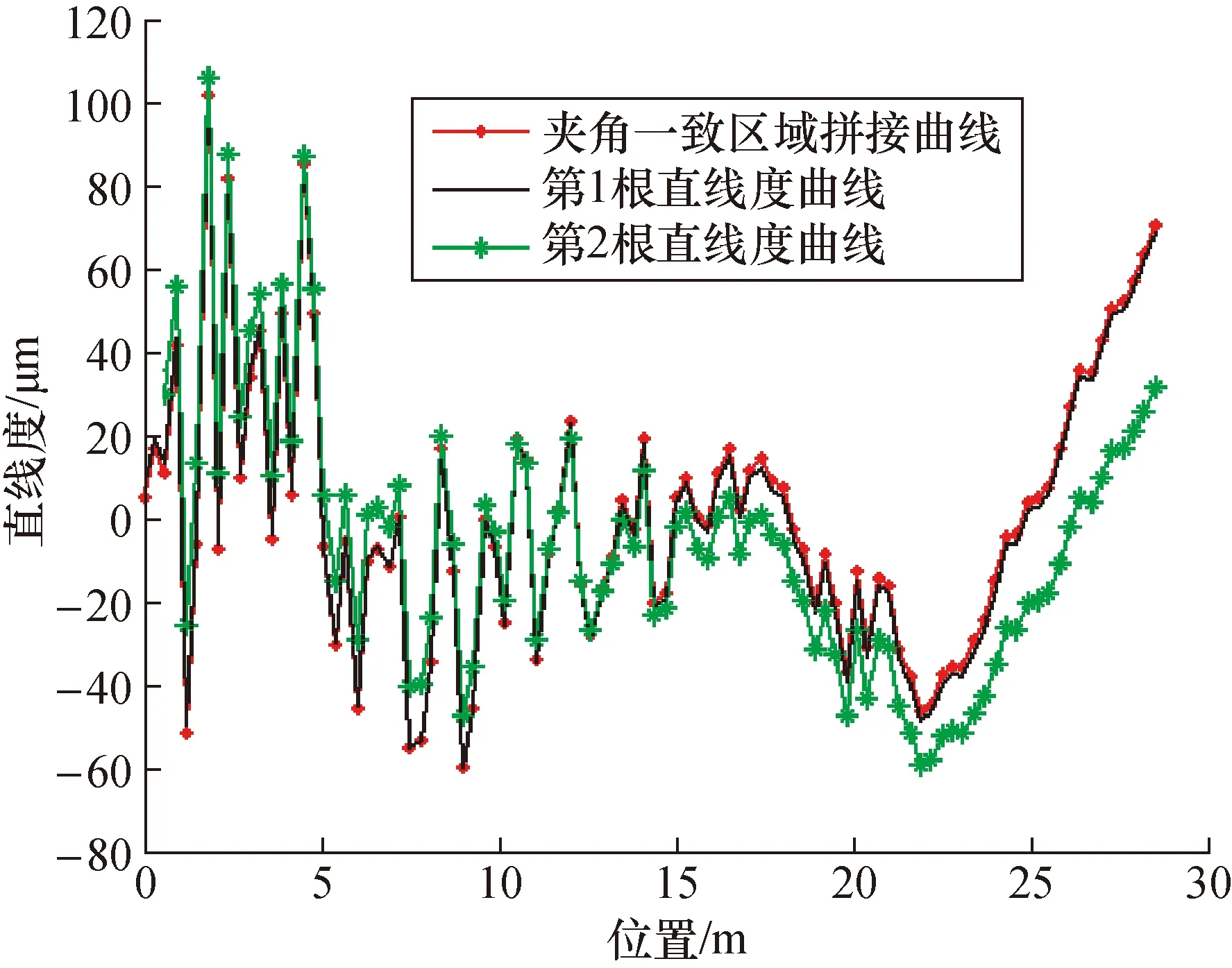
图4 在30 m范围内进行夹角一致区域拼接的仿真结果

为了验证实际与仿真结果是否一致，本文在 30 m 长导轨上进行了相关实验验证。

3.3 坐标变换拼接验证实验

3.3.1 斜率一致区域拼接方式验证实验

使用的Agilent E1733A激光干涉仪直线度测量组件，最大测量范围为30 m，在验证时，仅选取了 30 m 长导轨来进行了实验验证。

激光干涉仪以200 mm的间距分别测量了L1长度为0～20 m的导轨、L2长度为16～28 m的导轨和L长度为0～28 m的导轨直接测量直线度数据来进行斜率一致区域拼接方式进行实验验证。

图5中给出了测量重叠区域L12为16～20 m位置的斜率一致区域拼接曲线，该曲线偏离直接测量直线度曲线较远，最小二乘评定得到的拼接直线度为328.1 μm，与直接测量得的直线度164.3 μm相比相差较大。

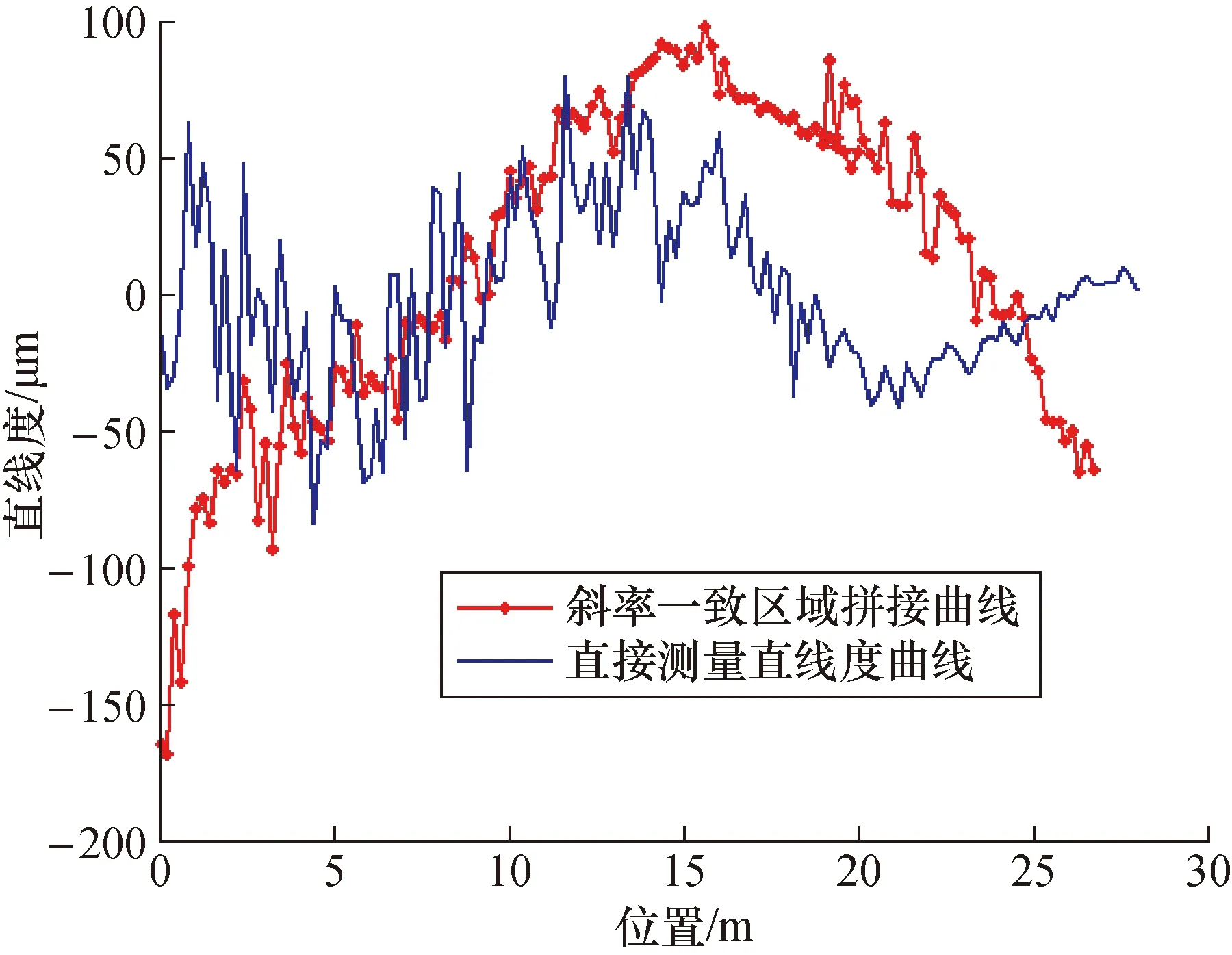
图5 在30 m范围内进行斜率一致区域拼接结果

实验中发现除了曲线偏离现象，还发现拼接曲线与直接测量曲线有时出现峰谷反向的现象见图6。分析原因，由于单根子导轨直线度较好，不同分段测量中测得的直线度值拟合直线可能斜率一致，但单点直线度数据受激光干涉仪漂动性影响重复性较差，对应测点的直线度坐标相对自导轨拟合直线恰好出现峰谷位置反置现象见图7，当选取该段数据计算转换矩阵时，旋转角度接近180°，坐标变换拼接后必然出现峰谷反置的现象。

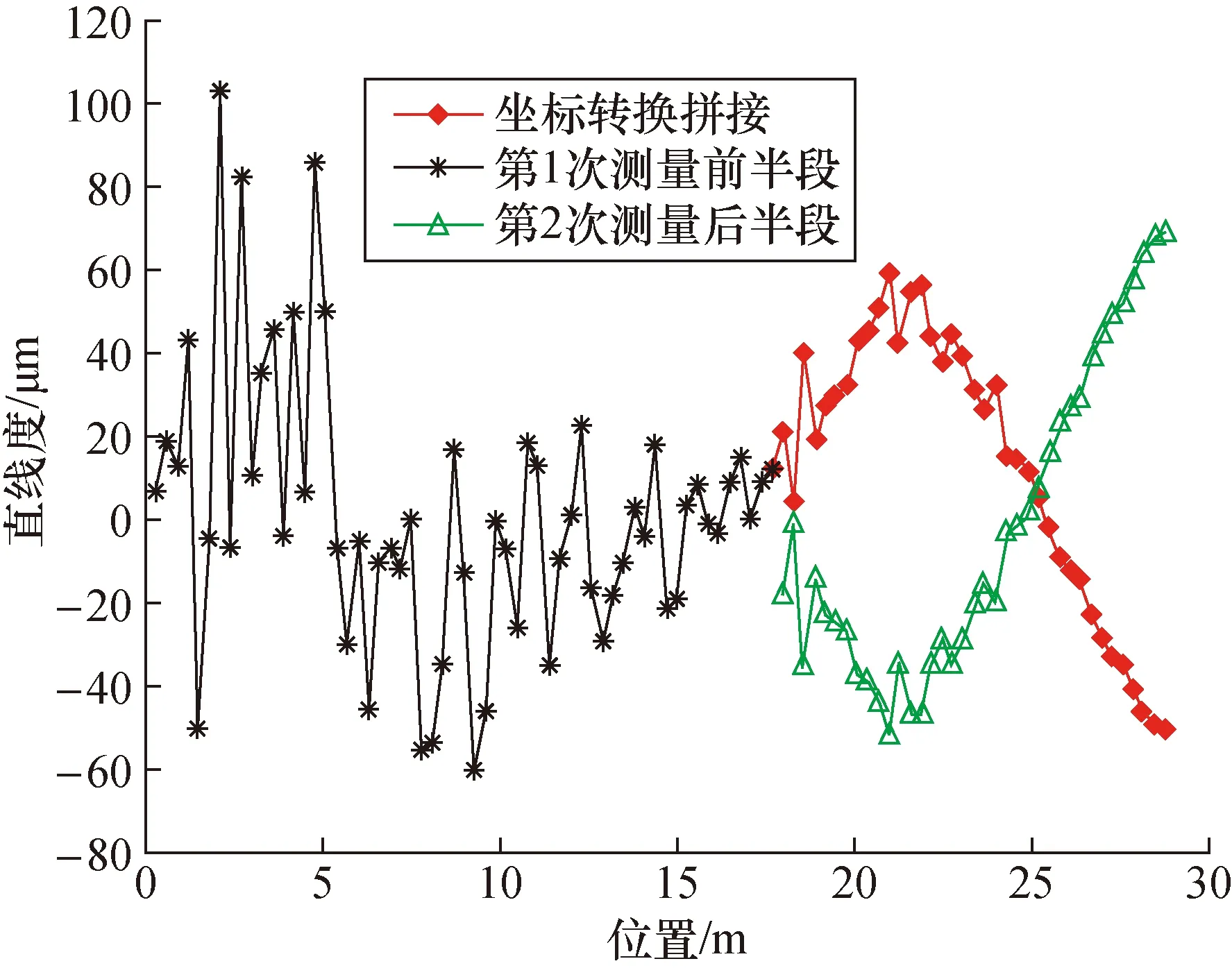
图6 斜率一致区域拼接方式导致的峰谷反向现象

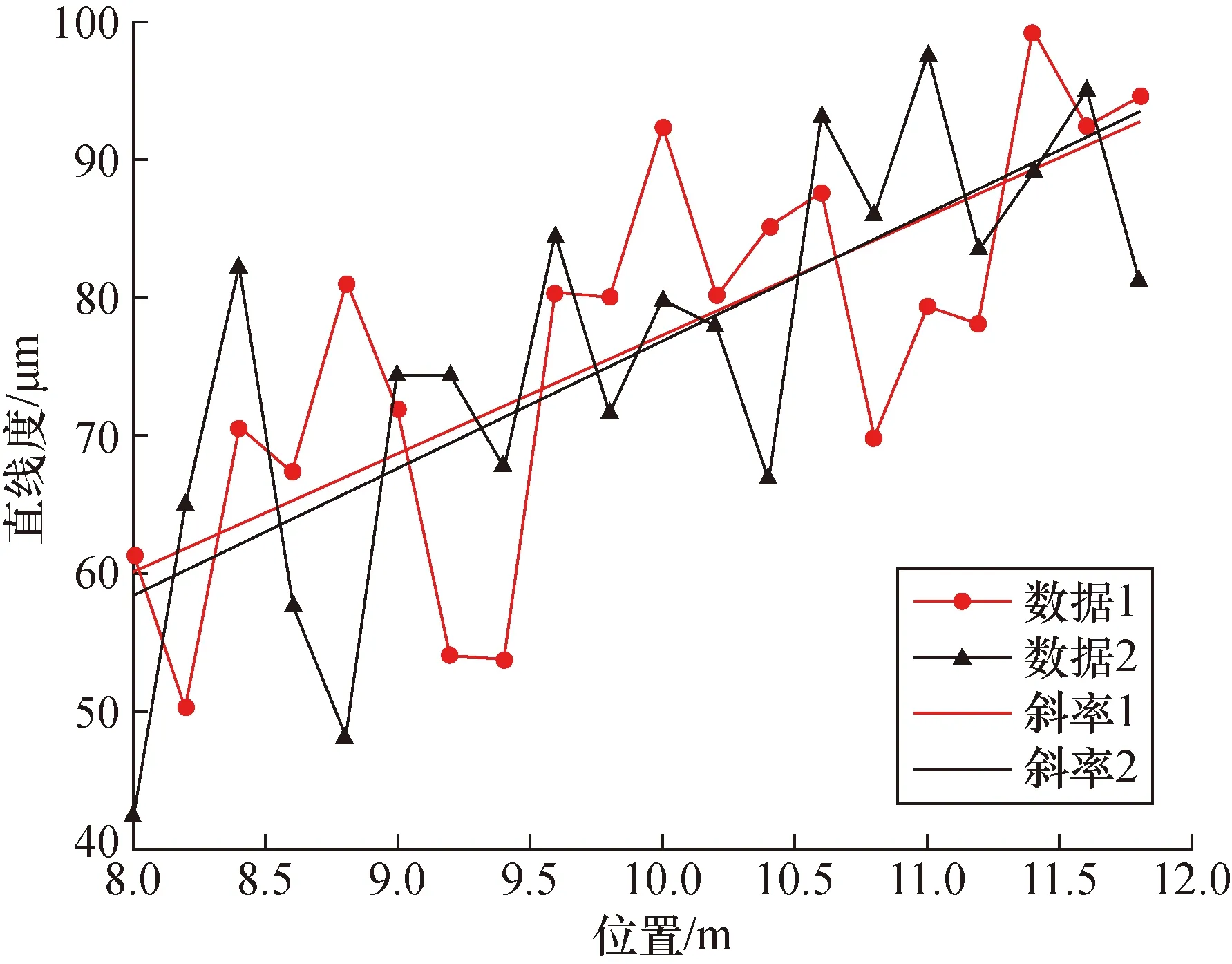
图7 单根子导轨上2次分段测量的直线度结果

验证实验结果与仿真实验结果一致，斜率一致区域拼接方式无法确保拼接精度。

3.2.2 夹角一致区域拼接方式验证实验

以200 mm的间距使用激光干涉仪分别测量了L1长度为0～20 m导轨、L2长度为12～30 m导轨和L长度为0～30 m导轨，得到几组直线度测量数据。测量重叠区域L12长度为14～18 m位置(含第 3～4根子导轨夹角位置的导轨面)，得到30 m导轨应用该方式拼接的直线度值162.6 μm，与直接测量30 m导轨得到的直线度163.4 μm相差0.8 μm，该拼接方式带入拼接误差较小。图8中夹角一致区域拼接曲线与直接测量直线度曲线走势一致，二者几乎相重叠。

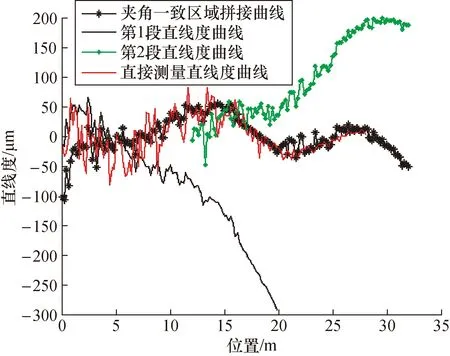
图8 在30 m范围内进行夹角一致区域拼接的验证结果

表3中给出了2种拼接方式测得的30 m导轨直线度。

表3 直线度拼接结果及偏差

从表3可知，斜率一致区域拼接方式获取的直线度值与直接测量得到的直线度值最大相差 165 μm；夹角一致区域拼接方式得到的直线度值与直接测量得到的直线度值最大相差10 μm。数据表明：前者带入的拼接误差较大；后者带入的误差则较小。图9中两种拼接曲线与实际直线度曲线的直观地体现较为直观的体现出了这一点。

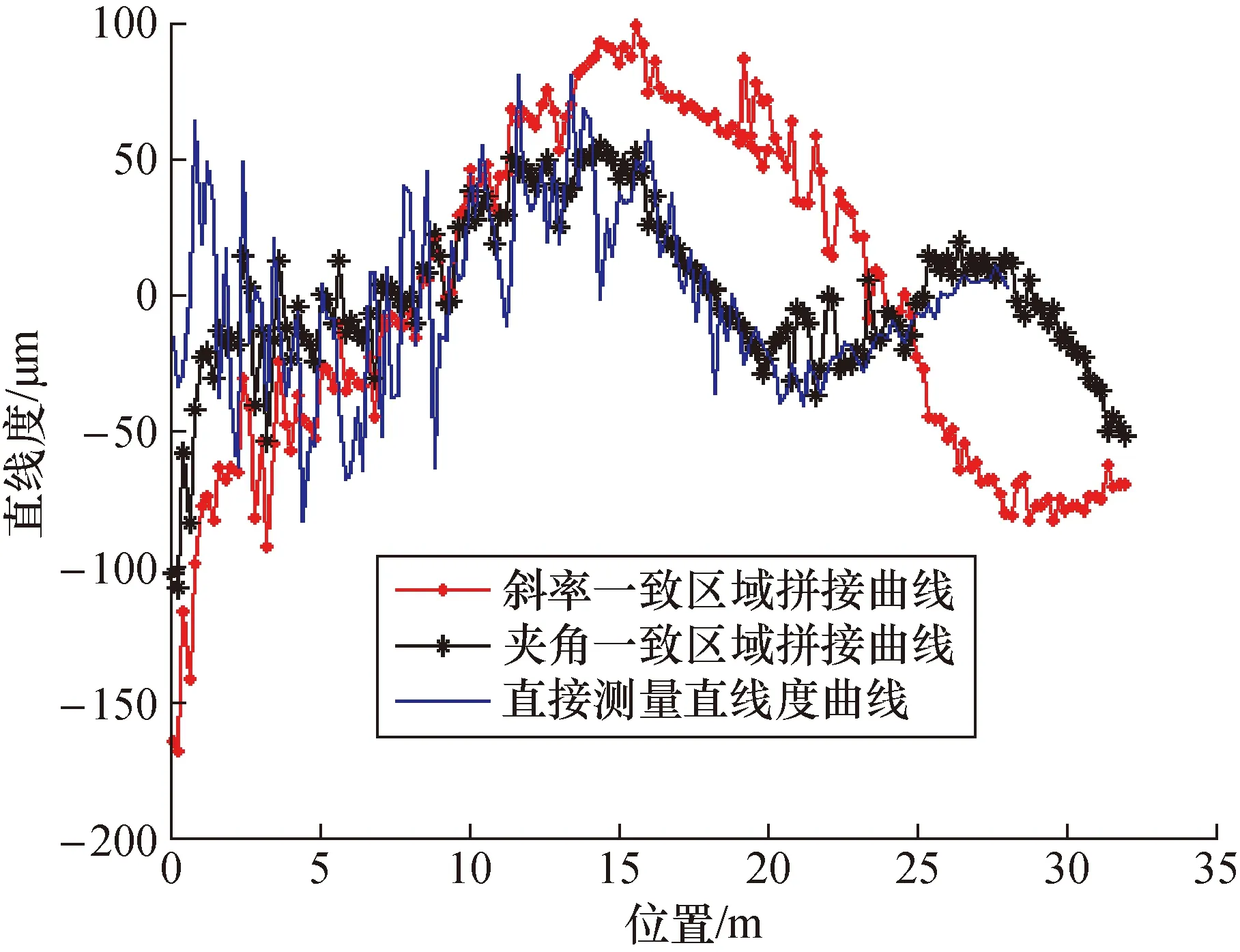
图9 斜率一直区域拼接与夹角一致拼接方式比较图

分析造成这一现象的可能原因：夹角一致区域拼接方式中选取的测量重叠区域为具有稳定夹角的相邻子导轨位置，子导轨上测得的直线度数据拟合直线夹角相对直线度数据漂动为一宏观固定特性，单点数据漂动对夹角特性影响较小，在进行坐标变换时夹角稳定使得数据漂动对转换矩阵的影响较小，有效地保证了坐标变换拼接的精度，拼接误差较小。反之，选取不含夹角的区域时，数据漂动对坐标变换矩阵影响较大，拼接误差较大。

4 坐标变换法实验验证

实验验证结果表明夹角一致区域拼接方式是一种可靠的坐标变换拼接方式，应用该拼接方式在 72 m 长导轨上分3段进行直线度测量，得到图10中直线度拼接曲线，应用最小二乘法评定得到72 m导轨的拼接直线度为0.482 mm。

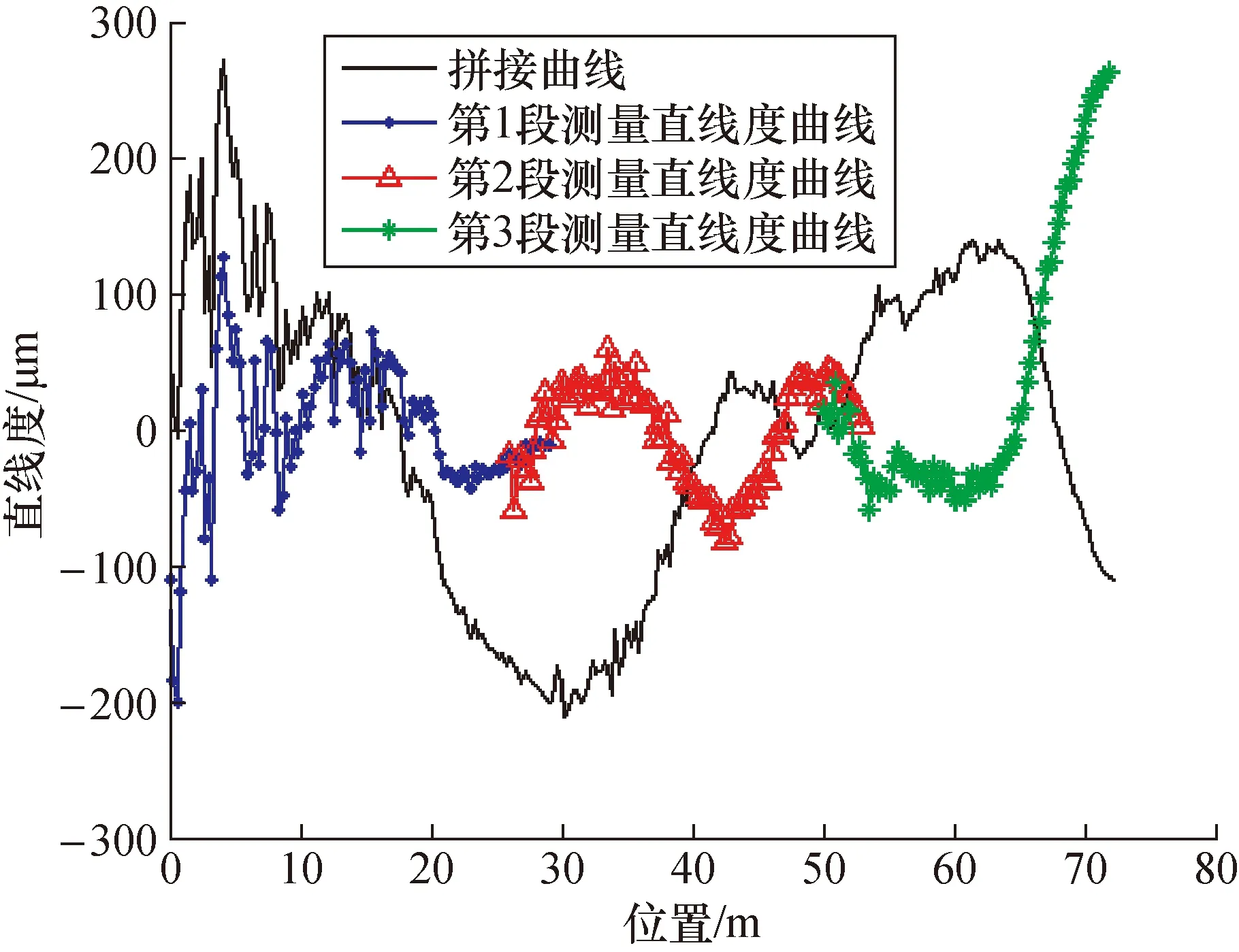
图10 长导轨72 m范围内的直线度坐标变换拼接结果

由于导轨长度远超激光干涉仪直线度测量量程，为了验证72 m范围内的拼接结果是否可靠，采用了跨距600 mm，0.01 mm/m分度电子水平仪对导轨面进行垂直方向的直线度测量。利用最小二乘法评定后得到电子水平仪测得直线度值为0.472 mm。比较两种方式测得的直线度结果，两者相差10 μm，数据较吻合，说明夹角一致拼接方式应用在长导轨直线度测量时较为可靠。

5 结 论

本文应用坐标转换方法来进行拼接，拼接过程中发现仅凭重叠区域的匹配误差和斜率一致无法较好减小拼接误差，在分析了长导轨结构特性与直线度分段测量特点后，提出了一种将拼接公共点分布在相邻2节子导轨上，用相邻两节子导轨夹角测量数据稳定的特点，来实现长导轨直线度高精度拼接的方法。

通过在长导轨30 m范围内的验证实验，对比了将拼接公共点分布在斜率一致的单根子导轨和分布在含夹角一致的相邻子导轨上的直线度测量结果，当直接测量30 m导轨直线度为163.4 μm时，单根子导轨上斜率一致区域拼接方式测得的直线度坐标转换拼接结果为140～328.1 μm，夹角一致区域拼接方式测得的直线度坐标转换拼接结果为 153～161.4 μm，夹角一致区域拼接方式在30 m内的直线度拼接误差小于10 μm。

将夹角一致区域拼接方式方法应用在72 m导轨的直线度测量上，与水平仪直接测得的直线度比较，两种测量方式得到的导轨直线度仅相差10 μm，结果表明所提出的拼接方法有利于实现长导轨直线度的高精度测量。