乡村振兴战略下定点帮扶单位绩效评价研究

陈欣蔚

华东师范大学数学科学学院 上海 201100

定点帮扶单位是乡村振兴不可或缺的重要力量。为了实现更平衡、更充分的发展，帮扶单位需要在居民收入(SR)、产业发展(CY)、居住环境(HJ)、文化教育(WJ)、基础设施(SS)这些方面进行努力。建立一个科学的绩效评估方法非常重要，将科学的评估体系纳入乡村振兴战略可以激发帮扶单位的积极主动性和农村发展的内生动力，从而提升帮扶工作的科学性、规范性、有效性。

1 相关性和差异性分析

1.1 正态性检验

为了分析2015年和2020年各项指标：SR、CY、HJ、WJ、SS以及总分之间的相关性，需要先对各项数据的正态性进行检验，以确定用何种相关系数。根据Kolmogorov-Smirnov检验可知2015年和2020年各项指标以及总分的数据都不符合正态分布，所以采用斯皮尔曼相关系数法和非参数检验法对数据组间的相关性进行分析。

1.2 Spearman相关系数分析相关性

设为样本量，为两组数据间的等级差，斯皮尔曼相关系数的计算公式为：

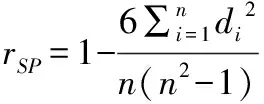
(1)

利用Matlab计算出2015年和2020年五项评价指标以及总分对应数据之间的斯皮尔曼相关系数和p值(括号中)为：0.5401(0)、0.6556(0)、0.8001(0)、0.6708(0)、0.6358(0)、0.8197(0)。

p值都为0，远小于0.05，显著性水平高，数据组间有明显关系。再观察斯皮尔曼相关系数：2015年和2020年居住环境和总分的相关系数超过0.8，相关性强；产业环境、文化教育和基础设施的相关系数落入0.6～0.7，相关性较强；居民收入的相关系数落入0.5～0.6，相对其他指标相关性一般。

同样，还可以得到2015年及2020年各指标两两之间的斯皮尔曼相关系数。以2020年的指标为纵轴，将结果用相关系数矩阵热力图表示，见图1。

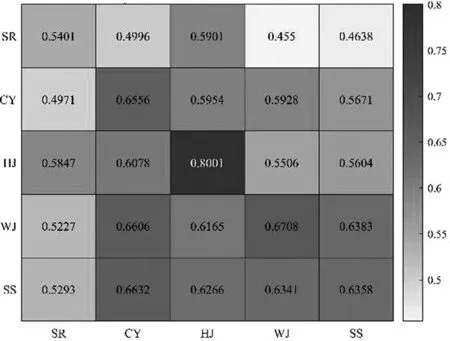
图1 斯皮尔曼相关系数矩阵热力图

斯皮尔曼系数都为正，因此当任何一个指标增长时，其他指标也会随之增长。2020年各项指标与2015年的产业发展相关性较强，2020年产业发展、居住环境、文化教育与基础设施四项指标与五年前的产业发展相关系数都在0.6以上。

1.3 非参数检验分析差异性

在显著性水平为0.05时，用Matlab对2015年和2020年五个指标以及总分对应的数据组之间作双侧符号检验，检验的p值结果见表1。

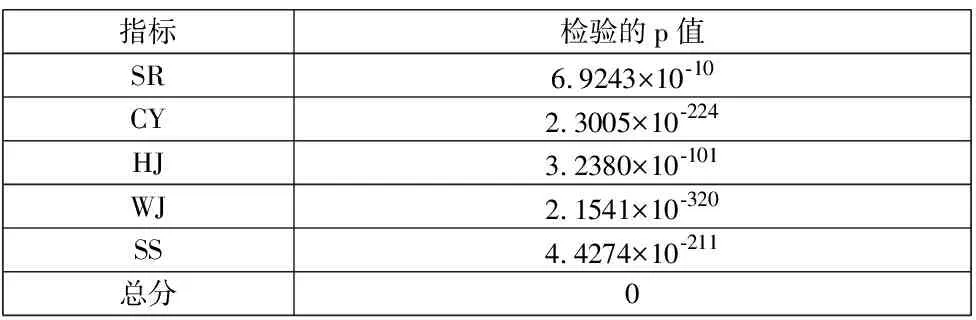
表1 2015年和2020年各对应指标的符号检验p值

检验的p值都小于0.05，因此2015年和2020年各项指标的数据之间都有显著的差异，被帮扶的村庄在居民收入、产业发展、居住环境、文化教育、基础设施五个方面都有较为显著地提升。

2 基于分位数回归的帮扶绩效分析

Roger Koenker和Gilbert Bassett在1978年提出分位数回归模型。分位数回归利用解释变量和被解释变量的条件分位数进行建模。不同于传统的经典回归模型，它的应用范围更加广泛，稳健性也更强。它能充分体现整个分布的各部分的信息，更精确地描述解释变量对被解释变量条件分布形状和变化范围的影响。

2.1 分位数回归原理

假定随机变量的概率分布函数为：

()=(≤)

(2)

对于0<<1，定义的分位数：

()={：()≥}

(3)

给定的个观测值，相对应的分位数为：

()={：()≥}

(4)

它可以等价地转化为求一个最优化问题：

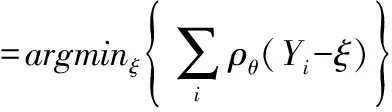
(5)

其中()=(-1(<0))是“校验函数”，其对正值和负值进行不对称的加权。

分位数回归即是对前述简单形式的扩展。若的条件分位数由个解释变量的线性组合表示，可定义的条件分位数：

(6)

其中()是与分位相关的系数向量。分位数回归参数估计量为：

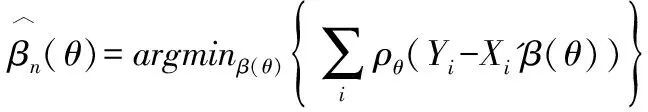
(7)

2.2 模型结果

以2020年和2015年的总分分别作为目标变量和协变量。采用SPSS进行分位数回归分析，给出在分位点为0.05、0.25、0.50、0.75、0.95的回归系数估计结果(见表2)以及分位数回归拟合图(见图2)。

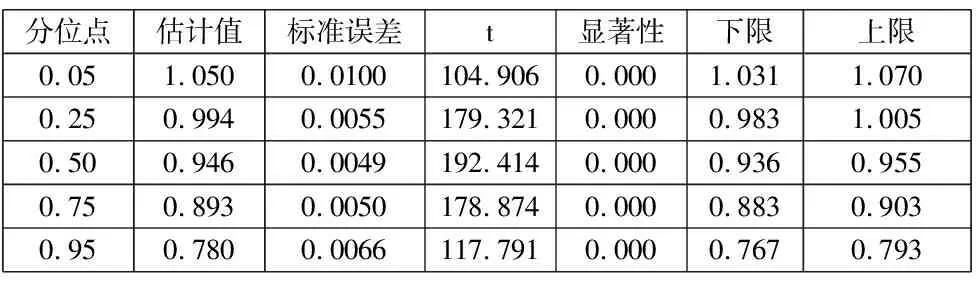
表2 不同分位点回归的斜率估计

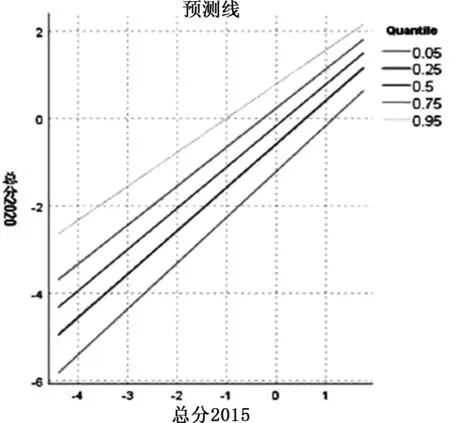
图2 分位数回归拟合图

由表2和图2可知，随着分位数的增加，截距越大，而斜率估计值越小。意味着基础薄弱的村庄，即2015年总分较低的村庄进步幅度较大。而原本情况较好，即2015年总分较高的村庄进步幅度相对没有那么显著。

3 基于TOPSIS法的村庄被帮扶成效评价

仅考虑2020年各村庄的总分并不能反映乡村振兴的成效，因为各个村庄的基础情况不同，不能忽略帮扶单位对基础较弱的村庄所做出的努力。由此还需考虑各个村庄在居民收入、产业发展、居住环境、文化教育、基础设施五个方面的提升幅度，用TOPSIS法结合熵权法给出32165个村庄的综合成绩。

TOPSIS法是一种多目标决策分析技术，根据参与评价的对象与理想解的接近程度进行打分，评价对象越逼近理想解则打分越高。

3.1 形成决策矩阵

参与评价的对象集为32165个村庄=(，，…，)，指标集为SR、CY、HJ、WJ、SS在2015年和2020年的评分之差=(，，…，)，村庄对指标的值记为(=1，2，…，32165；=1，2，3，4，5)，决策矩阵即为=()。

3.2 无量纲化决策矩阵

SR、CY、HJ、WJ、SS都是效益型指标，标准化形式为：

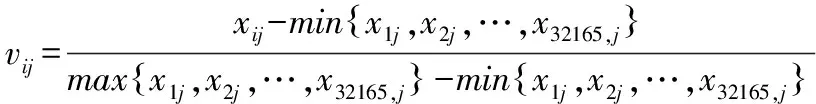
(8)

从而得到标准化决策矩阵=()。

3.3 熵权法计算5个指标的权重

专家打分法等其他赋权方式具有太大的主观随意性，采用熵权法更为客观，且具有更强的可行度、移植性和再现性。

用Matlab计算得出SR、CY、HJ、WJ、SS五个指标的权重分别为：0.2002、0.2001、0.2000、0.1998、0.2000。

3.4 构建加权决策矩阵

加权决策矩阵=()由各指标权重值与无量纲化决策矩阵相乘得到：

=·(=1，2，…，32165；=1，2，3，4，5)

(9)

w=(0.2002，0.2001，0.2000，0.1998，0.2000).

3.5 计算正理想解与负理想解

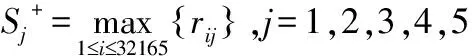
(10)

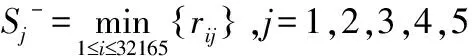
(11)

3.6 计算各村庄与正理想解和负理想解间的距离

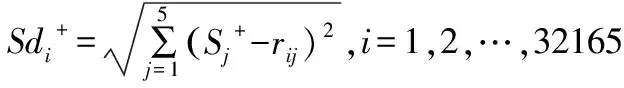
(12)

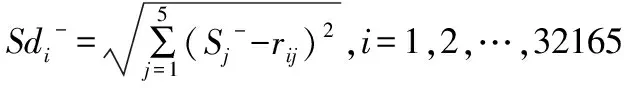
(13)

3.7 计算各方案与正理想解的相对贴近度

各村庄与正理想解的相对贴近度为：

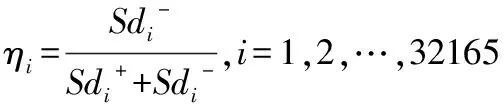
(14)

3.8 用Matlab求解模型

运用Matlab得到在该TOPSIS模型下32165个村庄的综合得分，在此列出综合成绩前十的村庄，如表3。

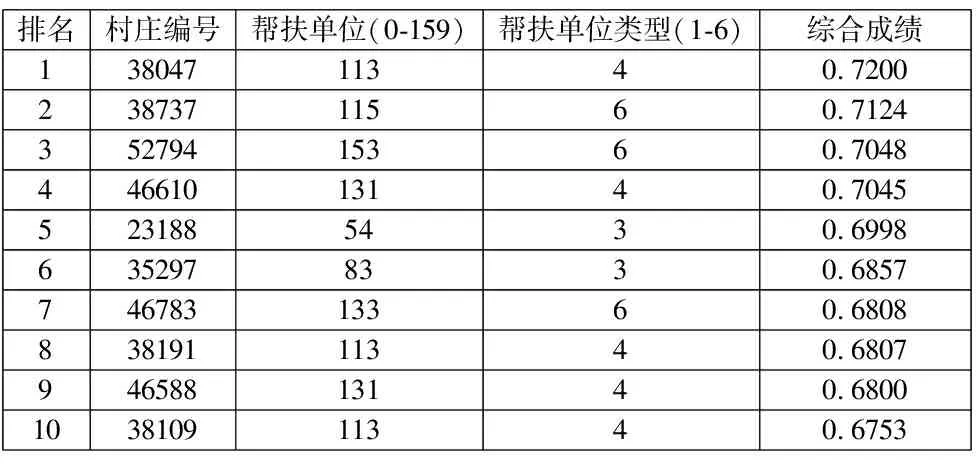
表3 综合成绩前十名的村庄

4 帮扶单位绩效评价

4.1 基于最小二乘回归排序五种类型帮扶单位

由1.2节分析已知2015年和2020年的总分数据有较强的相关性，因此以各类型帮扶单位2015年的总分作为自变量，2020年的总分作为因变量建立一元回归模型：

=+

(15)

利用Matlab进行实现，结果见表4。

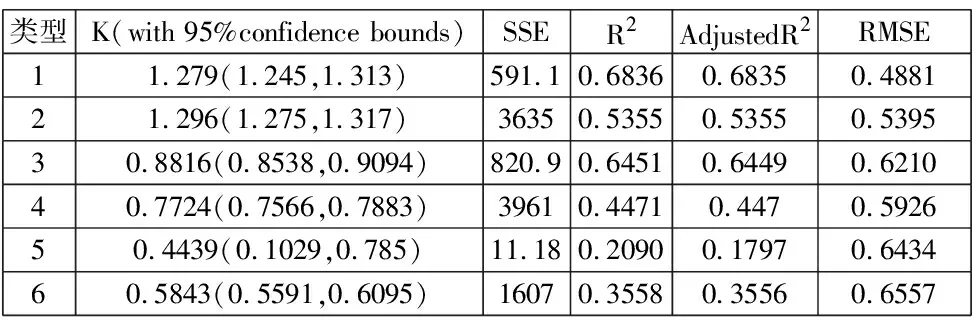
表4 一元回归结果

K值可以反映各类型的帮扶单位从2015年到2020年的总分进步幅度，由表可知：帮扶成效由大到小的帮扶单位排序依次为类型2、类型1、类型3、类型4、类型6、类型5。

4.2 基于层级聚类评价帮扶单位绩效

4.2.1 1—6类型单位帮扶绩效

用层次聚类法研究帮扶单位的成效大小以1—6类型单位对应帮扶村庄的综合评分，以及2015和2020年总分之差两组数据的平均值作为衡量各类型帮扶单位帮扶绩效的两项指标。对指标数据进行标准化变换：

(16)

采用最短距离法。首先计算样本点两两之间的欧氏距离，得到一个上(下)三角距离矩阵；然后找出距离矩阵中非零的最小元素，将相应的两类合并成为一个新类；接着用类平均法计算新类与其他类的距离，再按类间距离度量准则合并成新的一类，如此重复下去，直到所有的样本合成一类为止。

用Matlab进行实现，得到层次聚类图，如图3。

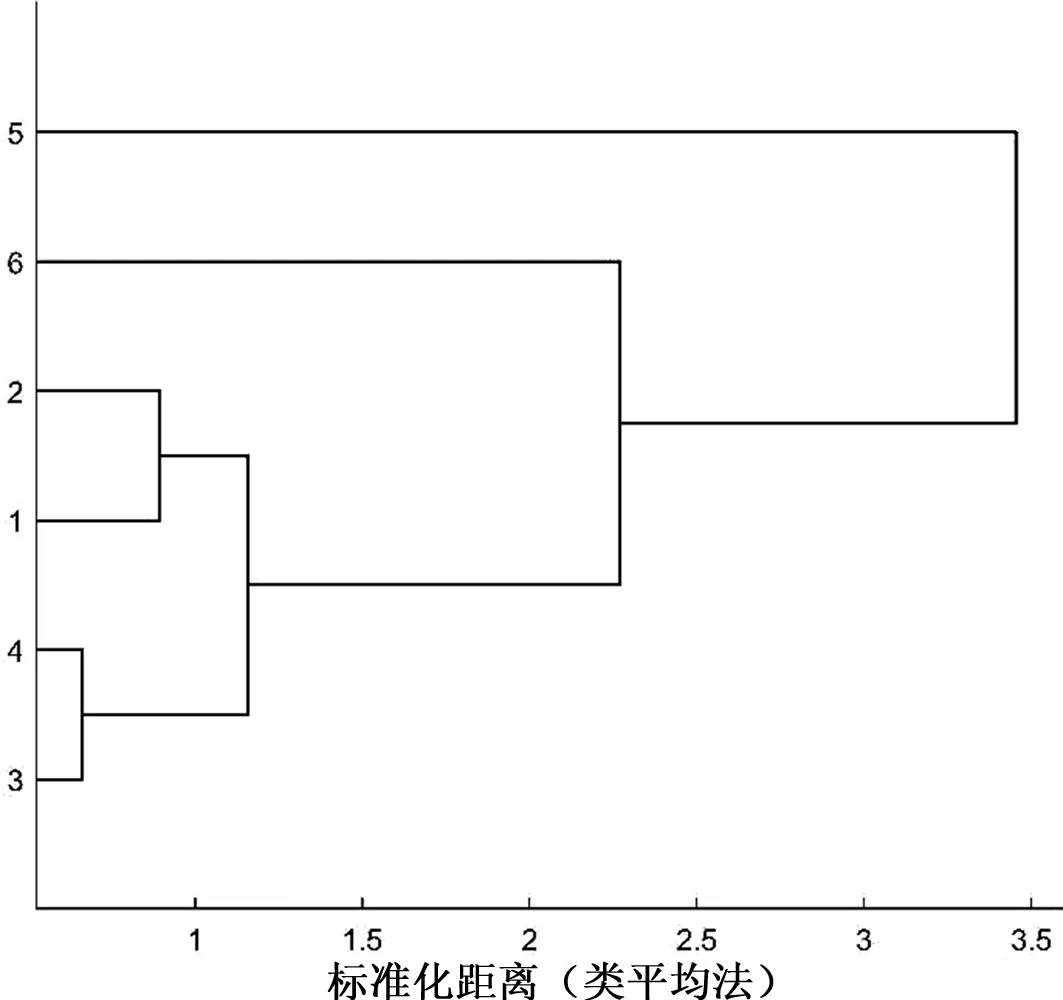
图3 1—6类型帮扶单位层次聚类图

根据以上层次聚类图可知，若确定类别数为3，则类型5和类型6的帮扶单位自成一类；类型1、类型2、类型3、类型4的帮扶单位共同组成第三类。

因此，当我们将六个类型的帮扶单位的成效划分为“优”“良”“差”三级时，结合4.1中得到的k值，可以将1—6类型单位分别定级为“优、优、优、优、差、良”。

4.2.2 1—6类型单位帮扶绩效

对0—159帮扶单位对应村庄的综合评分，以及2015和2020年总分之差两组数据各自的平均值作为衡量各类型帮扶单位帮扶绩效的两项指标，利用最短距离法层次聚类，可以对帮扶单位做出评级，见表5。

表5 帮扶单位(0-159)绩效评级表

5 结论与建议

5.1 总结

本文首先定性地对2015年和2020年各项指标及总分数据组进行分析：使用Spearman相关系数分析各组数据间的相关性，结果显示2015年和2020年各指标间都呈现正相关的关系，且各指标间的相关性总体来说较强；使用非参数检验法分析各指标和总分从2015年到2020年的差异性，发现2015年和2020年各指标的数据都有显著的差异性，帮扶成效明显。

接着定量地对帮扶单位的绩效进行评价。本文从两个角度对帮扶绩效做出评价，一个是多准则决策方法，另一个是最小二乘回归。利用TOPSIS法计算出了各村庄综合成绩；利用一元线性回归模型计算出可以反映各类型帮扶单位所帮扶村庄的进步幅度的K值，由此对1—6类型的帮扶单位的绩效进行排名。通常，国家需要对帮扶单位进行定级，建立层次聚类模型分别对1—6类型以及编号0—159的帮扶单位的帮扶成效定级为“优”“良”“差”。

5.2 建议与展望

在帮扶工作方面，各帮扶单位根据绩效评估的结果要分析工作中的优势和不足，继续扬长补短。短期眼光放在提高居民收入上；长远目光要摆在发展产业、文化教育和加大基础设施投入上，这对居民收入的提高有间接性的帮助作用。促进村庄产业振兴尤为重要，政府等单位应帮助促进农村产业的发展。一方面是农业生产方式的改变，要转型升级传统的农业生产方式，打造特色农产品，帮助滞销农产品的销售；另一方面要发展新兴产业，发掘本地特色资源，实施休闲农业和乡村旅游精品工程。产业发展的进步也能推进乡村人才振兴，减小城乡差距，促进村庄可持续发展。

在绩效评价体系构建方面，本文主要从调研所得客观数据出发得出各村庄综合成绩的算法。但是，“数量性”精准并不是最真正意义上的精准，每个村庄的特征不同，每个帮扶单位的表现形式也不同，因此不能用统一化的绩效计算公式以一概全。在实际生活中，我们的评价原则要求主观与客观相结合。在调研时还需了解村庄百姓真正的需求、对帮扶单位帮扶态度、帮扶工作的满意度以及相关领域专家的评价等主观因素。