机器学习在船舶不沉性设计策略中的应用
2022-08-20杨春蕾黄晓皓盛庆武王金宝潘常春范佘明
杨春蕾 黄晓皓 盛庆武 王金宝 潘常春 范佘明
(1. 喷水推进重点实验室 上海 200011; 2. 中国船舶及海洋工程设计研究院 上海 200011; 3. 上海市船舶工程重点实验室 上海 200011; 4. 上海交通大学 电子信息与电气工程学院 上海 200240; 5. 上海北斗导航与位置服务重点实验室 上海 200240)
0 引 言
不沉性设计策略可认为是通过主体水密舱的划分、船体开口及水密封闭装置的设计,推测出对不沉性有利和不利的条件,进而通过分析现有竞争船型或使命要求,制定有竞争力或指标先进的设计方案。在基本设计阶段,不沉性主要考虑主舱壁的影响。在不沉性理论中,静水力方法计算浮性和稳性,水动力方法计算波浪中摇摆运动、动力倾覆等,但目前由于破损船舶水动力本身的复杂性,在实用化中仍然主要是基于前种方法,或者以准静态的手段简化动态效应。船舶不沉性评估方法中,概率方法因为物理含义清晰且易于实际衡量不沉性指标而被广泛应用,针对民用船舶碰撞和触底引起的破损概率主要基于事故统计及概率分析和试验,而军用船舶破损概率基于爆炸理论和试验。
不沉性优化是制定策略的基础,在现行的优化中通常以概率不沉性指标作为约束条件,结合确定性的不沉性要素实现具体船型的优化。随着船舶不沉性法规越来越严格,机器学习模型在船舶分舱优化设计中的应用越来越重要。TURAN等以ROPAX船型为目标,以SOLAS-2009中破损生存概率A、载货量和船身自重为多目标,采用了非支配排序遗传算法进行多目标寻优,并引入了强化学习以增强模型寻优效率;CUI等针对同一问题基于JAWA平台引入了多粒子群优化,并与遗传算法进行比较说明了模型对提升寻优的影响;PAPANIKOLAOU等以Panamax邮船为目标船,以破损生存概率、经济性指标为目标,以船宽、干舷高度和水密分舱数量作为变量,采用多目标遗传算法寻优,并通过帕累托曲线建立船型要素与不沉性和经济性相关的近似关系;姜文英等应用粒子群算法等算法用于求解船舶机舱布局规划问题;林焰等在专家系统和神经网络算法基础上对油船分舱进行了研究;侯岳等基于混沌遗传算法对舰艇进行抗沉性优化,显示出了模型改进的优势。
由于实际问题的复杂性,通用的智能算法往往缺乏针对性,在基于性能的设计优化时效率低下,这相当程度上限制了实用化。粒子群算法作为一种群体智能的随机启发式算法,以简单易行、收敛速度快的优点得到广泛应用,但该算法收敛性和参数设定有赖于不断完善的理论和大量实践。尽管如此,种群数量和进化代数对实际优化效率至关重要,机器学习算法的关键控制参数也是实际应用的难点。KENNEDY等在初始的模型中对15~30只鸟的运动进行了研究,基于经验设定种群数为20,之后的研究发现20~50个之间的粒子群数具有较好的寻优表现。SHI等基于PSO-iw算法,以4种经典基准函数为测试函数,种群数量设置为20、40、80和160,探讨了增大种群数的必要性。CARLISLE等对照5类基准函数进行种群规模测试研究,种群数从5到200,在设定好相同的优化标准后,达到标准时算法即停止。研究认为30个粒子数能够获得最佳的平衡性能和速度,同时研究结果也表明了更大的种群数对二维问题寻优性能的提升有帮助。PIOTROWSKI等针对8种不同的粒子群衍化算法进行了不同种群数的测试,研究发现有些测试函数在种群数与维度弱相关,种群数在70~500之间寻优效果更佳。综合分析发现,粒子群的不同衍化算法同控制参数与实际问题的复杂性相关联,种群数与问题的维度相关联,但这种关联更偏重实践经验或特定问题。
与基准测试不同,实际问题中粒子的性能需要调用专业领域的计算模块,而计算很耗时,所以算法的控制参数需要控制计算规模,构建针对性能的专业优化框架并选择高效的优化算法和控制参数尤为重要。本文通过采用强化学习方法与演化算法结合,构建基于不沉性的分舱设计优化框架,强化学习采用Q-Learning,演化算法采用粒子群算法(particle swarm optimisation,PSO),通过对比概率不沉性算法得到的指标,来评估机器学习模型对性能的影响。
1 不沉性指标
确定性方法中,破舱进水不沉的指标规定为干舷高、初稳性高和最大稳性力臂等,但这种确定性方法指标不唯一,也难以比较2艘不同的船舶不沉性优劣。目前基于国际海上人命安全公约(safety of life at sea,SOLAS)的概率评估方法针对碰撞和触底等引起的破损评估,通过1个分舱指数即可比较1艘船最优方案和不同类型船舶的指标高低。在不同的设计阶段,优化目标往往不同,本文采用概率方法的不沉性指标。达到分舱指数为:

式中:A为满载吃水下的分舱指数;A部分压载吃水下的的分舱指数;A为轻载吃水下的分舱指数;每种分舱指数为全部破损情况所得的分舱指数总和。

式中:为舱或舱组组合;P为舱或舱组进水概率;S为舱或舱组进水后生存概率。
生存概率通过迭代求解3个载重吃水下的船舶破损后平衡水线和稳性曲线,是影响分舱指数计算效率的主要因素。进水概率计算基于破损位置和破损长度的联合密度函数的双重积分,基于民船统计数据的船舶碰撞概率分布均为线性分段函数,规范已将双重积分展开为初等函数,其效率主要受所给定舱组数以及舱室所属区域的判定,与生存概率相比占用时间较少。
2 基于强化学习的PSO算法
2.1 PSO算法
粒子群优化是一种全局优化算法,KENNEDY和EBERHART受社会学启发于1995年首次提出,之后衍化出多种算法。初始的模型为了模拟群鸟在一区域最快地搜索到食物所采取的策略,根据对环境的适应度将搜索个体指向最好区域,个体在搜索空间以一定速度飞行,由个体和群体的飞行经验动态调整。这种算法对具有较大的搜索空间、离散型多峰值特点的不沉性分舱问题具有很好的适用性。粒子群中每个粒子的空间探索受全局最优位置、个体最优位置和当前粒子速度影响,粒子的位置和速度2个物理量的具体表达为:

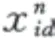
2.2 Q-Learning强化学习算法
强化学习作为最重要的机器学习方法之一,通过实时学习找到数据之间的隐藏关系,进而提高寻优效率。在有限的寻优时间代价下,能够通过与环境进行交互获得的奖赏指导行为,使智能体获得最大的奖赏。指导行为可通过领域专家经验或规律建立,可有效提升寻优的效力。具体为通过奖励找到从环境到行动的映射,可包含4个基本模型:策略、奖励函数、价值函数,以及环境模型。Q-Learning作为应用最为广泛的强化学习算法,由WATKINS于1989年提出,是一种无模型强化学习。环境对Q-Learning的要求是灵活的,对离散环境的工程问题适用性强,因此本文采用此方法。智能体的行动以矩阵元素体现,通过训练更新并指导下一轮行动,可表达为:
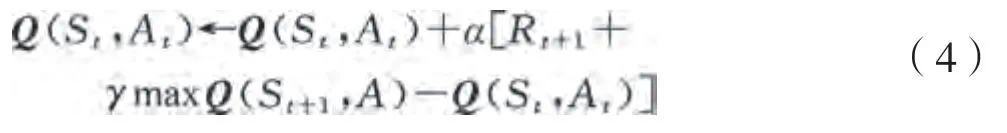
式中:S为当前状态;A为当前状态下采取的行动;S为新一轮状态;R为下一轮行动奖励;为控制收敛的学习率;为折减因子。
2.3 混合算法
强化学习的目的是通过训练粒子搜索控制参数(、、)提高优化能力和收敛性,构成本文采用的QL-PSO混合算法。强化学习的要素对象见表1。
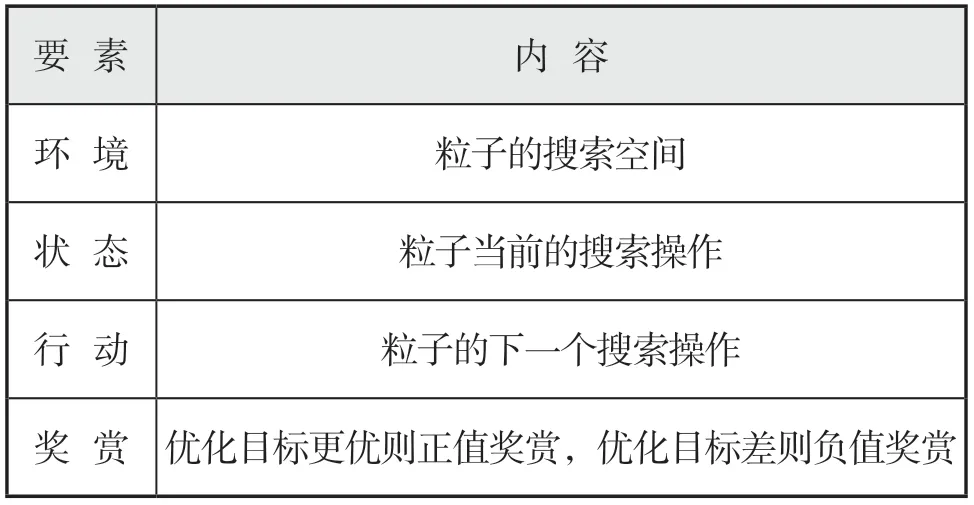
表1 强化学习要素内容
根据每个粒子的矩阵值控制粒子群探索空间,通过更新速度与位置计算出目标函数,并得到奖赏策略,最后更新矩阵。表1中3种状态,探索操作为整个优化过程的初始阶段,值较大且较占优。收敛操作为整个优化过程的结束阶段,值较小且较占优。低跳阶段介于两阶段之间。
3 结果讨论
3.1 程序架构
以图1所示的远望船为目标船型。

图1 远望船
选取主横舱壁、纵向舱壁和垂向舱壁作为优化变量,并基于参数化建模技术和静水力计算工具实现基于概率方法的不沉性计算。机器学习算法基于Python平台,模块为自主开发,功能开发灵活且具有针对性,界面示意图如图2所示。
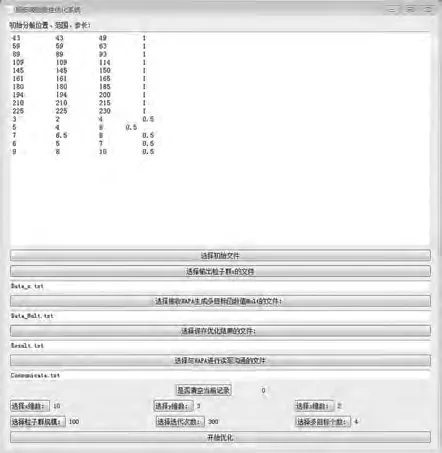
图2 不沉性机器学习程序界面
用户界面包括船舶参数、初始分舱、范围、步长和目标函数个数,算法参数包括粒子群的规模、迭代次数,数据参数为专业模块通讯过程与结果数据,集成的专业模块为可参数化的分舱设计和不沉性计算的自主开发程序,也可为商业软件。机器学习模块与船舶不沉性设计专业模块通过文本方式进行数据传输,设置详细的通讯机制以避免模块读写冲突,具体为:
(1)机器学习模块提供粒子群信息以及一组 分舱布置方案;
(2)专业模块提供粒子群对应不沉性指数 矩阵。
研究中,分舱布置方案为简化布置方案,意在为初始设计阶段提供不沉性分舱策略性建议。有关分舱简化方法的合理性,RAVN等以3艘汽车船为例进行了2种不同程度的简化建模并与实际模型的计算对比。研究表明,考虑合理简化不显著影响不沉性指标。在初期的优化中,不沉性的变化趋势对设计策略更为有意义,简化对指标的趋势影响较小,因此本文计算采用简化建模,局部大舱和主要甲板位置保持固定。
3.2 计算结果分析
初始值的选取对最优结果和效率影响较大,本文采用给定1个初始粒子,第2代开始由1个粒子随机生成给定种子数的粒子。由于每代粒子之间有位置重叠,且当代粒子也有可能与前代的粒子位置重叠,程序基于信息查重以避免专业模块重复计算,体现了粒子信息的可继承性,大大提高了效率。
在粒子初始值相同、演化代数设置相同时,研究种子数对优化能力的影响,图3为PSO算法的全局最优时历结果,图4为QL-PSO算法的全局最优时历结果。
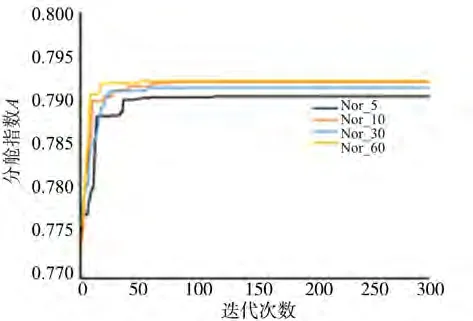
图3 PSO算法的全局最优时历
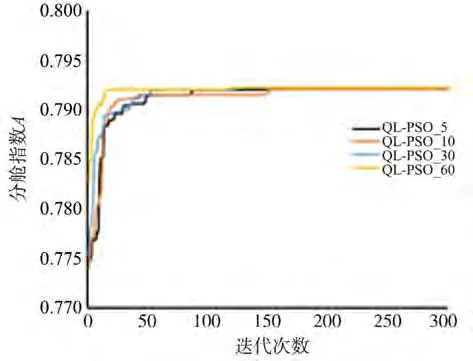
图4 QL-PSO算法的全局最优时历
图5为相同种群数时不同算法的全局最优时历曲线。时历曲线表明了大的种群数时全局最优曲线的拐点更早出现,同时不同算法的时历曲线也表明混合算法的全局最优曲线拐点更早出现。

图5 相同种群数时不同算法的全局最优时历
图6为选取了种群数为30时第1个粒子在不同算法时的迭代历程,数据显示:PSO算法在0~150步时波动较大,之后的迭代波动很小;QL-PSO算法在0~40步时波动较大,但在200步左右和之后的迭代中出现明显的波动。在300步迭代中,PSO算法中粒子不相同位置数207个,少于QL-PSO中的230个,显示出了强化学习模型增强了粒子的发散,从而提升了粒子群的多样性。在给定种群进化数时,QL-PSO算法中粒子历经了更多的不同位置导致总体计算效率低,但在相同的指标标准时,QL-PSO方法却能经历更少的位置,即迭代代数更少。对实际数据采用对数拟合,2种趋势线的决定系数平方值中,PSO方法为0.697 6,较QL-PSO方法的0.333 3更接近1,反映出实际值与趋势线拟合程度更高,数据集中度更高。
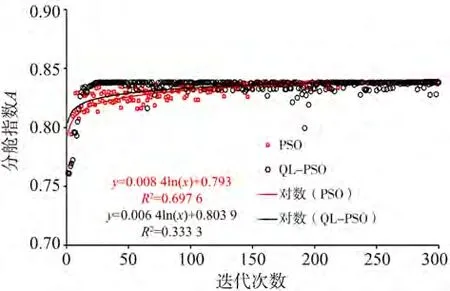
图6 某粒子迭代历程
下页图7为第1横舱壁位置对分舱指数的影响,图中显示了第1横舱壁靠后更有利于不沉性的指标。
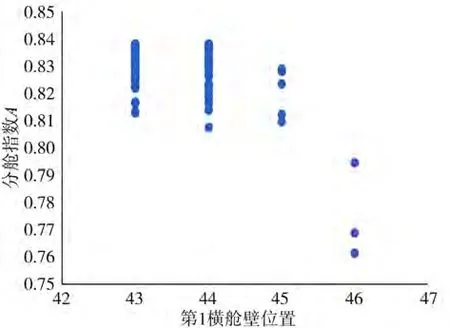
图7 舱壁位置随分舱指数变化
4 结 论
本文针对船舶不沉性分舱优化问题,应用不同的粒子群算法到不沉性分舱全局和局部优化问题中,研究结论及讨论为:
(1)基于强化学习的PSO混合算法与标准PSO算法对比计算表明,混合算法有助于加速收敛,且能够更快达到全局;
(2)本文计算采用简化的分舱模型以提高计算效率,适用于在设计初期阶段为不沉性分舱提供全局性参数优化策略,为后续多阶段局部不沉性分舱策略提供基础。
