粒子群算法在镁合金3C 产品覆盖件冲压成形优化中的应用

镁合金3C 产品覆盖件冲压成形是材料非线性、几何非线性和边界非线性的成形过程，极易出现冲压开裂和起皱等缺陷，冲压成形工艺的制定及优化成本高、难度大，一直是镁合金3C 产品塑性成形领域的研究热点。

本文基于有限元数值模拟和粒子群优化算法的冲压成形优化方法，引入了非线性自变惯性权值和非线性自变加速因子，对多目标粒子群优化算法进行针对性改进(Improved Particle Swarm Optimization，IPSO)，构建了工艺参数与成形质量之间的数学分析模型，利用IPSO 粒子群优化算法求解数学分析模型，获得了最优冲压成形工艺。

改进粒子群优化算法

在非线性大变形的覆盖件冲压成形中，由于非线性约束的问题，易导致粒子群优化计算时，求解出局部最优而全局空间非劣的次优解。为了解决此类非最优问题，本文在传统的多目标粒子群优化算法中，针对性地引入了非线性自变惯性权值和非线性自变加速因子。

非线性自变惯性权值

在多目标粒子群优化算法中，惯性权值ω 是描述各粒子对现速度继承的阈值，是权衡各粒子全局空间搜索能力和局部空间搜索能力的重要平衡参数。当惯性权值ω 较小时，多目标粒子群优化算法的局部空间搜索能力变强；当惯性权值ω 较大时，多目标粒子群优化算法的全局空间搜索能力变强。

在不同的计算迭代中，采用非线性自变惯性权值ω

要比采用固定惯性权值的寻优效果更好。因此，本文根据非线性大变形覆盖件冲压成形特性，将非线性自变惯性权值ω

与目标函数值相挂钩，在每次迭代计算中，非线性自变惯性权值ω

都会随着目标函数值的不同而自动发生改变，其公式如(1)所示。

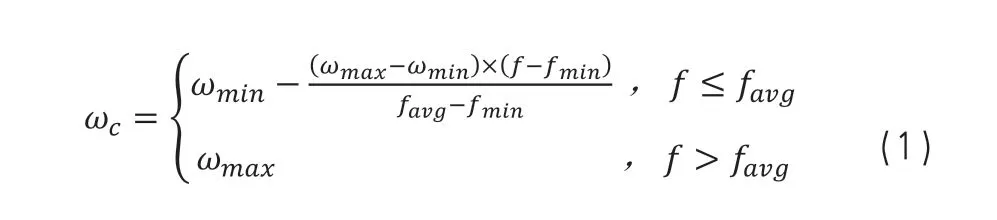
在成形极限图FLD 中，距离安全成形区域越远的单元开裂和起皱的危险程度越大，本文以安全距离的指数为权重，构造开裂目标函数R

和起皱目标函数W

如(5)、(6)所示。

非线性自变加速因子

在多目标粒子群优化算法中，加速因子σ

和σ

是各粒子向群体中优秀粒子靠近的调节因子。使用每次迭代计算中不断变化的加速因子σ

和σ

的初始值和终了值，而非线性自变的加速因子σ

(t)和σ

(t)，可使各粒子在优化过程中不断增强全局空间搜索能力，最终提升最优解的捕获能力，其公式如(2)所示。

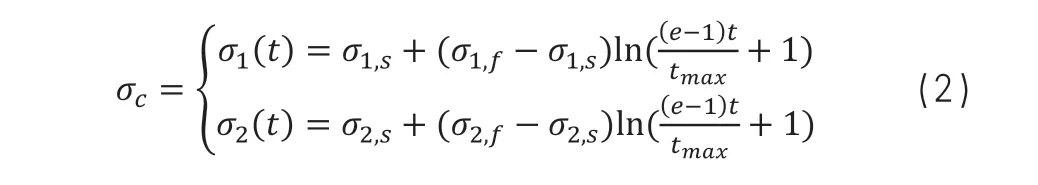
沙沟沟域形态呈不规则的的“V”形，右侧反向坡坡度较陡，左侧顺向坡与岩层倾角基本一致，冲沟流域长度为1.5km，宽度为0.35～0.45km，汇水面积为0.6km2。区域内最高点位于北东侧，高程为1150m，最低点位于柏枝溪沟口，高程为700m，相对高差450m。主沟平均纵坡降为300‰，属于易发泥石流的沟床比降范围[3]。

对板材温度T

、凸模温度T

、压边力F 和冲压速度S 等4 个连续的设计变量，以正交试验均匀选取64 组样本进行有限元数值模拟计算，其中48 组作为训练样本，16 组作为测试样本，将试验得到的主应变ε

和次应变ε

带入公式(3)～公式(6)，即可求解出相应的目标函数值。

4.1.2 分析：从芯片日志可以看到，芯片在覆盖等级0接入时，最低发送功率-7db大于协议规定的-40dbm,对邻区干扰也有影响。

构建算例数学分析模型

本文以某镁合金3C 产品覆盖件的冲压成形为研究对象，该覆盖件的有限元数值模拟三维模型见图1。

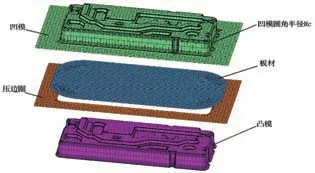
设定分析模型参数

镁合金是世界上最轻的金属结构材料，是3C 产品覆盖件的理想选材。室温下镁合金的塑性变形能力差，冲压成形时易发生开裂和起皱缺陷；随着变形温度的升高，镁合金的塑性变形能力增强，特别是在复杂温变条件下，冲压成形性能更好。因此，本文选用板材温度T

和凸模温度T

作为首要设计变量，再选择对冲压成形影响较大的压边力F 和冲压速度S 作为次要设计变量，其他影响因素以设计常量处理。

冲压板材为AZ31B 镁合金，材料性能参数为：板材厚度τ=0.9mm，弹性模量E=44.8GPa，泊松比v=0.35，热膨胀系数α=2.5×10

℃

，摩擦系数μ=0.125，板材尺寸为140mm×75mm，板材圆角r=10mm。冲压模具设定为刚体，凸凹模间隙Z=0.99mm，凸模圆角半径R

=3.5mm，凹模直壁圆角半径R

=4.2mm，拉延筋阻力R=230N/mm。

建构目标函数

根据成形极限图FLD(图2)，定义开裂和起皱曲线如(3)、(4)所示。

式中，n 为板材单元总数；ε

为主应变；ε

为次应变。

冲压成形的缺陷主要有开裂、起皱和成形不足3类。在镁合金3C 产品覆盖件冲压成形中，成形不足缺陷的影响很小，因此，本文主要考虑开裂缺陷和起皱缺陷。

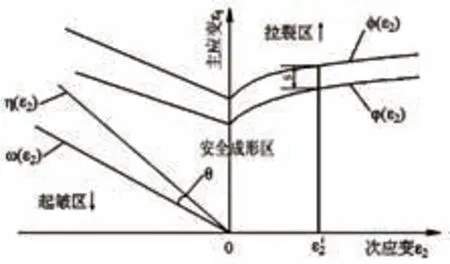
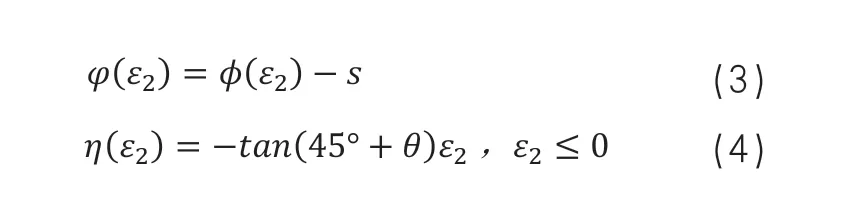
式中，

(ε

)为拉裂极限曲线；

(ε

)为拉裂安全曲线；η(ε

)为起皱安全曲线；ε

为次应变；s 为拉裂安全度；θ 为起皱安全度。

式中，ω

为惯性权值ω 的最大值；ω

为惯性权值ω 的最小值；f 为各粒子现速度目标函数值；f

为各粒子目标平均值；f

为各粒子目标最小值；

式中，σ

为σ

的初始值，σ

为σ

的终了值；σ

为σ

的初始值，σ

为σ

的终了值；t 为迭代次数，t

为最大迭代次数。

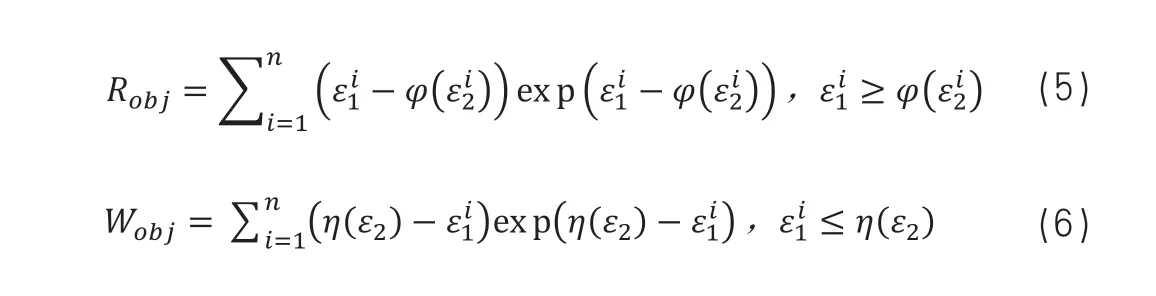
自动焊接设备选用林肯焊接电源R350和某公司的焊接小车系统。焊接电源具备平特性电流及脉冲电流MIG/MAG焊功能，具有控制精度高，稳定性好，性能卓越等特点。同时，焊接电流、电弧电压及焊接速度等参数可以数字显示并连续可调。焊接小车采用有轨道式，能够满足平、横、立、仰四个位置的平稳焊接。

构建优化模型

在镁合金3C 产品覆盖件的冲压成形中，构建优化数学模型如(7)所示。

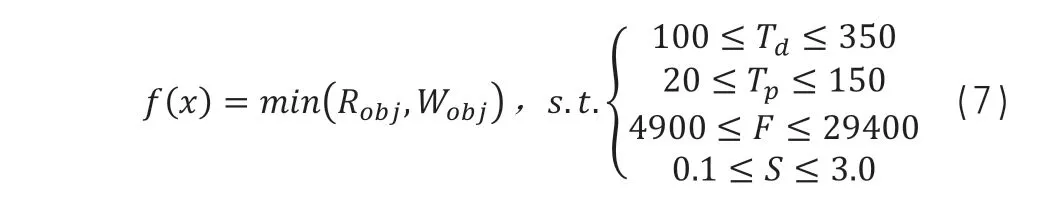
在经费方面，由于社工组织提供的服务基本上是以无偿或低偿为主，为了保障组织的日常运行，社工组织在硬件设施的购买、社工薪酬、办公经费等几乎都依靠政府的财政支持。广州市政府在颁布《关于加快街道家庭综合服务中心建设的实施办法》明确提出“政府购买社会服务资金要纳入常态化财政预算。街道家庭综合服务中心购买社会服务及评估经费按照市、区(县级市)财政分担比例共同资助。广州市财政将按每个家庭综合服务中心每年200万元的项目购买经费预算来预留市的分担比例预算④。”由此看来，街道作为政府购买服务的监管方，为社工开展服务提供了场地方面的资源支持，而秉承不以营利为目的的社工组织也对政府的场地存在依赖。

优化计算与结果分析

优化计算

设定粒子种群大小为35；终止迭代次数t=200；设定最大惯性权值ω

=1.2，最小惯性权值ω

=0.6；加速因子σ

的初始值σ

=3，加速因子σ

的初始值σ

=0.5；加速因子σ

的终了值σ

=0.5，加速因子σ

的终了值σ

=3。

婚前一见面就亲嘴，婚后一见面就斗嘴；婚前生活妙不可言，婚后日子苦不堪言；婚前谎话都是情话，婚后情话都是废话；婚前的男人很幽默，婚后的男人很沉默；婚前做什么都浪漫，婚后做什么都浪费；婚前情话绵绵，婚后谎话连连；婚前爱情是神话，婚后爱情是笑话！

利用IPSO 粒子群算法，求得二次多项式响应面数学模型如下：

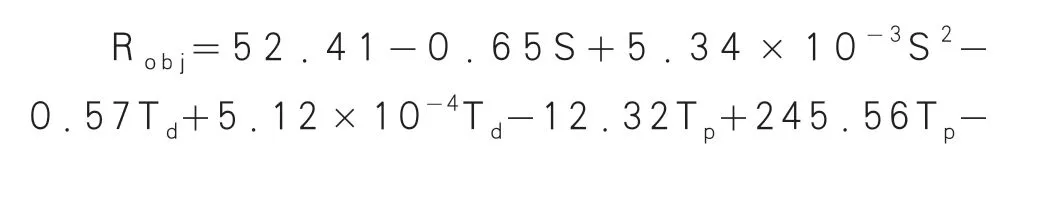
结果分析

经过IPSO 粒子群算法优化计算后，运用最小距离选解法，将求得的开裂目标函数R

值和起皱目标函数W

值在空间解集中选取距离最短的最优粒子P

。P

对应的工艺参数为：板材温度T

=271.33℃，凸模温度T

=45.61℃，压边力F=20201.17N，冲压速度S=1.70mm/s。

将IPSO 计算的最优粒子P

的工艺参数输入Dynaform 有限元软件进行数值模拟计算，得到的成形极限图FLD 如图3 所示。从图中可知，镁合金3C 产品覆盖件的开裂和起皱得到了有效地控制，未产生开裂和严重起皱等缺陷，覆盖件冲压成形安全且充分。

实施国土资源所巡察“五个三”行动计划 整体提升基层国土资源一线工作水平（殷金兰） ..........................3-12

结论

本文成功将非线性自变惯性权值和非线性自变加速因子引入到多目标粒子群优化算法中，构建了工艺参数与成形质量之间的数学分析模型。在此基础上，将IPSO 粒子群算法应用于镁合金3C 产品覆盖件冲压成形后，取得了满意的效果。实例证明，IPSO粒子群算法能有效优化镁合金3C 产品覆盖件冲压成形工艺，显著提升复杂温变条件下覆盖件的冲压成形质量。