基于Piecewise算法的反正切运算器的设计*

龙科莅，汪 东，陈 虎，李旭军

(1.湘潭大学物理与光电工程学院，湖南 湘潭 411105；2.湖南毂梁微电子有限公司，湖南 长沙 410000)

1 引言

在科学计算、图像处理和数字信号处理等应用领域中，反正切运算都是常用的基础操作。由于软件方法的运算速度通常较慢，不能满足应用的实时性要求，需要设计专用于反正切运算的硬件电路，即反正切运算器。

在设计反正切运算器的过程中，如何在运算器的精度、速度和硬件成本三者之间进行权衡是一个关键问题。为了解决这一问题，在以往的工作中提出了3类方法，即简单查表法[1,2]、数字迭代法[3 - 6]和Piecewise算法[7 - 13]。

简单查表法是指根据输入从预先存储的数据表中查找出对应的运算结果输出。这种方法所需的表空间会随所要求的运算结果精度的提高而呈指数增长。为了压缩表空间，一类通过加法链接多个查找表从而获得运算结果的多部表法[1,2]应运而生，但这种方法若用于精度较高的运算，所需的表空间仍然较大。

CORDIC(COordinate Rotation DIgital Computer)算法是典型的数字迭代法，其硬件耗费较小,每次迭代只能获得结果的一个数位，因此延时较高[3,4]。为了降低运算延时，以增加运算电路的复杂性为代价，Kebbati等人[5]开发了该算法的并行性；Lakshmi等人[6]则提高了CORDIC算法的运算基数，使得一次迭代能获得结果的更多数位。

Piecewise算法将运算区域划分成有限数量的子区间，在每一个子区间内对原函数用多项式逼近以获得误差允许范围内的运算结果。所有子区间内用于逼近的多项式形式相同，仅根据子区间的不同来选取不同系数[7 - 9]。因此，子区间的数量直接决定了所需存储的系数数量。另外，根据所划分的子区间大小是否相同，又分为均匀[10,11]与非均匀[12,13]2种子区间划分方式。非均匀划分的方式更加灵活，往往能极大地减少子区间数量，从而压缩系数表空间。Piecewise算法适合采用流水线的实现方式，且可通过调整分段子区间数量等方式来实现硬件成本与延时的平衡，具备较大的灵活性。

本文设计的反正切运算器输出结果与准确结果之间的允许误差为1 ulp (unit in the last place，最后位置单位)，足以满足诸多实际应用的要求。然而，在这种精度条件下，运算器的输出可能会随输入的递增在可允许的误差范围内变化，而不是像原函数那样随输入的增加而逐步递增，因此会引发单调性违例。在图像处理等应用中，运算结果保持与原函数一致的单调性是十分重要的，比如纹理映射对于反正切运算的输出是否具备与原函数相一致的单调性十分敏感[14]。为了消除Piecewise算法引发的单调性违例，文献[1]提出了一种通过调节斜率(Appropriate Slopes)和表初始值TIV(Table of Initial Values)来改善输出的单调性方法；文献[14]则通过测试所有输出获得引发单调违例的输入范围，并以此对系数表进行经验式的调整，以改善运算的单调性。

Table 1 Subintervals obtained by two-level hierarchical segmentation表1 二级分层分段获得的子区间

Table 2 Number of subintervals obstained by different segmentation methods表2 不同分段方法产生的子区间数量

Table 3 Signal width obtained by static analysis表3 静态分析获得的信号位宽

Table 4 Signal width obtained by dynamic analysis表4 动态分析获得的信号位宽

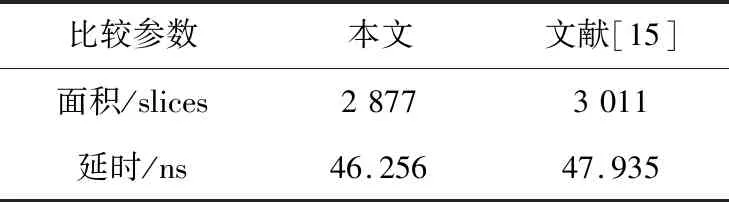
Table 5 Comparison results based on programmable logic表5 仅基于可编程逻辑的比较结果

本文基于Piecewise算法，设计了一种输入输出都符合IEEE-754单精度标准的浮点反正切运算器，同时，使用二级分层分段方法进行非均匀分段，以压缩系数表空间。另外，通过控制单调性违例区域的尺度使其小于该区域内输入数的1 ulp大小，从而消除Piecewise逼近法带来的单调性违例。此外，通过误差分配以及对误差与位宽之间关系的分析完成了位宽设计，并通过有限范围内的动态分析进行了位宽优化。

2 算法与架构

本文旨在完成如式(1)所示的反正切运算。运算的输入输出信号皆为IEEE-754标准的单精度浮点数。

(1)

2.1 多项式逼近

Piecewise算法往往在每个分段子区间内采用一阶、二阶或三阶多项式对目标函数进行可允许误差范围内的逼近。由于“龙格效应”，即逼近误差不随多项式的阶数增加而一致减小，更高阶的多项式很少被采用。根据文献[8]可知，对于单精度浮点运算，在硬件成本与延时之间进行权衡，相较于需要一个较大系数表的Piecewise一阶多项式逼近或者需要更多乘法和加法运算的Piecewise三阶多项式逼近，Piecewise二阶多项式逼近更具优势。因此，本文在每个分段子区间内使用二阶多项式进行运算，以逼近该子区间内的目标函数。

假设f(x)=arctan(x)/(2π),x∈[a,b)。[a,b)被划分为n个连续的子区间[ai,ai+1)，其中i=0,1,2,…,n-1。在每个子区间内采用的二阶多项式的统一形式如式(2)所示：

R=C0+D×(C1+D×C2)

(2)

其中,C0,C1和C2为多项式的系数，D是多项式的变量，R是多项式的运算结果。式(2)所示的二阶多项式形式相较于典型的二阶多项式形式减少了一个乘法运算。

假设xi是处于子区间[ai,ai+1)内的一个给定值，对函数f(x)进行二阶泰勒级数展开，可以获得式(2)中的系数和变量，如式(3)所示：

(3)

2.2 架构

图1展示了反正切运算器的硬件架构。图1中压缩单元根据反正切函数图像的中心对称性将输入映射到[0,1]。地址单元可根据信号x的阶码以及尾数的高m位获取xi,并通过译码获得地址信号Addr。查找表单元可根据信号Addr分别读取3个系数。减法单元完成D=x-xi的操作。之后2次乘加运算完成如式(2)所示的多项式运算。最后，规格化单元进行就近舍入和规格化操作，以输出符合IEEE-754标准的单精度浮点形式的结果。

Figure 1 Architecture of the arctangent operator图1 反正切运算器的硬件架构

3 二级分层分段

3.1 逼近误差分析

为了使反正切运算器的输出结果与标准结果之间的误差不超过1 ulp，又因为本文设计对输出结果使用就近舍入法最大可引入0.5 ulp的舍入误差，因此逼近误差必须小于0.5 ulp。根据泰勒定理，可以得到二阶多项式逼近的误差余项ε2，如式(4)所示：

(4)

其中，ξ是处于数轴上x到xi之间的一个数。

因此，逼近误差εa可以由式(5)给出：

(5)

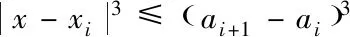
(6)

为了方便译码并减少子区间数量，本文使用二级分层分段方法，即在[2j,2j+1)内，其中j为负整数，进行均匀子区间划分，并使xi=(ai+1-ai)/2，且子区间大小随j的减小而逐步减小，以满足精度要求。根据式(6)获取每一个[2j,2j+1)内满足εa<0.5 ulp要求的子区间的长度，由此可得如表1所示的子区间划分。

特别地，对于子区间[0,2-12)内设置xi=0，此时根据式(2)和式(3)可得R=x×(1/(2π))；对于子区间[2-12,2-11)，本文设置xi=2-12。此外，对于x=1，设置C2=C1=0,C0=0.125，此时输出为0.125。

若使用均匀分段的方法，要达到相同精度，所需要的分段子区间的个数为1/2-12=212。表2展示了使用本文所述的二级分层分段进行非均匀分段和使用均匀分段方法所分别产生的子区间个数。

3.2 单调性分析

图2展示了使用如表1所示的二级分层分段子区间的Piecewise二阶逼近算法在2个相邻子区间[ai,ai+1)和[ai+1,ai+2)的交界处的单调性违例，且单调性违例区域大小为α=α1+α2。在ai+1的某个邻域内，任意相邻2个单精度浮点形式的数的距离为β=ULP(ai+1)，其中ai+1为单精度浮点形式。由图2可知，当β≥α时，单调性违例区域将不会对输出的单调性产生影响。

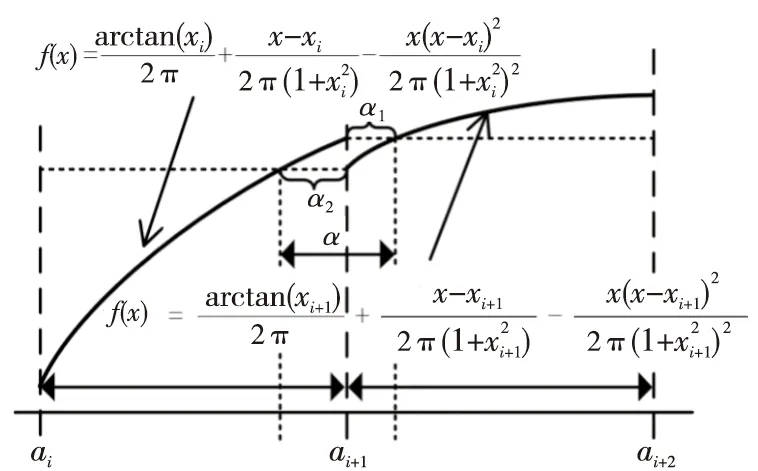
Figure 2 Monotonic violation at the junction of adjacent subintervals图2 2个子区间交界处的单调性违例

为了获得α2，假设：

(7)

如图2所示，当f(x1)=f(x2)时，根据式(2)和式(3)并忽略α2的高次项可得式(8)：

(8)

其中

(9)

(10)

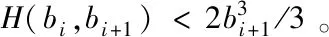
(11)

4 位宽设计与优化

4.1 静态分析

除舍入误差和逼近误差外，设计还需要考虑由于信号位宽有限而引入的量化误差。根据表1以及式(5)和式(6)可以得到逼近误差εa≤2-4ulp；又由于可允许的最大误差不能超过1 ulp，输出的最大舍入误差为0.5 ulp,因此必须使得量化误差εq≤(2-2+2-3+2-4) ulp。在如图1展示的架构中，量化误差来自于信号C0,C1,C2以及M0,M1,M2，假设其值分别为εC0,εC1,εC2以及εM0,εM1,εM2。根据图1、表1、式(2)和式(3)，可以得到式(12)：

(12)

根据式(3)可以得到22C2≥f(x)，又由于f(x)≤x/(2π)，则22ULP(C2)≥ULP(f(x))，其中f(x)为IEEE-754标准的单精度浮点数；更进一步地，根据式(2)可以得到εC2≤22ULP(C2)×D2；又根据表1可知,本文所述分段方式下D≤2-8-1，因此εC2≤ULP(C2)×2-16。

在位宽设计过程中，为了减少硬件成本且避免不必要的精度损失，本文分配了较大的量化误差给远离输出端的信号，如图1中所示的信号C2和M2；同时，分配较小的量化误差给远离输入端的信号，如信号C0和M0；此外，分配更大的量化误差给乘法运算输入，而分配更小的量化误差给加法运算输入。根据以上量化误差分配原则，本文分配的量化误差如式(13)所示：

(13)

由此，根据式(12)可以得到如表3所示的信号位宽。根据式(12)可知εC2≤ULP(C2)×2-16，又由于εC2=2-3ulp，则ULP(C2)≥2-13。因此，信号C2的尾数位数为24-13=11 bit，其中算式中的24是指IEEE-754标准的单精度浮点形式的输出具备24位尾数。因此，信号C2的位宽为1+8+11=20 bit，其中包含1 bit符号位，8 bit阶码位。

4.2 动态分析

为了优化信号位宽以压缩硬件成本，本文对[2-12,1]内的所有单精度浮点形式的输入以及对应的输出进行动态分析，其主要步骤如下所示：

步骤1减少指定信号位宽。

步骤2测试输出结果与黄金模型运算结果之间的误差是否不大于1 ulp，以及输出是否随输入的增加而逐步递增。如果测试通过则位宽减少成功；否则将信号位宽恢复到步骤1之前的状态。

步骤3重复步骤1和步骤2，直到完成所有指定信号的位宽优化。

5 仿真结果

由于反正切函数图像具备中心对称性，且在[0,2-12)内Output=Input×(1/(2π))。因此，对于[2-12,1]内的所有输入(Input)进行的测试被认为具备覆盖性，测试结果如图3所示。误差Error=|Output-Std|/ULP(Std)，其中Std为C语言数学库中对应函数的运算结果。由图3可知，反正切运算器的输出与黄金模型运算结果之间的误差不超过1 ulp，达到了设计精度要求。

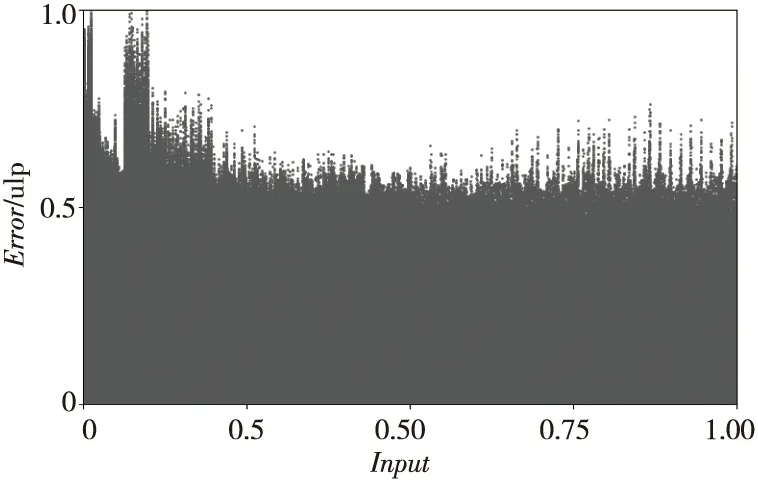
Figure 3 Error of the output of all inputs within [2-12,1]图3 [2-12,1]内所有输入的输出结果的误差

类似地，本文对[2-13,1]内的所有输入进行单调性验证。验证方法是将2个相邻输入(Input)的输出结果(Output)相减得到差(Differences)，其中对应于较大输入的输出作为被减数，获得的结果如图4所示。根据图4可知，所有的差都不小于0，即输出结果随着输入的增大而逐步增大，具备与原函数一致的单调性，达到了设计要求。

Figure 4 Monotonicity test results of the output corresponding to all inputs within [2-13,1]图4 [2-13,1]内所有输入对应的输出的单调性测试结果

进一步地，本文展示了所设计的反正切运算器与芯片TMS320F2837xD的指令ATANPUF32在输入处于(0.031017+0.3×10-7,0.031017+1.6×10-7)内的输出随输入变化的图像，分别如图5和图6所示。从图5可以知道，TMS320F2837xD的指令ATANPUF32的输出并不随输入的增加而逐步地递增，即存在单调性违例。从图6可知，在同样的输入范围内，本文所设计的反正切运算器的输出随输入的增加而逐步递增，且输出随输入变化的曲线相对于图5更加平滑。

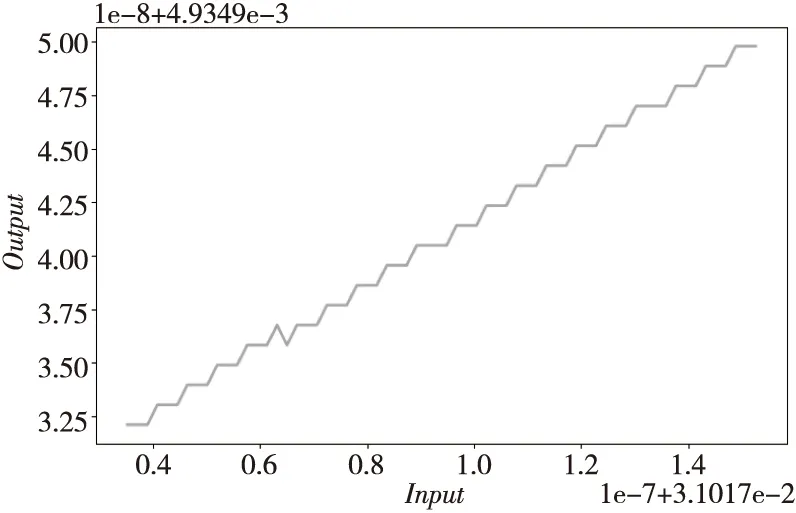
Figure 5 Output of the instruction ATANPUF32 in the TMS320F2837xD changing with the input图5 TMS320F2837xD的指令ATANPUF32的输出随输入变化的图像

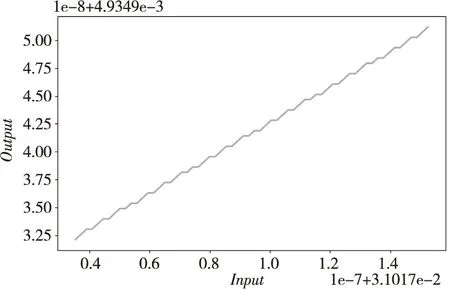
Figure 6 Output of the designed arctangent unit changing with the input图6 本文设计的反正切运算器的输出随输入变化的图像

为了比较硬件成本，本文使用XILINX Virtex-4 XC4VLX100-12 FPGA进行了硬件仿真。此外，为了获得无偏见的比较结果，该硬件仿真仅仅基于可编程的逻辑单元。本文还与文献[15]的设计进行了比较，其使用了与本文类似的Piecewise二阶逼近算法和二次乘加运算结构来完成类似的非线性函数运算。如表5所示，本文设计的反正切运算器在面积和延时2个方面都优于文献[15]的类似设计。

6 结束语

本文基于Piecewise算法设计了一个输入输出都符合IEEE-754单精度浮点标准的反正切运算器。逼近误差分析与二级分层分段方法相结合完成了运算区域的非均匀分段，达到了压缩系数表的目的。通过分析单调性违例区域的尺寸与对应子区间大小之间的关系，使得单调性违例区域的尺寸可控，从算法上确保了运算结果的单调性。此外，通过分析量化误差完成了关键路径上信号位宽的设计，并进一步通过有限范围内动态误差分析完成了位宽优化，达到了减少硬件成本的目的。仿真验证结果表明，本文设计的反正切运算器的硬件开销相较于同类设计更小，输出结果与黄金模型运算结果之间的误差小于1 ulp，且具备与原函数一致的单调性。