考虑荷载P-Δ 效应的陡坡段桥梁基桩变形计算
2022-08-19杨明辉李俊儒付大喜
杨明辉,李俊儒,付大喜
(1.湖南大学土木工程学院,湖南长沙 410082;2.北京交通大学土木建筑工程学院,北京 100044)
随着西部山区基础设施(如高速公路、高速铁路等)的大力修建,出现了越来越多的位于陡坡上的桥梁桩基础.由于特殊的地形特点,相比平地基桩,陡坡基桩具有以下三个突出特点[1-7]:1)横向承载能力弱,边坡一侧土体的缺失造成土体的抗力显著降低,且浅层尤为明显;2)具有较长的自由段,桩顶与边坡垂直距离大而形成较长自由段;3)承载复杂,承受竖向自重荷载、横向边坡荷载等荷载的耦合作用.因而陡坡基桩的P-Δ效应将更为显著,从而造成安全隐患.可见,合理考虑P-Δ放大效应成为陡坡段基桩设计计算的关键问题.
P-Δ效应即结构的侧向位移与竖向荷载引起的二阶效应,属于经典的结构力学问题[1].对于基桩结构P-Δ效应,考量的关键则在于土体作用力的合理模拟.近年来,已有大量国内外学者对该问题进行了研究.一方面,如Sastry 和Meyerhof 等[8-10]对倾斜荷载下基桩承载力性能进行了大量的室内模型试验研究,从而给出单桩承载力的半经验公式,该公式中包含了P-Δ效应的影响;赵明华等[11-12]分别采用m法和C 法考虑P-Δ效应,推导得到了倾斜荷载作用下单层均质土中基桩内力及位移的幂级数解;邢康宇等[13]通过引入双曲线型水平荷载传递模型考虑桩-土体系的非线性变形情况,导得可考虑P-Δ效应与横向荷载共同作用下高桩基础水平响应的非线性有限差分解;栾鲁宝等[14]给出了黏弹性土中考虑P-Δ效应时基桩水平振动的解析解答;Zhang 等[15]、Zhu等[16]和Zhang 等[17]分别采用水平弹簧和竖向弹簧来模拟桩-土相互作用,导得了轴、横向荷载同时作用时单桩响应的半解析解等.另一方面,不少学者直接采用半数值方法建立刚度矩阵来考虑该问题.如邹新军等[18]基于地基加权刚度的概念考虑地基土成层、非均匀性及大变形,建立了倾斜荷载下基桩的有限元-有限层模型;赵明华、李微哲等[19-20]则计入土体剪切变形,建立了可考虑二阶效应的杆单元刚度方程,并基于MATLAB程序给出了解答.
上述方法均仅针对平地上的基桩,关于陡坡基桩的P-Δ效应问题,目前研究较少.仅有尹平保等[21-22]基于弹性地基梁的假设,给出了陡坡桩桩基承载力的幂级数解答,赵明华等[23]在类似假定条件下给出了相应的有限差分解答,但二者均假定土体为支撑弹簧,从而无法考虑土体连续性以及桩土之间复杂的三维相互作用,而数值方法虽可避开该问题,但显然求解过程过于复杂,不便于实际工程应用.鉴于此,本文基于变分原理,考虑桩周土体连续性、桩土整体系统能量转换及P-Δ效应导得陡坡段基桩复杂荷载作用下桩身响应的半解析解,并开展室内小模型试验进行验证与对比分析;最后,对影响陡坡段基桩P-Δ效应的主要因素进行了探讨,供工程设计参考.
1 计算模型
1.1 计算模型分析
如前所述,由于基桩地理位置特点及荷载的复杂性,基桩水平变形极易引起竖向力附加效应(P-Δ效应).因此,建立基桩-土体一体化模型,重点分析桩土变形对二阶效应的影响,如图1 所示.基桩总长为Lp,截面半径为rp,桩身抗弯刚度为EpIp,基桩的自由段长度以L0表示,并在桩顶分别承受水平向荷载P0、竖向荷载N0以及外部弯矩M0,陡坡的坡角为β.为分析桩周岩土体的非均值性,假定土体分为n层.为方便分析,以桩基自由段桩顶中心为极点建立极坐标系.
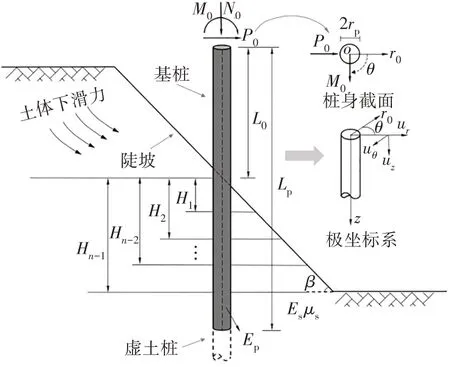
图1 陡坡段基桩受力模式Fig.1 Force model of single pile in steep slope section
1.2 土体位移模式
在桩-土一体化系统中,计算土体位移的关键在于确定土体的变形模式.考虑到实际工程中安全性要求,仍假定桩土始终变形协调,受荷过程中桩土界面接触紧密.桩土位移场域描述为:受到桩身位移影响的土体位移场是以桩身轴线为圆心的圆柱体位移场,在远离桩基础一定距离后,土体位移递减至零[24-30].Sun[28]和Basu等[29]认为与侧向荷载相关的垂直位移uz可以忽略不计,土体的径向和切向水平位移可以由柱坐标r、θ、z表示.为简化计算,本文沿用该模式,且认定边坡始终稳定,则在桩身影响范围内,土体的位移可以近似写成:

式中:ur和uθ分别为土体单元在径向及切向的位移分量;ϕr(r)和ϕθ(r)是土体位移衰减函数.土体单元到桩身的距离用r表示,显然,当r增大至临空面时,土体衰减函数为零.
由土体位移的方程即可导得土体应变和桩身挠曲位移的关系,见式(2).
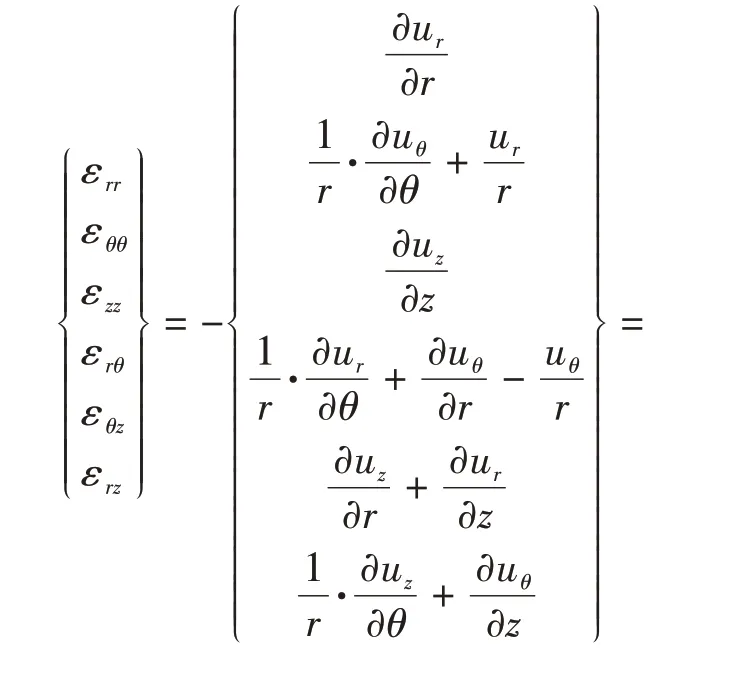
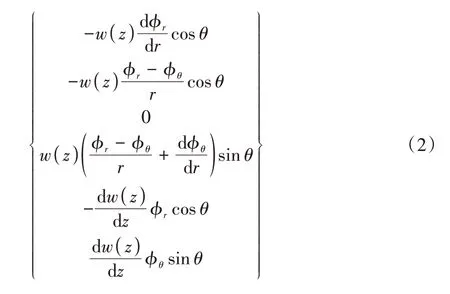
2 陡坡段桩土体系能量方程建立
2.1 系统总能量方程建立
陡坡桩-土体系总势能方程由桩身屈曲应变能Πpile、陡坡土体应变能Πsoil以及外部荷载做功Πload组成:

方程(3)中前三项分别为桩身弹性形变能、成层桩周土体应变能以及桩底虚土桩土体应变能,后三项则为作用在桩顶的水平荷载做功、外加弯矩做功以及桩身竖向轴力做功.εpq、σpq分别为应力和应变张量.将土体应力张量方程(2)代入总势能方程(3),根据最小势能原理取总势能变分为零,则方程(3)可改写为:
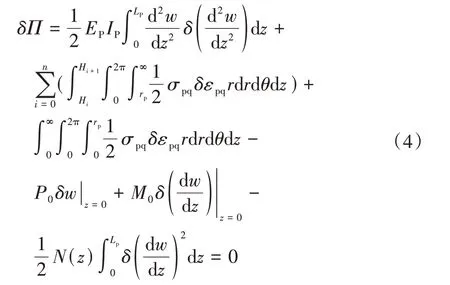
合并所有含有挠度w及其导数的项,利用分部积分法将其中高阶变分项改写成只含有δw和其一阶导数的方程,可以得到:

再合并总势能方程得变分形式(4)中所有含有φθ、φr以及二者相关导数项:


2.2 求解微分控制方程
根据最小势能原理,当系统在外力作用下处于稳定平衡状态时,将存在一组满足边界条件的位移使系统的总势能最小,即存在一组满足边界条件的位移使系统总势能的变分等于零,使方程(5)中有关桩身水平位移变分项为零,将δw前系数均取为0,从而得到不同区域桩身控制微分方程及其对应的边界条件.
当0<z<L0时,控制方程如式(9):
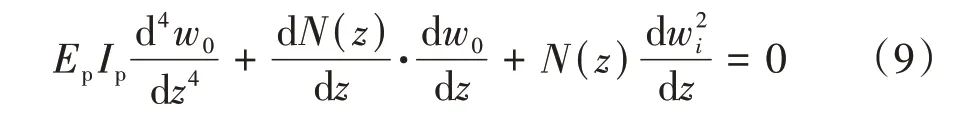
当0<z<Lp时控制方程如式(10)(下标表示对应的土体分层)所示:
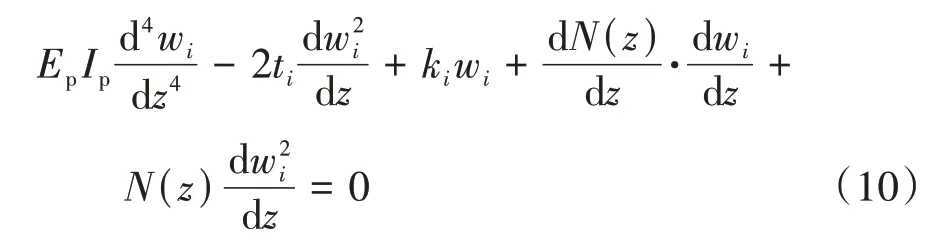
边界条件:当z=0时(即顶部自由),
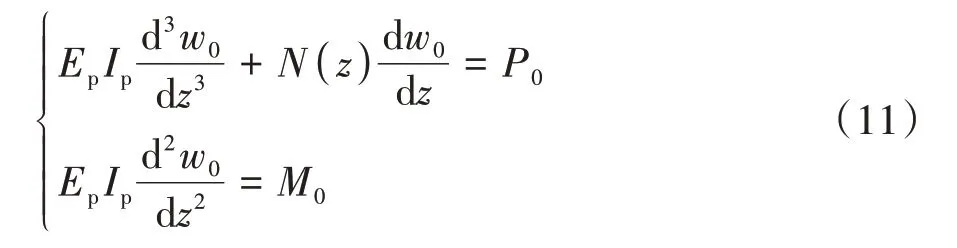
当z=L0(基桩与陡坡交接处)时,
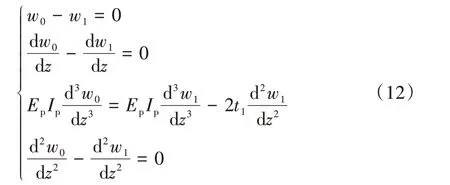
当z=Hi(土层交接处)时,
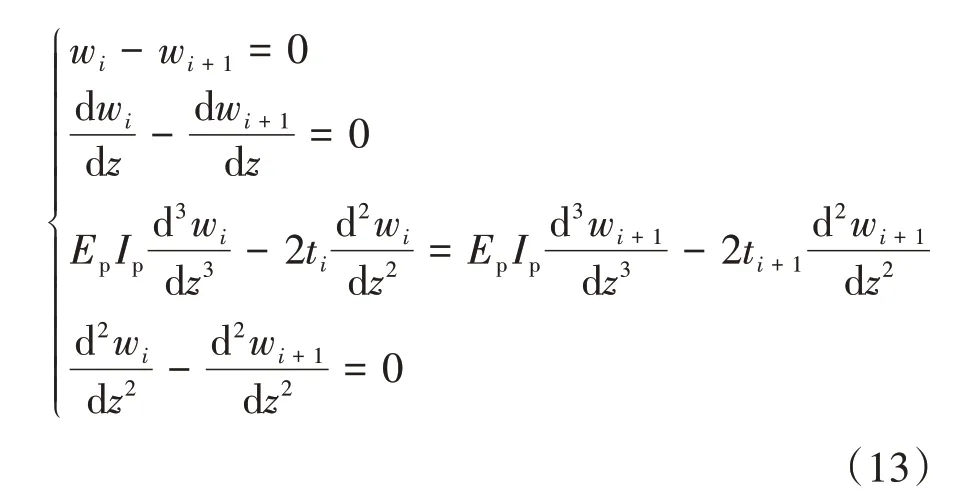
当z=Lp时,则有:

同样通过将方程(7)中与衰减函数相关项的变分取为0 的方式得到关于土体径向和切向衰减函数的控制微分方程以及其边界条件:
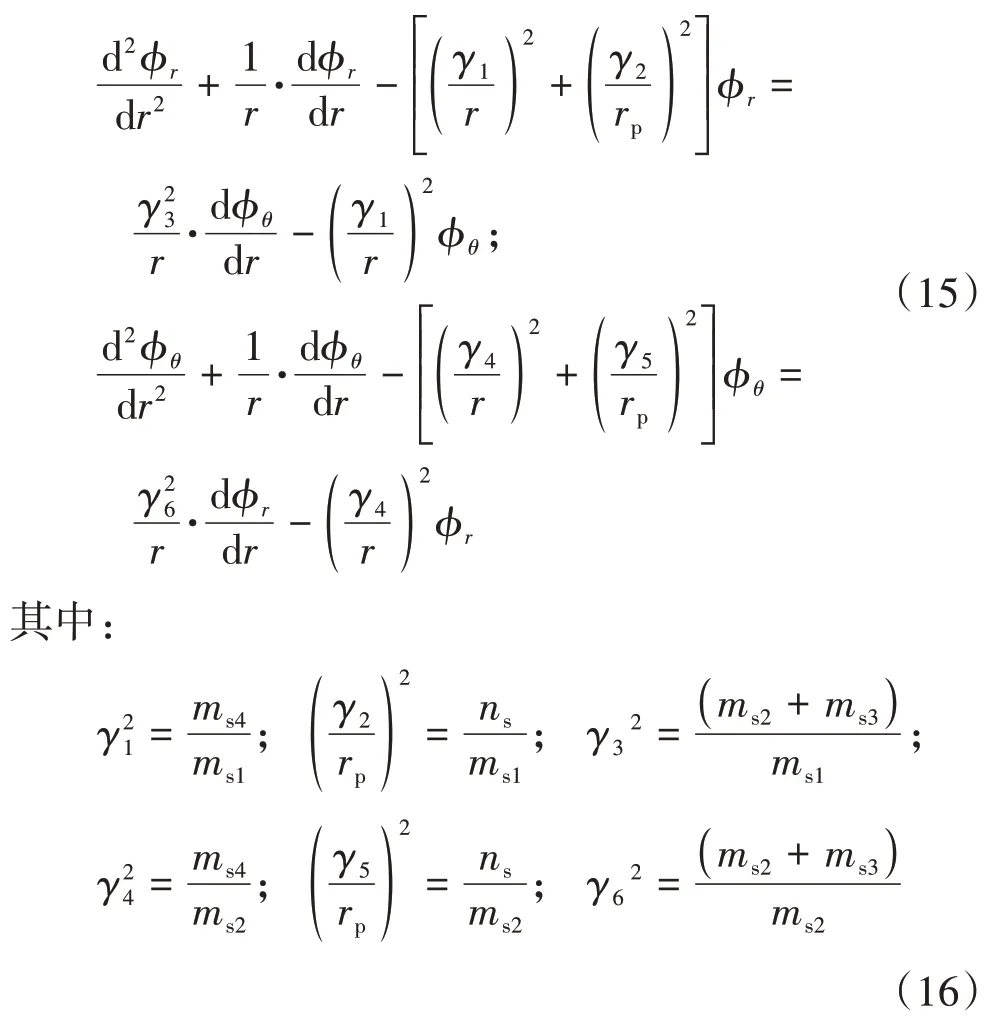
土体径向和切向位移在桩身处与桩身位移相等,衰减函数取值为1,随着与桩身距离增大,位移逐渐减小至0.由于陡坡斜角β的存在,衰减函数的边界条件会随着不同土层变化,临空面以外的土体位移全部视为0,由此可得土体衰减函数的边界条件如式(17):
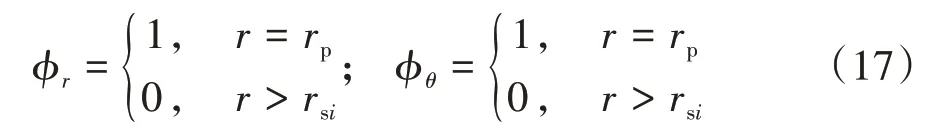
其中rsi为当前所在土层Hi中某深度z处对应的基桩节点到陡坡临空面的距离.由基桩和陡坡面的几何关系可知rsi=(z-L0)/tanβ.
2.3 迭代求解
桩身控制方程和土体衰减函数的控制方程不是通常的高阶微分方程,两个方程存在一定程度的耦合,利用一般方法无法得到准确解析解.因此,采用差分方法写出差分形式的方程,同时利用软件MATLAB 编写计算程序进行迭代计算得到控制方程的半解析解.
如图2 所示,将桩周土体分为n段,土层以上自由段长为L0,同时将自由段分为k0个节点,每段长度为h0,在桩顶以上和地面以下分别取虚拟节点-2、-1、k0+1、k0+2.将地面以下每个土层中的桩体划分为ki段,每段长度为hi,在每层土层的上下交界处也设置4个虚拟节点-2、-1、ki+1、ki+2.基于上述的节点网格划分,将式(9)和式(10)写成如式(18)和式(19)所示差分形式.
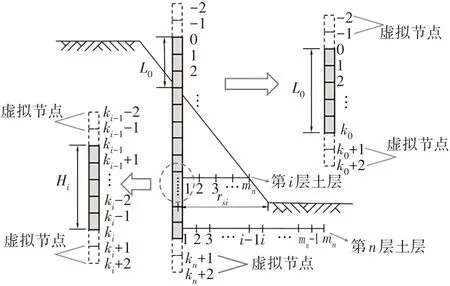
图2 基桩离散过程Fig.2 Discrete process of foundation pile
当0<z<L0时,

当L0<z<Lp时,
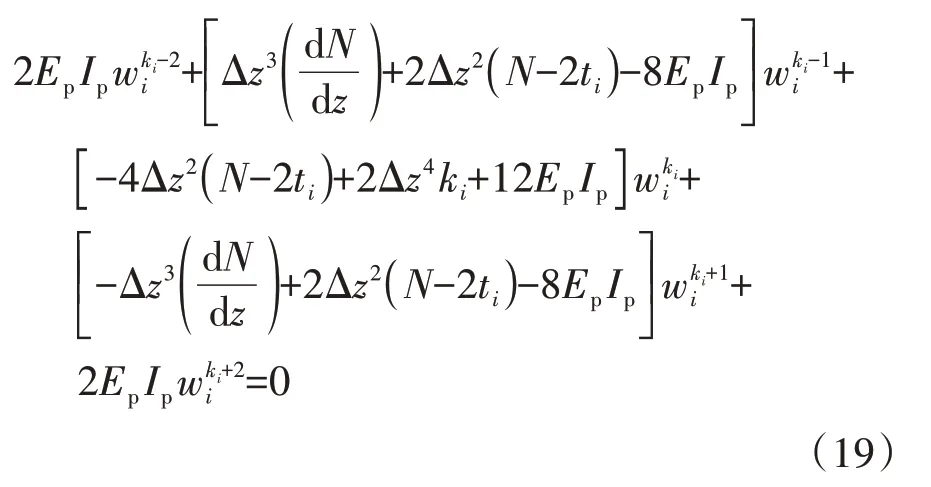
桩身控制微分方程在各个节点处的边界条件[式(11)~式(14)],同样写成差分方程的形式.桩顶以及桩端的边界条件差分形式为:
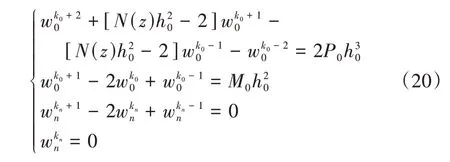
土层交界处考虑虚拟节点的边界条件为:
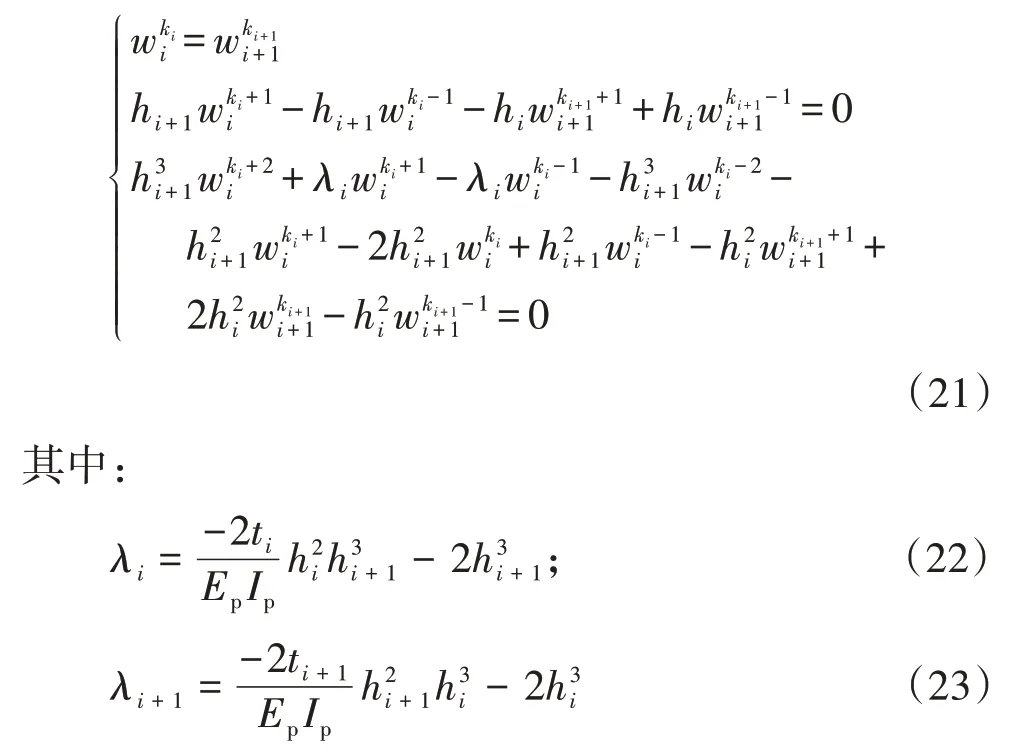
通过边界条件将虚拟节点用内部节点的位移表示,进而可得关于桩身水平位移的变系数齐次方程组,即组成Kw=F的形式,其中w为各节点位移组成的位移向量,K为系数矩阵,其阶数与网格划分数量相同.同样,土体水平位移衰减函数φr(r)和φθ(r)的控制微分方程亦可写成相同差分形式进行求解.
桩身位移解与土体衰减函数的解两者相互关联,式(6)与式(16)分别由衰减函数和挠度函数决定,因此需要采取迭代算法求解耦合微分方程.在第一次迭代计算中,将出现在挠度方程组中的系数γ1至γ6初步假设为1,通过上述解法求解出一个中间解,再由中间解计算得到衰减函数的计算系数,并将得到的衰减函数的中间解重新代入挠度方程组,进入第二次迭代.迭代得到挠度方程的解,误差小于10-6,迭代停止.求解迭代过程如图3所示.
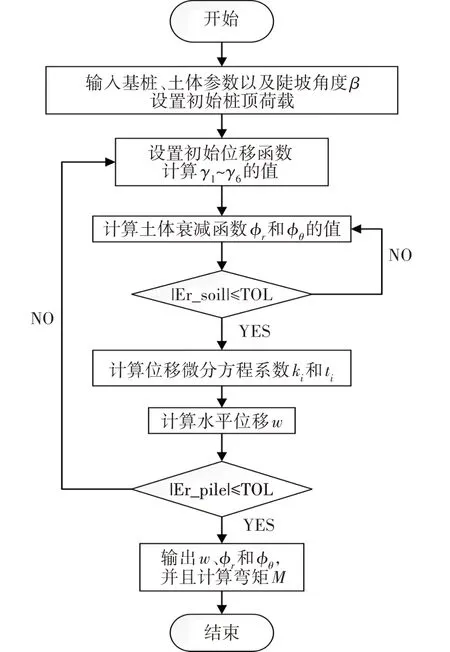
图3 迭代求解流程图Fig.3 Flow chart of iterative solution
3 试验验证
为验证前述方法的合理性,设计完成了一组室内陡坡单桩模型加载试验.模型桩采用直径为25 mm、壁厚为2.5 mm的铝管,桩长100 cm,抗弯刚度EI=145.11 N·m2,试验中分别设置不同的自由段进行对比分析.桩周岩土体选用了两种不同配合比的石膏、水泥、砂的混合料进行模拟以反映桩周岩土体的非均质性.混合料用量如表1所示.

表1 混合料用量表Tab.1 Table of mixture consumption
试验过程中,保持坡上堆载以及桩顶水平荷载不变,桩头竖向荷载N0分级施加(图4),以容许最大位移作为终止加载标准,即桩身地面水平位移或竖向位移达到0.15 倍桩径时认为局部岩土体塑性破坏,停止加载.通过在桩顶布设百分表2、3(量程30 mm)测定桩顶水平位移.每根桩前后两面均对称布置有应变片,每边各9片,共18片,其尺寸为3 mm×5 mm.由桩身布置的应力片测得桩身内力响应的变化.
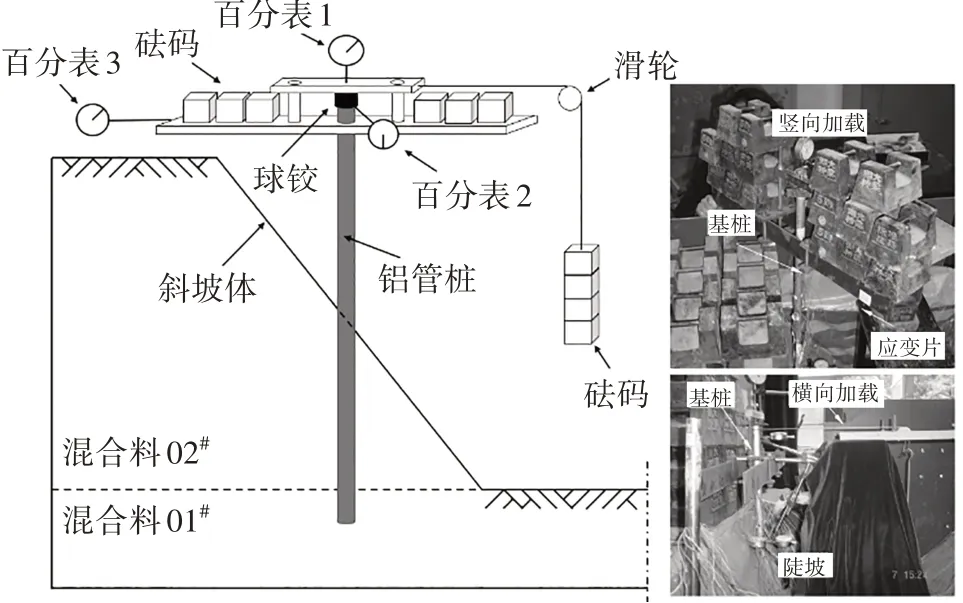
图4 模型桩加载装置Fig.4 Loading device of model pile
图5为不同自由段长度时各级荷载下桩顶水平向位移的计算值与测试值的对比.由图5可知,理论计算曲线与实测点的趋势完全一致,最大误差仅为6.7%.
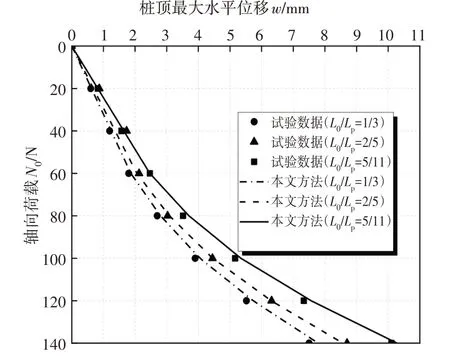
图5 桩顶位移试验与理论对比Fig.5 Comparison between experimental and theoretical values of pile top displacement
图6 所示为不同自由段长度时各级荷载下桩身弯矩计算值与测试值的对比情况.由图6可知,理论计算值与测试值吻合较好,而不同自由段长度的陡坡段桥梁基桩内力分布规律基本一致,即桩身弯矩在地面基桩以下较小范围内即达到最大值,之后,随着埋深增加急剧减小,在到达零点之后,出现反向弯矩,最后衰减至零.若不考虑基桩的P-Δ效应,则无法考虑竖向荷载与水平荷载的耦合效应.
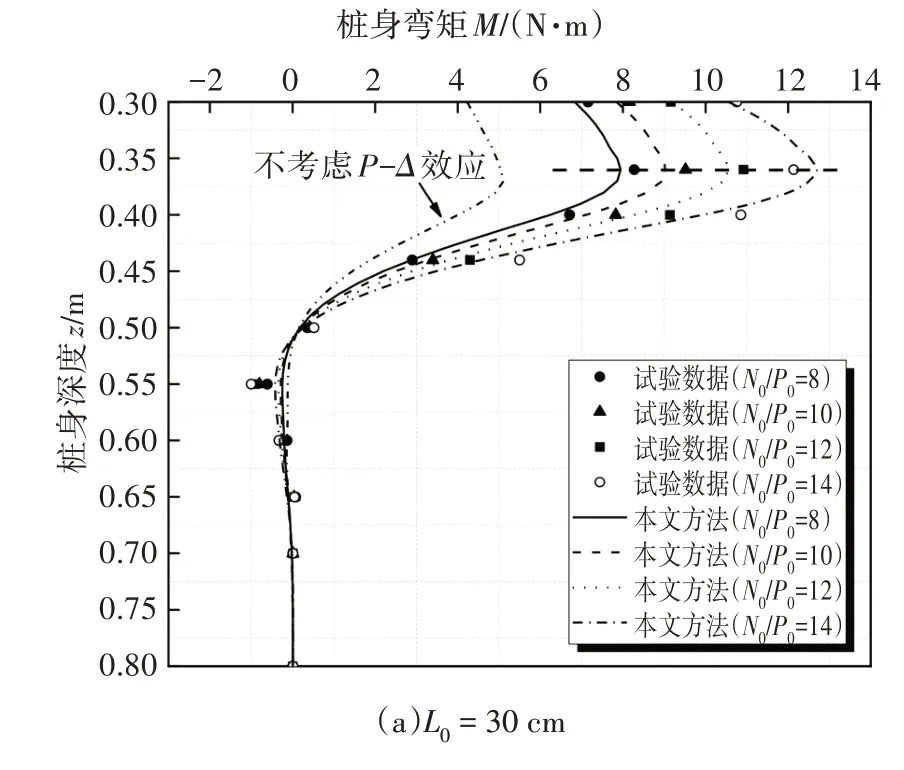
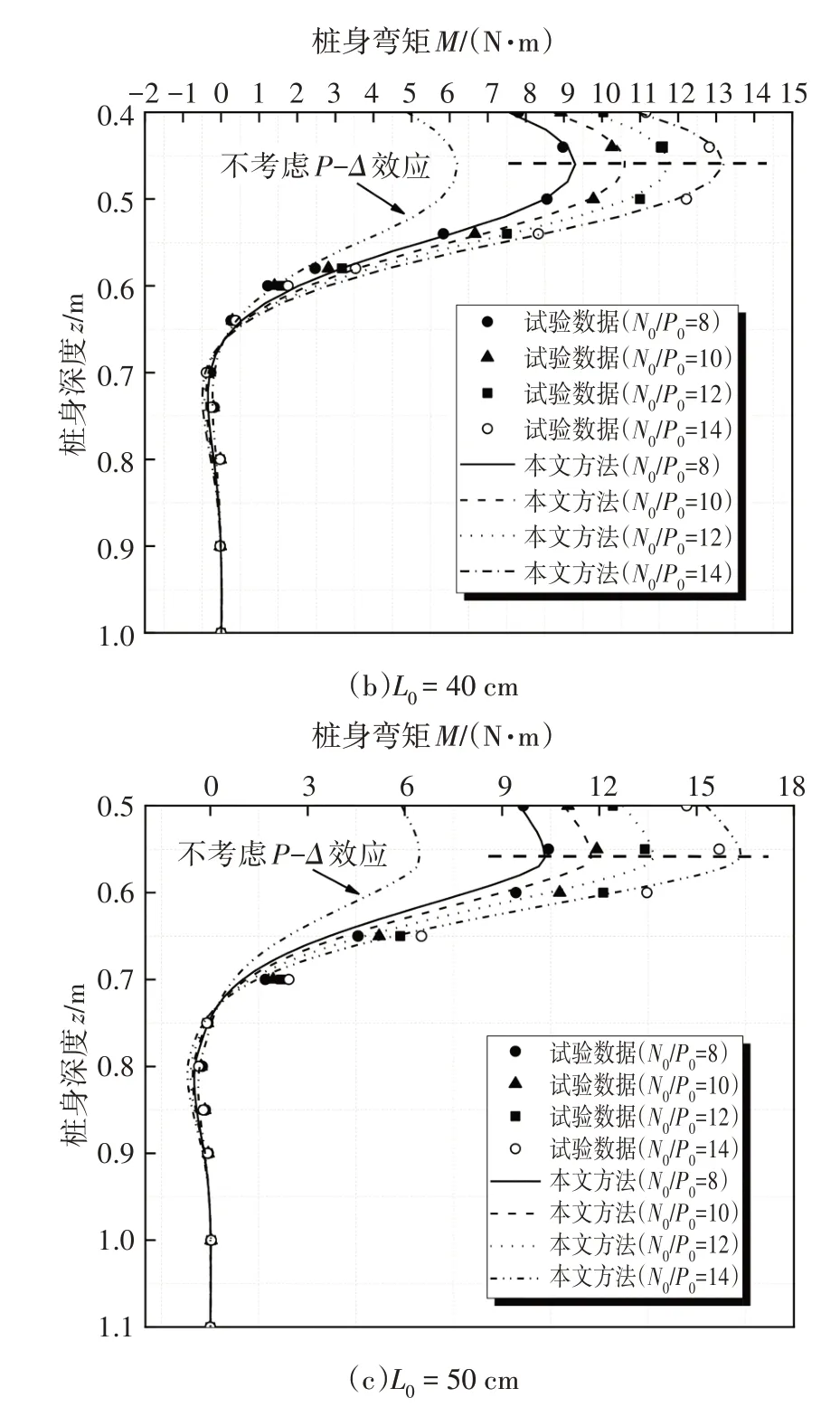
图6 桩身弯矩试验对比Fig.6 Comparison between test value and theoretical value of maximum bending moment of pile
4 参数分析
以下对陡坡段基桩P-Δ放大效应的主要因素进行分析.基本参数取值如下:总桩长Lp=30 m,自由段长度L0=10 m,桩径d=1.8 m,桩身弹性模量Ep=18 GPa;土体分两层,其弹性模量分别取Es1=10 MPa,Es2=20 MPa;桩顶水平向荷载P0=200 kN,外部弯矩M0=200 kN·m.
4.1 竖向荷载与水平荷载比值影响分析
根据结构力学原理,P-Δ放大效应的发挥与竖向荷载和水平荷载的比值直接相关,该比值是控制杆体单元稳定性的重要指标.图7、图8 分别为水平向荷载与竖向荷载不同取值情况下的陡坡段基桩的位移及内力响应,为考虑坡度的影响,选择了3 个不同边坡角度进行分析.
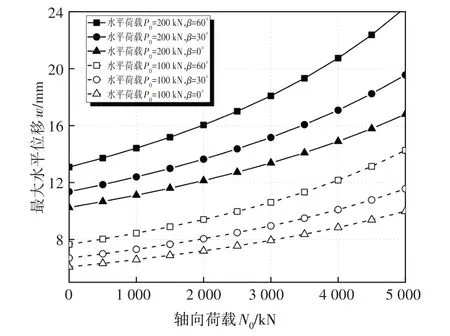
图7 不同轴横向荷载比下的桩身最大水平位移变化规律Fig.7 Maximum displacement of pile shaft with different axial transverse load ratio
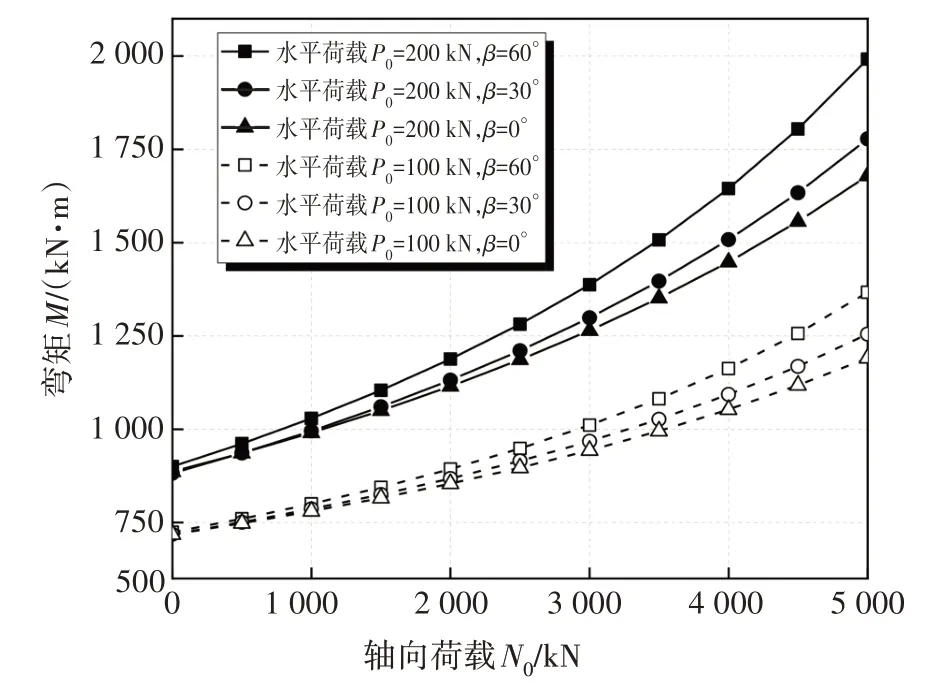
图8 不同轴横向荷载比下的桩身最大弯矩变化规律Fig.8 Maximum bending moment of pile shaft with different axial transverse load ratio
由图可知,竖向荷载的增大将明显地增大基桩的水平变形与内力值.且其增长幅度随竖向荷载的增大而增大,边坡角度的影响同样明显.以水平荷载P0为200 kN 为例,竖向荷载取10 倍水平荷载,当陡坡坡角β为30°时,桩顶最大位移由12.14 mm 增加至13.64 mm,而桩身最大弯矩则由1 114.81 kN·m 增加到1 131.58 kN·m;当坡角增大至60°时,桩顶最大位移增大至16.05 mm,桩身最大弯矩增大到1 187.7 kN·m.由此可以看出随着坡度角的增大,桩基础的P-Δ放大效应对位移影响由12.36% 增大至17.67%,对弯矩影响由1.50%增大至4.96%,表明陡坡角度增大会加剧基桩变形的P-Δ效应.
4.2 自由段长度的影响分析
位于陡坡段的桥梁基桩,一般具有较大的自由段长度,而通过基桩自由段长度和其与总长度比值,以及基桩所在陡坡的坡角,可确定基桩与坡面的相对位置.同时,自由段长度与桩身水平位移以及桩身最大弯矩有着密切的关联[7].为研究自由段长度大小对陡坡基桩P-Δ效应的具体影响,在总长度相同的情况下,分析不同自由段长度基桩水平位移及其桩身弯矩的变化规律,见图9、图10.

图9 不同自由段长度时桩顶最大水平位移变化规律Fig.9 Variation law of pile top maximum displacement with different free length

图10 不同自由段长度时桩身最大弯矩变化规律Fig.10 Variation law of maximum bending moment with different free length
由图易知,在相同荷载条件下陡坡桩身水平位移和桩身弯矩随着自由段长度增大而增大,且自由段长度与总长度比大于1/5 时,桩身响应增长加快.但亦可看出边坡的影响,以自由段长度10 m为例,相比平地情形(β=0°),边坡角度β=30°时,考虑P-Δ效应与不考虑P-Δ效应的最大基桩水平位移差值由4.04 mm 增大到4.71 mm,桩身最大弯矩差值则由354.65 kN·m 增大到405.26 kN·m;而坡角增大到60°时,该差值则到达5.78 mm 和472.18 kN·m.位移增幅由16.58%增加至22.72%,最大弯矩增幅由14.26%增加至16.52%.由此可见,边坡坡度的增大加剧了基桩变形的P-Δ效应,因此在对位于边坡上的基桩进行受力分析时该效应不容忽视.
4.3 土体刚度影响分析
桩周土体的承载弱化效应是陡坡段基桩区别于平地情形的主要特征,为研究该因素对陡坡段基桩变形P-Δ效应的影响,取桩体和平均土层弹性模量比值Ep/Es分别为1 000、2 000、5 000.桩顶水平荷载取为P0=200 kN,弯矩为M0=200 kN·m,竖向荷载取值为N0=4 000 kN.
由图11、图12 可知,土体刚度的增强,可明显地减小基桩的水平位移与弯矩,表明土体约束的强化是减小P-Δ效应的重要原因.以Ep/Es=5 000 为例,对比平层桩和陡坡桩,陡坡基桩最大水平位移由4.67 mm增大至6.08 mm,桩身最大弯矩由23.40 MN·m增大至27.88 MN·m,分别增长30.19%和19.15%,同时最大弯矩出现位置会随着模量比的增大而下移,进一步表示陡坡坡角对P-Δ效应的促进作用.

图11 不同土体刚度对基桩位移的影响Fig.11 Influence of different soil stiffness on pile displacement
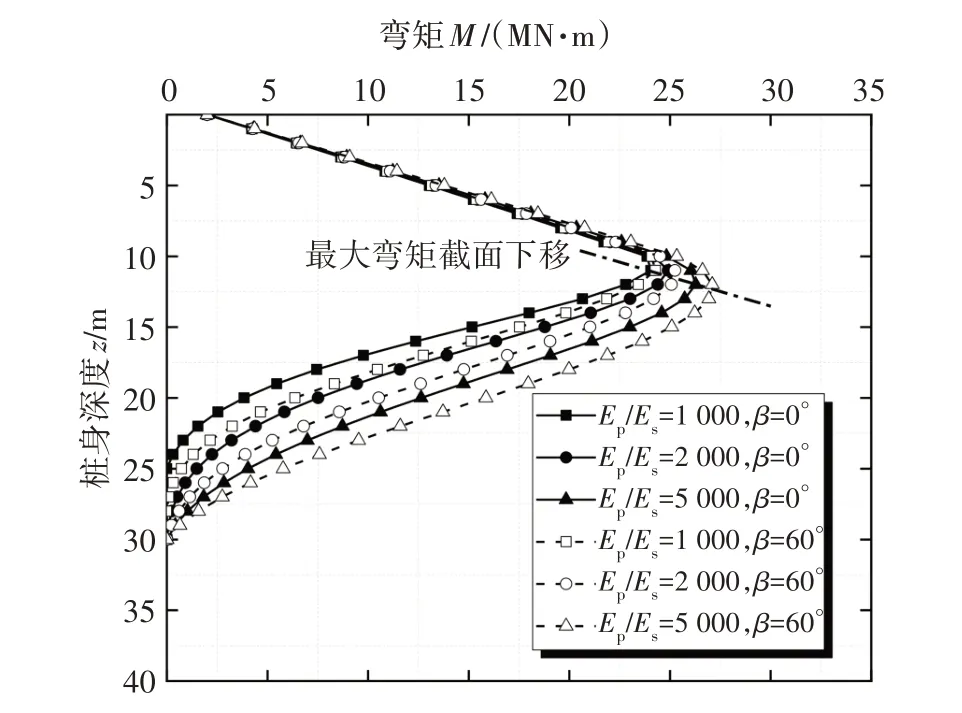
图12 不同土体刚度对基桩弯矩的影响Fig.12 Influence of different soil stiffness on pile bending moment
5 结论
本文引入能量变分原理,对陡坡段基桩变形的P-Δ效应进行了模拟,从而为该问题的解决提供一种新思路,而后开展了相应的室内模型试验进行验证,并对其影响因素进行了分析,结论如下:
1)基于最小势能原理,建立了陡坡段基桩-边坡土体系统的总能量控制微分方程.结合不同边界条件及桩土位移条件,得到了可考虑P-Δ放大效应的陡坡段基桩变形的半解析解答.
2)开展了陡坡段基桩承受复杂荷载的室内加载试验.对比分析表明,本文理论方法所得基桩变形内力与实测值吻合良好,可较好地模拟复杂荷载下陡坡段基桩变形的P-Δ放大效应.
3)对影响陡坡段基桩P-Δ放大效应的主要因素进行了对比分析.计算结果表明,陡坡段桥梁基桩的P-Δ放大效应与轴横向荷载比以及桩顶自由段长度正相关,随着土体刚度的增强而有所减小.量化分析表明,陡坡坡度角增大对桩体P-Δ效应有明显的加剧作用,坡角的影响不容忽视.
