成层土中竖向受荷桩沉降性状简化计算方法

王立兴，吴文兵†，梅国雄，，闻敏杰，3，徐美娟

（1.中国地质大学（武汉）工程学院，湖北武汉 430074；2.广西大学土木建筑工程学院，广西南宁 530004；3.浙江理工大学建筑工程学院，浙江杭州 310018）

桩基础由于承载力高、稳定性好、适应性强等特点，已经被广泛应用于高层建筑、桥梁公路等构筑物的基础建设中.在桩基设计中，竖向受荷桩的承载机理和沉降特性分析是至关重要的.目前，基桩沉降计算方法有荷载传递法［1-2］、弹性理论法［3-4］、剪切位移法［5-6］和数值计算法［7-8］等，其中荷载传递法是Seed和Reese［1］基于桩身荷载传递机理提出的，可以灵活地选取不同的荷载传递函数模拟桩与桩侧土非线性相互作用特性及地基土的层状特性，得到了广泛应用.荷载传递法的准确性主要依赖于荷载传递函数的合理性，荷载传递函数即剪应力与桩土相对位移之间的关系，传统的荷载传递函数主要有理想弹塑性模型［9-10］、双折线硬化模型［2，11］、三折线模型［12-13］、双曲线模型［14-15］及侧阻软化模型［11，16-17］.然而土与混凝土结构面的剪切试验［18-19］发现当剪应力小于某一个临界值时无相对位移产生，表明土与混凝土结构物之间应当存在初始临界摩阻力，赵明华等［20］和Zhang 等［21］分别提出了考虑初始临界摩阻力的改进双曲线模型和侧阻软化模型用于桩基沉降计算，通过实例分析验证了考虑初始临界摩阻力的非线性荷载传递模型可以更准确地模拟桩土相互作用特性，具有更好的工程适用性.

另外，传统的荷载传递法进行基桩沉降计算时简化地用折线硬化模型［11，21］或双曲线模型［17，20］来表征桩端荷载与位移的关系，这样无法考虑桩端土体的层状特性和桩端应力扩散效应.为此，王奎华等［9-10］、Wu 等［22］提出虚土桩模型来模拟桩端土对桩的支撑作用，并将虚土桩模型应用于层状地基中的单桩沉降计算分析和基桩动力特性研究［23-25］.进一步，王立兴等［26］将应力泡形虚土桩模型应用到单桩沉降分析来考虑桩端应力扩散效应的影响，但是文中采用双折线函数模拟桩侧阻力具有一定局限性，因此，有必要进一步对采用侧阻非线性荷载传递模型结合端阻应力泡形虚土桩模型的成层土中竖向受荷桩的沉降特性展开研究.

综上，本文采用应力泡形虚土桩模型和考虑桩土界面初始临界摩阻力的改进双曲线模型，分别模拟桩端土体对桩体的支撑作用和桩侧摩阻力与桩土相对位移间的关系，并在上述两种模型的基础上提出一种考虑桩土界面初始临界摩阻力影响和桩端应力扩散效应的成层土中竖向受荷桩的沉降特性简化迭代计算方法.通过工程实例对比验证了本文提出计算方法的合理性，并进一步分析研究了不同桩顶荷载作用下，竖向受荷桩的桩顶荷载沉降曲线、桩身压缩与桩端沉降所占比重变化情况、桩身轴力分布规律以及桩侧摩阻力发挥特性等单桩沉降性状.

1 计算模型及基本假设

1.1 桩侧荷载传递模型

为考虑桩土界面初始临界摩阻力和桩土非线性相互作用，本文采用赵明华等［20］提出的改进双曲线荷载传递模型来模拟桩侧摩阻力与桩土相对位移之间的关系，如图1 所示，该模型适用于正常固结黏土、中密砂与松砂等土体类型，其函数表达式为：

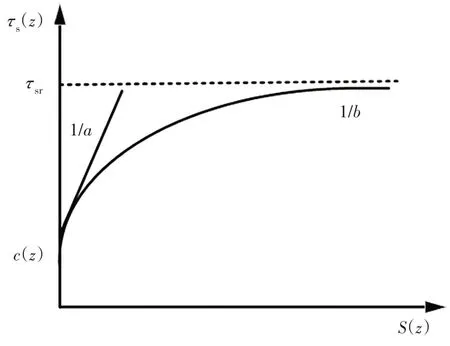
图1 改进双曲线荷载传递模型Fig.1 Improved hyperbolic load transfer model

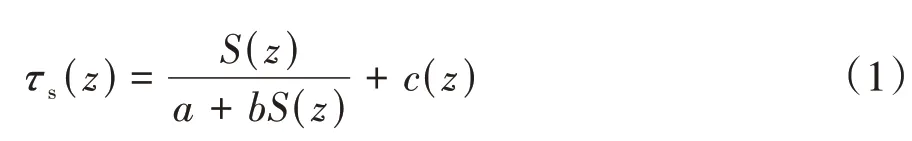
式中：τs(z)是深度z处的桩侧摩阻力；S（z）是深度z处的桩土相对位移；参数a、b为模型参数，其物理意义分别为曲线原点处的切线斜率的倒数和桩侧极限摩阻力τsr的倒数；c（z）为深度z处桩土界面初始临界静摩阻力.参数a、b和c（z）的值可通过现场载荷试验结果的反分析确定或通过室内土-结构接触面剪切试验获得.

1.2 桩端泡形虚土桩模型

辛公锋［27］通过对4 根现场试桩实测数据的反演，发现桩在极限承载力下桩底土体大部分仍处于弹性状态，因此，可以采用Boussinesq 解计算桩端附加应力范围，并利用弹性力学知识进行桩端土体沉降计算.假设桩端对土体的作用力为均布荷载形式，在桩端底面建立如图2 所示的极坐标系，将Boussinesq 解进行二重积分可以求得圆形均布荷载作用下桩端土体中任意一点的竖向应力分布为［25-26］：

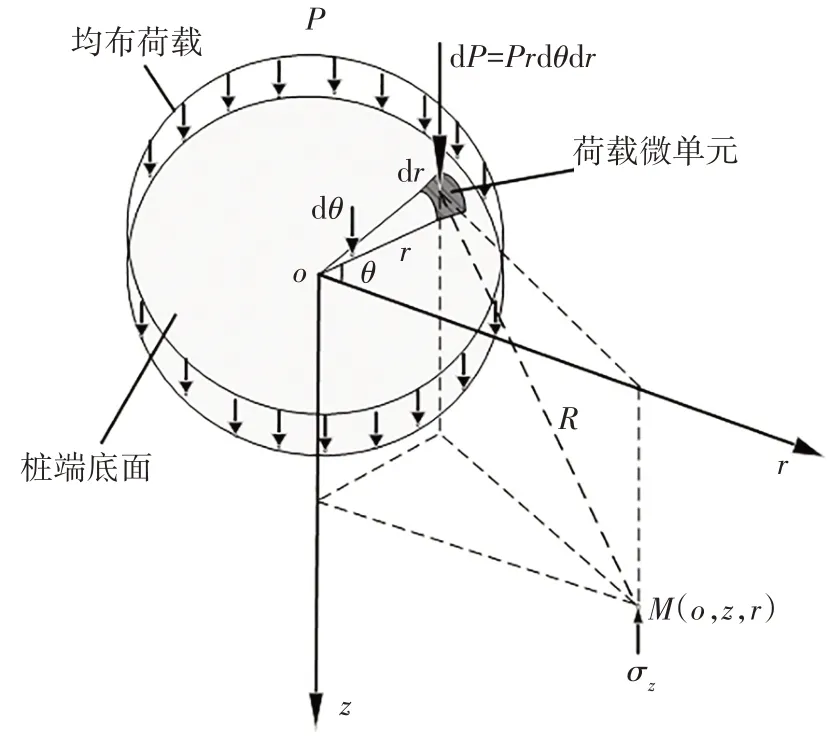
图2 桩端附加应力计算极坐标系Fig.2 The polar coordinate system of pile tip additional stress calculation

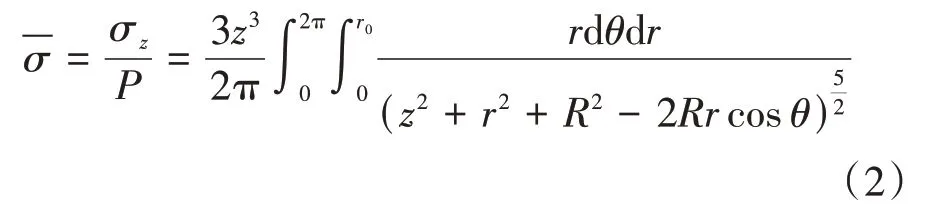
对式（2）进行数值求解可以得到一组竖向附加应力等值线，将等值线绕z轴旋转一周就形成三维附加应力等值面，假设应力等值面外的土体内附加应力很小，将等值面内的土体看作受荷主体进行计算，如图3所示.

1.3 桩土相互作用模型及相关假设

桩土相互作用体系简图如图3 所示，根据地基土层的成层性情况将实体桩和虚土桩一共分为n段，其中实体桩分成m段，虚土桩分成n-m段.从实体桩顶部向下依次编号为1，2，…，i，…，m，m+1，…，n；各桩段厚度分别为l1，l2，…，li，…，ln.实体桩总长为L1，虚土桩总长为L2，各段桩的埋深分别为z1，z2，…，zi，…，zn.桩顶作用的竖向荷载为P1，产生的桩顶位移为S1，荷载向下传递，假设第i段桩的桩顶轴力为Pi，相应的桩顶位移为Si，桩侧摩阻力为τsi.

图3 桩土相互作用模型Fig.3 The pile-soil interaction model

为简化计算，本文桩土体系相关假设有：

1）实体桩桩身截面均匀，虚土桩以应力泡的形式存在，其边界由式（2）求得；

2）虚土桩的力学行为与实体桩相符合，参数取土体实际参数；

3）虚土桩的变形仅考虑弹性状态，虚土桩底部为刚性支撑不发生变形；

4）实体桩与虚土桩的各桩段界面之间为完全连续接触，满足连续性条件；

5）地基中同一土层的物理力学性质沿深度方向不变.

2 单桩沉降计算流程

单桩的沉降由桩端土体的沉降和实心桩体的压缩两部分组成.本文采用应力泡形虚土桩模型来模拟桩底土体对实体桩的支撑作用，采用考虑初始临界摩阻力的双曲线荷载传递模型来模拟桩与桩周土体的相互作用，实体桩和虚土桩的压缩沉降量之和，即为所求实体桩的桩顶总沉降量.

首先推导虚土桩的沉降计算公式，根据静力平衡条件，第i（m＜i＜n）段桩位移应满足式（3）：

式中：Esi是第i段虚土桩的弹性模量；Ai是第i段桩的截面积，Ai=πRi2，各个虚土桩段的半径R由式（2）确定；fsi是第i段桩周单位摩阻力，满足式（4）：

式中：λi为第i段桩弹性剪切刚度系数，且λ=τsui/Sui.τsui和Sui分别为第i段桩的极限侧摩阻力和相应的极限位移，由原位静载试验获得.

由各桩段分界面的轴力和位移的连续性条件，可以得到式（5）：

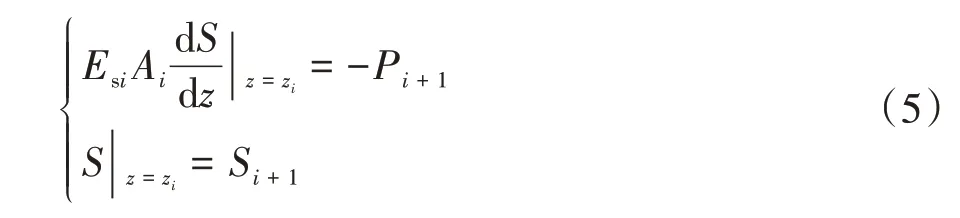
式中：Pi+1为第i+1 段桩桩顶轴力；Si+1为第i+1 段桩桩顶位移；zi为第i段桩底面到桩顶的距离，即各段桩的埋深.

第i段桩桩顶轴力和位移可由式（6）求解得到：

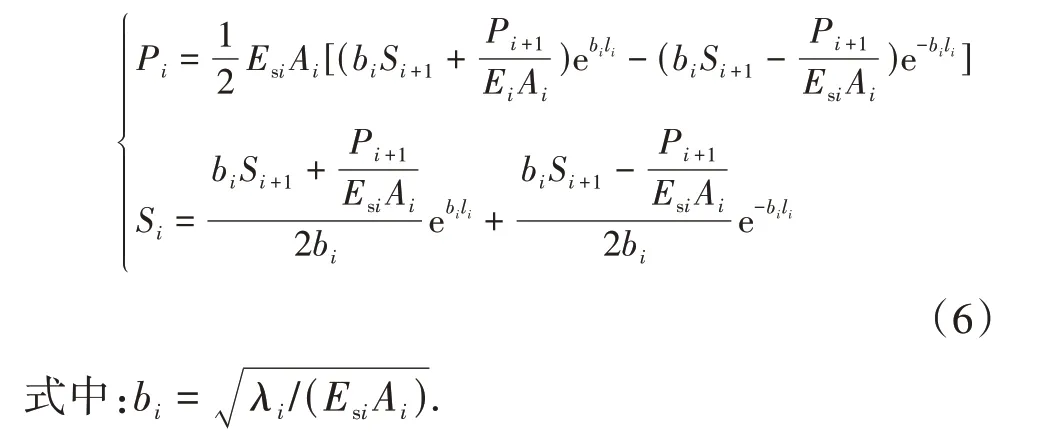
进一步，由式（7）可得第i段桩桩顶刚度为：

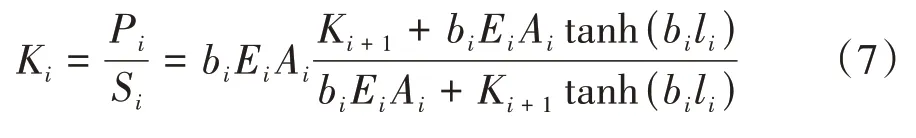
由虚土桩端不发生变形，可以得到：

式（7）（8）组合可以得到第n段桩桩顶刚度：

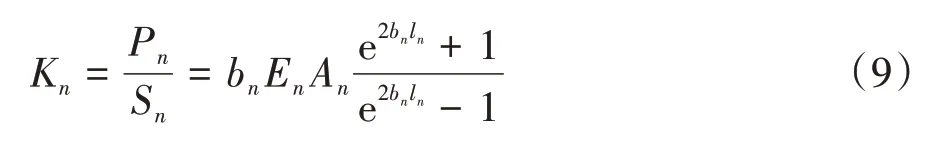
根据上述推导，完整的基桩沉降预测流程可分为以下10个步骤：

1）将桩-土体系划分为n段，如图3所示；

2）假设第n段虚土桩的压缩位移为Sn，则第n段虚土桩的轴力Pn可通过式（9）计算；

3）利用式（6）可递归得到每段虚土桩截面顶部的轴力和位移，实体桩端的轴力和位移等于虚土桩桩顶的轴力和位移；

4）假设第m段实体桩的压缩位移为Scm，并将第m段实体桩桩顶位移值(Sm+1+Scm/2)代入式（1），就可得到第m段实体桩的桩周摩阻力τsm；

5）利用式（10）计算第m段实心桩的轴力增量Pcm：

式中：lm是第m段实体桩的长度，Um是第m段实体桩的截面周长，Um=2πr0，r0是实体桩的半径；

6）利用式（11）计算第m段桩的桩身压缩S′cm：

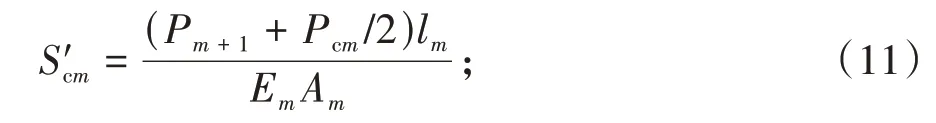
7）将第m段实体桩更新后的压缩位移和步骤4）中的压缩位移Scm值比较，如果与Scm之差不在允许公差（如1×10-6）内，用替换Scm，然后重复步骤4）到步骤6），直到两者之差位于允许公差范围内；

8）将计算得到的位移增量Scm和轴力增量Pcm代入式（12），得到第m段实体桩顶部的轴力Pm和位移Sm：

9）对于第i段实体桩，重复步骤4）到步骤8），得各实体桩桩顶轴力Pi和位移Si，直至得到第1段桩桩顶轴力（即桩顶竖向荷载）P1和位移S1；

10）假定一组递增的第n段虚土桩压缩位移为Sn，然后重复步骤2）到步骤9），便可得到一系列荷载位移值，最终得到桩顶荷载沉降曲线.

3 计算模型参数讨论

桩端土体的沉降对桩顶沉降有较大的贡献，为了突出分析端应力扩散效应对桩顶沉降的影响，下面分析中取单层均质地基，着重对泡形虚土桩模型参数进行讨论，对于成层地基情况，只需要根据实际土层情况进行赋值即可.假定桩土体系参数取值为：实体桩长L1=20 m，桩身半径r0=0.5 m，桩身弹性模量Ep=3×104MPa.地基土层为均质硬黏土层，土层的极限侧摩阻力τsui=120 kPa，相应的极限位移sui=8 mm.土层的双曲线模型计算参数a=0.03 mm/kPa，b=0.007/kPa，c=10 kPa.模型参数是参考本文工程案例的实际参数选取的合理近似值.

3.1 竖向附加应力σz

竖向附加应力σz是采用应力泡形虚土桩模型分析单桩沉降的一个重要参数，选取不同桩端土体的竖向附加应力σz代表选取了不同长度（深度）的泡形虚土桩模型，进一步将竖向附加应力σz和任意深度值z代入式（2）进行数值求解可以得到不同深度处的径向宽度.不同边界的应力泡形虚土桩模型如图4所示，基于本文计算方法竖向附加应力σz对桩顶沉降的影响如图5所示.

图4 不同边界的应力泡形虚土桩模型Fig.4 Stress-bubble fictitious soil-pile model with different boundaries

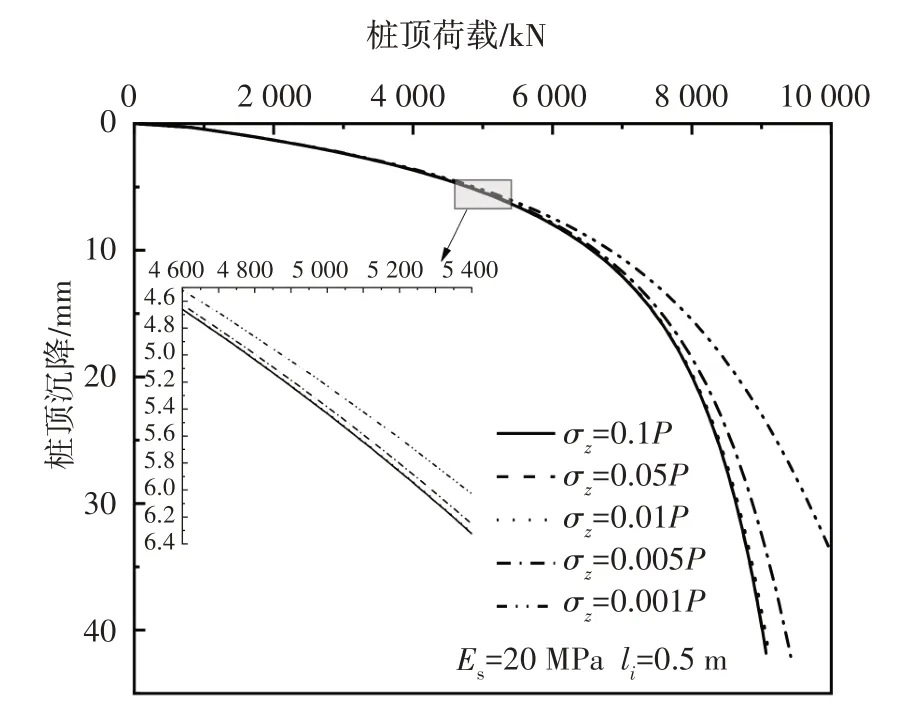
图5 竖向附加应力对桩顶沉降的影响Fig.5 Influence of vertical additional stress on the settlement of pile top

从图5 可以看出当桩顶荷载较小（P1＜5 000 kN）时，桩端竖向附加应力σz对桩顶沉降影响很小，这是由于当桩顶荷载较小时传递到桩端的基底压力和桩端土体中的竖向附加应力相应较小，使得不同竖向附加应力对应的泡形虚土桩产生的压缩变形差值就会很小；当桩顶荷载继续增大时，其对桩顶沉降的影响程度会明显增加，相同荷载下随着桩端竖向附加应力的减小桩顶沉降值随之减小，这是由于竖向附加应力的减小意味着泡形虚土桩的边界增大，即承受基底压力的受荷土体体积增大，那么整体的桩端土体沉降值会减小，桩顶沉降也随之减小；另外随着竖向附加应力的增大，桩顶沉降增大的幅度不断减小并且最后收敛于σz=0.01P附近，因此，在利用应力泡形虚土桩模型进行单桩沉降计算时建议桩端竖向附加应力取值范围在0.005P～0.05P较为合理.

3.2 虚土桩分段精度

进一步讨论虚土桩的分段精度对桩顶沉降计算的影响.本文中虚土桩分段精度用虚土桩分段厚度li来进行量化分析，基于本文计算方法虚土桩分段厚度li对桩顶沉降的影响如图6所示.

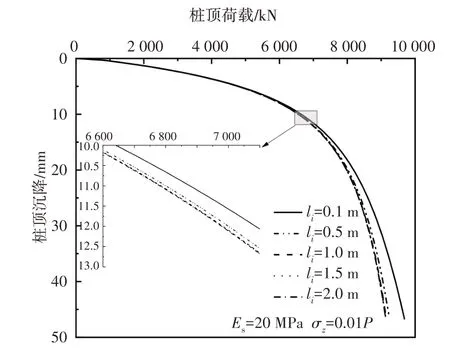
图6 分段精度对桩顶沉降的影响Fig.6 Influence of sectional precision on the settlement of pile top

从图6 可以看出，当桩顶荷载较小（P1＜6 000 kN）时，虚土桩分段精度li对桩顶沉降影响很小；随着桩顶荷载的增大虚土桩分段精度li对桩顶沉降影响增加，并且随着分段精度li的增大，其对桩顶沉降影响幅度不断减小并且最后收敛于li=1 m 附近，因此，在利用应力泡形虚土桩模型进行单桩沉降计算时建议虚土桩分段精度li取值在0.5～1.5 m较为合理.

3.3 虚土桩弹性模量

利用土体弹性模量Es的变化分析桩端土体性质对桩顶沉降的影响，基于本文计算方法桩端土体弹性模量Es对桩顶沉降的影响如图7所示.

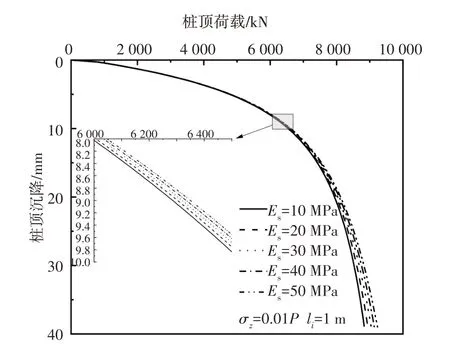
图7 桩端土弹性模量对桩顶沉降的影响Fig.7 Influence of elastic modulus of pile tip soil on the settlement of pile top

从图7 可以看出，当桩顶荷载较小（P1＜6 000 kN）时，桩端土弹性模量Es对桩顶沉降影响很小；随着桩顶荷载的增大桩端土弹性模量Es对桩顶沉降影响程度增加，具体表现为桩端土弹性模量Es越大，桩顶沉降量越小，这是因为桩端土弹性模量Es越大表示桩端土体性质越好，抗压缩变形能力越强，因此整体桩身沉降量会减小.

4 工程实例分析

为了验证本文所述基桩沉降计算方法的准确性，利用本文计算方法对文献［28］中的1 号试桩进行沉降计算，将计算结果与文献［28］中的实测曲线进行比较以验证本文计算方法的合理性，并进一步利用本文计算方法对竖向受荷桩进行沉降性状分析.

试验场地地势平坦，地基土层主要由冲洪积相的亚黏土、黏土、粗砂组成.1 号试桩的实测桩径为1.09 m，桩身弹性模量Ep为2.43×104MPa，桩长为25 m，桩端持力层为粗砂层，根据文献［28］的实测数据，粗砂层的极限侧摩阻力为183 kPa，相应的极限位移为11.6 mm，粗砂层的弹性模量Es取35 MPa.试桩的桩侧各土层双曲线模型计算参数如表1 所示，模型计算参数是赵明华等［20］根据文献［28］的实测数据拟合得到的.

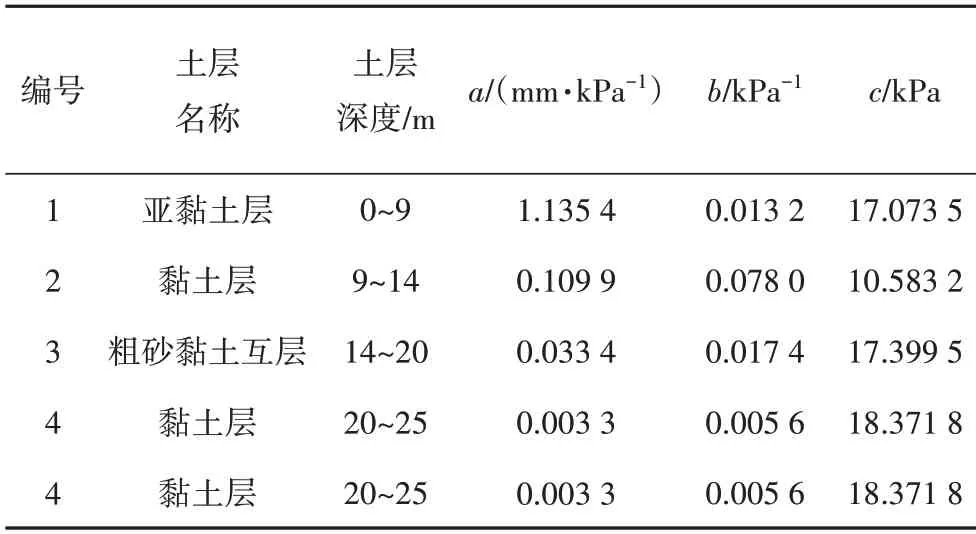
表1 桩侧各土层双曲线模型计算参数Tab.1 Calculate parameters of hyperbolic model of each soil layer at pile side

根据前文计算模型参数讨论分析，在利用本文计算方法计算1 号试桩桩基沉降时竖向附加应力取0.01，虚土桩分段厚度lsi取0.5 m，可以满足计算精度要求.图8 即是利用本文计算方法所得结果与文献［28］中的实测数据的比较图示，计算结果包括桩顶沉降曲线、桩端沉降曲线以及桩身压缩曲线.

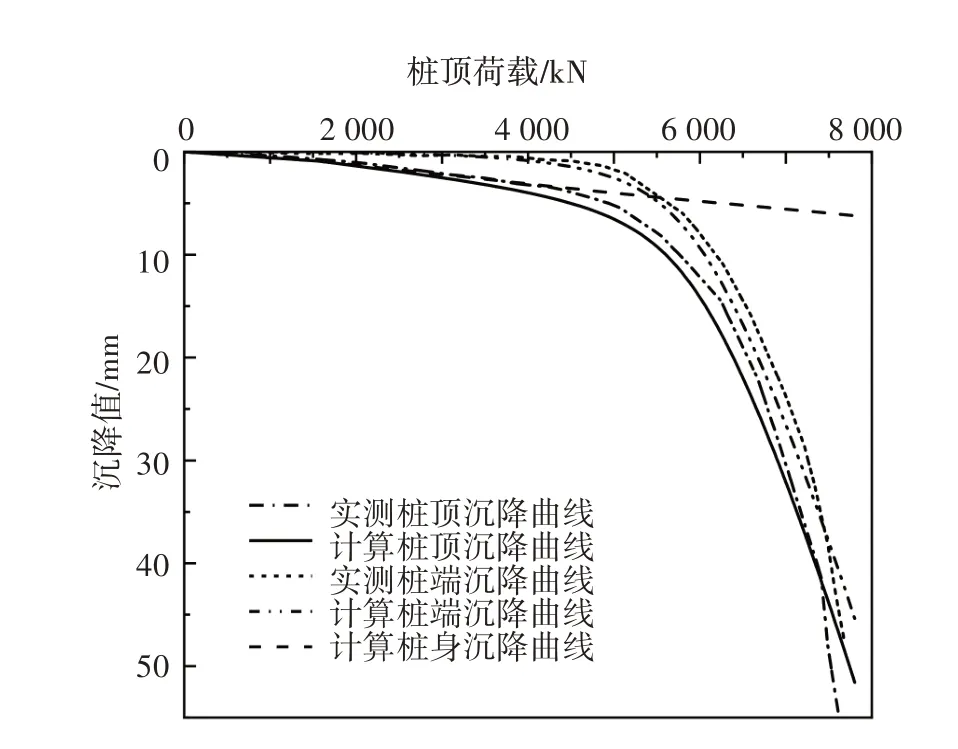
图8 荷载-沉降曲线对比Fig.8 The comparison of load settlement curve

从图8 可以看出，利用本文计算方法所得到的桩顶沉降曲线和桩端沉降曲线与文献［28］中的实测曲线有较好的一致性，说明本文竖向受荷桩的沉降计算方法是合理可行的，可以满足工程应用的计算精度要求.另外从计算得到的桩端沉降曲线和桩身压缩曲线可以清晰地看出在不同桩顶荷载作用下桩端沉降和桩身压缩对整个桩顶沉降的贡献比重，当桩顶荷载较小时（如P1＜5 000 kN），桩顶沉降主要是由桩身压缩造成，桩端土体的沉降量较小；然而随着桩顶荷载的不断增加，传递到桩端的基底压力随之增加，造成桩端土体的压缩量逐渐增大，直到桩端土体沉降量成为桩顶沉降的主要部分.

图9 和图10 是利用本文计算方法所得到的1 号试桩的桩身轴力分布曲线和桩侧摩阻力分布曲线.从图9 可以看出桩身轴力沿桩身逐渐减小，随着桩顶荷载增加传递到桩端的基底压力随之增加.从图10 可以看出桩侧摩阻力整体上大致随深度不断增加，其中由于第2 层粗砂层不具有黏聚力使得桩侧摩阻力略微减小，相应地，图9 中桩身轴力在第2 层粗砂层中减小幅度变缓.

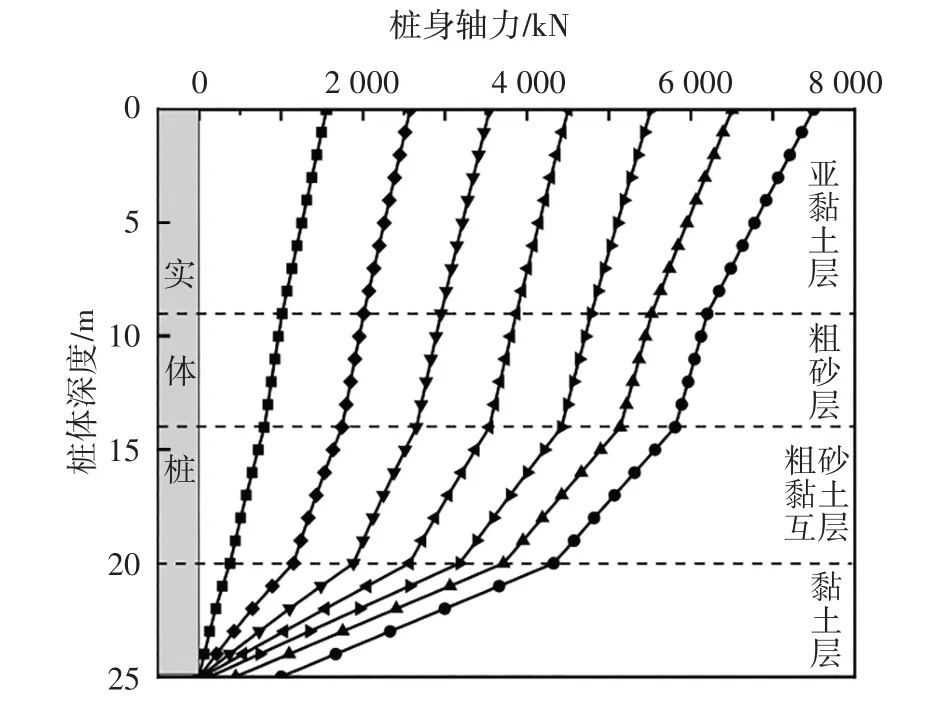
图9 桩身轴力分布曲线Fig.9 The curve of pile axial force distribution

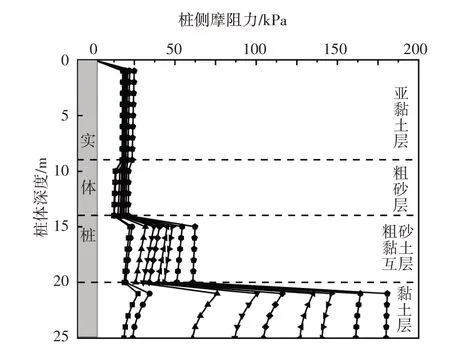
图10 桩侧摩阻力分布曲线Fig.10 The curve of pile lateral friction distribution

5 结论

本文采用应力泡形虚土桩模型和考虑桩土界面初始临界摩阻力的改进双曲线模型，提出了一种可以考虑桩端应力扩散效应和桩土界面初始临界摩阻力影响的竖向受荷单桩沉降简化计算方法.通过将利用本文方法得到的计算结果和实测曲线进行对比，表明本文单桩沉降计算方法是合理可行的.

采用本文提出的单桩沉降计算方法可以严格地给出桩端应力扩散边界，并且进一步直观地分析桩端土体性质变化对桩顶沉降的影响.通过对计算模型参数的分析讨论，在利用应力泡形虚土桩模型进行单桩沉降计算时，建议桩端附加应力在0.005P～0.05P之间取值，虚分段精度在0.5～1.5 m 之间取值较为合理.

利用本文提出的单桩沉降计算方法可以方便地得到桩顶沉降曲线、桩端沉降曲线、桩身压缩曲线以及桩身轴力和桩侧摩阻力分布曲线，对分析研究竖向受荷桩的沉降性状具有重要意义，同时算法参数明确，计算简单，具有广泛的工程应用前景.