对一道2022年全国高考试题的探究与思考
2022-08-19张鹄
张 鹄
(湖北省武汉市第二中学 430010)
孔 峰
(湖北省武汉市教育科学研究院 430022)
2022年高考数学全国乙卷理科第21题是一道函数与导数的压轴题.题设中函数结构简洁明了,是由基本的指数函数与对数函数模型整合而成;设问内容更是司空见惯,是师生常见的切线方程求解和已知零点个数求参数的问题类型.为此,笔者就该题的解答情况对即将进入新高三的学生进行了问卷,发现大部分学生对第(2)问不知从何处入手分析.这让笔者在思考,如何帮助学生透过试题表象找准切入点,进而对“冰冷美丽”的试题进行一番“火热”的思考.下面,以美籍匈牙利裔著名数学家波利亚的“怎样解题”表为指引,开启我们的探究思考过程.
1 基于“怎样解题”表的试题探究
1.1 理解题目
题目1
已知函数f
(x
)=ln(1+x
)+ax
e-,其中a
∈R
.(1)当a
=1时,求曲线y
=f
(x
)在点(0,f
(0))处的切线方程;(2)若f
(x
)在区间(-1,0)和(0,+∞)内各恰有一个零点,求a
的取值范围.问题1
题目1第(2)题是一个什么问题?预设 这是已知函数零点个数求参数范围的问题.
问题2
条件是什么?预设f
(x
)在(-1,0)和(0,+∞)内各有一个零点.1.2 拟定方案
问题3
你以前见过它吗?或者你见过以稍有不同的形式呈现的类似题目吗?你知道与它有关的题目吗?预设 我们见过一道与它类似的题目,即2017年新高考全国Ⅰ卷理科第21题:
题目2
已知函数f
(x
)=a
e2+(a
-2)e-x
.(1)讨论f
(x
)的单调性;(2)若函数f
(x
)有两个零点,求a
的取值范围.问题4
题目2的第(2)题与题目1的第(2)题有关,你能利用题目2的求解方法解答题目1的问题吗?预设 形式上类似.不过,题目1限定了零点存在的区间,即两个断开的区间.
问题5
为什么不把两个区间合成一个区间(-1,+∞)?预设 合成一个区间就暴露了与题目2的联系.命题者也许为了推陈出新,通常会在问题形式上设计新意,但万变不离其宗.
问题6
为什么要在x
=0处将区间断开?这里有没有命题者想要表达而又有所隐藏的信息?能否分析一下?预设f
(x
)在x
=0处的函数值等于0,即0是函数f
(x
)的零点.若把0放在区间内,那就有3个零点,与题意不符.另外,函数f
(x
)在(-1,+∞)上的图象穿过原点,意味着满足题意的图象特征可能如下面图1和图2所示.
图1 图2
问题7
在上面的图象中,你能判断题目1第(2)问对应的图象是哪一个吗?把握函数图象特征一般应从哪些方面进行分析?预设 就本题而言,可以从定义域、值域、单调性、极值以及零点等方面分析.由于f
(0)=0,f
′(0)=1+a
均存在,为使f
(x
)的图象在区间(-1,0)及(0,+∞)上各恰好穿过x
轴一次,函数f
(x
)的变化情况只能如图1和图2所示.为了进一步找到题设函数对应的图象,还可以先动态定性研究较容易的局部图象特征:首先,基于零点附近两侧的函数值要么为正,要么为负.于是,我们不妨先研究x
=0右侧的情况.因为当x
>0时,ln(1+x
)>0,x
e->0,所以,若a
≥0,则f
(x
)>0,与题意不符.从而a
<0.其次,对函数进行求导,得令φ
(x
)=e+a
(1-x
),则对a
<0,借助极限工具可得到:当x
→+∞时,φ
(x
)>0,从而f
′(x
)>0,函数f
(x
)在相应区间上单调递增.这样由局部图象的特征不难推测整体图象的特征,从而,基本确认题目1第(2)问对应的图象为图1.问题8
借助图1,你能分析一下函数f
(x
)在(-1,0)及(0,+∞)上各有一个零点的含义吗?预设 函数f
(x
)在(-1,0)上先增后减,在(0,+∞)上先减后增.这需要函数f
(x
)在两个区间上各有一个极值点.这样,把零点转化为极值点来讨论,体现了数学的转化与化归思想.问题9
你能找到这两个极值点吗?又准备采用什么工具和方法?你之前有过这方面的经验吗?预设 记得之前是这样做的,先对函数求导,若导函数的零点可以直接求出,就接着讨论这些零点附近两侧的导函数符号;若不能,则利用函数零点存在定理将零点限定在适当区间,有时为找到这样的区间,可能还会用到找点技巧如借助函数不等式进行放缩的方法.
分析到这里,我们就可以着手解决问题了.
1.3 实施方案
首先,对函数进行求导,得为分析导函数f
′(x
)的符号,记φ
(x
)=e+a
(1-x
).若a
≥0,则当x
>0时,ln(1+x
)>0,ax
e-≥0,从而f
(x
)>0,与题意不符.若a
<0,则对φ
(x
)求导得,φ
′(x
)=e-2ax
,当x
>0时,因为e单调递增,2ax
递减,所以φ
′(x
)递增,从而φ
′(x
)>φ
′(0)=1>0,因此φ
(x
)在(0,+∞)上递增,φ
(x
)>φ
(0)=1+a
.糖皮质激素和丙种球蛋白对暴发性心肌炎的治疗安全性和有效性良好,建议所有暴发性心肌炎患者尽早使用[1]。免疫调节剂输注时护理人员需谨慎给药。丙种球蛋白属于高张液体,静脉滴注时,需先确保静脉通路安全通畅。由于大剂量使用该药可增加心室前负荷,加重心力衰竭,所以必须在24小时内缓慢输注[3]。输液过程中,严密观察输液血管状况,发现液体外渗、过敏及心力衰竭症状加重时,立即处理。使用大量甲泼尼龙可能引起消化道应激性溃疡,骨质疏松及精神神经异常,水电解质失衡,建议每日检查血电解质[6],遵医嘱使用护胃抑酸药物,且密切观察有无消化道出血症状[3]。
若-1≤a
<0,则φ
(x
)≥0,f
′(x
)>0,故f
(x
)在(0,+∞)上递增,f
(x
)>f
(0)=0,也与题意不符.若a
<-1,则φ
(0)<0,φ
(1)>0,而φ
(x
)在(0,+∞)上递增,故由函数零点存在定理知,在(0,+∞)上存在唯一x
∈(0,1),使φ
(x
)=0.当x
∈(0,x
)时,φ
(x
)<0,即f
′(x
)<0;x
∈(x
,+∞)时,φ
(x
)>0,即f
′(x
)>0,所以f
(x
)<f
(0)=0.又x
<1+x
x
=e-,则f
(e-)>ln(1+e-)+a
>ln e-+a
=0,从而存在唯一x
∈(x
,e-),使f
(x
)=0,即f
(x
)在(0,+∞)上恰有一个零点x
.由=1>0,φ
′(x
)=e-2ax
在(-1,0)上递增,则存在唯一x
∈(-1,0),使φ
′(x
)=0.当x
∈(-1,x
)时,φ
′(x
)<0,φ
(x
)递减;当x
∈(x
,0)时,φ
′(x
)>0,φ
(x
)递增.故φ
(x
)<φ
(0)=1+a
<0,而φ
(-1)=e>0,由函数零点存在定理知,存在唯一x
∈(-1,x
),使φ
(x
)=0.当x
∈(-1,x
)时,φ
(x
)>φ
(x
)=0,f
′(x
)>0,f
(x
)递增;当x
∈(x
,x
)时,φ
(x
)<φ
(x
)=0,f
′(x
)<0,f
(x
)递减;又x
∈(x
,0)时,φ
′(x
)>0,φ
(x
)递增,从而φ
(x
)<φ
(0)<0,f
′(x
)<0.即x
∈(-1,x
)时f
′(x
)>0,f
(x
)递增;x
∈(x
,0)时,f
′(x
)<0,f
(x
)递减;且x
∈(x
,0)时,f
(x
)>f
(0)=0.所以f
(x
)>f
(0)=0.又对求导,得从而在(-1,0)上递增,所以又ln(1+e3-1)=3a
,所以f
(e3-1)<3a
+(-a
e)=a
(3-e)<0,由函数零点存在定理知存在唯一x
∈(e3-1,x
),使f
(x
)=0.综上可得,a
<-1.1.4 回顾
问题10
你能检验一下这个结果吗?有没有直观的验证方法?预设 能.画出函数f
(x
),φ
(x
),φ
′(x
)的图象,并结合图3~图5进行分析验证发现上述过程正确.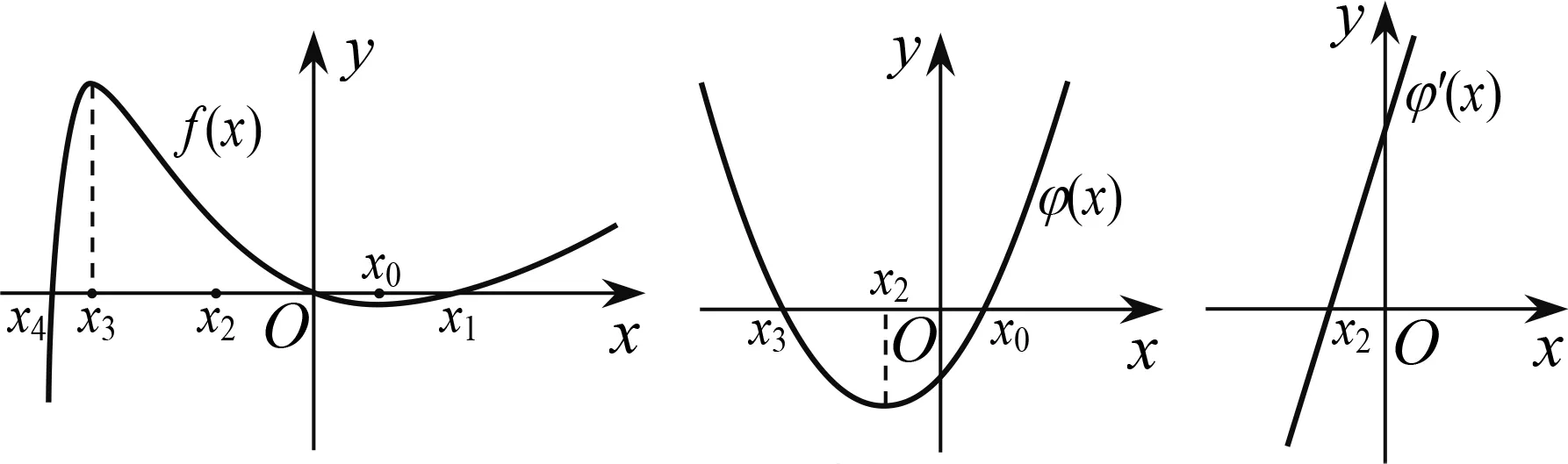
图3 图4 图5
问题11
你能结合图象给出新的方法吗?若a
≥0,则当x
∈(-1,0)时,φ
(x
)>0,f
′(x
)>0,f
(x
)递增,f
(x
)<f
(0)=0,f
(x
)在(-1,0)内无零点,不符合题意.若-1≤a
<0,则当x
>0时,φ
′(x
)>0,φ
(x
)递增,φ
(x
)>φ
(0)=1+a
≥0,即f
′(x
)>0,f
(x
)递增,从而f
(x
)>f
(0)=0,f
(x
)在(0,+∞)内无零点,不符合题意.若a
<-1,则又φ
′(x
)=e-2ax
在(-1,0)上递增,从而存在唯一x
∈(-1,0),使φ
′(x
)=0.当x
∈(-1,x
)时,φ
(x
)递减;当x
∈(x
,0)时,φ
(x
)递增.又a
<0,所以存在唯一x
∈(-1,x
),使φ
(x
)=0.当x
∈(-1,x
)时,φ
(x
)>0,f
′(x
)>0,f
(x
)递增;当x
∈(x
,x
)时,φ
(x
)<0,f
′(x
)<0,f
(x
)递减;x
∈(x
,0)时,φ
(x
)<φ
(0)<0,f
′(x
)<0,f
(x
)递减,即x
∈(x
,0)时,φ
(x
)<0,f
′(x
)<0,f
(x
)递减,从而f
(x
)>f
(0)=0.易知在(-1,0)上递增,从而又a
<-1,则所以f
(x
)a
e).令ln(1+x
)-a
e<0,则x
f
(ee-1)<0,由函数零点存在定理知,在(ee-1,x
)上存在唯一x
,使f
(x
)=0.当x
∈(0,+∞)时,φ
(0)=1+a
<0,φ
(1)=e>0,而φ
(x
)=e-a
(1-x
)在(0,+∞)上递增,由函数零点存在定理知,在(0, +∞)上存在唯一x
∈(0,1),使φ
(x
)=0.当x
∈(0,x
)时,φ
(x
)<φ
(x
)=0,即f
′(x
)<0,f
(x
)递减,故f
(x
)<f
(0)=0.当x
∈(x
,+∞)时,φ
(x
)>φ
(x
)=0,即f
′(x
)>0.又x
<1+x
x
=e--1>1,则f
(e--1)>ln(1+e--1)+a
=0,从而存在唯一x
∈(x
,e--1),使f
(x
)=0,即f
(x
)在(0,+∞)上恰有一个零点x
.综上,a
<-1.问题12
你能借助图象从新的角度解释题设条件的含义吗?预设 所谓函数f
(x
)的零点,就是函数f
(x
)的图象与x
轴交点的横坐标.有时为便于利用图象寻找交点,也可以转化为两个函数的图象之间的交点问题.因此,分别构造函数g
(x
)=ln(1+x
),h
(x
)=-ax
e-,再画出这两个函数的图象(图6).可以看出,除原点外,这两个函数图象若还能再有两个交点,需要考虑原点附近图象特征及变化趋势.从而又转化为两个函数在原点处的切线斜率-a
与1的大小比较,结合图象不难得到,当-a
>1即a
<-1时,满足题意.
图6 图7
问题13
你还能借助图象从切线的角度再次给出恰有两个零点的新的解释吗?预设 构造两个新的函数m
(x
)=eln(1+x
)及y
=-ax
.f
(x
)在(-1,0)和(0,+∞)上各有一个零点⟺方程eln(1+x
)=-ax
在区间在(-1,0)和(0,+∞)内各有一个实根(图7).由m
(x
)=eln(1+x
),知令则当-1<x
<0时,t
′(x
)<0,t
(x
)递减;当x
>0时,t
′(x
)>0,t
(x
)递增.所以t
(x
)>t
(0)=1>0,m
′(x
)>0,m
(x
)在(-1,+∞)上递增.又x
≥0时,e≥1,所以m
′(x
)≥1.又m
′(0)=1,所以m
(x
)在(0,0)处的切线方程为y
=x
.记n
(x
)=m
(x
)-x
=eln(1+x
)-x
,则因为1+x
≤e,所以x
>0时,n
′(x
)>0,n
(x
)>n
(0)=0,即eln(1+x
)>x
.又则当x
>0时,m
″(x
)>0,m
(x
)为下凸函数.当-1<x
<0时,令则递增,x
→-1时,r
(x
)→ -∞;x
→0时,r
(x
)→1,所以存在唯一α
∈(-1,0),使r
(α
)=0,且x
∈(-1,α
)时,r
(x
)<0,m
″(x
)<0,m
(x
)为上凸函数;x
∈(α
,0)时,r
(x
)>0,m
″(x
)>0,m
(x
)为下凸函数.又x
→-1时,时,故y
=m
(x
)与y
=x
仅在(-1,0)内有一个公共点,从而要使f
(x
)在区间(0,+∞)上恰有一个零点,则-a
>1,即a
<-1.又a
<-1时,y
=m
(x
)与y
=-ax
在(-1,0)上也有一个交点,因此,a
<-1为所求.问题14
你能对上面的探究过程作个总结吗?预设 借助函数图象进行直观分析,从局部入手,把握特殊点、关键点处函数性态的刻画,然后再拓展到整体全面的分析判断.
2 若干思考
2.1 借助波利亚“怎样解题表”解题
“怎样解题表”的4个步骤和程序组成了一个完整的解题教学系统.当我们对一个比较难的高考导数压轴题按照波利亚“怎样解题表”进行解答时,会发现在由浅入深的问题串引导下,能够让分析逐渐进行下去直至顺利完成解答过程.因此,我们需要加深对波利亚“怎样解题表”的理解和掌握.
2.2 多角度深入研究高考试题
高考全国卷导数压轴题尽管年年求新求异,但我们透过近几年试题仍然可以发现,高考命题的原则是整体稳定,适度创新.命题始终围绕导数部分的主线内容,聚焦学生对重要数学概念、定理、方法、思想的理解和应用,强调基础性、综合性;注重数学本质、通性通法,淡化解题技巧,突出数学学科核心素养的考查.
在高三复习备考教学中,要深入研究近几年高考试题,并对其作系统全面的梳理与研究,把握试题的变化趋势,挖掘高考试题的潜在功能价值;积极引导学生从知识的本质出发,对导数压轴题进行多角度剖析;运用函数图象等直观想象分析工具,对定义区间边界点或区间内特殊点附近的图象进行微观分析,利用局部到整体、特殊到一般等思想方法多角度领悟题目的隐含条件,充分暴露命题意图,简化思维过程,优化解题方法,降低运算难度.从而在分析问题的过程中提升学生的直观想象、逻辑推理等学科核心素养.
