基于遗传算法的钻井液流变参数计算及模式优选
2022-08-18朱朋震王越支李明亮
朱朋震,王越支,刘 洋,李明亮
1.长江大学石油工程学院,湖北武汉430000;2.中国石油西南油气田分公司川东北气矿,四川达州635000 3.中海石油(中国)有限公司天津分公司,天津300452
对于窄安全密度窗口地层,钻进过程中需要精确控制井筒当量循环密度(ECD),确保井筒压力平衡,规避井下溢漏事故。钻井液流变参数的准确计算和流变模式的优选是当量循环密度计算的前提[1]。准确的流变参数计算可用于优选钻井排量,达到控制井筒当量循环密度的目的,使钻头顺利穿过压力风险区域,避免事故后的时间成本与资金成本,从而实现钻井的降本增效。
为了准确表征钻井液的流变性,需要选择恰当的流变模型和准确的流变参数。目前,行业内钻井液流变参数的确定方法主要包括经验法、线性最小二乘法[2]以及非线性回归法[3]3种。其中,经验法和线性最小二乘法易于实现,常为现场选用,但是其计算精度有待提高;非线性回归法计算精度较高,但是其过分依赖初始值条件,容易出现不收敛或局部最优的情况,导致通用性不足。随着新兴智能算法的普及,对于多种不同钻井液流变模型,结合智能算法,找到一种流变参数通用计算方法成为现实。本文根据六速黏度计读数,基于遗传算法,建立不同流变模式下的流变参数通用计算模型,并通过比较相关系数,建立流变模型优选方法。
1 流变参数常规算法
钻井液流变性的核心问题就是研究各种钻井液体系的剪切应力与剪切速率之间的关系。流变模式(流变方程)即是用来表示二者之间关系的数学方程式[4],其中的流变参数是流变模式用来确定剪切应力与剪切速率之间关系的关键参数。目前,剪切应力和剪切速率通常用范氏六速旋转黏度计(六速黏度计)确定,壁面剪切速率与剪切应力的关系[5]见式(1)和(2)。

式中:γ为剪切速率,s-1;N为黏度计转速,r/min;τ为剪切应力,Pa;θ为黏度计读数,mPa·s。
1.1 经验公式
经验公式是利用黏度计部分读数通过相应的计算公式直接计算流变参数。常用流变模式主要包括宾汉模式和幂律模式,其相应的流变参数计算公式如表1所示。此方法不需要全部六速黏度计测量数据,且计算简单,易于现场实施,常为现场选用。

表1 不同流变模式下流变参数的计算
1.2 线性回归法
回归分析是表征各变量间相关关系的数学方法,线性回归因其简单且具有代表性常用来回归流变参数。对流变模式进行线性回归计算,需要将流变方程转化为线性形式,即τ̂=â+b̂γ,变换后的宾汉模式和幂律模式回归模型如表2所示。

表2 不同流变模式回归模型
2 遗传算法
遗传算法(GA)[6-7]是由Holland教授于1975年提出的,它采用达尔文进化思想,模仿自然界生物遗传进化过程中“物竞天择、适者生存”的原理,是一种全局优化随机搜索算法。相对于其他寻优算法,遗传算法搜索从群体出发,具有潜在的并行性、可以方便地进行分布式计算、加快求解速度等优点,可以进行多个个体同时比较;使用概率机制进行迭代,具有随机性,避免局部最优,因此选用该算法作为钻井液流变参数计算的方法。
2.1 遗传算法步骤
遗传算法的主要步骤包括:①确定算法优化的目标函数;②将目标函数代入算法,建立初始种群,对种群进行选择、交叉和变异操作,反复迭代;③把在任一代中出现的最好的个体串作为问题的满意解或最优解。
简单遗传算法流程如图1所示,其中GEN代表当前代数。

图1 简单遗传算法流程
2.2 染色体编码与解码
经典遗传算法中使用“染色体”来代指个体,它是由二进制串组成的,它的每一维称为一个基因,取值为0或者1对优化问题解空间进行编码,编码的长度取决于自变量的范围(准确来讲应该是决策变量的范围)和搜索精度。简单来说,就是DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表型到基因型的映射,反之,解码就是从基因型到表型的映射。
2.3 适应度函数
遗传算法中以个体适应度的大小来评定各个个体的优劣程度,从而决定其遗传机会的大小。假设实测数据为(γ1,τ1)(γ2,τ2)……(γm,τm),其中m为实测数据个数。为找到适合的参数使拟合出的模式曲线与实测数据达到最好的效果,可对两种流变模式分别构造最小二乘法目标函数作为适应度函数,见表3。

表3 不同流变模式下的最小二乘法目标函数
根据最小二乘法的思想求取流变参数,可归结为求取上述目标函数的最小值问题[2],即M=minf(μp,τ0)或M= minf(K,n)。
2.4 遗传算子
1)选择操作:根据达尔文的进化论,对生存环境适应程度比较高的物种特性将有极大可能传递给下一代,而对于那些适应环境程度低的物种多半被自然界所淘汰。
2)交叉操作:遗传算法中的交叉运算是指群体中的各个个体随机搭配成对,搭配成对的两个染色体相同的位置切断之后以交叉组合的方式交换基因,进而形成一个新的个体。交叉组合的方式是遗产算法中的重要性质,在算法中发挥重要作用。
3)变异操作:对群体中的每一个个体,在基因复制过程中产生了某些意外(外部环境),发生变异产生新的染色体,从而表现出新的性状。
2.5 流变模式优选
流变模式的优选,不仅对于确定钻井液流变参数、表征钻井液实际流变性至关重要,而且还对钻井液性能评价、钻井水力参数优选、保持井壁稳定等均有显著作用[8]。常用的流变模式优选方法包括流变曲线对比法、剪切应力误差对比法和相关系数法[9]。其中,流变曲线对比法取决于决策者的直观判断,但肉眼判断困难;剪切应力误差对比法易受异常点干扰;相关系数法表示计算值与实测值之间的拟合程度,相关系数越接近于1,拟合效果越好,可用式(3)表示。

3 计算实例
使用六速黏度计实测钻井液不同转速下的黏度,结果见表4。使用表4中钻井液实测参数对各钻井液流变模式进行线性拟合,得到对应流变模式的流变参数及回归系数R,结果见表5。

表4 钻井液不同转速下的实测黏度
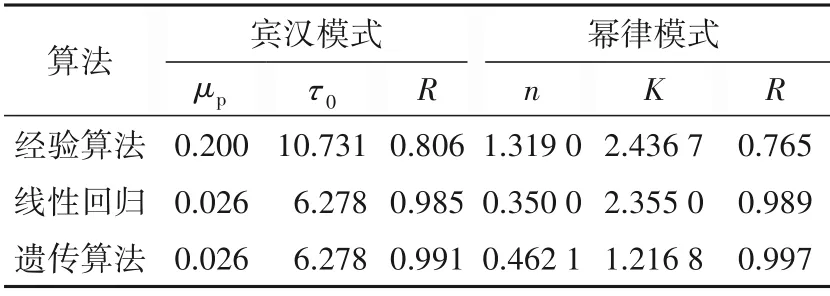
表5 不同流变模式中参数计算结果
使用MatLab进行遗传算法迭代计算,群体大小设定为50,交叉概率为0.8,变异概率为0.005,终止代数50,结果如图2所示。
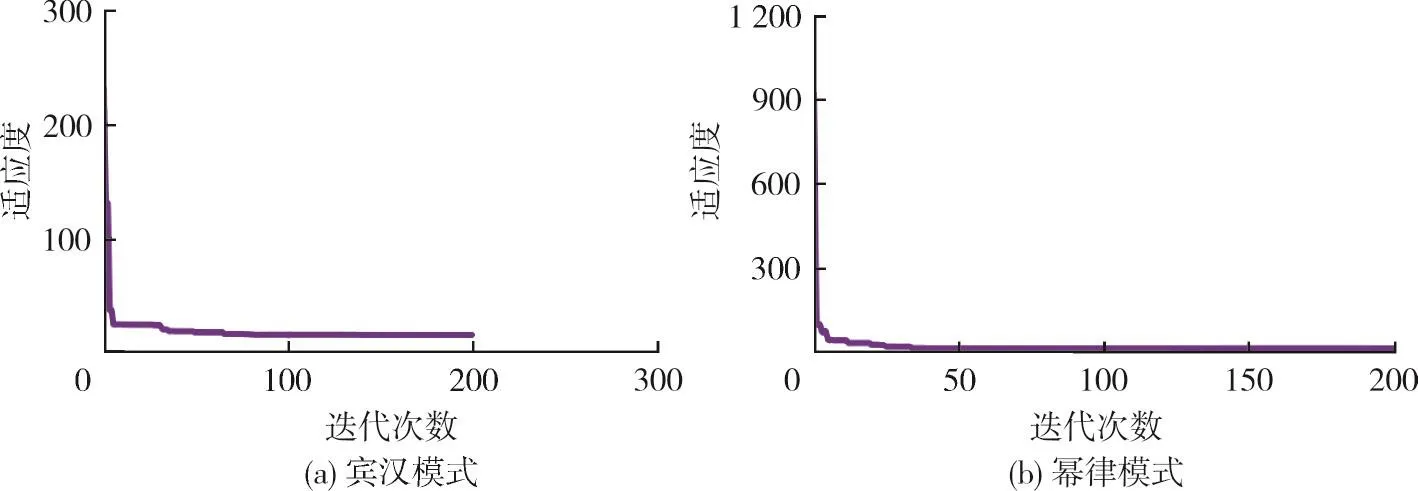
图2 基于遗传算法的钻井液流变参数优化过程
由图2可以看出:遗传算法的收敛速度很快,而且随着迭代次数的增加,两种模式下解的适应度均逐渐向理想值靠近,宾汉模式迭代65次之后适应度变化很小,幂律模式迭代35次之后适应度变化很小,可以认为遗传算法已经找到了最优解,即求出了流变参数的最优值。将遗传算法得到的各流变参数代回流变方程并与传统算法进行比较,结果见表5。由表5中相关系数可知:幂律模式较宾汉模式更适合描述钻井液流变模式。
将表5中遗传算法结果代入各流变模式,得到两种流变模式的拟合效果,结果见图3。由图3可知:遗传算法对各模式流变参数的计算较经验算法更为准确,特别是在非线性模式(幂律模式)下,对比于线性回归法有不可比拟的优势。

图3 基于遗传算法的各流变模式拟合效果
4 结论
1)对于一些非线性拟合,可以转为线性拟合,如采用最小二乘法的拟合流变参数,但是其计算结果的精度可能不够高,且线性拟合参数可能没有良好的统计性质。
2)在钻井液流变模式参数优选方面,遗传算法不但能显著提高流变模式参数的计算精度,而且对非线性流变模式(幂律模式)更具优势。
3)幂律模式较宾汉模式更适合描述钻井液流变模式。
