基于GSA-ELM 算法的股票市场预测模型

张小宁，官启航，黄敬宇

（1.甘肃广播电视大学，甘肃 兰州 730000；2.兰州大学信息科学与工程学院，甘肃 兰州 730000）

1 研究背景

股票市场的指数高低是反映国内市场经济发展情况的重要指标之一[1]。随着国内人民经济生活水平的不断提高，参与股票投资的人数也逐年增长。股票市场因其具有高风险与高收益并存的特点，一直是人们的主要投资工具。因此，如何对股票的价格走势进行有效地预测，进而提高股票的投资回报率，也成为了众多投资者所关注的问题[2]。

股票市场的波动预测是多种因素共同作用的结果，主要有国家出台的金融政策、发售股票的公司主体的经营情况和国家汇率的调整等因素[3]。众多因素的变化使得股票市场价格波动频繁，同时也具有了非线性、稳定性、随机性等特点。近年来深度学习技术的飞速发展，并应用于各种领域，都取得了较好的成果。因此，诸多学者将深度学习的技术和预测股票市场的价格走势相融合，通过模型进行预测，以此来降低股民的投资风险，提高股票的经济收益[4]。

2 国内外研究现状

股票市场的预测通常是利用前期的股票数据，来预测股票未来价格走势的过程[5]。经过国内外学者的深入研究，股票市场的预测主要分为基于传统机器学习算法和基于深度学习网络两种方法。

传统的机器学习算法主要包括支持向量机、K近邻算法和XGBoost 算法。Trafails 和Ince[6]将支持向量机技术应用于RBF 神经网络和反向传播过程中，并利用生成的模型去预测股票的价格走势。Cao和Tay[7]提出了一种自适应参数的改进支持向量机算法，来应对金融时序序列的稳定性，并将模型应用在海外股票市场的数据集中，结果表明支持向量机的性能较高。张伟楠等[8]利用K 近邻算法来预测股票市场价格的涨跌，集成多个K 近邻算法模型，通过滑窗方法将历史价格和当前价格进行对比，结果表明集成模型能有效预测股票价格的波动情况。凌筱玥[9]利用XGBoost 算法运算效率高和准确率高等优点，对上证综合指数数据集进行股票价格的涨跌预测，同时和支持向量机、决策树算法进行对比分析，结果表明基于XGBoost 算法的预测准确率更高。

基于深度学习网络的股票预测方法能够在数据量较多的情况下，通过自身的特征提取和表示能力，在不考虑经济学原理的前提下直接从数据中提取出有效信息[10]。Chen 等[11]利用LSTM 网络对国内股票市场的历史数据进行分析，相比于随机预测方法，LSTM 网络的预测精确度更高。Shao 等[12]先利用K-means 算法对股票数据进行聚类集群，根据集群的数量，对每一个集群分别进行LSTM 网络训练，来预测下一个股票加一日的价格。Althelaya 等[13]提出将双向长短期记忆神经网络（BiLSTM）应用于股票市场的指数预测中，同时和堆叠长短期记忆神经网络（SLSTM）和长短期记忆神经网络（LSTM）对比，结果表明BiLSTM 的模型预测精确度更高。

本研究主要利用股票市场交易的历史数据作为基准，利用引力搜索优化ELM 网络，对未来的股票市场进行回归预测分析，并通过实际的交易数据进行误差计算，来衡量回归预测模型的性能。

3 相关技术知识

3.1 引力搜索算法

引力搜索算法（Gravitational Search Algorithm,GSA）属于群智能优化算法，是伊朗的Rashed 等[14]受到万有引力理论的启发而提出的。算法的基本原理是在解空间中的个体都会互相吸引，其吸引力的大小和个体的质量乘积成正比，和个体间距离的平方成反比[15]。个体的移动遵循质量小的个体会向质量大的个体的方向去移动原则，经过算法不断地迭代，质量最大的个体即为优化问题的最优解。引力搜索算法的数学过程如下。

假设算法中的搜索空间有n 维，个体的种群规模为X=（X1，X2，...，Xn），其中第i 个个体在每个维度上的位置信息可表示为Xi=（x1，x2，...xn）。算法初始化时，每个个体的位置是随机分布的，t 时刻下，空间中个体i 和个体j 的引力大小如下：

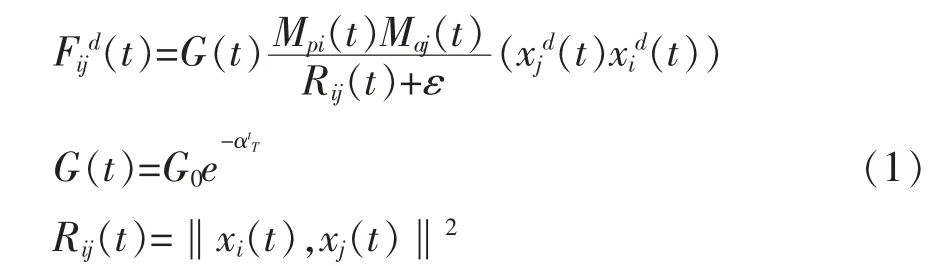
式中：Mpi（t）表示个体i 的质量大小；Maj（t）表示个体j 的质量大小；ε 是无限接近于0 的数，防止分母为0；G（t）是引力参数，随着t 的增加而减小；G0和α 是常数；T 为最大迭代次数；Rij（t）表示个体i 和个体j 之间的欧氏距离的平方。

t 时刻下，个体i 在维度d 上的所有作用力的合力大小和产生的加速度大小如下：

式中：rand 是[0，1]之间的随机数；Mi（t）表示个体i 的质量大小。在引力搜索算法中，kbest（t）是随时间增加而减小的线性函数，由于算法存在陷入局部最优的缺陷，故随着迭代次数的增加，算法应该更加注重开发能力，探索能力逐渐减弱。kbest（t）函数的初始值设为种群规模数量N，在算法的迭代过程中，线性减小至1，表示最终只剩下一个质量最大的个体作用于其他个体。

t 时刻下，个体的质量大小和适应度值大小有关，适应度值大的个体质量也越大，个体i 的质量的计算方式如下所示：

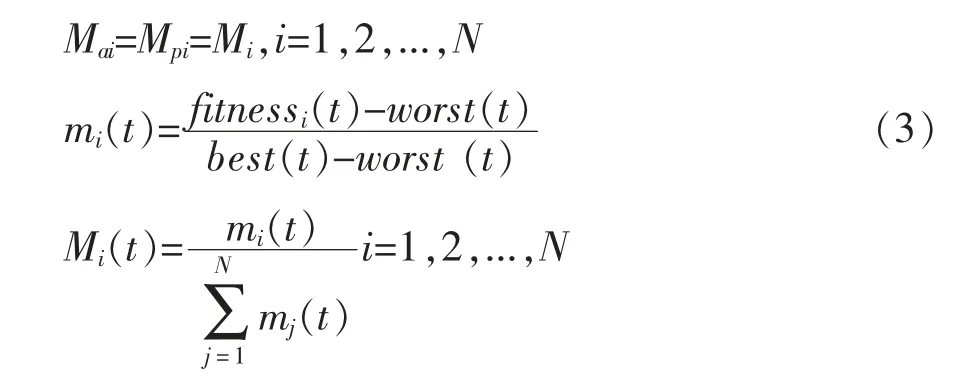
式中：fitnessi（t）是t 时刻下个体i 的适应度值；best（t）和worst（t）表示t 时刻下，所有个体中适应度值最大和最小值。

当待优化问题是求解函数的最小值时，所有个体中适应度值最大和最小值计算方式如下：

当待优化问题是求解函数的最大值时，所有个体中适应度值最大和最小值计算方式如下：

个体i 的移动速度和位置信息的更新方式如下所示：

引力搜索算法的执行步骤如下。

第一步：初始化算法的参数。包括个体的种群规模N，算法最大迭代次数T，并随机初始化个体在空间中的位置信息，设置每个个体的初速度为0；

第二步：计算每个个体的适应度值大小；

第三步：根据公式（3）计算每个个体的质量大小；

第四步：根据公式（2）计算每个个体在不同维度上的所有作用力的合力大小和产生的加速度大小；

第五步：根据公式（6）计算每个个体的移动速度和更新后的位置信息；

第六步：回到第二步重新迭代计算，若达到算法的最大迭代次数，则结束循环，输出结果。

3.2 ELM 网络

极限学习机（Extreme Learning Machine，ELM）是由新加坡南洋理工大学的Huang 等[16]于2004 年提出的一种单隐藏层的前馈神经网络。相比于传统的BP 神经网络，ELM 网络的学习速度更快，需要调节的参数较少，只需初始化隐藏层的神经元结点个数，具有较好的泛化能力[17]。ELM 网络训练时没有通过梯度下降法迭代求解的过程，而是利用输入层和隐藏层的权值矩阵和实际输出矩阵来进行求解，故ELM 网络训练的时间更短[18]。ELM 网络结构图如图1 所示，组成包括一个输入层、一个隐藏层和一个输出层。

图1 ELM 网络结构图

假设样本规模为N，每一个样本可表示为（xi，ti），隐藏层的神经元结点个数为M，激励函数为g（x）的极限学习机表达式如下：

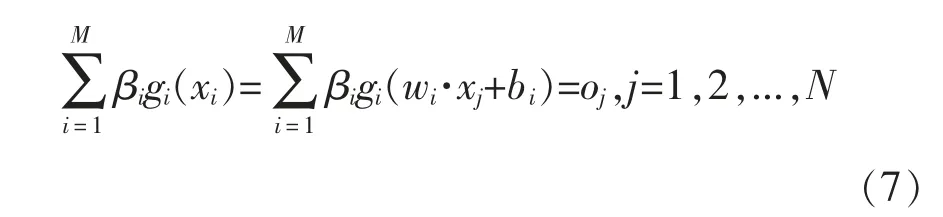
式中：wi是输入层结点和隐藏层结点i 之间的权值向量，βi是隐藏层结点i 和输出层结点之间的权值向量，bi是隐藏层结点i 的偏置值。

当ELM 网络完美拟合所有样本时，该等式可变为：

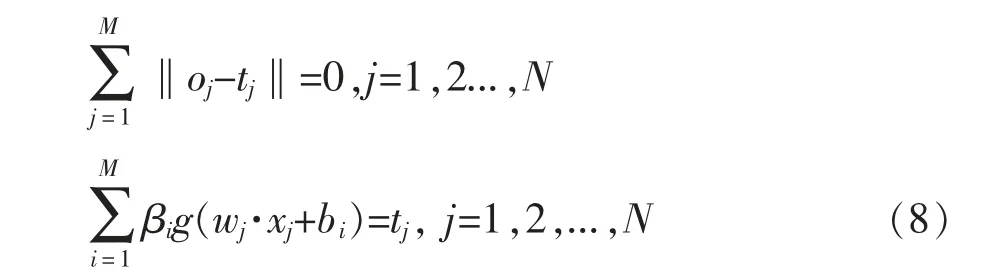
此时等式可以变形为：

式中：H 是ELM 网络隐藏层的输出矩阵，矩阵中的第i 列表示第i 个输入样本对应的输出。并且当前馈神经网络的激活函数是非零连续可微时，网络可以拟合任意的连续函数，故ELM 网络的输入权值向量和偏置值可以随机初始化，在网络训练过程中不再需要迭代更新。

ELM 网络的训练过程如下所示。

第一步：初始化网络中输入层结点和隐藏层结点之间的权值向量w，隐藏层结点的偏置值b；

第二步：计算出隐藏层的输出矩阵H；

第三步：计算出隐藏层结点和输出层结点之间的权值向量β。

4 GSA-ELM 模型

基于GSA 算法优化ELM 网络模型的基本原理是利用引力搜索算法去优化ELM 网络的初始输入权值向量和偏置值。由于原始的ELM 网络的拟合性较强，故ELM 网络的输入权值向量和偏置值可以随机初始化，在网络训练过程中不进行迭代更新。虽然减少了网络的训练时间，但每次产生的初始权值向量和偏置值都是随机的，具有盲目性。本次实验先通过引力搜索算法进行适应度函数寻优，求解最优的初始权值向量和偏置值。适应度函数是训练集的最终输出向量和理论输出向量之间的均方误差（Mean Squared Error），函数表达式如下：

当MSE 的值越小时，表示模型对输入实验数据的预测准确率越高。基于GSA 算法优化ELM 网络模型的具体执行步骤如下。

第一步：处理训练集和测试集样本，确定输入层、隐藏层和输出层的结点个数等参数；

第二步：初始化网络中输入层结点和隐藏层结点之间的权值向量w，隐藏层结点的偏置值b；

第三步：将训练集输入ELM 网络，并通过GSA算法不断调整求解出最优的输入权值向量和偏置值参数；

第四步：将测试集输入GSA 算法训练好的ELM网络中，计算出隐藏层的输出矩阵H、隐藏层结点和输出层结点之间的权值向量β；

第五步：计算出GSA-ELM 网络输出层的预测值并输出。

5 实验结果及分析

5.1 数据集介绍

本次实验所采用的股票预测数据集是来源于真实股票市场的数据，时间从1990 年12 月—2015年12 月，共5 917 条股票数据，每条股票数据包括6 种属性，见表1。

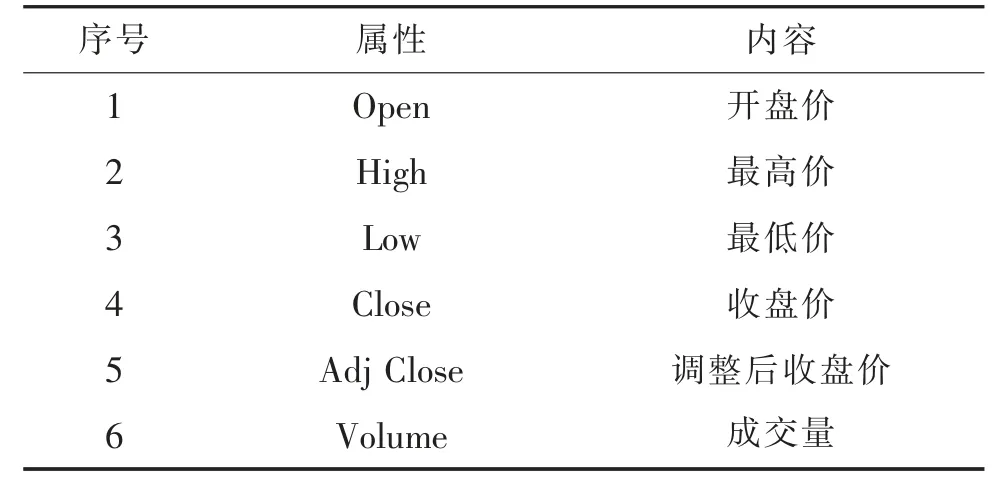
表1 股票数据集的属性值

开盘价是指每个交易日开市后的第一笔每股买卖成交价格；最高价指的是当日所有买卖成交价格中的最大值；最低价指的是当日所有买卖成交价格中的最小值；收盘价是指当日最后一笔交易前1min所有交易的成交量加权平均价格；调整后收盘价指的是在第二天开盘前任何时间发生的任何分配和公司行为导致股票价格发生变化后的最终价格；成交量指的是该交易日内买卖双方所达成交易的总体数量。

本次实验将5 917 条股票数据作为输入样本，通过前一天的6 种股票属性，去预测当天的股票开盘价，故总共产生除最后一天的5 916 条股票市场数据作为输入样本，除第一天的5 916 条股票市场开盘价作为理论输出值。为了更好地展示模型的回归预测能力，选择后100 条股票数据作为测试集，将股票训练数据集输入基于GSA 算法优化ELM 网络的模型中进行训练，最后将测试集输入训练好的模型中进行预测，得出实验结果。

5.2 结果分析

本次实验将GSA 算法优化ELM 网络的模型应用于股票市场价格的预测领域中，利用GSA 算法求解最优解的能力，找出ELM 网络中最优的输入权值向量和偏置值，能够减小回归预测的误差值，提高对股票市场价格的预测准确率。

回归预测的评价指标主要有均方误差（Mean Squared Error，MSE），平均绝对误差（Mean Absolute Error，MAE）和平均百分比误差（Mean Absolute Percent Error，MAPE）等，指标主要的计算方式见表2。

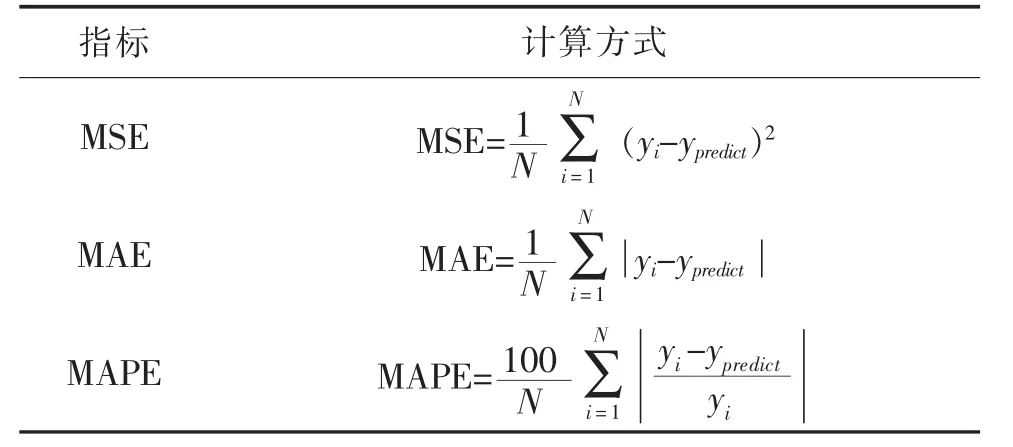
表2 回归预测的评价指标

为了更清晰地表明GSA 算法的优化性能，将基于GSA 算法优化ELM 网络模型和原始的ELM 网络模型进行实验对比分析，将股票测试数据集输入两种模型中进行预测，得出的结果见表3。

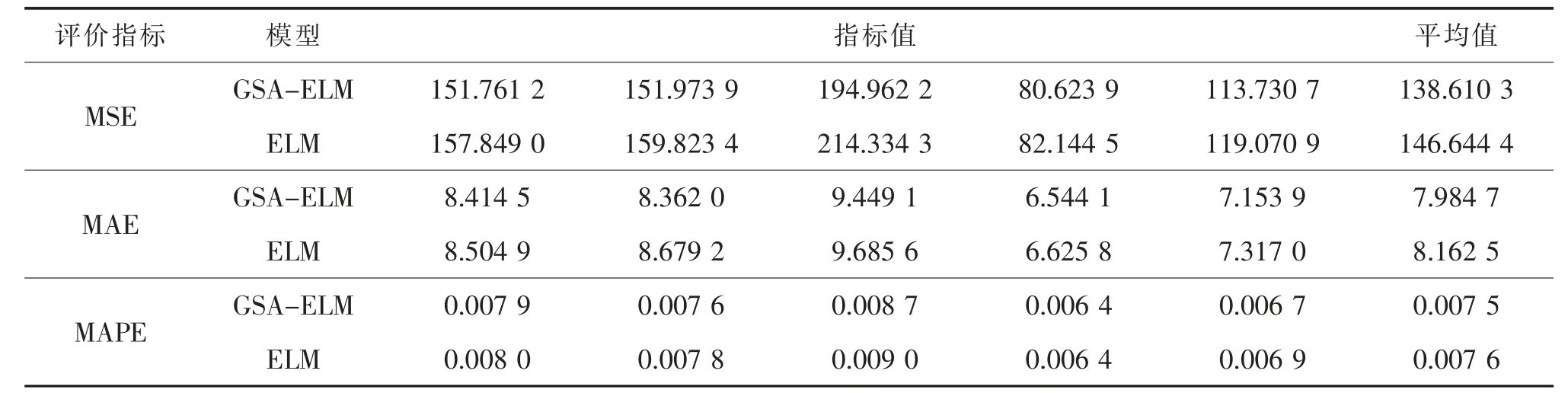
表3 评价指标的实验结果

通过表3 和图2、图3 的实验结果可以得出，在5 次回归预测实验中，GSA-ELM 模型每一次的MSE 值都比ELM 模型要小，MSE 表示模型预测输出值和理论输出值差的平方的期望值，MSE 的值越小，表示GSA-ELM 模型对股票市场数据的回归预测准确率更高；MAE 是绝对误差的平均值，能够更好地评价预测值和理论值误差的实际情况，在5 次实验结果中，GSA-ELM 模型的MAE 值更小，同样表示本研究所提出的模型更优；MAPE 表示预测结果相比理论输出结果的偏离程度，5 次实验结果都表明，GSA-ELM 模型输出值的偏离程度比ELM 模型的偏离程度更小，更加接近于股票测试集数据的输出值。5 次实验结果的平均值也表明GSA-ELM 模型的性能更优，验证了GSA 的优化能力和稳定性，同时对股票市场数据的回归预测准确率更高。

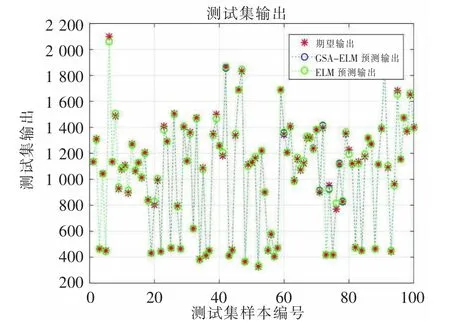
图2 GSA-ELM 和ELM 模型预测图

图3 GSA-ELM 和ELM 模型误差图

6 结论

本研究提出了一种利用引力搜索算法优化极限学习机网络的回归预测模型，并将模型应用于预测股票市场的价格。原始的极限学习机网络由于网络的输入权值向量和偏置值可以随机初始化，在网络训练过程中不再需要迭代更新，但随机初始化的参数具有盲目性，故利用引力搜索算法进行优化，寻找极限学习机网络最优的输入权值向量和偏置值参数，提高了网络的回归预测性能。实验将引力搜索算法优化极限学习机网络模型和原始极限学习机网络模型进行对比实验，计算出回归预测相关的衡量指标，结果表明基于引力搜索算法优化极限学习机网络的回归预测模型在股票市场价格预测中误差更小，有更高的预测准确率。