基于扰动观测器的飞行器轨迹跟踪控制器设计

李传旭, 孟秀云,*, 王 捷

(1. 北京理工大学宇航学院, 北京 100081; 2. 北京电子工程总体研究所, 北京 100854)

0 引 言

随着飞行器作战任务的日益多样化和复杂化,为提升飞行器的飞行性能,往往需要飞行器按照预设的优化轨迹进行飞行,比如固定翼飞行器的栖落机动[1-3]、高超声速飞行器的再入轨迹跟踪[4-5]等。然而飞行器在飞行过程中会受到多种扰动因素的影响,导致实际的飞行轨迹偏离参考轨迹,因此需要设计轨迹跟踪控制器确保飞行器在扰动作用下仍能精确跟踪参考轨迹。一般情况下,参考轨迹是随时间变化的位置信息,轨迹跟踪控制的目的是使飞行器能够在相应时间精确运动到对应位置上[6]。

现有的飞行器轨迹跟踪控制方法从设计思路上可大体分为两类。第一类方法是通过在参考轨迹上设置移动的虚拟目标点,将轨迹跟踪问题转换为制导问题,通过设计制导律控制飞行器追踪目标点,间接实现对参考轨迹的跟踪。文献[7-8]使用速度追踪法跟踪虚拟目标点,并设计了无人机的多回路控制结构。文献[9]在视线角法的基础上引入了一种修正的非线性扰动观测器(modified nonlinear disturbance observer,MNDO),提升了无人飞艇跟踪轨迹时的抗干扰能力。文献[10]使用弹道成型的方法,采用带有攻击角约束弹道成型制导律进行跟踪,降低了跟踪过程的需用过载。文献[11-12]提出了一种非线性制导律,具有较好的曲线跟踪能力,文献[3]将该方法应用于飞行器栖落轨迹的跟踪。文献[13]提出了一种基于虚拟力的制导律,使无人机在跟踪轨迹的同时进行障碍规避。文献[14]设计了一种基于终端滑模和动态面控制的轨迹跟踪制导律,具有较好的鲁棒性。这一类方法能够较好地控制飞行器沿着参考轨迹对应的曲线飞行,但受虚拟目标点选取方式的影响,难以充分利用参考轨迹中的时间信息,较难保证飞行器在相应时间到达对应位置。第二类方法是基于飞行器当前时刻的位置误差设计控制律直接进行轨迹跟踪控制,由于实时的位置误差包含了时间信息,这类方法可以实现位置和时间的精确跟踪。目前已有不少学者基于多种控制理论设计了轨迹跟踪控制器,如比例积分微分控制[2,15]、线性二次型调节控制[5,16]、模型预测控制[17-21]、变结构控制[4,22-25]等。文献[19]基于多级模型预测控制方法实现了旋翼无人机的轨迹跟踪。文献[21]使用无偏模型预测技术,提升了涵道风扇无人机轨迹跟踪控制的鲁棒性。滑模变结构控制(sliding mode control,SMC)在系统模型存在不确定性和外界扰动等因素具有较好的鲁棒性,且对非线性系统有较好的控制效果,因此被广泛应用于轨迹跟踪控制。文献[4]设计了自适应滑模控制器用于高超声速飞行器的纵向轨迹跟踪。文献[22]使用模糊逻辑系统近似的滑模控制方法实现了平流层卫星的轨迹跟踪。文献[24]基于自适应终端滑模控制理论设计了水下航行器的深度跟踪控制器。文献[25]运用自适应反步滑模方法设计了欠驱动飞艇的轨迹跟踪控制器,具有良好的抗干扰能力。

现有的飞行器轨迹跟踪控制方法主要研究的是二维平面内轨迹跟踪问题,而对三维轨迹跟踪问题的研究相对较少。三维轨迹跟踪控制器的设计需要考虑飞行器产生机动力方式,固定翼飞行器主要采用倾斜转弯(bank-to-turn,BTT)的控制方式,通过滚转运动改变升力面的方向从而产生侧向过载,实现转弯机动。对于滑模控制方法,终端滑模(terminal sliding mode, TSM)相较传统线性滑模面具有有限时间收敛的优点,非奇异TSM(nonsingular TSM, NTSM)控制解决了TSM存在的控制指令奇异问题。为进一步解决NTSM在系统远离平衡点时收敛较慢的问题,文献[26-27]提出了非奇异快速终端滑模控制(nonsingular fast TSM, NFTSM)方法,对于提升轨迹跟踪控制器性能具有较大应用价值。

本文针对多种扰动作用下的固定翼飞行器三维轨迹跟踪问题,首先建立BTT控制方式下的飞行器三维轨迹跟踪误差模型,为增强轨迹跟踪控制器的抗干扰能力,在非线性扰动观测器的基础上引入状态估计误差反馈,提升对时变扰动的估计能力。为进一步提升轨迹跟踪控制器的快速性,基于NFTSM方法,采用双幂次趋近律设计三维轨迹跟踪控制器。最后,结合实际工程应用对本文设计的轨迹跟踪控制器进行仿真分析。

1 问题描述与模型建立

对于BTT控制方式的飞行器,在理想情况下其侧滑角为零,滚转角近似等于速度倾斜角,并考虑到在常规飞行条件下发动机推力主要影响飞行速度的大小,对速度方向的影响较小,因此在建模时将推力的影响作近似处理,将建模误差视为扰动项。基于上述条件,得到BTT飞行器三维质心运动方程组为

(1)

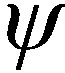
(2)

式中:CD为阻力系数;Sref为参考面积;ρ为大气密度。

已知参考轨迹xd(t)、yd(t)、zd(t)为随时间变化的三维空间位置,轨迹跟踪的目标是控制飞行器的质心在相应时间精确运动到对应的位置。下面建立BTT飞行器三维轨迹跟踪误差模型。定义当前时刻飞行器x、y、z3个方向的轨迹跟踪误差分别为

(3)

为表明控制输入与轨迹跟踪误差的关系,对其沿时间求二阶导数,将式(1)代入,得到轨迹跟踪误差模型为

(4)

式中:L为旋转矩阵,其表达式为

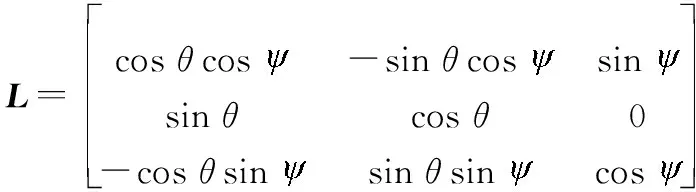
(5)

2 扰动观测器设计

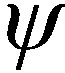
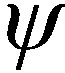
2.1 非线性扰动观测器

对于一般一阶非线性系统：

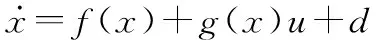
(6)

式中:x为系统的状态变量;f(x)和g(x)为已知非线性函数;u为控制量;d为未知扰动项。NDO的一般形式如下[28]:

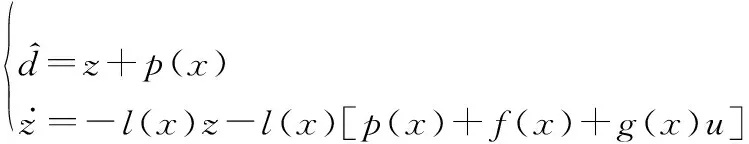
(7)

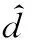
(8)

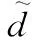
(9)

2.2 基于状态估计误差反馈的扰动观测器设计

为提高NDO对时变扰动的估计能力,在NDO的基础上引入状态估计误差反馈,设计改进的NDO(improved NDO, INDO)。

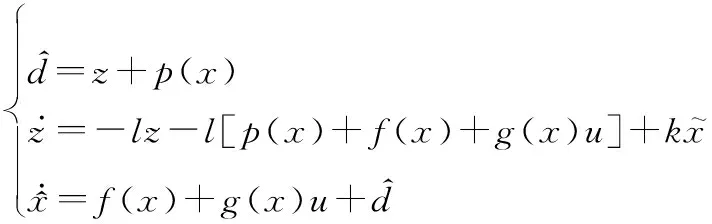
(10)

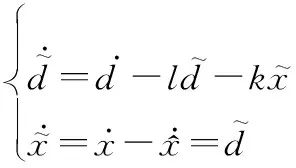
(11)

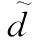
(12)

(13)

为保证扰动观测器稳定,系统的特征根应具有负实部,所以扰动观测器的设计参数应满足l>0且k>0。相较于传统NDO,INDO可以无静差地跟踪斜坡输入,具有更好的估计时变扰动的能力。

3 三维轨迹跟踪控制器设计

3.1 基于双幂次趋近律的NFTSM控制方法

考虑如下含未知扰动的二阶非线性单输入单输出(single input single output,SISO)系统:

(14)

式中:x=[x1,x2]T为系统状态量;u为控制输入;d为未知扰动;y为系统输出;f(x,t)和g(x,t)为已知函数。

为使系统状态在有限时间收敛,并在避免控制量奇异的同时提升系统远离平衡点时的收敛速度,选取NFTSM滑模面[27]为

(15)

式中：设计参数m,n,p,q均为正奇数,并且满足1

p/q;α,β∈R+。对于被控对象(14),当系统处于滑动模态时,系统状态能够在有限时间收敛。

为保证系统能够在有限时间到达滑动平面,并进一步提升收敛速度,同时避免系统抖振,采用双幂次趋近律[29]。由于选取的是NFTSM滑模面,为避免控制律中出现负指数项导致控制律奇异,对双幂次趋近律进行调整,得到如下趋近律:

(16)

其中,设计参数k1>0,k2>0,γ1>1,0<γ2<1。

对滑模函数s求导可得

(17)

(18)

控制律中的k1|s|γ1sgns项和k2|s|γ2sgns项均为连续函数,因此能够避免由非连续切换项导致的抖振问题。

3.2 稳定性分析

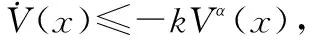
(19)

式中:V(x0)为V(x)的初值。

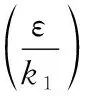
(20)

证明构造Lyapunov函数

V=0.5s2

对其沿时间求导可得

(21)

将控制律(18)代入式(21),可得

(22)

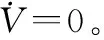
(23)

(24)

经变形可得

(25)

(26)

已知0<γ2<1,则0.5<(γ2+1)/2<1,根据引理1可知,系统能在有限时间内收敛到区域

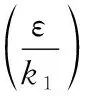
(27)

证毕

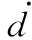
3.3 INDO-NFTSM三维轨迹跟踪控制器设计

飞行器在三维空间中的质心运动本质上为质点的三维运动问题。对于三维空间中的质点,若其控制输入为惯性坐标系三轴的加速度,则它在惯性坐标系中3个方向的运动是相互独立的。

由于飞行器的轨迹跟踪误差是在惯性坐标系中描述的,为了将轨迹跟踪控制器从x、y、z3个方向分开进行设计,给出惯性坐标系三轴加速度与BTT控制方式下飞行器的控制量推力P、法向加速度ay、滚转角γ的转换关系。定义3个中间控制量ux、uy、uz,并定义dx、dy、dz3个中间扰动项,表达式为

(28)

中间控制量ux、uy、uz的实际物理含义为飞行器加速度在惯性坐标系3个方向的分量。由此可将式(4)改写为

(29)

若将中间控制量视为控制输入,将跟踪误差视为输出,则可将三维轨迹跟踪误差模型按x、y、z方向分解为3个相互独立的如式(14)的二阶SISO子系统。

根据式(15),对于分解后的3个子系统分别选取NFTSM滑模面,各方向的参数用下标x、y、z加以区分,滑模面形式为

(30)

(31)

最后根据式(28)对中间控制量进行变换,得到BTT飞行器三维轨迹跟踪控制律为

(32)

其中,T1、T2、T3为中间量,表达式为

(33)

4 仿真结果与分析

本文采用的固定翼飞行器基本参数为:M=300 kg,Sref=0.06 m2,CD=0.5。考虑实际飞行条件限制,采用BTT-45控制方式,限制滚转角指令γcmd范围在±45°范围内,限制可用推力范围为300～1 500 N;可用法向加速度范围为±40 m/s2。考虑到飞行器姿态回路和发动机的工作特性,仿真时将飞行器对推力指令、法向加速度指令和滚转角指令的响应过程等效为二阶振荡环节:推力控制回路的自然频率为15 rad/s,阻尼比为0.9;法向过载控制回路的自然频率为25 rad/s,阻尼比为0.8;滚转角控制回路的自然频率为30 rad/s,阻尼比为0.8。

在INDO-NFTSM三维轨迹跟踪控制器中:滑模面参数选取为:αx=6,βx=0.8,αy=5,βy=1,αz=6,βz=0.8,mx=my=mz=7,nx=ny=nz=3,px=py=pz=5,qx=qy=qz=3;趋近律参数选取为:k1x=0.1,k2x=0.8,k1y=0.2,k2y=1.2,k1z=0.1,k2z=0.8,γ1x=γ1y=γ1z=1.5,γ2x=γ2y=γ2z=0.5。

选取文献[28]提出的NDO与文献[9]提出的MNDO进行对比仿真分析。为确保3种扰动观测器具有相近的响应速度,选取NDO的参数为lNDO=17.5,MNDO的参数为lMNDO=12.5,kMNDO=19.5,INDO的参数为lINDO=32,kINDO=400。

4.1 匀速直线轨迹跟踪

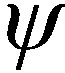
参考匀速直线轨迹保持1 000 m的飞行高度,飞行速度大小为200 m/s,速度方向朝x正方向。

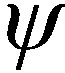
仿真结果如图1和图2所示。

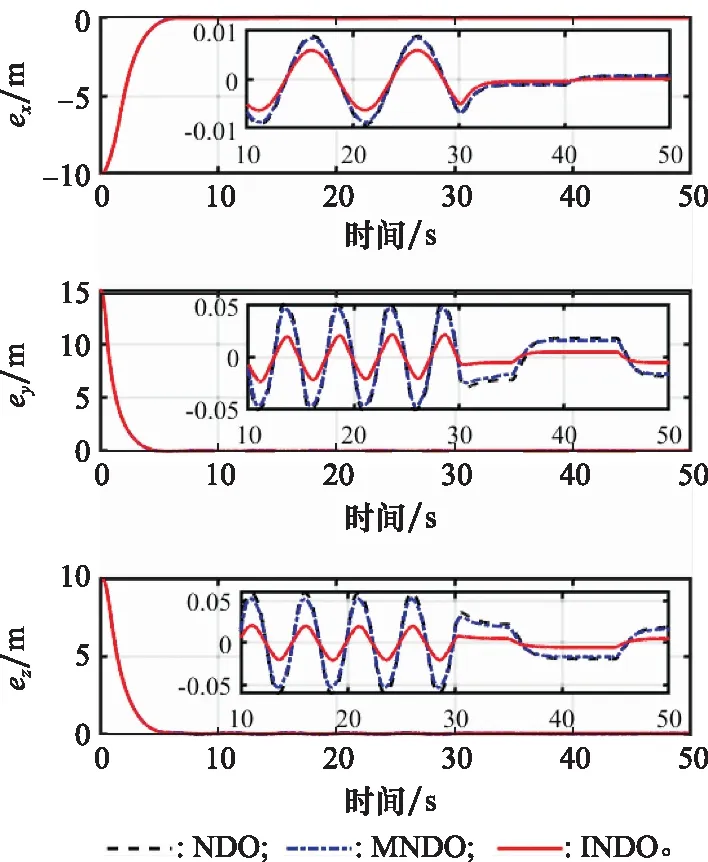
图1 匀速直线轨迹跟踪误差曲线Fig.1 Tracking error curve of uniform linear trajectory

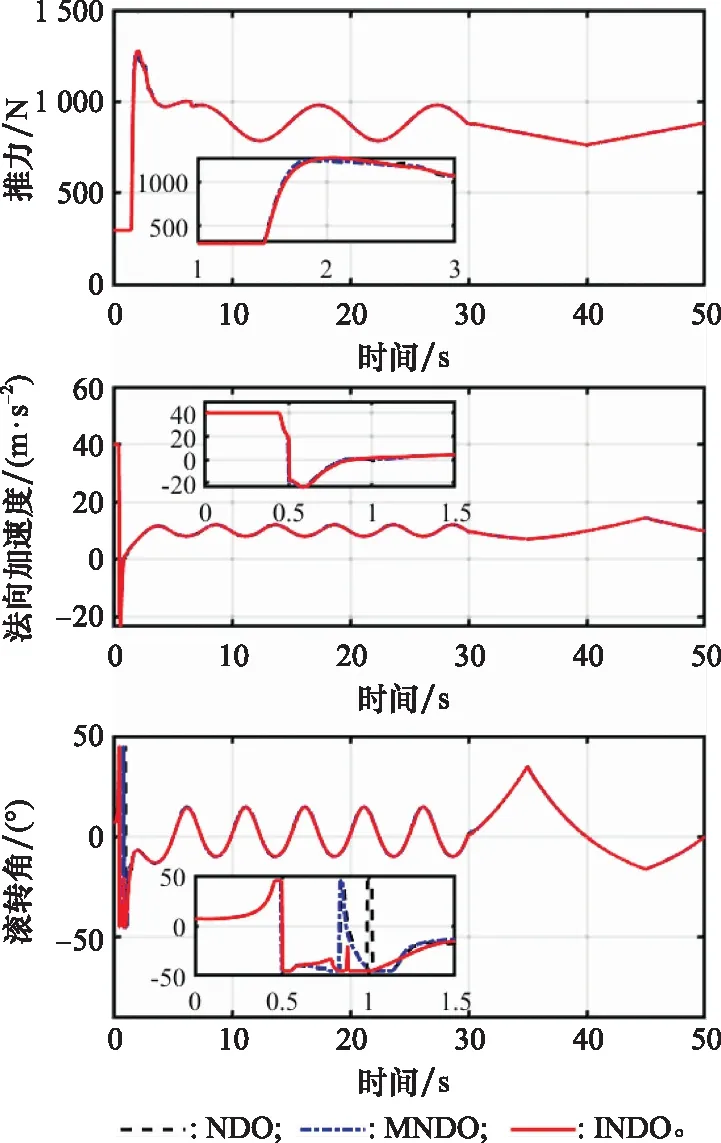
图2 匀速直线轨迹跟踪控制量变化曲线Fig.2 Control input curve of uniform linear trajectory

从图1中可以看出,在多种扰动的综合作用下,INDO-NFTSM三维轨迹跟踪控制器能较好地控制飞行器跟踪匀速直线参考轨迹,x、y、z3个方向的跟踪误差均能够快速收敛至0附近,且超调量较小,x方向最大跟踪误差为0.006 m,y、z方向最大跟踪误差为0.02 m,系统具有较高的跟踪精度和良好的鲁棒性。采用MNDO的跟踪精度略微高于NDO,两者在x方向的最大跟踪误差均在0.01 m附近,y、z方向最大跟踪误差均在0.05 m附近。说明在时变扰动作用下,采用INDO的跟踪精度明显高于NDO和MNDO,且过渡过程平缓。

从图2中可以看出,轨迹跟踪控制器能够控制飞行器持续机动以减弱外界扰动的影响。同时可以发现由于采用了双幂次趋近律,推力、法向加速度、滚转角3个控制指令均没有出现明显的抖振现象。

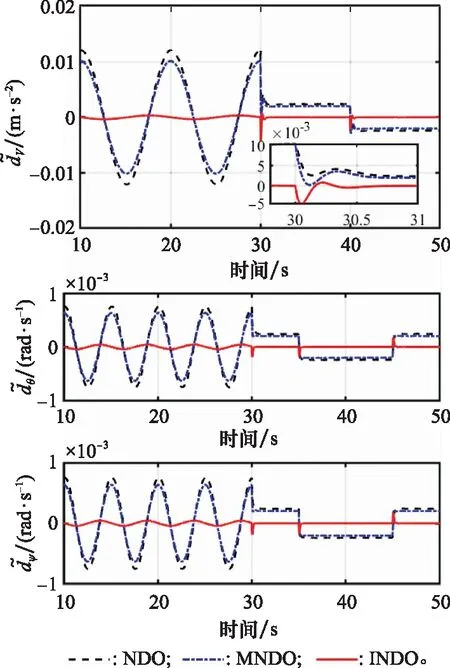
图3 扰动估计误差曲线Fig.3 Disturbance estimation error curve

4.2 空间机动轨迹跟踪

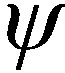
参考轨迹的初始高度为1 000 m,初始速度为150 m/s,速度方向朝x正方向,加速度为1 m/s2,爬升速度倾角为5°,侧向蛇形机动周期为25 s,最大需用滚转角为35°。

仿真结果如图4～图7所示。

图4 空间机动飞行轨迹Fig.4 Maneuvering flight trajectory

图5 空间机动轨迹跟踪误差曲线Fig.5 Tracking error curve of maneuvering trajectory

从图4和图5中可以看出,在同时存在初始位置偏差和航向偏差的情况下,飞行器能够快速修正误差进行蛇形机动爬升,跟踪误差能够收敛至0附近。采用NDO时,x方向最大跟踪误差为0.04 m,y方向为0.022 m,z方向为0.14 m;采用MNDO时,x方向最大跟踪误差为0.02 m,y方向为0.02 m,z方向为0.07 m;采用INDO时,x方向最大跟踪误差为0.013 m,y方向为0.017 m,z方向为0.04 m。在图7中,由于初始状态落后于参考轨迹,飞行器需要先额外加速进行追踪,在跟踪上参考轨迹后,飞行器能够保持1 m/s2的加速度进行匀加速飞行,与参考轨迹要求相同。

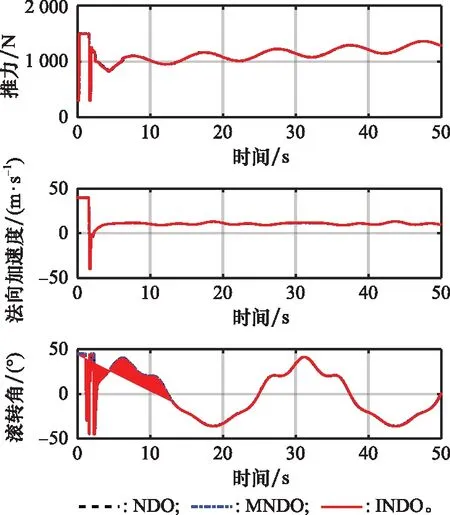
图6 空间机动轨迹跟踪控制量变化曲线Fig.6 Control input curve of maneuvering trajectory

图7 飞行速度大小变化曲线Fig.7 Flight velocity curve

采用INDO时飞行器的轨迹跟踪误差明显小于NDO和MNDO。说明在扰动作用下,INDO-NFTSM三维轨迹跟踪控制器对于空间机动轨迹仍具有良好的跟踪能力。

5 结 论

本文针对多种扰动影响下的固定翼飞行器三维轨迹跟踪问题,设计了一种基于改进非线性扰动观测器的非奇异快速终端滑模三维轨迹跟踪控制器。首先推导了BTT控制下的飞行器三维轨迹跟踪误差模型,然后设计了基于状态估计误差反馈的INDO观测器对系统的综合扰动进行观测。之后基于NFTSM控制方法,使用双幂次趋近律设计了三维轨迹跟踪控制器,并证明了闭环控制系统的稳定性。最后分别使用匀速直线轨迹和蛇形爬升机动轨迹检验本文设计的轨迹跟踪控制器性能。仿真结果表明,本文设计的INDO观测器能够较好地观测时变扰动,在系统模型不确定性和外界扰动的综合作用下,所设计的轨迹跟踪控制器能够对三维轨迹进行准确、稳定的跟踪。