基于Agent的体系过程A-GERT网络“刺激-反应”学习模型

方志耕, 夏悦馨,*, 张靖如, 熊 仪, 陈静邑

(1. 南京航空航天大学经济与管理学院, 江苏 南京 211100;2. 南京航空航天大学灰色系统研究所, 江苏 南京 211100)

0 引 言

图示评审技术(graphic evaluation and review technique, GERT)[1]是由Elmaghraby和Pritsker提出的一种概率型随机网络,近年来,GERT在项目进度规划[2]、灾害应急预警[3]、供应链优化流程[4]、卫星网络[5]等领域得到广泛的应用。GERT网络可以通过概率分支决定下一节点的状态,网络节点具有决策功能,能够很好地研究具有决策过程的现实问题。陈东平等[6]将GERT网络应用于工程计划管理中,通过模拟解模型过程的分析从而寻找GERT网络解,决策出关键线路。杨保华等[7]基于GERT网络构建突发事件情景推演耦合模型,为“情景-应对”决策研究提供了新思路。郭本海等[8-10]通过对GERT网络模型节点决策概率的研究,分析了产业价值流动、资源优化配置等问题。张海涛等[11]构建了网络信息价值流动的GERT网络模型,通过分析网络模型的传递参数描述信息生态链中各信息主体之间的价值流动过程。通过以上研究不难看出,GERT网络在解决网络流程分析、逻辑决策等方面发挥了重要的作用。但GERT网络在应用决策过程中通常都设定节点传递概率是静态不变的,而在实际决策过程中,传递概率的大小很大程度上决定了链路的优劣,在不确定环境以及不同系统目标的影响下,网络传递概率会发生动态变化,决策结果也会相应改变。

另一方面,随着人工智能技术的不断发展,基于智能体(Agent)的学习决策[12-14]已成为决策问题研究的热点之一。关于Agent的定义,Wooldrige等[15]认为Agent不仅具有自适应性、社会性、反应性和能动性,还具备一些人类才有的信念、意图等性质。基于Agent的决策系统具有很好的学习能动性和环境自适应性,因此将Agent应用于GERT网络中研究决策问题可以形成良好的互补关系。研究Agent的GERT网络决策问题主要包含两个方面:一是决策节点能够无阻碍有效识别路径,即减少回路的概率流动,最大程度地规划有效路径；二是根据不同的目标要求,实现最优路径的概率最大化。目前虽然已有蒋子涵等[16]将GERT网络和Agent技术结合起来,但主要关注的是Agent学习算法的一致性分析,较少从GERT网络模型的角度研究路径概率学习决策问题。

以上两个决策问题本质上即是决策节点的反馈学习问题,在研究Agent的学习问题中,迭代学习的概念[17]自Uchiyama首次提出后便引起了广泛关注,由于迭代学习具有能够从以前迭代的经验中进行学习的优点,可以有效地实现对Agent系统的精确跟踪。在早期的迭代学习研究[18-19]中,学习算法通过增加固定的效益来进行迭代,但削弱了不确定性所带来的影响。之后,Chi等[20]和Lin等[21]引入了自适应控制的思想,提出了一种自适应迭代学习方法。Chen等[22-23]针对非线性系统提出了模糊自适应迭代学习方法。但在自适应迭代学习过程分析中仍需要一些先验模型信息,如线性参数和系统状态等。而随着系统网络结构的复杂化,模型过强的非线性也导致学习分析十分困难。针对迭代学习存在的自适应性以及非线性问题,约翰霍兰教授提出的复杂适应系统(complex adaptive system, CAS)[24]理论中最为核心的概念就是适应性主体,简称主体。主体与外部环境之间能动的不断学习的交互作用所体现的就是适应性。刺激-反应模型[25-27]作为CAS理论中的基本模型在自适应学习以及决策领域得到了广泛应用,主体通过外界刺激反馈驱动系统做出反应,仅利用输入输出实现对复杂系统的迭代学习,对于研究非线性系统有较强的适应性。

综上所述,就GERT网络决策以及Agent学习研究而言,存在的局限性主要有以下3个方面:① 多数GERT网络研究主要针对活动过程的描述分析,传递概率通常都是静态不变的,未考虑网络节点本身因环境影响所带来的传递概率的变化,决策节点不具备学习能动性。② 在Agent技术与GERT网络结合的研究中,大多针对学习算法本身的分析研究,很少从网络决策节点的角度去探讨概率的路径优化学习。③ 在Agent迭代学习方面,系统的环境自适应性与模型过强的非线性问题导致迭代学习十分困难。

因此,本文针对以上局限性,首先将Agent技术与GERT网络节点结合起来,形成智能决策节点;然后在A-GERT网络的基础上结合刺激-反应模型,通过网络节点的传递效用值进一步拓展刺激-反应模型,建立迭代学习反馈机制,并运用动态规划原理依次对网络节点进行概率学习;最后给出了基于Agent的A-GERT网络“刺激-反应”模型的设计步骤,并以创新技术开发活动资源配置决策问题为例,验证本模型的有效性和合理性。

1 基于Agent的体系过程GERT网络逻辑及其结构设计

系统是由相互关联的要素构成的整体。而体系则是由系统所构成的一个协同(联盟)整体,因为体系中的系统可能具有较强的独立性,甚至有时,某(几个)系统可以部分(完全)地代表它的总体。因此,体系与系统的一个重要区别在于,体系一般都具有一定的可靠性结构和量值韧性,而系统一般却很难具有这样的性质。

定义 1体系过程Ψ(t):若某体系是一种由若干系统Si(i=1,2,…,n)组成,且协同完成某种(些)任务的随机(网络)过程,则称其为体系任务网络随机过程,简称随机过程,用Ψ(t)表示。

定义 2自学习体系过程ΨAgent(t):在Ψ(t)过程中,若把某个(些)系统(组织)看作Agent,具有向过程或历史学习的机制和能力,则称该体系为具有Agent自学习机制的过程,其本质是一种由若干智能代理人Agent构成的协作过程,用ΨAgent(t)表示。

定义 3体系自学习网络ΨAgent(N(t),S(t)):若将ΨAgent(t)过程用广义活动网络(generalized active network, GAN)[28]的逻辑机制进行表征,则称所得到的网络为具有Agent自学习机制的体系过程网络,用ΨAgent(N(t),S(t))表示,其中:N(t)和S(t)分别表示某系统具有自学习机制的网络节点和边。

根据随机网络原理,对于任一客观体系过程,可以看作是基于任务目标的各系统之间相互协作过程,一般情况下,这种任务的协作过程可以运用GAN进行表征,逻辑节点构成见图1。这里值得注意的是,N(t)和S(t)分别表示各系统(组织)经过学习,其状态和过程可能都会逐步改善或得到完善,其(t)表示是一个时间的映射。为了便于区别,在其逻辑节点上加注点(见图1、图2)。

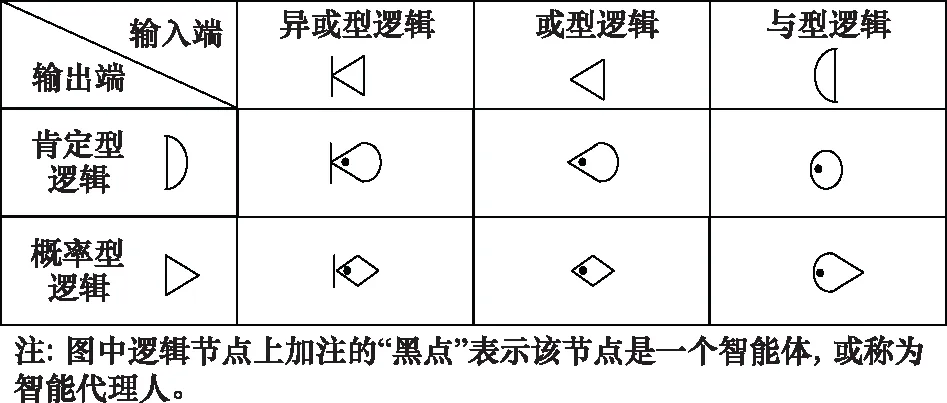
图1 GAN网络节点类型Fig.1 Type of GAN network node

图2 ΨAgent(N(t),S(t))网络的要素Fig.2 Elements of ΨAgent(N(t),S(t)) networks

定义 4ΨAgent(N(t),S(t))网络:在ΨAgent(N(t),S(t))网络中,若依据逻辑转换规则,将其所有节点都转换成异或型,则称该网络为具有自学习机制的A-GERT,为简便,该网络用ΨA-GERT(N(t),S(t))表示。

例 1某体系中,节点i保持其在原状态的概率为pii,到后续节点jk(k=1,2,…,K)的概率分别为pij1,pij2,…,pijK,试画出该节点与其后续节点的ΨA-GERT(N(t),S(t))图。

利用上述各定义中的A-GERT网络逻辑画出其ΨA-GERT(N(t),S(t))网络图,如图3所示。

图3 某体系节点i到jk(k=1,2,…,K)的ΨA-GERT(N(t),S(t)) 网络示意图Fig.3 Schematic diagram of the ΨA-GERT(N(t),S(t)) network of system nodes i to jk(k=1,2,…,K)

A-GERT网络与常规的GERT网络的区别主要体现在决策节点的学习能动性,节点在外界环境刺激下可以动态地调整传递概率,从而改善体系活动过程。

定义 5[28]ΨA-GERT(N(t),S(t))网络的解析算法:假设随机变量tijK为活动ijK的完成时间,要知道活动ijK的执行情况,就要知道活动ijK被执行的概率以及tijK的概率分布或概率密度函数。

令f(tijK)为活动ijK的条件概率密度函数,P(tijK)为活动ijK的条件概率分布函数,则随机变量的矩母函数为

(1)

定义WijK(s)为活动ijK的传递函数,则WijK(s)=pjk·Mijk(s)。如图4所示,ΨA-GERT(N(t),S(t))网络主要包含串联结构、并联结构以及自环结构。

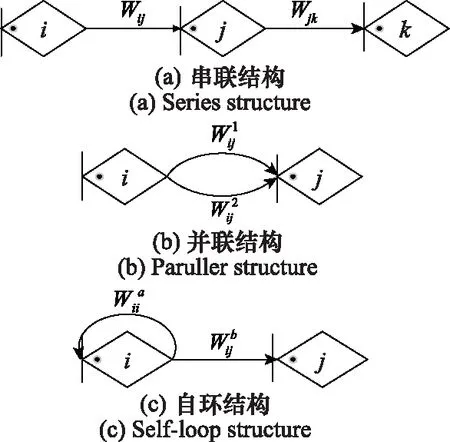
图4 ΨA-GERT(N(t),S(t))网络串联、并联、自环结构图Fig.4 ΨA-GERT(N(t),S(t)) network in series, parallel and self-loop structure diagram

(1) 对于串联结构,节点i与k之间等效传递函数为

Wik=Wij+Wjk=Mij(s)pij+Mjk(s)pjk

(2)

(2) 对于并联结构,节点i与j之间等效传递函数为

(3)

(3) 对于自环结构,节点i与j之间等效传递函数为

(4)

定理 1设WEijk(s)(k=1,2,…,K)为节点i到节点jk的直达路径的等价传递函数,节点i到节点jk的等价传递概率pEijk等于s=0时的WEijk(s)的值。节点i到节点jk的传递随机变量tijk的期望时间TEijk等于矩母函数MEijk(s)的一阶导数在s=0时的值。

证明两节点的等价传递函数WEijk(s)=MEijk(s)·pEijk,由ΨA-GERT(N(t),S(t))网络矩母函数的特性可知,在s=0时,

(5)

因此,等价传递概率pEijk等于s=0时的WEijk(s)的值。

根据矩母函数的基本性质,即矩母函数的一阶导数在s=0处的数值,就是网络传递的随机变量的一阶原点矩,因此有

(6)

证毕

2 体系过程的“刺激-反应”学习反馈结构及其机制分析

如今随着系统网络结构的日益复杂化,体系过程学习模型的建立和分析也更加困难,系统的自适应学习已成为研究的重点之一。而CAS理论中最为核心的概念就是适应性主体,简称主体。刺激-反应模型[25-27]是CAS理论中的基本模型,模型主体仅利用输入输出实现对复杂系统的迭代学习,具有较强的适应性。因此,本文通过对刺激-反应模型的分析研究,并结合A-GERT网络进一步拓展刺激-反应模型。

定义 6刺激-反应模型[25]:刺激-反应模型主要由一个主体(探测器)、If/Then规则集合和一个主体行为(效应器)组成,系统所处环境刺激主体,主体从刺激信号中抽取信息,信息通过规则集反复处理,寻找最优匹配,根据If/Then规则集合判断,传达到效应器,由效应器做出反应,即主体行为,见图5。

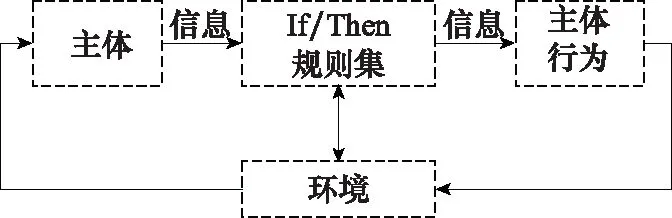
图5 刺激-反应模型Fig.5 Stimulus-response model

定义 7网络节点i的传递效用函数:在ΨA-GERT(N(t),S(t))网络中,决策节点集合N(t)中某节点i在决策行动后,从节点i到jk的活动均经历相应参数,即某条道路(i,jk)选择所导致成功或者失败的节点jk效用值Vjk、路径(i,jk)实现期望概率pEijk、路径(i,jk)所消耗的期望时间TEijk,该节点i行动的传递效用值函数Fi可以定义为

(7)

其中,终节点效用值指标Vjk可直接给出,例如活动经济效益、活动效能等。由式(7)可知,节点i行动的传递效用值函数Fi与TEijk成反比,与pEijk和Vjk成正比。此外,需注意的是在计算Fi时,节点jk不包含回路节点,因为回路节点jk的效用值Vjk可认为是0。

定义 8ΨAF-GERT(N(t),S(t))智能反馈网络:在ΨA-GERT(N(t),S(t))网络中,各决策节点i均能对其决策后果的效用值函数Fi值进行观察、评价,并能利用这一结果效用值Fi来改善其下一步的决策,则称该网络为具有反馈机制的智能网络,记为ΨAF-GERT(N(t),S(t))。

例2试画出某体系节点i到jk的ΨA-GERT(N(t),S(t))的智能反馈网络ΨAF-GERT(N(t),S(t))图。

依据定义7和定义8,设计节点的反馈节点与反馈回路(图中虚线),如图6所示。节点i到达节点jk(k=1,2,…,K)时,均会获得不同程度的效果值Vjk。再通过Agent反馈的Fi值来判断下一步路径(i,jk)的概率值。

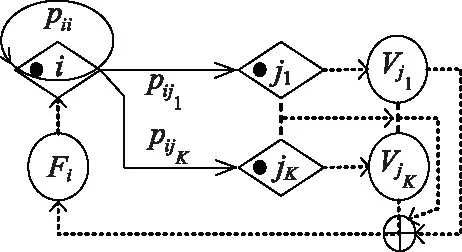
图6 某体系节点i到jk的ΨAF-GERT(N(t),S(t))网络结构示意图Fig.6 Schematic diagram of ΨAF-GERT(N(t),S(t)) network structure from system node i to jk

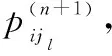
(8)

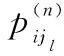
(9)

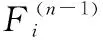
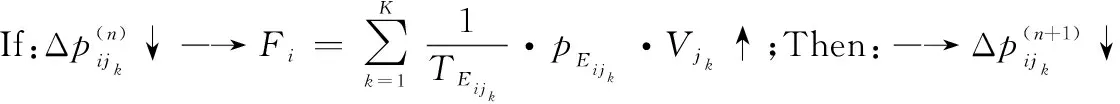
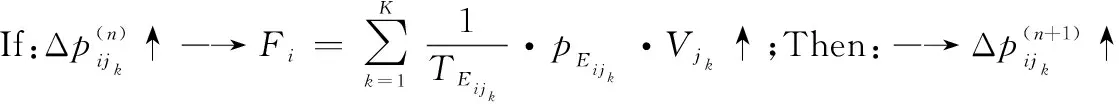
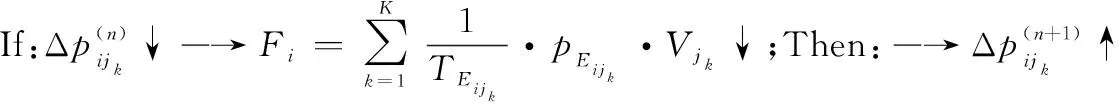
证毕

(10)

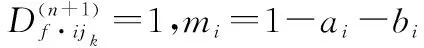
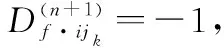
故,式(10)得证。

证毕

(11)

(12)

式中:ξai和ξbi分别为“正”“负”政策激励强度系数调节参数。

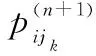
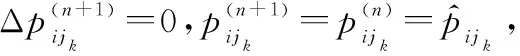
证毕

推论 2节点i中ξai和ξbi的取值:对于节点i,ξai和ξbi取值范围满足0≤ξbi<ξai≤1且0≤ξaiξbi≤1/4。

2014年8月20日，郭恒信又一次来到阿里甫·司马义家中，将2000元的学费递到儿子买买江·阿里甫手中，又一次圆了孩子上学的梦想。

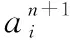
证毕

3 基于A-GERT网络的“刺激-反应”概率学习迭代模型构建

通过对“刺激-反应”模型反馈机制的分析,进一步将AF-GERT网络逐个分解,建立动态的迭代秩序,实现决策节点路径概率学习的最优化。

定理 5“刺激-反应”智能学习决策动态迭代秩序:在ΨAF-GERT(N(t),S(t))网络中,进行“刺激-反应”智能学习决策动态迭代时,保证全网络最优的秩序是,与网络概率传递方向相反,由终节点N向始节点1进行迭代,其秩序为

N→(N-1)→…→i→(i-1)→…→2→1

(13)

由于ΨAF-GERT(N(t),S(t))网络是一种有向动态网络,在该网络中通过“刺激-反应”的智能学习方式进行最优路径发现决策的本质是一个多阶段动态规划问题。运用动态规划的Bellman原理,可构造出该问题的动态迭代秩序(见式13)。

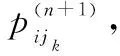
步骤 1建立Agent反馈网络ΨAF-GERT(N(t),S(t))。

依据定义8,把定义4的ΨA-GERT(N(t),S(t))转换成具有效用反馈结构的ΨAF-GERT(N(t),S(t))体系,如图6所示。由于体系网络往往由很多节点和边构成,按照从终节点N向始节点1依次进行迭代的规则,将原始的A-GERT网络分解为多个单一AF-GERT结构,以便后续概率迭代计算。

步骤 2建立网络体系ΨAF-GERT(N(t),S(t))的初始假设与迭代规则。

初始条件与假设:根据已知条件,对网络需要迭代的节点和边进行赋值,主要包括节点活动间的传递概率与传递时间,以及终节点N效用价值的分析设定(例如体系要求评定的经济效益、效能、利润等指标)。

迭代秩序设计:在智能反馈网络体系中,运用推论1进行动态迭代秩序设计,迭代秩序见图7。

图7 迭代程序图Fig.7 Iterative program diagram

步骤 3第i(i∈N(t))个节点的n+1步迭代。

在对第i个节点进行路径概率迭代时,当迭代路径只有两条时,可任选一条进行概率迭代;当迭代路径大于两条时,则任选两条路径进行概率学习,且此时其他路径概率保持原始值不变,直至达到节点路径均衡解时,即停止迭代。

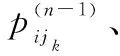
(14)

当体系网络概率学习同时考虑效用值及网络传递时间时,节点i第n步和第n-1步的传递效用值为

(15)

根据式(6)可得:当ijk为最优路径时,

(16)

当ijk为非最优路径时,

(17)

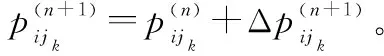
步骤 4第i(i∈N(t))个节点的智能自学习概率配置迭代解。

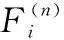
步骤 5ΨAF-GERT(N(t),S(t))的路径智能自学习选择最满意解决方案。

根据图7的“刺激-反应”学习动态迭代程序,在ΨAF-GERT(N(t),S(t))网络体系中,按步骤3和步骤4进行各智能决策节点的逐个迭代,最终会得到该网络路径学习的最满意解决方案。

证毕

4 案例研究

4.1 基于创新技术方案决策问题的A-GERT网络“刺激-反应”学习模型构建与求解

在创新开发资源有限的情况下,根据不同目标动态选择最优的技术开发路径、明确资源流动方向是典型的体系活动决策问题。根据文献[11]以及传统的创新技术开发项目情况,依据定义4,构成的技术开发A-GERT体系网络如图8所示,各节点之间信息流动的传递函数用Wij表示。节点1表示创新技术生成与评价、节点2表示市场调研与需求预测、节点3表示项目方案总体设计、节点4、5分别表示2种新技术A、B的研究,节点6、7分别表示对新技术A、B进行试验，节点8表示技术开发试验成功,节点9表示技术开发试验失败。

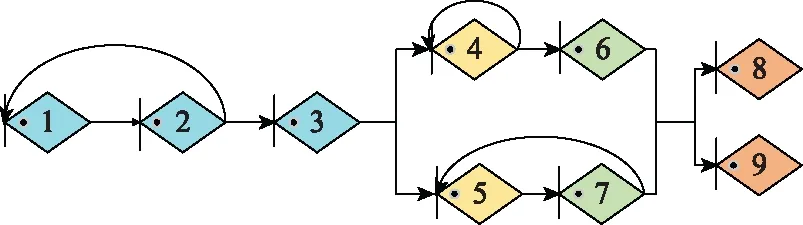
图8 技术开发体系ΨA-GERT(N(t),S(t))网络Fig.8 ΨA-GERT(N(t),S(t)) network of technology development system

步骤 1依据定义8,根据图8构建的技术开发体系过程智能反馈AF-GERT网络,如图9所示。

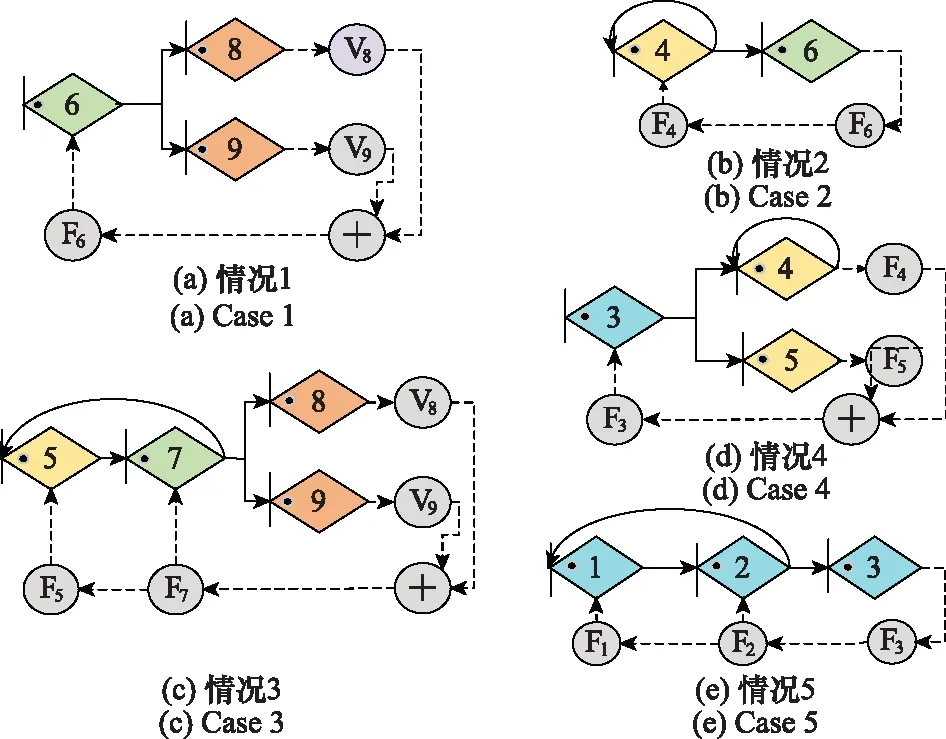
图9 技术开发体系ΨAF-GERT(N(t),S(t))网络Fig.9 ΨAF-GERT(N(t),S(t)) network of technology development system

步骤 2网络体系的初始假设。

各节点间的初始概率与时间如表1所示。已知到达节点8与到达节点9分别可获得的经济效益为V8=200,V9=-100。每个决策节点均实施管控措施,各节点管控措施的正、负刺激因子分别为εa6=0.2,εb6=0.04;εa4=0.3,εb4=0.01;εa7=0.2,εb7=0.01;εa3=0.3,εb3=0.03;εa2=0.3,εb2=0.05。此外,设定网络学习的初始概率增值Δp1为0.01。

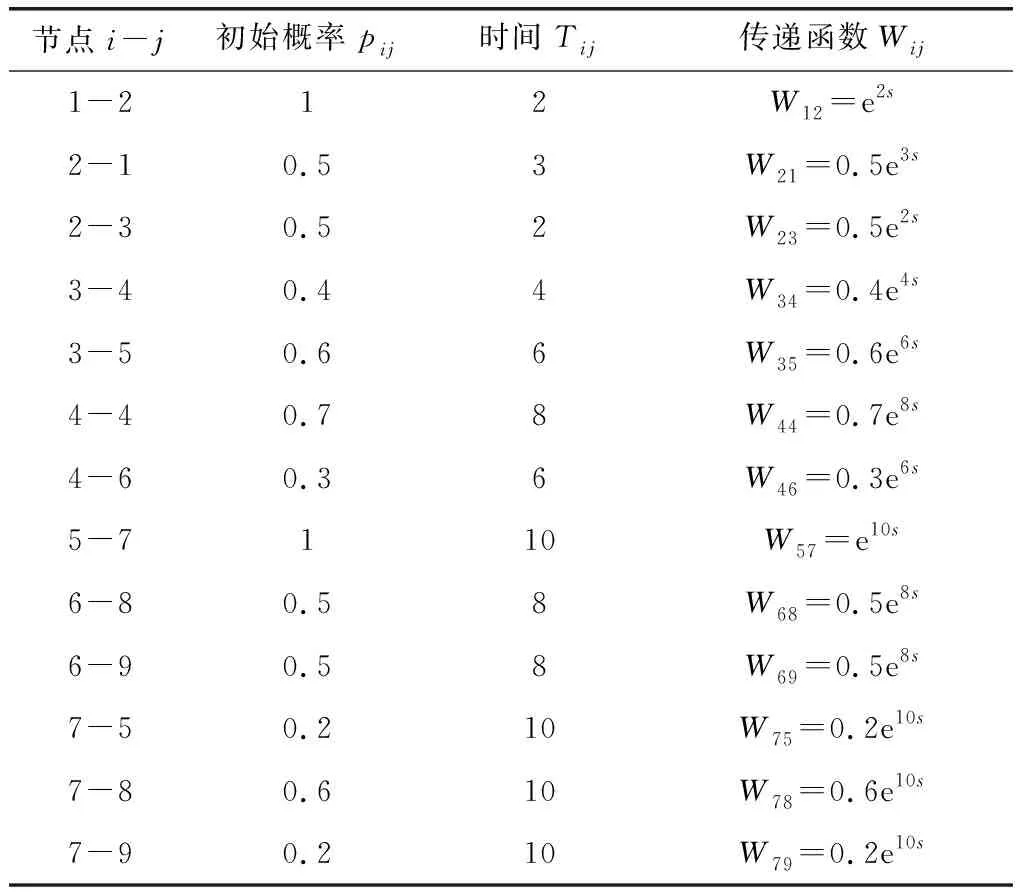
表1 活动初始传递概率与传递时间

步骤 3根据图9所示的AF-GERT网络依次对节点进行迭代学习。

步骤 3.1针对节点6与节点8、9间链路概率进行自学习。

根据定义5,节点6到节点8、9之间的等效传递函数WE68、WE69为WE68=W68=p68e8s和WE69=W69=p69e8s。

由式(5)、式(6)可得相应的等效传递概率与期望时间为pE68=p68,TE68=8和pE69=p69,TE69=8。

已知V8=200,V9=-100,当企业只考虑经济效益影响时,由式(14)可得网络传递效用值为F6=pE68×V8+pE69·V9=200p68-100p69。

当企业不仅考虑经济效益,还考虑传递时间影响时,由式(15)可得网络传递效用值为

根据式(16)、式(17)依次进行概率迭代学习,对节点6而言,可任选路径概率p68和p69进行迭代,当迭代路径概率p68时,p69=1-p68;当迭代路径概率为p69时,p68=1-p69。迭代学习的结果如图10所示,从中不难发现,无论迭代p68还是p69,最终的概率均衡值都相同。

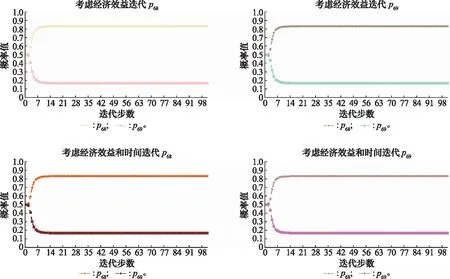
图10 节点6迭代概率图Fig.10 Iteration probability diagram of node 6

由此可得节点6最终的路径学习概率为p68=0.833 3,p69=0.166 7,节点概率达到均衡状态时,此时网络传递效用值即为节点6最终的效用值。因此,当企业只追求经济效益时,节点6最终的效用值为

V6=200×0.833 3-100×0.166 7=149.99

当企业不仅考虑经济效益,还考虑传递时间影响时,网络传递效用值为

步骤 3.2针对节点4与节点6间链路概率进行自学习 。

根据定义5,节点4到节点6之间的等效传递函数WE46为WE46=W46/(1-W44)=p46e6s/(1-p44e8s)

由式(5)、式(6)可得相应的等效传递概率与期望时间为

当企业只考虑经济效益影响时,此时由于pE46=1,该情况由p46代替pE46进行迭代计算。节点4的传递效用值为F4=p46·V6=149.99p46。

当企业不仅考虑经济效益,还考虑传递时间影响时,由式(15)可得节点4的传递效用值为

同样根据式(16)、式(17)依次进行迭代学习,迭代学习的结果如图11所示。

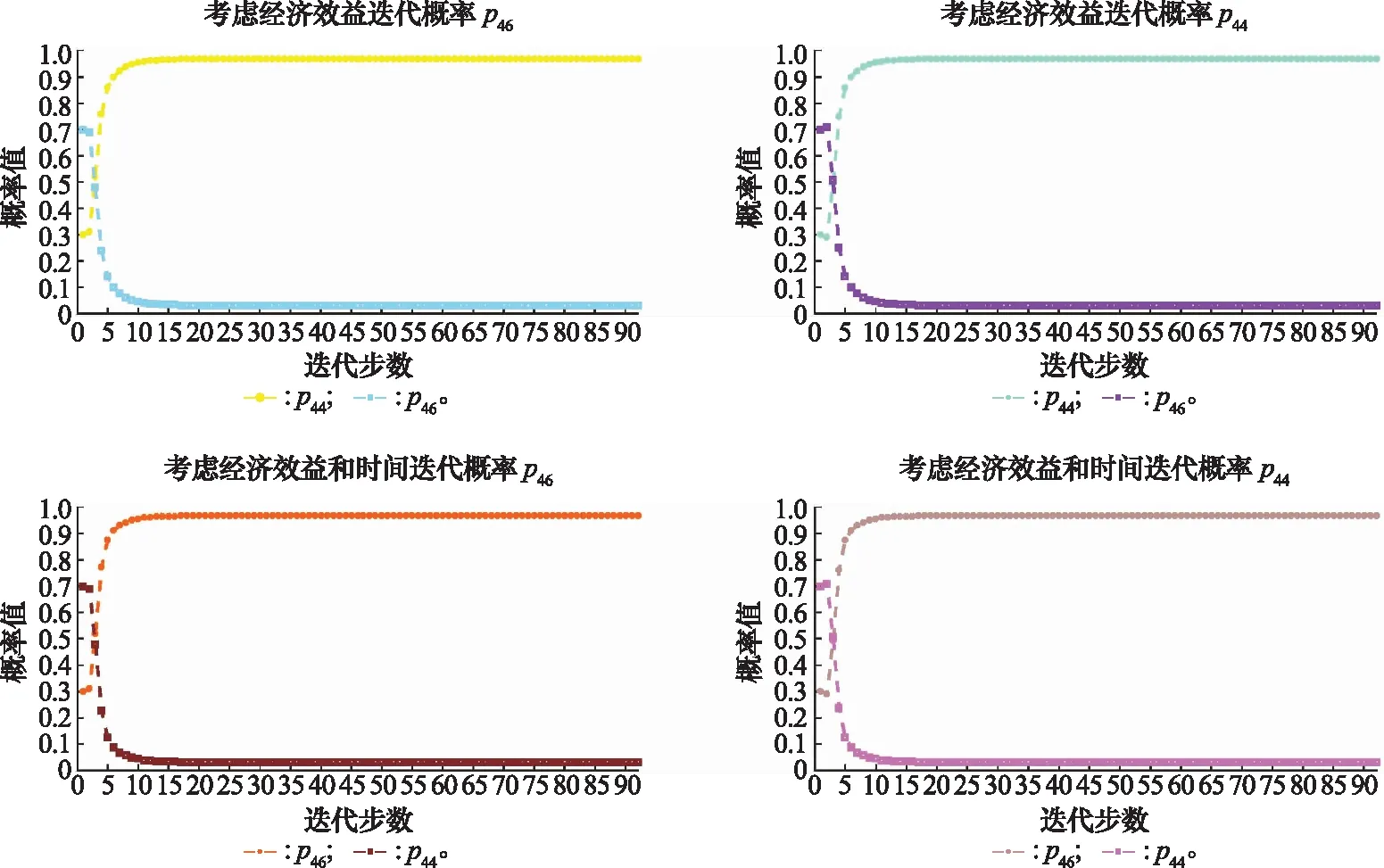
图11 节点4迭代概率值Fig.11 Iteration probability diagram of node 4

节点4最终的路径学习概率为p46=0.967 7,p44=0.032 3,当企业只追求经济效益时,节点4最终的效用值V4=149.99×0.967 7=95.802 3;当企业不仅考虑经济效益,还考虑传递时间影响时,节点4最终的效用值为

步骤 3.3针对节点7与节点8、9间链路概率进行自学习。

根据定义5,节点7到节点8、9之间的等效传递函数WE78、WE79为

由式(5)、式(6)可得相应的等效传递概率与期望时间为

当企业只追求经济效益时,由式(14)可得节点7的传递效用值为F7=200p78/(1-p75)-100p79/(1-p75);当企业不仅考虑经济效益,还考虑传递时间影响时,由式(15)可得节点7的传递效用值为F7=200pE78/TE78-100pE79/TE79=(200p78-100p79)/(10+10p75)。

根据式(16)、式(17)依次进行迭代学习,对节点7而言,可任选两个路径概率p75、p78和p79进行迭代,例如首先固定p78=0.6保持不变,当迭代路径概率为p75时,p79=1-0.6-p75,然后继续固定某路径概率保持不变(例如p79),迭代路径概率为p78时,p75=1-p79-p78,重复上述操作,直到路径概率达到均衡值。迭代学习的结果如图12所示。

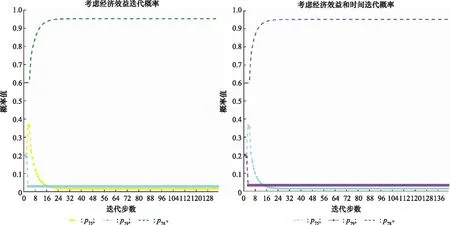
图12 节点7迭代概率值Fig.12 Iteration probability diagram of node 7

当企业只考虑经济效益影响时,节点7最终的效用值

此时V5=V7p57=190.690 8。

当企业不仅考虑经济效益,还考虑传递时间影响时,节点7最终的效用值为

此时V5=18.455 3/10=1.845 53。

步骤 3.4针对节点3与节点4、5间链路概率进行自学习。

根据定义5,节点3到节点4、5之间的等效传递函数WE34、WE35为WE34=W34=p34T34,WE35=W35=p35T35。

由式(5)、式(6)可得相应的等效传递概率与期望时间为pE34=p34,pE35=p35和TE34=4,TE35=6。

当企业只追求经济效益时,由式(14)可得节点3的效用值为

F3=p34V4+p35V5=95.802 3p34+190.690 8p35

当企业不仅考虑经济效益,还考虑传递时间影响时,由式(15)可得节点3的效用值为

根据式(16)、式(17)依次进行迭代学习,对节点3而言,可任选路径概率p34和p35进行迭代,迭代学习的结果如图13所示。

图13 节点3迭代概率值Fig.13 Iteration probability diagram of node 3

由此可得当企业只追求经济效益时,节点3最终的效用值

V3=95.802 3×0.090 9+190.690 8×0.909 1=182.065 4

当企业不仅考虑经济效益,还考虑传递时间影响时,节点3最终的效用值为

步骤 3.5针对节点2与节点3间链路概率进行自学习。

根据定义5,节点2到节点3之间的等效传递函数为WE23=W23/(1-W12W21)=p23e2s/(1-p21e5s)。

由式(5)、式(6)相应的等效传递概率与期望时间为pE23=p23/(1-p21),TE23=(1/pE23)·(∂WE23/∂s|s=0)=(2+3p21)/p23;当企业只追求经济效益时,由式(14)可得节点2的传递效用值为F2=182.065 4p23。

当企业不仅考虑经济效益,还考虑传递时间影响时,由式(15)可得节点2的传递效用值为F2=pE23V3/TE23=0.707 9p23/(2+3p21)。

根据式(16)、式(17)依次进行迭代学习,对节点2而言,可任选路径概率p23和p21进行迭代,迭代学习的结果如图14所示。

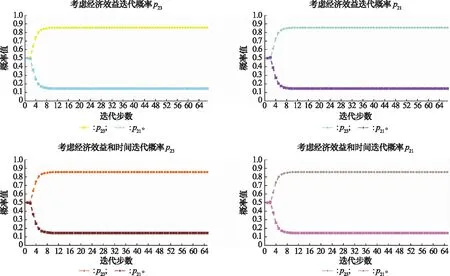
图14 节点2迭代概率值Fig.14 Iteration probability diagram of node 2

步骤 4各节点路径概率配置均衡解。

节点6、4、7最优的路径学习概率为p68=0.833 3,p46=0.967 7,p78=0.952 4;节点3最优的路径学习概率有两种情况,当只考虑经济效益时,p35=0.909 1,当考虑经济效益和时间时,p34=0.909 1;节点2最优的路径学习概率为p23=0.857 1。

步骤 5技术开发体系网络最优路径方案决策。

综上,当传递效用值只考虑经济效益驱动影响时,网络决策的最优路径为1-2-3-5-7-8;当考虑经济效益和完成时间影响时,网络决策的最优路径为1-2-3-4-6-8;并且智能节点经过学习,回路路径的传递概率大大减少,资源配置效率也相应提高。当系统主体只追求经济效益时,创新开发资源将逐渐流向技术B的开发,而当系统主体既考虑经济效益,又考虑完工时间时,创新开发资源将逐渐流向技术A的开发。

4.2 参数敏感性分析

文中涉及的参数主要包括初始概率增值Δp1以及刺激因子ξa、ξb,其中参数Δp1是启动迭代方程的引子,并不影响节点最终的概率均衡值。以节点6为例,对Δp1进行敏感度分析以说明其影响。

由图15可知,对于不同的初始概率增值Δp1=0.001,0.01,0.1,0.2,0.3,0.4,最终的概率均衡值不变,迭代步数也仅差1～2步。因此,Δp1的取值并不影响迭代过程。理论上,Δp1≤1-p0,但实际应用过程中,Δp1值不宜过大,否则不符合现实初始概率增加的情况,建议取值范围为0<Δp1≤0.1。

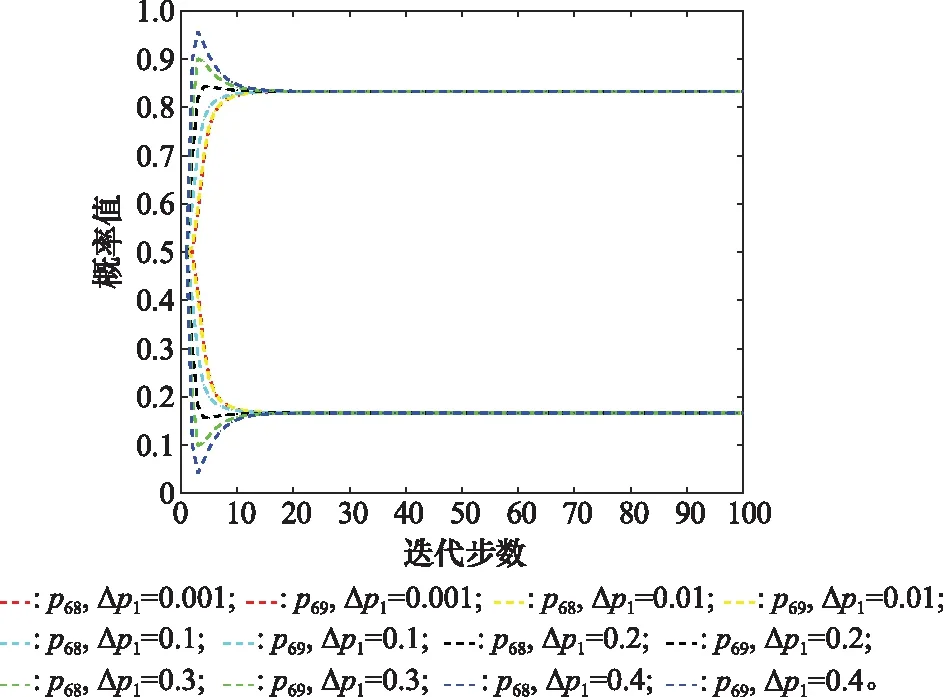
图15 节点6不同Δp1的敏感性分析Fig.15 Sensitivity analysis of different Δp1 for node 6

由推论2可知,正、负刺激因子的取值范围为0≤ξbi<ξai≤1且0≤ξaiξbi≤1/4。由定理4可知,均衡解为ξai/ξai+ξbi=ξai/ξbi/(1+ξai/ξbi),因此为了研究刺激因子的具体影响,针对不同的ξai/ξbi值,对节点刺激因子进行灵敏度分析,如图16～图18所示。

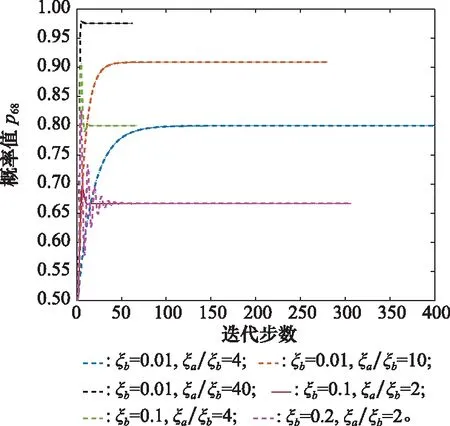
图16 节点6不同ξa和ξb的敏感性分析Fig.16 Sensitivity analysis of different ξa and ξb for node 6

图17 节点4和7不同ξa和ξb的敏感性分析Fig.17 Sensitivity analysis of different ξa and ξb for nodes 4 and 7

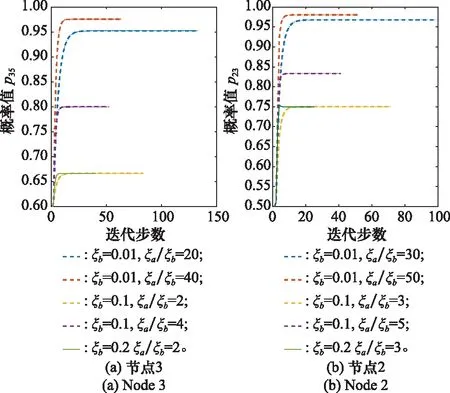
图18 节点2和3不同ξa和ξb的敏感性分析Fig.18 Sensitivity analysis of different ξaand ξb for nodes 2 and 3

由图16～图18所示,对于相同的ξb,ξai/ξbi的值越大,最优路径最终迭代的概率均衡值越大。这说明正刺激相对于负刺激的效应越大,最终的迭代效果也就越好。此外,对于相同的ξai/ξbi值,ξb越大,迭代曲线的波动会更大,这可能是因为负刺激因子的作用在破坏概率改进的过程。因此在实际应用过程中,应努力促进正刺激因子的改善,避免负刺激的产生。

4.3 对比分析

本节通过3种方式(不学习、固定激励系数学习、变激励系数学习)进行效果分析,其中固定激励系数学习指的是学习迭代方程中不考虑效用值的驱动影响,但学习迭代方程中仍保留方向函数的存在,方向函数保证了迭代方向的正确,如若不考虑方向函数,则在迭代错误路径概率时,该路径概率也会一直增加。由于迭代过程中涉及迭代步数以及迭代概率两个关键值,因此分别从达到均衡概率值的迭代步数以及迭代步数相同时迭代路径的概率两个角度进行对比分析。其中a表示固定激励系数学习(考虑经济效益);b表示固定激励系数学习(考虑经济效益和时间);c表示变激励系数学习(考虑经济效益);d表示变激励系数学习(考虑经济效益和时间)。

(1) 迭代步数对比分析

如表2以及图19所示,传递效用值无论是否考虑活动时间,变激励系数学习都比固定激励学习的迭代步数要少,说明考虑目标效益驱动影响可以加快学习迭代的速度。

表2 达到均衡解时的迭代步数对比

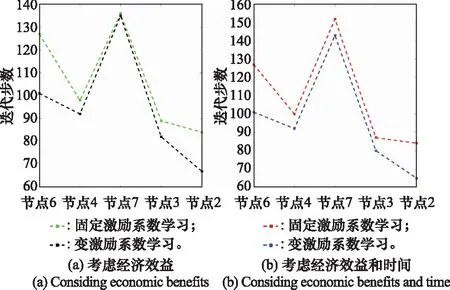
图19 迭代步数对比图Fig.19 Comparison diagram of iteration steps

(2) 迭代概率对比分析

为便于节点迭代路径概率的比较,不同学习方式取相同的迭代步数。例如,在变激励学习中节点6到节点8、9之间的路径概率迭代到第23步时,p68=0.833 3,p69=0.166 7,因此在固定激励系数学习中,取第23步时的路径迭代概率进行比较。不同学习方式的最优路径概率以及创新技术开发项目成功的期望概率、期望时间对比如表3所示。

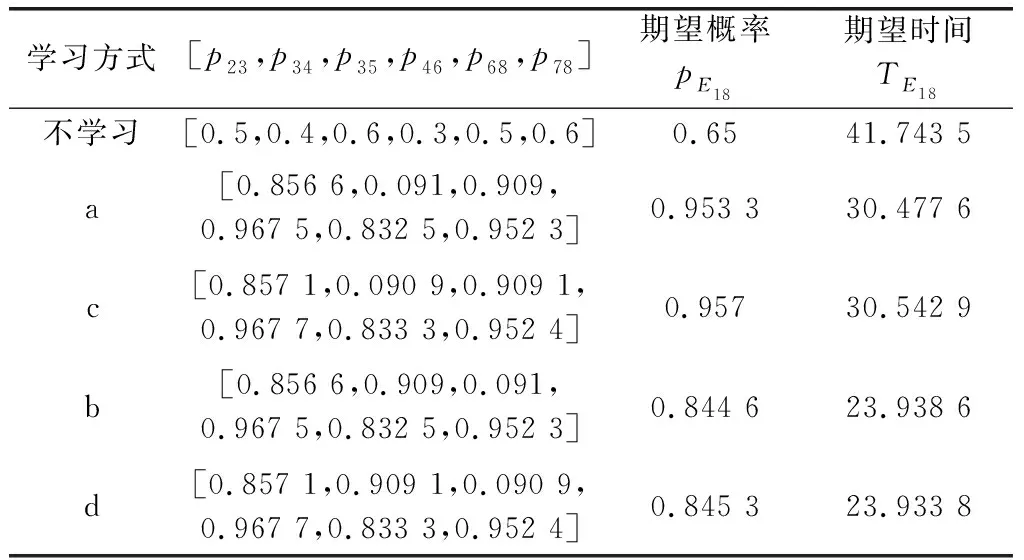
表3 不同学习方式迭代概率对比

根据表3可以看出,一方面,与不学习相比,经过学习后的最优路径概率均有不同程度的增加,成功的期望概率是不学习的1.3到1.47倍,完工时间也缩短了26.99%到42.66%。另一方面,当系统目标只考虑经济效益影响时,变激励系数学习比固定激励系数学习效果略有提高,成功的期望概率是固定激励系数学习的1.003 5倍;当系统目标考虑经济效益与完工时间影响时,变激励系数学习成功的期望概率是固定激励系数学习的1.001倍,完工时间缩短了0.02%。因此,变激励系数学习方式无论是在迭代步数还是迭代概率方面均有不同程度的改进。

(3) 与其他方法对比分析

文献[11]给出了GERT网络多目标决策的资源优化求解方法,与本文相比,文献[11]虽然改善了网络节点传递概率,指明了资源流动方向,但网络不具备学习能动性。经过案例数据计算,路径概率对比如表4所示,利用本文方法,最终的期望概率可提高10.89%,期望时间缩短26%。

表4 与其他方法迭代概率对比

综上所述,通过自身学习方式以及其他方法的对比分析,验证了基于A-GERT网络“刺激-反应”学习模型的合理性和有效性。

5 结束语

本文主要研究基于GERT网络的体系过程决策问题,例如在工程计划管理、产业价值流动以及作战编配体系等需要在不同阶段做出最优决策的体系活动中,GERT网络虽然可以很好地描述活动过程,但网络节点的决策模式较为静态单一,无法体现活动过程中决策的能动性。因此,首先以GERT网络为基础架构,构建Agent系过程A-GERT网络,结合改进的刺激-反应模型研究体系网络活动的概率学习机制。刺激-反应模型可通过输出反馈进行主动学习,具有良好的自适应性。此外,从目标效益驱动的角度出发,通过计算网络传递效用值改进刺激-反应学习迭代方程,构建A-GERT网络“刺激-反应”模型的学习决策机制。最后,以技术开发方案决策问题进行分析研究,结果表明,在管控措施激励以及不同的目标效益驱动下,传递概率会产生相应的动态变化,资源也会流向更优的技术开发路径。并且通过对比分析,该模型的效果更好。A-GERT网络“刺激-反应”模型的构建为解决体系网络过程学习决策问题提供了一种新思路。