改进螺旋桨敞水性能预报的泰勒展开边界元法

2022-08-17汤世昕沈育静陈纪康段文洋

哈尔滨工程大学学报 2022年7期

汤世昕，沈育静，陈纪康，段文洋

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001)

迄今为止已有多种理论或方法计算船舶螺旋桨的水动力性能，如螺旋桨的升力线理论、升力面理论及面元法等。螺旋桨升力线理论借鉴了机翼升力线理论，其基本方法是用一条从叶根到叶梢的涡线近似代替螺旋桨叶模型。但是由于其在理论上过于简化，不少学者相继发展了升力面理论加以完善。升力面理论把船舶螺旋桨等假定简化成为薄物体，即忽略了螺旋桨桨叶厚度的影响，因而该理论中的边界条件与真实的物面条件并不相同。而且由于桨叶薄翼在导边处的流体速度趋于无穷，使得该理论无法求解出位于导边附近的压力情况，限制了进一步对压力分布的预报和优化。面元法没有对螺旋桨的几何形状做任何假设，并在实际桨叶面上满足物面边界条件，因此用面元法不仅可以准确地预报螺旋桨的推力和转矩，而且可以较准确地预报螺旋桨表面的压力分布。

面元法最早由Hess等[1]提出和应用，用于求解三维不可压、无粘和无旋流体中的无升力体水动力问题。Morino[2]提出了速度势面元法，并将其应用至升力体的水动力计算中。随后Hoshino等[3-5]发展出了一系列基于速度势面元法的数值计算方法，分析普通螺旋桨、大侧倾螺旋桨以及导管螺旋桨的水动力性能。Maniar等[6-8]应用B样条曲线构建升力体的几何表面并使用高阶面元法，预报结果更为准确。此外董世汤等[9-12]国内学者为推动面元法在工程中的应用进行了研究以及数值验证工作。

现有的基于速度势的面元法称为常值面元法(constant panel method, CPM)，它假定面元上的速度势为常值，通常采用Morino方法计算影响系数，并使用Yanagizawa发展的插值方法获得物体表面的速度分布，这种速度计算方式可以有效减少对影响系数求梯度消耗的计算时间，但也会不可避免地导致数值误差。该误差在桨叶导边等几何变化明显的位置较大，并且最终导致常值面元法的精度下降[5]。

针对上述插值方法求解诱导速度的缺点，本文分别使用零阶和一阶泰勒展开边界元方法(taylor expansion boundary element method, TEBEM)求解诱导速度，预报螺旋桨定常水动力性能，并与插值方法的结果和实验值进行比较。随着计算机性能的提高，可以通过对影响系数求梯度获得物面速度，即零阶TEBEM的求解诱导速度方法。一阶TEBEM[13]对源偶混合分布方法中的偶极强度进行一阶泰勒展开，并将诱导速度作为未知数，在线性方程组中直接求解，可以有效提高物面突变处计算精度，从而改善桨叶导边、随边处压力分布预报。

1 螺旋桨定常水动力的定解问题

1.1 坐标系建立

对于在速度为VA的来流中以角速度Ω转动螺旋桨，采用如图1所示的固定于桨叶的坐标系[3]o-xyz，原点o固定于桨盘面的中心点，x轴沿螺旋桨的旋转轴指向下游，z轴沿螺旋桨某一叶片的母线，z轴与x轴和y轴组成右手坐标系。同时也采用一柱坐标系o-xrθ作为参考坐标系，其θ角度量由z轴起始逆时针旋转的角度[14]。

图1 螺旋桨坐标系Fig.1 Coordinate system of propeller

1.2 速度势与边界条件

流域的边界面S由物面SB(包括桨叶表面和桨毂表面)、尾涡面SW和外边界面S∞组成，且边界的法向量指向域内，如图2所示[15]。

图2 升力体及其周围流场Fig.2 Body and flow field around it

(1)

同时满足以下边界条件：

1)在物面上满足法向速度为零的运动边界条件：

2)假设尾涡面的厚度为0并通过它没有法向速度跳跃和压力跳跃，即：

式中下标+、-表示尾涡的上下面。

3)当外边界面极远时,其上的扰动速度趋于0：

故扰动势满足的定解问题为：

(2)

将边界条件式(2)代入式(1)，流场中场点P满足的边界积分方程可简化为:

(3)

式中V0=VA+Ω×r。

1.3 压力Kutta条件

式(3)中Δφ需要压力Kutta条件来决定，即在三维升力体问题中，应满足随边处叶面和叶背间的压力差为零：

假定沿螺旋桨桨叶径向网格数为NR，对于定常流动问题，尾涡面上Δφ沿尾流方向上是不变的，且每个桨叶泄出的尾涡片是相同的。只要确定与螺旋桨随边相接的尾涡面上的值(Δφ)j，j=1,2,…,NR，即决定了整个尾涡面上的Δφ。如果根据等压条件的离散格式：

(4)

同时令：

(ΔpT.E.)j=fj(Δφ1,Δφ2,…,ΔφNR)

j=1,2,…,NR

建立起对(Δφ)j的NR个方程。由于压力是未知变量φ的非线性函数，使方程组不能直接进行求解，故只能通过牛顿迭代法求解。

每次迭代得到(Δφ)j的值，可通过定解问题求解速度势，进而求解出物面上速度分布，再通过Bernoulli方程求出物面上压力分布及随边处压力差，重复上述流程直至式(4)成立。

1.4 螺旋桨水动力计算

利用Bernoulli方程：

(5)

桨叶压力分布确定以后，通过物面压力积分的方式得到螺旋桨所受推力和转矩[4]：

式中：n=(nx,ny,nz)为单位法向量；r=(x,y,z)为位置矢量。并得到压力积分离散形式为：

(6)

式中：ni=(nxi,nyi,nzi)为面元i控制点处单位法矢;ΔSi为面元i的面积;(xi,yi,zi)为面元i中心处坐标。此外还须考虑粘性力对推力及转矩的作用：

(7)

式中：vti=(vtxi,vtyi,vtzi)为面元i处局部速度;Cfi为粘性阻力系数，根据普朗特-许力汀平板摩擦阻力系数公式计算。因轴向坐标向下游为正，从而总推力、扭矩为:

(8)

2 常值面元法原理简述

将桨叶表面及桨毂表面总称为物面SB，共划分了N个面元，在尾涡面SW上共划分了N1个面元。将式(3)离散化并令场点P沿面元法线方向趋近于原点，即为常值面元法所求解的离散方程，i=1,2,…,N。

(9)

式中Δφ由压力Kutta条件决定。使用前文的迭代方法得到速度势，并使用Yanagizawa发展的插值方法得到桨叶表面速度分布，计算压力并得到水动力，具体的求解方法可参考文献[3]。注意式(9)中影响系数的求法没有采用Morino方法计算，具体的求法可参考文献[15-16]，在下文中将这种求解诱导速度的方法简称为插值法。

除了技术人员下基层、到田间面对面讲解油菜高产栽培技术外，农业部门还利用街天、农资打假等时机，加大宣传引导，让农户早知道，早受益。

3 泰勒展开边界元法原理

3.1 一阶TEBEM原理

(10)

式中i=1,2,…,N。

为了构造一阶TEBEM求解的边界积分方程，需要将式(3)离散，并考察垂直于法线平面内相互正交的2个方向上的一阶导数，将偶极强度展开式代入后令场点P沿面元法线趋近于原点可得[16]：

(11)

3.2 零阶TEBEM原理

零阶TEBEM可作为一阶TEBEM的特例，即零阶TEBEM将偶极看作均匀分布，并通过式(9)直接求解得到速度势。为了获得诱导速度，对式(3)中场点P考察垂直于法线平面内相互正交的2个方向上的一阶导数，离散化后令场点P沿面元法线趋近于原点可得：

(12)

随后根据式(5)计算压力，通过式(6)～(8)得到水动力结果。零阶和一阶TEBEM中影响系数的求法同样可参考文献[15-16]。

4 网格划分

4.1 桨叶划分

为获得离散方程的数值解，将桨叶表面沿着弦向和径向划分成一系列平面四边形单元，并在导边和随边及叶梢和叶根处进行网格加密。若R、RH分别为螺旋桨半径和毂径，弦向和径向分别采用余弦分割[10]:

式中：si为叶剖面上点至导边的弦向距离；cj为半径rj处叶剖面弦长；Nc为弦向划分次数；NR为径向划分次数，且NR1、NR2分别为[RH, 0.9R]、[0.9R,R]内的径向划分次数，故NR=NR1+NR2。又有βci和βrj满足：

4.2 尾涡形状及划分

在数值求解方程之前，首先确需定螺旋桨尾涡面的几何形状，由于尾涡面实际上事先未知，而且真实几何形状相当复杂，一般是建立一个尾涡几何模型来处理，用经验方法确定它的几何形状模型。

本文参考了文献[9]中的尾涡模型，尾涡在桨叶随边处以螺旋桨几何螺距角作为它的螺距角下泄，不考虑螺距沿轴向的变化，同时忽略径向的收缩，即尾涡面是一个径向变螺距的螺旋面。在划分尾涡网格时，沿着螺旋线进行等距划分，在靠近随边处进行网格加密。

5 数值结果与讨论

5.1 计算模型

使用3种诱导速度计算方法预报了DTMB4119、KP458桨的敞水性能，并与实验结果进行比较。螺旋桨的主要几何参数列于表1中。

表1 螺旋桨的主要几何参数Table 1 Geometrical parameters of propellers

5.2 网格收敛性分析

网格收敛性主要包括桨叶网格收敛性、尾涡网格收敛性和尾涡长度收敛性。其中桨叶网格数为NC×(NR1+NR2)，尾涡网格数为NR×NW(NW为沿螺旋线划分次数)。实际数值计算时，在尾涡面泄出一定距离后将其截断；尾涡面长度LW指螺旋面沿x轴的长度，需要考虑其对数值结果的影响。

将DTMB4119作为计算模型，以一阶TEBEM为例验证数值结果的收敛性，表2～3给出了尾涡收敛性情况，表4给出了桨叶网格收敛性情况。首先在给定桨叶网格数(NC=28、NR1=18、NR2=5)后，通过改变尾涡划分次数NW，在不同进速系数工况下，发现当尾涡长度不小于1.4D(D为螺旋桨直径)时，尾涡长度对计算结果几乎无影响，故选择尾涡长度LW为1.4D，尾涡网格数为23×58(NR=23,NW=58)。

表2 尾涡网格收敛性(J=0.7,NC=28,NR1=18,NR2=5)Table 2 Convergence of the wake panels (J=0.7,NC=28,NR1=18,NR2=5)

表3 尾涡网格收敛性(J=0.9,NC=28,NR1=18,NR2=5)Table 3 Convergence of the wake panels (J=0.9,NC=28,NR1=18,NR2=5)

表4 桨叶网格收敛性(J=0.7，尾涡网格数为23×58，尾涡长度1.4D)Table 4 Convergence of the blade panels (J=0.7， wake panels are LW=23×58，LW=1.4D)

对于桨叶网格划分，在确定尾涡划分方式后，发现当桨叶网格数选择NC=28、NR1=18、NR2=5时，计算结果基本收敛，故在随后的计算中均采用这种桨叶划分方式，面元分布情况及尾涡如图3所示。

图3 离散网格局部坐标系Fig.3 Sketch of the local coordinate system

用同样的方法分析插值法和零阶TEBEM的收敛性情况，计算收敛时插值法选择桨叶网格数为36×52(NC=36、NR1=42、NR2=10)，尾涡网格数为52×58(NW=58)，尾涡长度LW为1.4D。零阶TEBEM择桨叶网格数为33×36(NC=33、NR1=28、NR2=8)，尾涡网格数为36×58(NW=58)，尾涡长度LW为1.4D。

5.3 数值结果分析

本文3种数值方法对DTMB4119螺旋桨的计算结果与实验值[17]及其他研究所的结果比较如图4所示。根据目前的计算结果，对于推力系数，3种方法的结果相近，且精度相当；随着进速系数的改变，呈现出线性变化的特点；对于转矩系数，零阶和一阶TEBEM的结果大于插值法的结果，且更接近实验值，随着进速系数的减小，3种方法计算的误差会稍大一些。但总体来讲，零阶和一阶TEBEM的结果与实验值有较高的一致性，且在设计点附近的精度要稍高于其他的计算结果。CSSRC[9]与MHI在预报螺旋桨定常性能时采用了不同的面元形状及影响系数计算方式，因此使用插值法计算速度得出的最终结果与本文用插值法结果有一定差异。

图4 DTMB4119的敞水性能Fig.4 Open water performance of DTMB4119

图5 DTMB4119网格示意Fig.5 Panel arrangement for DTMB4119

DTMB4119桨的桨叶表面压力分布由Jessup在文献[18]中给出，通过激光测速仪测得桨叶表面的速度分布，然后由Bernoulli方程换算得到表面压力分布。该实验结果一直被用来作为校验计算方法的标准依据。图6～7给出了4119桨在设计点J=0.833下桨叶表面压力分布的实验值与3种数值计算方法的结果比较。

图6 r/R=0.7处压力分布Fig.6 Pressure distribution at r/R =0.7

图7 r/R=0.9处压力分布Fig.7 Pressure distribution at r/R =0.9

通过0.7R处压力分布与实验值的比较，可以看到3种方法得到的结果与实验值在大部分范围内吻合较好；使用零阶和一阶TEBEM得到的压力系数在叶背及叶面接近导边处变化程度较大，即流体速度发生了明显的变化；从实验结果中也可以观察到相同的特征，通过插值法得到的压力变化更加平滑，导致产生误差而无法体现出上述变化特征。类似地，在0.9R处压力分布的比较上，零阶和一阶TEBEM得到的压力分布更接近实验结果，因此在压力积分的结果上，零阶和一阶TEBEM所得转矩系数更大，且接近于实验值。

图8～9为3种方法所得压力系数-CP分布的云图，可以看出差异主要位于导边和随边处，在其余的位置结果接近。

图8 叶面压力系数分布Fig.8 Pressure coefficient distribution on the upper surface

图9 叶背压力系数分布Fig.9 Pressure coefficient distribution on the lower surface

图10～11中比较了3种方法在紧靠导边的面元沿径向的压力分布情况；图12中比较了紧靠随边的面元沿径向的压力分布情况。尾涡网格划分时，3种方法均选择NW=58、LW=1.4D；桨叶划分时，均采用NC=32，NR1=21，NR2=6。零阶和一阶TEBEM得到的压力分布在导边、随边处有相似的变化趋势，且一阶TEBEM的压力系数结果较小；插值法结果在导边处的大部分范围内与前两者都有明显的差异，即插值法引起与实验值的误差；在接近叶梢的位置，3种方法的预报结果均向低压快速变化，可能是未考虑空化的影响。同时参考图6～7中0.7R、0.9R处导边和随边的压力分布实验值，发现一阶TEBEM结果的误差更小，因此相比于零阶TEBEM，局部压力预报的精度更高一些。

图10 叶面导边处压力分布Fig.10 Pressure distribution at the leading edge on the upper surface

图11 叶背导边处压力分布Fig.11 Pressure distribution at the leading edge on the lower surface

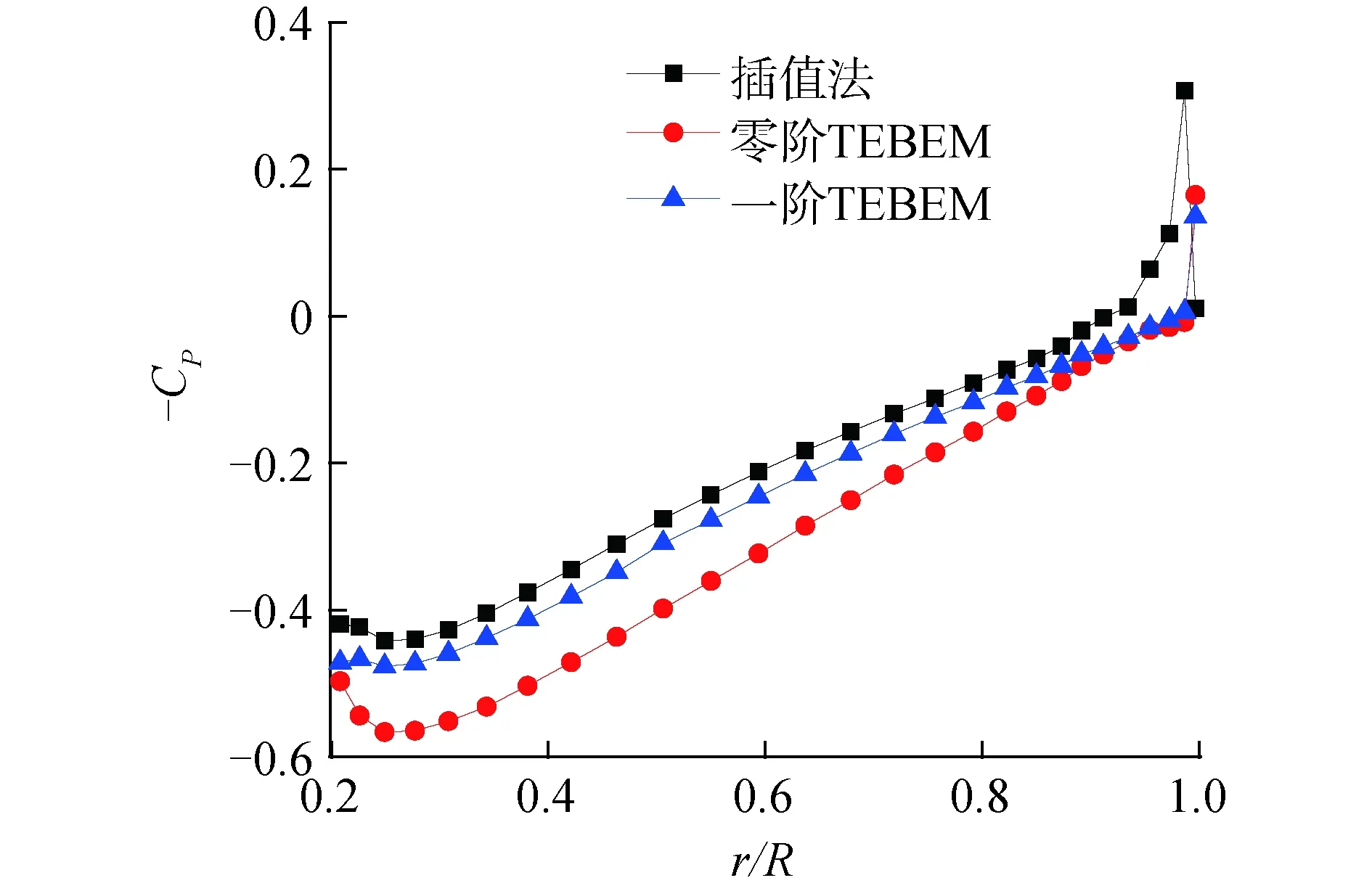
图12 随边处压力分布Fig.12 Pressure distribution at the trailing edge of the blade

为了进一步分析3种诱导速度计算方法的求解精度，选择了常见的KP458桨进行计算比较。相较于无纵倾、侧倾的三叶桨DTMB4119，KP458桨在各桨叶剖面处具有不同程度的侧倾，在几何形状上更为复杂。在尾涡网格划分时，3种方法均选择NW=58、LW=1.4D；桨叶划分时，一阶TEBEM采用NC=28、NR1=18、NR2=5；零阶TEBEM采用NC=28、NR1=25、NR2=8；插值法采用NC=36、NR1=42、NR2=10。螺旋桨网格划分示意图如图13所示，计算结果与实验值的比较见图14～15。采用零阶和一阶TEBEM来计算具有不同几何特征的螺旋桨敞水性能，推力系数的精度相近，而转矩系数的计算精度相比于插值法有明显的提升，误差减少近10%。