基于多尺度稀疏简单循环单元模型的水声目标识别方法
2022-08-17杨爽曾向阳
杨爽, 曾向阳
(西北工业大学 航海学院,陕西 西安 710072)
水声目标识别是水声信号处理领域的重要研究方向和难题之一。由于复杂海洋环境中噪声的影响,实验室仿真效果很好的识别方法应用于现实场景时,效果可能不如预期。因此,抑制噪声干扰、提高识别方法的鲁棒性对于识别方法的实际应用非常关键。
传统水声目标被动识别系统中,特征提取和分类器通常是相对独立的2个环节,因而噪声抑制或依赖于信号预处理,或在特征提取环节进行。其中,预处理方面的降噪方法已有大量的研究;在特征提取环节,也有一些抗噪特征提取方法。陆晨翔等[1]提出水下目标信号的结构化稀疏特征提取方法,可借助稀疏贝叶斯学习模型,利用相邻帧样本间的相关性信息增强窄带线谱成分,在噪声失匹配条件下,能够保持较高的识别率。连梓旭[2]提出了基于Gammatone频率倒谱系数的水声目标特征提取方法以及基于Gammatone滤波器组与子带瞬时频率的水声目标特征提取方法。这2种方法能够有效地提升水声目标识别系统的性能,具有较强的鲁棒性。
近几年,深度学习(deep learning,DL)理论广受关注,也为水声目标识别技术提供了新的思路[3]。王强等[4]研究了深度学习方法在水声目标识别中的适用性,建立卷积神经网络(convolutional neural networks, CNN)和深度置信网络(deep brief networks,DBN)模型。3种实测水声目标的识别结果表明,利用深度学习模型进行水声目标识别是一种可行的途径。卢安安等[5]将长短时记忆(long short-term memory,LSTM)网络应用于水声目标识别。LSTM 结构在梅尔频率倒谱系数(mel frequency cepstral coefficient, MFCC)特征上的识别效果要优于常规的循环神经网络(recurrent neural networks, RNN)、CNN和深度神经网络(deep neural networks, DNN),说明网络利用更多的时序信息往往会取得更好的效果。但是,LSTM网络的前后依赖导致RNN并行计算较为困难,所以其计算速度远没有CNN快。Tao Lei等[6]基于对LSTM模型的研究,提出了简单循环单元(simple recurrent unit, SRU),在自然语言处理(natural language processing, NLP)任务方面证明了SRU的有效性。在分类和问题回答数据集上,SRU比cuDNN优化的LSTM加速5~9倍。
本文将SRU方法引入水声目标识别,利用深度学习端到端的处理能力,基于孟庆昕等[7]的研究,利用原始时域波形对目标进行分类识别,时域波形结构特征隐含了音色信息。在此基础上,提出一种多尺度稀疏SRU模型,通过与CNN模型的对比实验,检验其识别性能。
1 简单循环单元
RNN权重系数是共享的,即在一次算法迭代中,循环节点使用相同的权重系数处理所有的时间步[8]。对于单向RNN,循环节点中不同的时间步所学习到的特征依赖于当前时间步前的所有时间步的输入和隐含状态,所以,每个时间步所学习到的时间长度是不同的。RNN结构如图1所示。

图1 RNN结构Fig.1 Structure of RNN
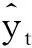
常规的RNN网络是串行结构,当前层的计算必须等到上一层完全执行完毕后才可以开始,严重限制了网络的运算速度。为了解决这一问题,Tao Lei等[6]提出了一种具有并行计算和序列建模能力的SRU网络。
单层SRU的计算为:
ft=σ(WfXt+vf⊗ht-1+bf)
(1)
rt=σ(WrXt+vr⊗ht-1+br)
(2)
(3)
(4)
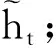
SRU能够并行运算的关键在于前一时刻隐含状态ht-1的使用方式。在门控循环单元(gated recurrent unit, GRU)网络中,ht-1与参数矩阵相乘来计算2个门控的隐含状态,门控状态的每个维数都依赖于ht-1的所有项,而计算必须等到ht-1完全完成后才能进行。SRU网络为了便于并行计算,式(1)和式(2)使用vf⊗ht-1、vr⊗ht-1这种点乘的方式代替矩阵相乘,通过这种简化,隐含状态的每个维数都变得独立,因此SRU网络中大部分计算是可并行的。这种并行结构提高了SRU计算速度。
2 多尺度稀疏SRU模型
受到特征融合在丰富分类特征信息方面的优势启发,提出了基于多尺度稀疏SRU的融合深度神经网络用于水声目标辐射噪声分类识别。深度网络通过多层隐层学习输入数据的特征表达,不同隐层学习到的特征是不同的,这些特征可以被认为是输入数据不同的特征表达形式。网络底层获取低层次特征,顶层学习高层次特征。越低层次的特征越能反映数据的局部特性,高层次的特征则具有抽象性和不变性。受到CNN模型Inception[10]架构的启发,网络不是单纯地通过增加模型的深度和宽度提高网络的表达能力,而是可以通过一种非均匀的稀疏结构来实现多尺度的特征表达。
这种多尺度的特征表达也可以应用于RNN网络中。SRU作为一种可并行的RNN,同时具备了时间序列建模能力和计算成本低的优点。本文将多尺度的特征表达应用在SRU中,提出了一种多尺度稀疏SRU模型,利用不同层SRU学习到的不同特征表达,对输入数据多尺度的特征进行融合,将融合后的特征组合作为分类器(模型顶层)的特征输入,完成多类目标的分类识别任务。
多尺度稀疏SRU模型框架结构如图2所示。图2(a)是模型的总体架构,由输入层、4个SRU块、多特征层(特征融合层)和1个全连接层构成。图2(b)是SRU块结构,每个SRU块都由一个n(n=1,2,3,4) 层堆叠的SRU网络和一个层标准化(layer normalization, LN)构成。LN多用于RNN网络中,在通道方向上对目标输入进行归一化操作,保证数据在通道方向上分布一致。同时,每个SRU块在模型输入和多特征层间添加跳跃连接,构成了网络的局部构造。跳跃连接多应用于较深的网络结构中,比深度模型直接学习输入和输出之间的映射更容易收敛,同时解决了SRU在训练过程中的梯度消散问题。4个SRU块中的SRU分别为1层、2层、3层和4层;隐含节点数分别为16、32、64和256。每个SRU块内部结构都是全连接的、非稀疏的,4个SRU块之间则是稀疏连接的。可以将4个SRU块理解为稀疏连接的滤波器组,将4个滤波器组连接成一个单一的输出向量,形成下一阶段的输入,即将4个SRU块的输出合并构成多特征层,多特征层包含不同层SRU学习到的特征表达。批量标准化(batch normalization, BN) 操作应用于多特征层之后,通过对数据批次归一化,加快网络收敛速度,同时防止网络的梯度消失和梯度爆炸。模型顶层连接一层全连接层。全连接层作为判别层输出各类水声目标样本的实际输出(概率)。
3 实验与分析
3.1 实测水声数据的处理
实验基于实际海域测试得到的3类水声目标(舰船、商船及某水下目标)数据,采样频率均为8 kHz。每类水声目标数据包含 15 个片段,每个片段的声音长度截取5 s。首先对水声目标数据进行预处理。对每段目标数据分帧,每帧长为100 ms,帧移为0,即每0.1 s的目标数据为一个样本,总计3类目标共2 250个样本。目标数据被严格地被划分为训练集、验证集和测试集。使用总样本的3/5作为训练,1/5作为验证,1/5作为测试。表1中总结了3类水声目标样本的统计数量。将3类目标的训练数据和验证数据进行标准化处理(零均值化同时方差归一化),消除声源距离远近对目标样本的影响,提取它们的时域波形作为网络模型的输入,构建时间序列网络模型。测试时,为了构建噪声失匹配条件,分别给3类目标测试数据加带限白噪声,生成SNR分别为-20、-15、-10、-5、0、5、10、15和 20 dB的测试数据,再对测试数据进行标准化处理。
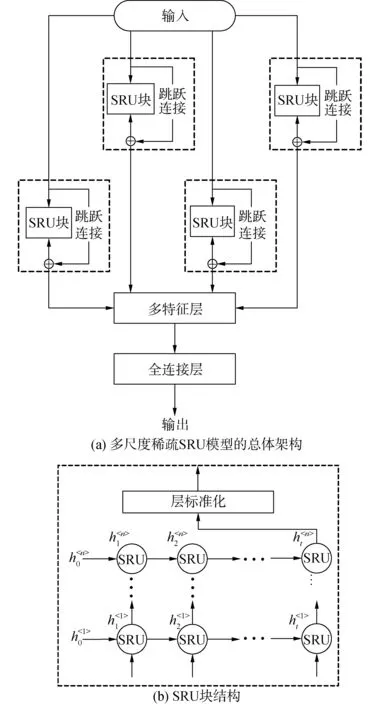
图2 多尺度稀疏SRU模型Fig.2 Multi-scale sparse SRU model

表1 3类水声目标样本数量Table 1 Number of samples of three types of underwater acoustic targets
3.2 对比方法和参数设置
本文使用3种模型与提出的网络模型进行对比:1)多尺度稀疏SRU模型(未加跳跃连接);2)多层SRU模型;3)多层CNN模型。其中模型2)和模型3)的架构和参数设置在下面分别进行介绍。
3.2.1 多层SRU模型
图3是多层SRU模型架构,由输入层、4层堆叠SRU和2个全连接层构成。模型中,4层堆叠SRU的隐藏节点数设为256,每层SRU后都添加了随机失活(dropout)层防止网络过拟合,网络单元的随机失活概率为0.1。第1个全连接层使用ReLU作为激活函数,激活前使用BN操作对输入数据进行批量归一化。第2个全连接层作为判别层输出各类水声目标样本的实际输出(概率)。

图3 多层SRU模型Fig.3 Multi-layer SRU model
3.2.2 多层CNN模型
图4是多层CNN模型架构,由输入层、3个一维卷积层、3个一维池化层和2个全连接层构成。模型中,每层卷积层进行ReLU激活,激活前都执行BN操作,后加一维池化层来降低数据的空间尺寸。3个一维卷积层中卷积核的大小为3,数量分别为32、64和128,一维池化层中卷和核的大小为3。第1个全连接层使用ReLU作为激活函数,激活前使用BN操作对输入数据进行批量归一化,激活后添加随机失活层防止网络过拟合,网络单元的随机失活概率为0.5。第2个全连接层作为判别层输出各类水声目标样本的实际输出(概率)。
3.3 评价指标
完成模型构建后,需要对模型进行训练(训练过程包括验证)和测试。其中,训练过程的评价指标是损失(loss)和正确识别率(accuracy),测试过程的指标是F1值。
网络模型中损失函数用来衡量网络模型的实际输出(概率)和期望输出(概率)之间的差异(误差)。网络模型在训练过程中,首先进行前向传播计算实际输出(概率),再通过反向梯度传播算法更新网络参数,降低损失函数的损失值来不断减小误差,使模型的实际输出(概率)越来越接近期望输出(概率)。因此网络训练过程中计算获得的损失值越小,网络模型的识别性能越好。4种网络模型的训练均采用稀疏分类交叉熵损失函数来计算损失,采用自适应力矩估计(adaptive moment estimation, Adam)算法优化梯度,学习率为0.001。正确识别率是正确分类的水声目标占所有水声目标的百分比。

图4 多层CNN模型Fig.4 Multi-layer CNN model
对训练好的网络模型进行测试时,使用F1值对网络模型进行误差度量。F1值的定义为:
(5)
其中:
式中:TP为预测是目标i(i=1,2,3)实际也是目标i的个数;FN为预测不是目标i实际是目标i的个数;FP为预测是目标i实际不是目标i的个数;TN为预测不是目标i实际也不是目标i的个数。P为查准率(所有预测是目标i的目标中,实际是目标i的比例),R为召回率(所有实际为目标i的目标中,成功预测为目标i的比例)。F1值可以看作是P和R的加权平均值。本文使用F1值评价不同算法的优劣。F1值越高,算法性能越好。
3.4 实验结果和分析
3.4.1 网络模型的训练
4种模型的输入都是不添加额外噪声的水声目标时域波形。模型的训练和验证都在GPU上进行,使用cuDNN来加快模型的训练速度。图5~8分别是4种模型损失和正确识别率随训练次数的变化曲线。表2是4种模型的验证结果和每次训练的花费时间。

图5 多尺度稀疏SRU模型损失和正确识别率随训练次数的变化曲线Fig.5 Losses and accuracy of the multi-scale sparse SRU model on classification

图6 多尺度稀疏SRU模型(未加跳跃连接)损失和正确识别率随训练次数的变化曲线Fig.6 Losses and accuracy of the multi-scale sparse SRU model without skip connections on classification

图7 多层SRU模型损失和正确识别率随训练次数的变化曲线Fig.7 Losses and accuracy of the multi-layer SRU model on classification
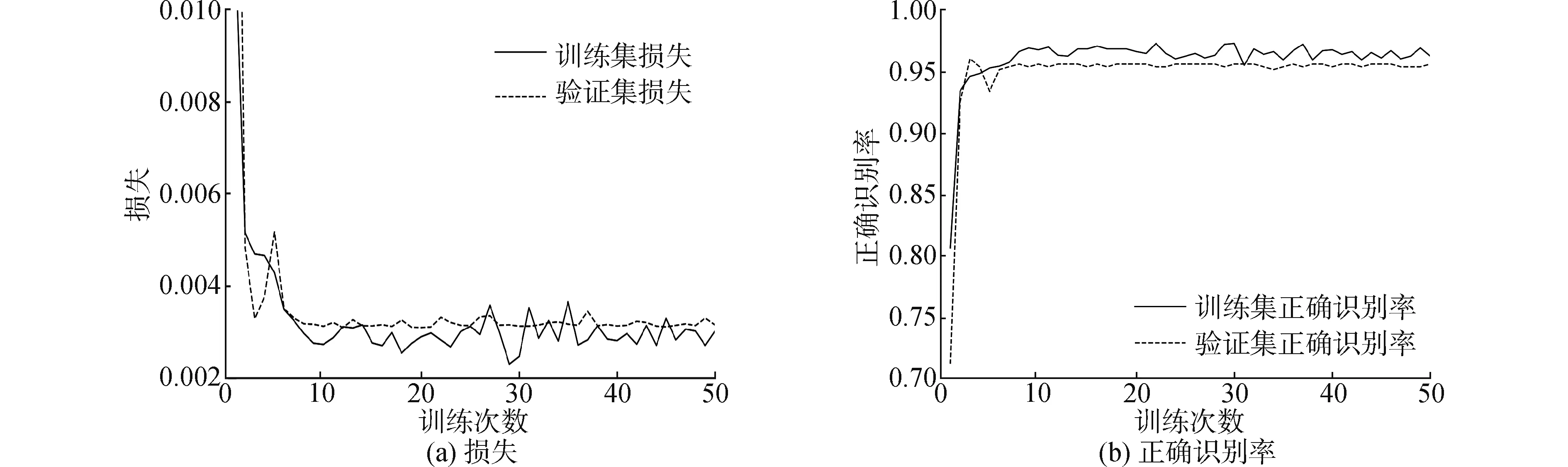
图8 多层CNN模型损失和正确识别率随训练次数的变化曲线Fig.8 Losses and accuracy of the multi-layer CNN model on classification
从图5~8的(a)可以看出,随着训练次数的增加,模型损失均收敛。其中多层CNN模型的训练损失波动较大,可能会影响网络的稳健性。从图5~8的(b)中可以看出,随着训练次数的增加,训练集和验证集的正确识别率都趋于稳定。其中,多尺度稀疏SRU模型训练到第6次时模型参数已达到最优,获得了验证集最优正确识别率。与之相比,未加跳跃连接的多尺度稀疏SRU模型训练到第22次时获得了验证集最优正确识别率,因此添加跳跃连接使得模型收敛加快,减少模型训练时间。
综合表2的内容可以看出,多尺度稀疏SRU模型(未加跳跃连接)的正确识别率和损失是最优的。多层SRU模型通过简单的堆叠SRU,很难获得与多层CNN相媲美的正确识别率。除此之外,3种SRU模型每次训练花费的时间都多于多层CNN模型。即SRU虽然弱化了RNN网络中的前后依赖结构,但是算法中仍然存在反馈,使得训练不能完全并行,导致训练时间较多层CNN模型长。
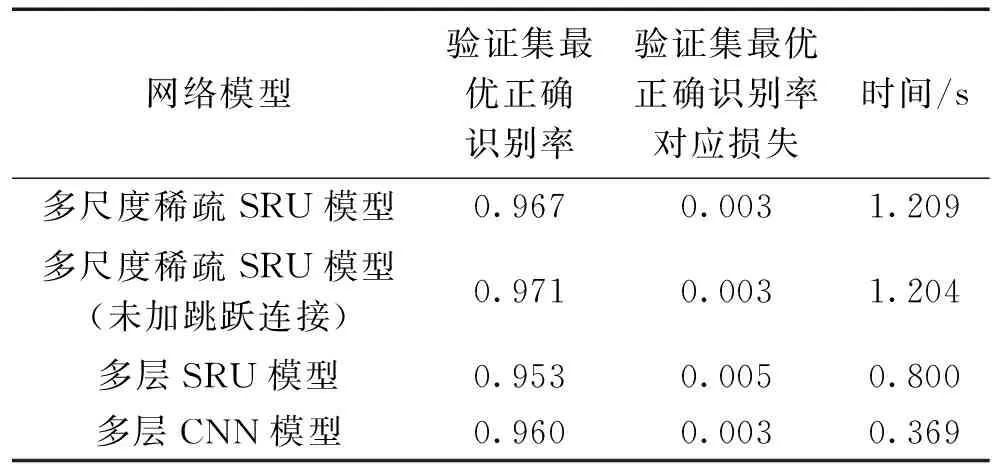
表2 4种模型的验证结果和每次训练花费时间Table 2 Validation results of the four models and the processing time per epoch
3.4.2 噪声失匹配条件下网络模型的测试分析
为了测试网络模型在噪声失匹配条件下的识别性能,将训练好的4种网络模型应用于噪声失匹配条件下的水声目标分类识别任务,对模型进行进一步分析。3.1节中为了构建噪声失匹配条件,分别给3类水声目标测试集数据加带限白噪声,生成SNR分别为-20、-15、-10、-5、0、5、10、15和 20 dB的水声目标数据。现将不同SNR条件下测试集数据的时域波形作为网络模型的输入,对4种网络模型的分类识别性能进行测试。
图9为不同SNR下,4种模型的F1值变化曲线,“未加噪声”标注表示测试样本不添加额外的带限白噪声,和训练样本保持同一噪声环境的情况。可以看出,3种SRU模型的F1值在SNR小于5 dB时均高于多层CNN模型。提出的多尺度稀疏SRU模型的F1值在SNR小于15 dB 条件下高于多层CNN模型,在SNR为20 dB和“未加噪声”条件下与多层CNN模型相同。同时可以看出,跳跃连接对噪声失匹配条件下多尺度稀疏SRU模型F1值的影响甚微。
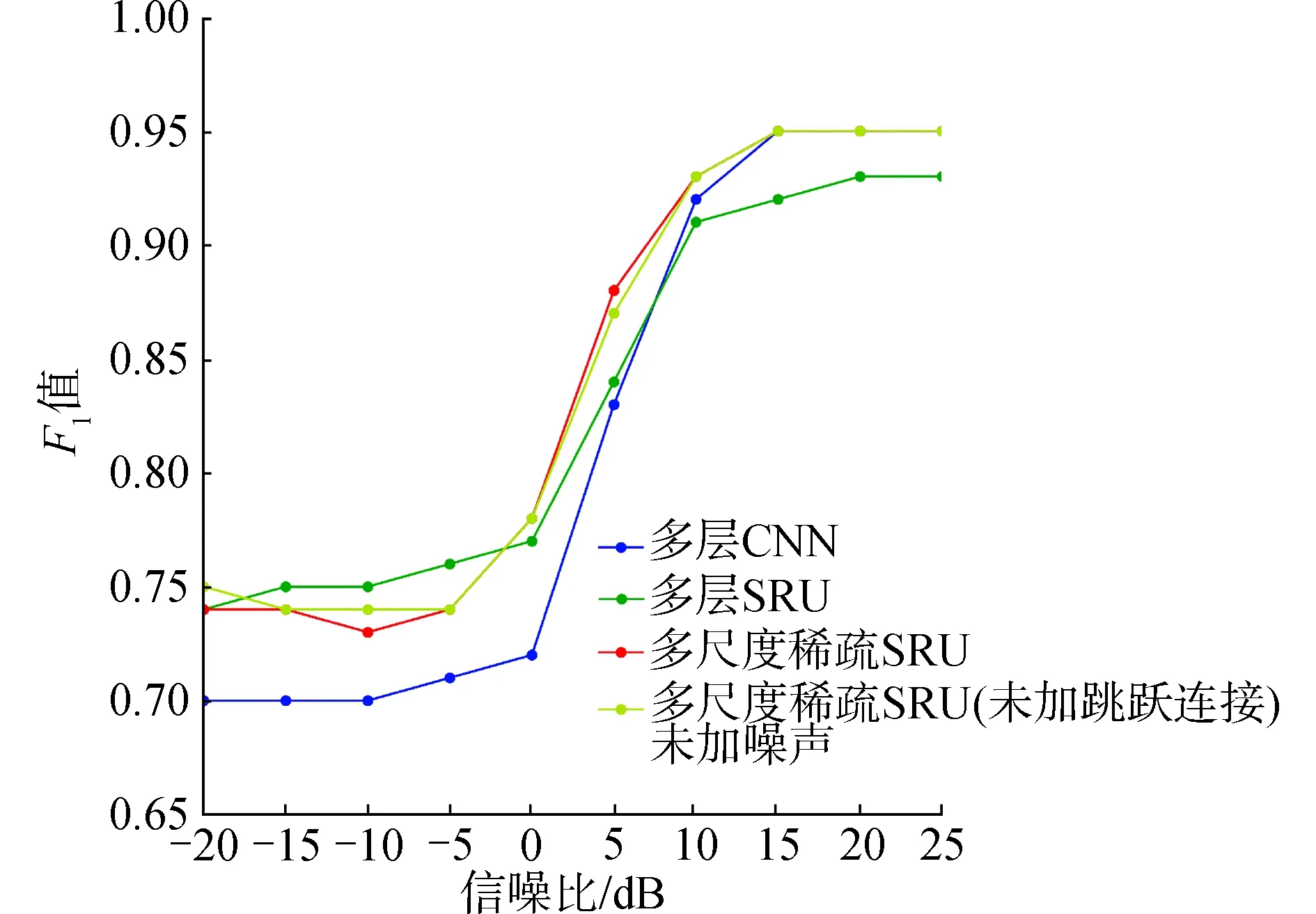
图9 4种模型的F1值Fig.9 F1 scores of the four models
水声目标的时域波形本质上是时间序列信号,包含了幅度和相位信息,信息保留完整,其生成和感知都是一个动态的层次。时间序列信号具有时间上的相关性,即相邻帧信号甚至长距离帧之间特征相关。对于SRU,网络提取的时间特征和由时间延迟产生的历史隐层状态共同输入给隐层产生当前状态和输出。因此网络最后时刻的输出和所有时刻的输入是相关的,是所有时刻输入的相关函数[11]。4种网络模型的测试结果表明,SRU能够利用水声时域波形时间上的相关性,生成具有噪声鲁棒的内部特征表示,从而使得SRU能够适应复杂的噪声环境,抑制噪声失配带来的影响。提出的多尺度稀疏SRU模型对不同层的SRU进行并联,获得了多尺度的特征信息,使得网络模型在获得更高F1值的同时能够抑制噪声的干扰。
4 结论
1)本文提出的多尺度稀疏SRU模型对不同层数堆叠的SRU块并联,获得多尺度的特征信息,使得网络模型获得了较高正确识别率;同时提出模型的F1值在低SNR下高于多层CNN模型,说明提出的模型能够抑制噪声失匹配带来的影响。
2)通过4种网络模型的对比实验发现,3种SRU模型的F1值在SNR小于5 dB时均高于多层CNN模型。说明SRU这种循环神经网络在低SNR条件下有能力生成具有噪声鲁棒的内部特征表示。
3)3种SRU模型每次训练花费的时间都多于多层CNN模型,所以在面向实际应用时需要考虑如何缩减训练时间。提出的多尺度稀疏SRU模型在输入层和多特征层(特征融合层)之间添加跳跃连接,加快了模型收敛,减小了训练时间。
循环神经网络由于具有内部反馈机制,擅长处理序列信号。水声目标时域信号是一个典型的包含幅值和相位信息的序列信号,其波形结构特征隐含了音色信息,所以本文从最原始的时域波形入手,研究提出的具有内部反馈机制的网络模型对序列数据在噪声失匹配条件下的适应性问题。在后续的研究中,将提取时域波形结构特征,与提出的模型联合,进一步研究分类识别系统的性能。
