基于功能图的作战体系关键节点分析

龚建兴, 朱 雷, 王华兵, 丁佩元, 路程昭

(1. 国防科技大学智能科学学院, 湖南 长沙 410073;2. 电子信息系统复杂电磁环境效应国家重点实验室, 河南 洛阳 471003)

0 引 言

现代战争已经由单一兵种的作战演化为体系之间的对抗,敌我双方通过信息系统将不同的作战要素融合为一个有机整体进行对抗。在此背景下,作战体系关键节点的分析具有重要的价值:它可以为我方在选择重点保护的作战要素时提供决策依据,也可以指导我方选择要重点打击的敌方目标。

随着网络科学的发展,基于复杂网络的作战体系关键节点分析方法得到了许多学者的研究。但这些方法中大多数均是基于网络拓扑结构,无法考虑网络的实际行为和节点、关系的异质性,甚至中心性概念的提出也是源自回答如何根据网络结构来衡量节点重要性。此外,作战体系中节点和关系具有异质性,这也导致了重要节点含义的多义性。

针对此问题,研究人员进行了一系列的探索研究。Cares等将实体分为侦察节点、决策节点、影响节点和目标节点。在此基础上,谭跃进等提出了基于作战环的武器装备体系网络化建模方法,为作战体系关键节点的分析提供了新思路。李国栋等认为作战环的数量和长度是体系作战能力的重要影响因素,在此基础上通过度量节点失效对体系作战能力的影响来评价节点的重要性。赵丹玲等基于构建的指标体系计算作战环的能力,并用最大作战环能力作为体系能力。进一步地,利用节点移除法来度量节点移除后对体系作战能力和作战环数量的影响来评价节点的重要性。梁家林等则在构建指标体系的基础上,用作战环里节点和关系的加权自信息量之和表示作战环的自信息量,并基于此计算针对一个具体目标的体系能力,最后通过线性加权的方式求得体系在面向多目标时的能力。刘鹏等基于指标体系,利用能力满足度计算体系面向某一任务时的作战能力,并用均匀分布法对节点在面向不同任务时的相对节点重要性作出判断。

这些方法在实际应用过程中均取得了良好的效果,但在计算过程中也存在如下问题:① 如何确定作战环长度的影响权重,如文献[9]认为路径更长的广义作战环更重要,而文献[8]认为作战环越长,完成作战活动所需的节点越多,可靠性也越低;② 如何制定战技指标体系及指标权重;③ 作战任务与作战环之间没有必然联系;④ 如何选用合适的能力满足度函数;⑤ 节点、关系能力如何综合成作战环能力及作战环能力如何综合成体系能力;⑥ 节点、关系指标数据获取,尤其是敌方作战体系指标数据获取问题;⑦ 分析方法不具有一般性。这些问题极大地增加了方法的复杂性和不可操作性,也降低了方法分析结果的可靠性。关键节点分析方法中“简单但不准确,准确却很复杂”的问题同样适用于作战体系。

基于此,本文利用功能图来描述作战体系在面向任务时网络的功能以仿真网络的实际行为,提出一种基于功能图的作战体系关键节点分析方法。最后结合算例,验证了本文方法的有效性。

1 功能图定义

作战体系用图=(,)表示,其中={,,…,}代表节点集合,={,,…,}代表边的集合,表示节点的个数,表示边的个数。

1.1 功能图的定义

本文将功能图定义为:作战体系在面向不同的任务时,作战系统以不同的先后顺序发挥作用、互相协作,进而组合成的链状、树状或网状结构。将功能图实例定义为:功能图在作战体系中的具体体现。

一个作战体系可以执行多项任务,具备多种功能,因此体系与功能图是一对多的关系。一个功能图在网络里可以有多种具体实现,因此功能图与功能图实例是一对多的关系。

1.2 功能图示例

作战环指为完成特定的作战任务,武器装备体系中侦察类、决策类、攻击类等武器装备实体与目标实体构成的闭合回路,如图1所示。其中,S为侦察节点、D为决策节点、I为攻击节点、T为目标节点。因此,作战环是武器装备体系与特定作战任务相关的一个功能图。

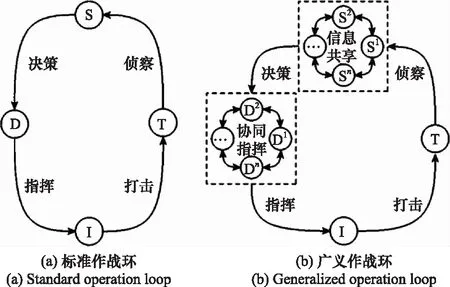
图1 作战环示意图Fig.1 Graph of the operation loop

图2是一个海上反击作战体系网络图。从图中可知,T->S1->D2->I1->T是一个功能图实例(作战环实例),T->S3->D1->I3->T是另一个功能图实例。

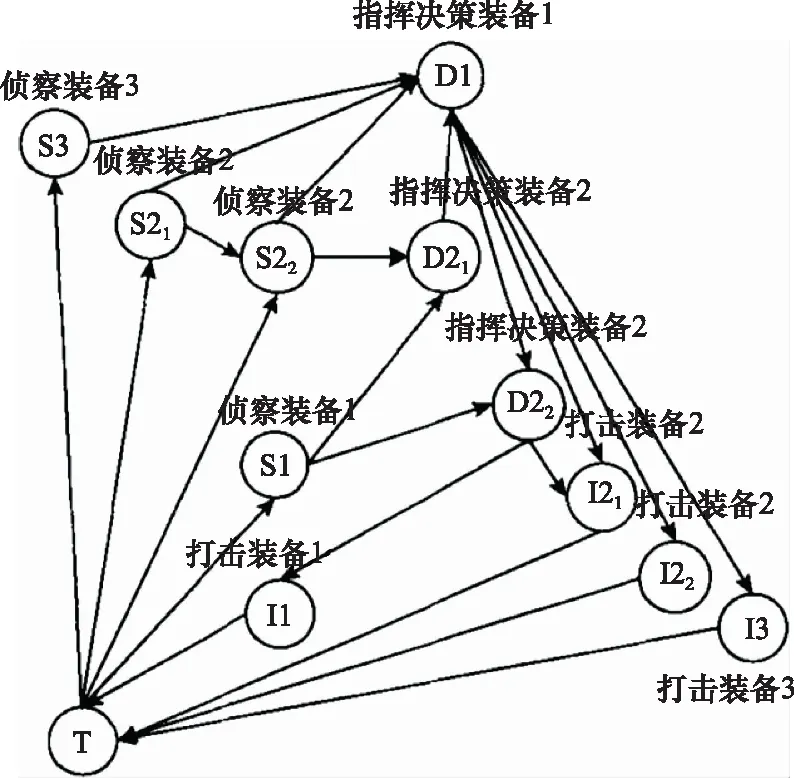
图2 海上反击作战体系Fig.2 Sea counterattack combat system

信息传输链指根据信息在作战网络中的传输方向、状态和效果产生过程,信息在收集、处理、使用和使其产生效果这4类用户之间的不含回路的传输路径。如图3所示,其中T是中继节点、C是收集节点、P是处理节点、U是使用节点、E是产生效果的节点。因此,信息传输链是作战网络中与信息处理相关的一个功能图。

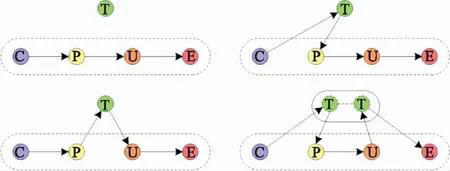
图3 信息传输链示意图Fig.3 Information transfermation chain

图4是一个军事通信网络示意图,从图中可知,C2->T2->P1->T3->T4->U2->T5->E1是一个功能图实例(信息传输链实例),C2->T2->P1->T3->T4->U2->T5->E2是另一个功能图实例。

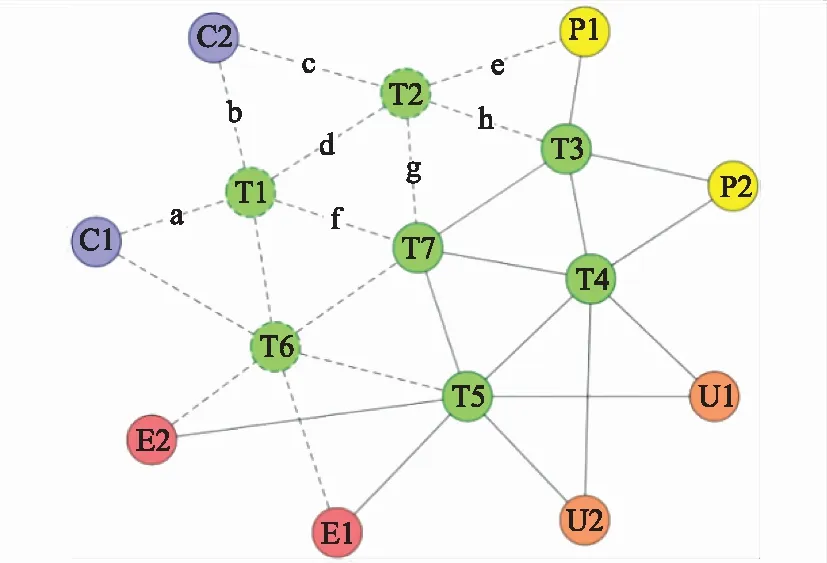
图4 一个军事通信网络示意图Fig.4 Graph of a military communication network

2 基于功能图的关键节点分析方法

基于功能图的关键节点分析方法可以看成通过限定能量或信息的传播方式,对现有基于网络拓扑关键节点分析方法的一种改进方法,而功能图则是一种从网络功能上对所分析网络的抽象。

本文选取分属4种不同类型关键节点分析方法里比较有代表性的5个方法,论述在不考虑作战节点重要性的前提下,如何用功能图对这些传统方法进行改进。

2.1 基于功能图的度中心性

度中心性认为节点的邻居越多其影响力越大。但在作战体系中,因为节点或关系具备不同的角色,因此不能直接用邻居节点数来衡量节点的重要性。

基于功能图的度中心性可以定义为与节点直接相连的属于功能图实例的边数。

分析图2所示多层作战体系节点对目标的打击能力时,应当选用“打击链路(影响节点指向目标节点)”作为功能图。因此,根据基于功能图的度中心性结果,侦察装备、指挥决策装备和目标节点的重要性为0,打击装备I1、I2、I2、I3重要性为1。

2.2 基于功能图的介数中心性

介数中心性用通过节点的最短路径数目度量节点的重要性,它假设信息通过最短路径传播。指标定义如下:

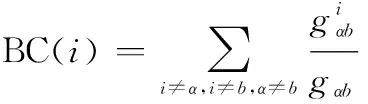
(1)

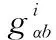
但针对如图2所示的多层作战体系,当采用基于最短路径的介数中心性进行关键节点分析时分析的过程和结果都与实际情况有所偏差。如从节点D2->I1->T是从节点D2到节点T的最短路径,但是从完成特定作战任务的角度而言却不具有现实意义,因为缺乏侦察节点的参与,且侦察节点的侦察范围必须覆盖到目标节点。

因此,可以将基于功能图的介数中心性指标定义如下:

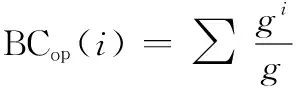
(2)

式中：表示功能图实例数；表示经过节点的功能图实例数。需要说明的是,针对不同的体系和功能图,基于功能图的中心性指标需要作出不同的调整。如针对图2所示的多层作战体系,选取作战环为其功能图时,基于介数中心性指标定义如下:

(3)

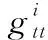
2.3 基于功能图的接近中心性

接近中心性通过计算节点与网络中其他所有节点的距离的平均值来度量节点的重要性。该指标可以反映出信息在网络中平均反应时间。指标定义如下:

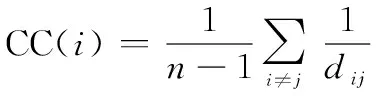
(4)

式中：表示节点到的最短路径长度。

基于功能图的接近中心性指标可以定义为节点通过功能图实例发挥作用的平均性能或效能指标。指标定义如下:

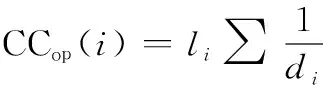
(5)

式中：表示包含节点的功能图实例的性能、效能指标,如时间、距离、效率等;表示为对比不同类别节点而设置的归一化系数。特别地,针对图2所示的多层作战体系,选取作战环为功能图,其接近中心性指标定义如下:

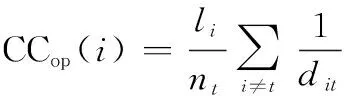
(6)

式中：表示隶属功能图实例的从节点到目标的最短路径长度;表示目标节点数目;表示为对比不同类别节点而设置的归一化系数。针对标准作战环,侦察节点的=3,决策节点的=2,影响节点的=1。广义作战环可近似参考标准作战环取值。此时,基于功能图的接近中心性计算结果可以反映节点对所有目标有效发挥战力的能力。

2.4 基于功能图的PageRank算法

PageRank算法最初应用于谷歌搜索引擎,它认为网页节点的重要性取决于指向该网页节点的数量和质量。

基于功能图的PageRank算法可以定义为:节点的重要性取决于指向节点的属于功能图实例的节点的数量和质量。如针对作战体系,应用基于功能图的PageRank算法分析侦察节点在协同过程中的贡献时,可以将“侦察协同链(侦察节点指向侦察节点)”作为功能图。此时,该方法在计算过程中不会考虑目标节点指向侦察节点。

2.5 基于功能图的节点移除和收缩的排序方法

节点的移除或收缩方法与系统科学中确定系统核心的思路相符。节点移除或收缩方法的核心思想是节点(集)被删除后对网络结构与功能的破坏。因此,基于节点移除或收缩的排序方法关键在于选取什么指标来度量网络的结构与功能。常用的度量指标包括连通分支数、网络连通性、不相交路径、残余接近中心性、生成树的数量、网络邻接矩阵最大特征值、凝聚度等。

基于功能图的节点移除和收缩的排序方法核心是如何用功能图衡量网络的功能。因功能图是网络功能在一定程度上的抽象,因此基于功能图的节点移除和收缩方法与基于网络拓扑的节点移除和收缩方法相比具有自底而上的优势。针对图2所示的作战体系,选取作战环为其功能图,可以选取功能图实例的数量、不相交功能图实例数量、用功能图替代最短路径,用基于功能图的残余接近中心性等指标来度量作战体系的功能。特别地,基于功能图数量的节点移除法用节点移除时作战体系功能图实例数量(当考虑功能图长度影响时,用功能图实例的权重之和)减少的大小来度量节点的重要性。

3 案例分析

本文以图5所示某作战体系网络图为例,在原文献作战体系的基础上增加一个目标节点,并假定所有侦察节点都可以侦察到它,所有攻击节点都可以打击到它,分析该体系在执行某作战任务时节点的重要性,因此选取作战环为作战体系的功能图。图5中节点名称含义同图2。

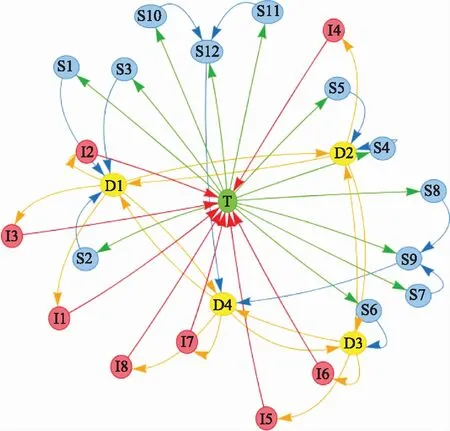
图5 一个作战体系网络图Fig.5 Graph of a combat system network

本文选用介数中心性、接近中心性、基于功能图的介数中心性、基于功能图的接近中心性、基于功能图数量的节点移除法来评价节点重要性。在不考虑节点和边作战性能的情况下,作战环数量(即功能图实例数量)是影响作战体系作战能力和效能的重要指标:作战环数量越多,体系的作战潜能越大,攻击敌方的方案越多,体系的抗毁性越强。因此,基于功能图数量的节点移除法计算结果可以有效地反映出节点的重要性,可以作为其他算法排序结果是否合理的判定依据之一。

为使计算结果与原文献计算结果更具有对比性,计算基于功能图的介数中心性和基于功能图数量的节点移除法时,同样也考虑功能图的长度影响,其影响方式与原文献相同。

(1) 表1可以看出:从相关系数和相对熵可知,相对介数中心性而言,基于功能图的介数中心性与基于功能图数量的节点移除法计算结果与原始文献排名结果更接近。

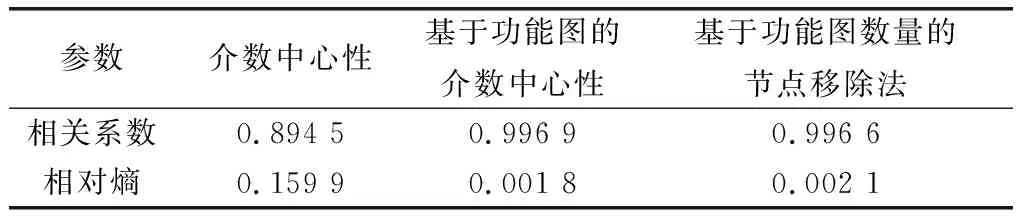
表1 与原始文献计算结果对比

(2) 从图6(a)、图6(b)、图6(c)、图6(d)可以看出:基于网络拓扑的中心性指标计算方法不能区分作战体系中网络节点的异质性。它们将侦察、决策、攻击、目标节点当作同类节点看待。但作战体系分析的是侦察、决策及影响节点对目标的威胁程度,所以目标节点不应在分析范围之内。基于功能图的中心性指标计算方法则对此进行了区分。

(3) 从图6(b)、图6(e)、图6(f)可以看出:基于功能图的介数中心性与基于功能图数量的节点移除法排名结果完全一致,说明基于功能图的介数中心性计算方法较好地识别出了节点之间的相对重要性。与原文献计算结果相比,它们均识别出了D1、D4、D2、D3、S9、I1、I2、I3、S7、S8、S10、S11的相对重要性。

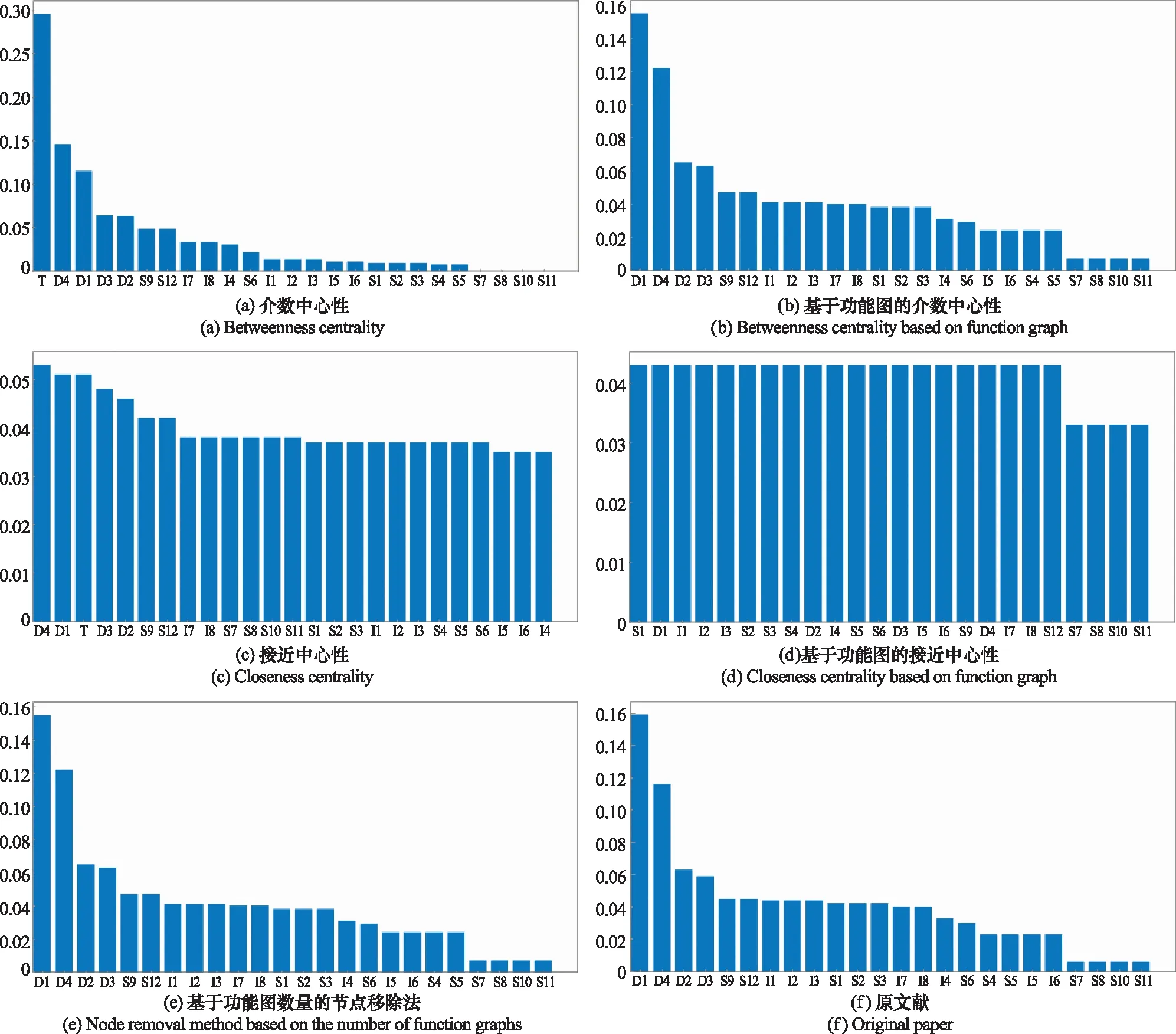
图6 计算结果对比分析Fig.6 Comparison analysis of calculation results

(4) 从图6(c)和图6(d)子图可以看出:基于功能图的接近中心性计算结果反映了除S7、S8、S10、S11节点外,其余节点到目标节点的最短功能图路径长度均相同,而S7、S8节点到目标节点必须要经过S9节点,S10、S11节点到目标节点必须经过S12节点的事实,节点排名越高,反映了节点到目标节点长度越短、节点影响目标节点的能力越强。相比接近中心性而言,基于功能图的接近中心性计算结果更具有可解释性。

4 结束语

本文针对现有作战体系分析方法“简单但不准确,准确却很复杂”的情况,结合基于网络拓扑的关键节点分析方法与基于作战环的关键节点分析方法优点的基础上,提出了基于功能图的复杂网络关键节点分析方法。本文方法主要做了以下改进:

(1) 本文以功能图描述作战体系的功能。同一个网络,可以针对作战体系所接受的任务,提出不同形式的功能图。通过限定能量或信息传播方式,对基于网络拓扑的关键节点分析方法进行改进,使计算结果更加精确。

(2) 本文所述方法可以从不同的业务角度分析节点的重要性。功能图考虑了节点和关系的异质性,因此可以分析基于网络拓扑的中心性指标计算方法无法分析的内容。如基于功能图的接近中心性具有分析节点有效发挥战力的能力。

(3) 本文所述方法可以一定程度上“统一”基于网络拓扑的关键节点分析方法。如分析作战体系,选取作战环为功能图时,针对介数中心性、流介数中心性和Katz中心性,最短路径和非最短路径可以用功能图中的标准作战环和广义作战环来限定。

(4) 本文所述方法相比基于作战环的关键节点分析方法,分析过程中不要求分析人员具有很强的专业背景知识,经验因素占比更小、分析结果更加稳定、方法更具有一般性。此外,本文所述方法也可以较好地应用于缺乏指标数据的作战体系,如敌方作战体系。

本文只针对少数几个中心性指标的基于功能图的改进方法做了验证。因此,在作战体系上进行更多基于功能图方法的验证是下一步工作重点。此外,不同的网络,不同的分析角度需要结合一定的专业背景知识选取不同的功能图及不同的关键节点分析方法,这在一定程度上增加了分析方法的复杂性。这个过程的简化是下一步的研究方向。