产能限制下单向替代产品供应链生产、订货与定价研究

罗治洪, 洪玉婷

(昆明理工大学 管理与经济学院,云南 昆明 650093)

0 引言

供应链上制造企业受资源(如产能)限制和产线品种频繁切换造成资源浪费等因素的影响，提供功能类似的替代产品成为满足需求的一种可选行为。替代分为单向和双向替代。本文仅考虑单向替代，当较高质量产品有剩余而较低质量产品缺货时，通过按低质量产品价格销售高质量产品的方式来满足需求，反之不行[1,2]。单向替代作为提升顾客服务水平、提高销售收益的策略已引起业界的重视。如，钢铁生产希望品种越少越好，但这与需求多样化相矛盾，则用较高钢级产品来替代满足较低钢级需求[3]。响应性定价是一种采用定价控制市场需求的策略，如一些手机企业在饥饿营销中就采用该策略定价。Zara等服装企业因受库存积压或缺货困扰而采用响应性定价[4]，研究表明响应性定价是销售企业应对需求不确定的一种有效机制[5～7]。另外，下游向制造商提供市场需求信息和承诺不使用替代性交货的那部分产品满足较高质量产品需求成为一种有限合作，相较于信息完全不对称，拥有信息优势将降低过少或过量生产的风险从而使企业获益。基于上述背景，本文研究两种可单向替代产品在信息不完全对称情景下的生产、订购及定价的供应链决策问题。

供应链单一产品定价问题研究较多，而可替代品定价问题逐渐引起了学术界的关注。Karakul等[8,9]在需求服从连续分布的情形下，研究订购与定价受被改进产品单向替代的影响程度。Nazari和Seifbarghy[10]考虑随机线性需求下两个制造商通过双渠道销售两种可替代产品，分析纳什均衡和Stackelberg博弈下的定价策略，得出提高品牌忠诚度有利于制造商和零售商利润增加的结论。过去关于可替代产品的供应链定价研究主要考虑消费者选择的替代，而企业进行的“主动式”替代下的定价研究非常少见。

针对信息不完全对称下定价问题，谭德庆[11]等讨论了市场中地位相等的两个寡头企业对具有一定替代性的两种产品定价问题，考虑双方对产品成本不完全对称信息建立了静态贝叶斯博弈的Bertrand模型；Lim等[12]研究生产商对零部件的质量具有不完全信息下的采购合同优化问题。朱琳等[13]在产出随机下建立了供需双方之间的三种博弈模型(生产商主导，销售商主导和纳什博弈)并分析了最优生产与订购决策；王丽梅等[14]在产需不确定下制定供应链协调的最优订购与退货价格决策。这些文献主要以质量或成本、供应链上下游产量与需求具有不完全对称信息的前提下进行了研究。

梁云等[15]研究闭环供应链环境下最优定价与利润受制造商产能限制和废旧产品回收量的影响。Huang等[16]发现需求随机和产能有限时，制造商通过批发价回购和扩张产能两种策略使其利润最大化。现有关于制造商产能限制的供应链优化研究，通常考虑采用扩张产能或供应链回购等契约来解决，未考虑产品替代的方式。

与已有文献不同，本文考虑制造商受产能限制、产品单向可替代、下游以市场需求信息和非投机性的承诺换取制造商产量信息的情景下研究供应链上的生产、订货与定价问题。首先建立一个制造商和一个零售商的单周期博弈模型，其次理论分析制造商和零售商的最优决策及其条件，最后数值分析探讨价格敏感系数、制造商产能以及潜在市场需求变化对制造商生产和零售商订货决策的影响。

1 问题描述

考虑具有产能限制的制造商和零售商组成的两层供应链系统，制造商同时生产并向零售商销售1和2两种类似的产品，1为较高档产品，2为较低档产品。当满足产品1有剩余而2缺货时，制造商才会用产品1来满足零售商对2的需求，同时零售商承诺替代的这部分产品只能以产品2的价格满足市场需求。产品的潜在市场需求服从某一连续分布，为零售商的私人信息，为降低供需不匹配的风险，制造商共享两种产品的产量信息和单向替代策略来激励零售商实现私有信息的共享和有限合作。

在供需双方信息不完全对称的情形下，制造商不掌握零售商的定价方式，零售商不知道制造商的成本结构和产能限额。制造商先根据由零售商处获得的潜在市场需求信息确定生产量，零售商根据制造商制定的批发价格和产量在销售季节来临之前确定两种产品订货量，最后零售商根据市场需求和制造商的实际交货量采用响应性定价确定产品的零售价格，即零售商收到货物后根据确定的需求信息决定最终投放到市场上的供应量。产品价格受到市场上产品供应量的影响，因而决定了产品的零售价格[7]。根据决策过程，建立制造商为主导的Stackelberg博弈模型。

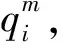
不失一般性，产品1的单位生产成本、批发价格、零售价格均大于产品2，即c1>c2，e1>e2，w1>w2，p1>p2。假定p1-w1>p2-w2表明产品1比产品2高档。当产品1替代产品2时，制造商按照产品2的批发价格进行交货，此过程会产生替代损失，为了简化问题，只考虑价格变化产生的损失(即w1-w2)，未销售的两种产品的残值为零。产能足够时制造商一般不会考虑替代交货，因此假定S<(e1+e2)H。

2 模型的建立与求解

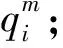
2.1 零售商响应性定价决策

根据逆向递归法，先求解零售商以收益最大化的定价问题。零售商在已知制造商的产量信息下做出订货决策，订货总量不会超出制造商总产量，尽管制造商可以替代交货，但本文不考虑零售商对市场的替代行为，因此，实际交货量为订货量。令ΩR表示零售商的收益，则零售商定价问题为:

(2)

式中pi=αi-biDi。最优定价如性质1所示。

性质1产品1和2的最优定价为:

(3)

(4)

零售商的最优收益为:

(5)

证明式(2)松弛得到Lagrange函数为:

LΩR=(a1-b1D1)D1+(a2-b2D2)D2+λ1D1+

(6)

(7)

(8)

不难发现LΩR关于D1和D2的Hessian矩阵负定，由(7)、(8)得最优D1和D2。分为五种情况：

归纳上述2)～5)，可得(3)～(5)。证毕

上述性质1表明，当产品1和2的生产量较大时，零售商对两种产品的市场定价为确定值p1=a1/2和p2=a2/2，不随产品实际交货量而改变；当生产量较小时，零售商根据实际交货量采用市场出清价格。

2.2 零售商订货决策

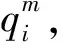
(9)

零售商的订货决策需满足约束条件:

(10)

约束(10)松弛得到Lagrange函数:

(11)

(12)

(13)

零售商的最优订货决策如性质2所示。

性质2零售商最优订货决策分为如下情形：

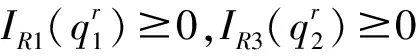
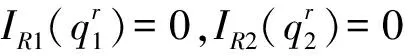
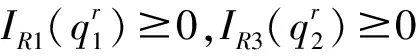
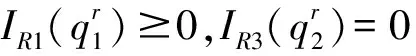
证明分析约束条件(10)和制造商的交货策略，当发生替代时，可能的情形为：产品1的剩余量刚好等于产品2的缺货量；产品1的剩余量大于产品2的缺货量。当不发生替代时，可能的情形为：产品1和2的订货量刚好分别等于各自生产量；产品1和2中一种产品有剩余另一种无剩余。分别对应五种情形：

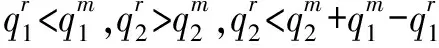
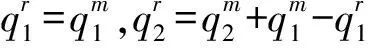
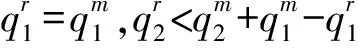
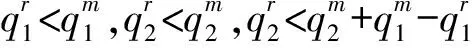
综上，可得结论。证毕

性质2的分析过程也说明了零售商最优订货决策的可能情形，当潜在市场需求分布具体化时，选择使目标值大的最优订货即可。

2.3 制造商生产量决策

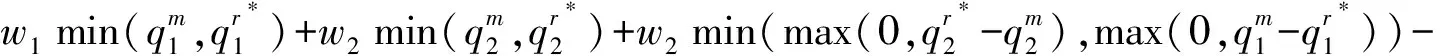
(14)

(15)

松弛产能约束并建立Lagrange函数:

(16)

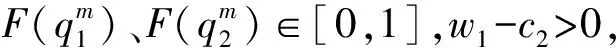
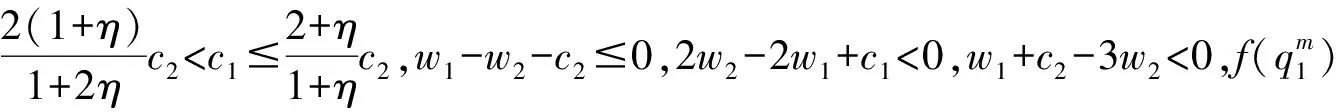
上述过程说明了不同条件下的最优解计算。零售商承诺被替代交货的那部分产品只能用于产品2的销售，零售商销售产品1的单位利润比2高，因此不会投机性地减少产品1的订货，但可能会减少产品2订货。从理论分析可以看出，当产品1成本相对较低时(即上述前两种情况)，全部生产产品1，但是当产品1成本相对较高时，难以容忍替代损失的增加，产品2就可能会生产。

3 算例分析

以文献[15,17]为参考，两种产品潜在市场需求服从均匀分布U(A,B)，A=300，B=400，其余参数为：c1=25，c2=15，e1=2，e2=1，b1=0.9，b2=0.6，η=80%。本文不关注产能有剩余的情形，计算出产能临界点S=1363.6，将产能限制值取为1000。下面分析价格敏感系数、产能及潜在市场需求的期望和方差对产量、订货量及利润的影响。

1)价格敏感系数的影响

表1 b1对产量、订货量和利润的影响

表2 b2对产量、订货量和利润的影响

2)产能的影响

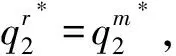
表3 S对产品产量、订货量和利润的影响

3)潜在市场需求期望和方差的影响

表4 E(αi)的期望对产量、订货量和利润的影响

表5 D(αi)对生产量、订货量和利润的影响

综上，制造商产能、潜在需求及其方差、替代品的价格敏感系数在一定范围内增大有利于供应链系统及各成员利润增加，而被替代产品的价格敏感系数增大可能会导致供应链及制造商利润下降。

4 结论

本文探讨了供需双方信息不完全对称下，具有单向可替代性两种产品的产量和订购量及响应性定价的供应链决策问题。研究结果表明，价格敏感系数、潜在市场需求的期望和方差这些企业不可控因素变大时，零售商更趋向于选择订货量等于或小于制造商的生产量(不替代)的方式进行订货，而产能的提高使零售商接受替代产品的机会变小。替代性交货作为一种制造商为保留甚至提高市场占有的策略值得进一步深入研究，如，如何确保下游企业获得的那部分替代产品1确实用来满足2的需求？如果允许这种情况发生，零售商具有投机动机的前提下如何进行供应链优化决策？等等。