考虑延期成本承诺交货时间与产能扩张决策

谢祥添

（广东金融学院 科技金融重点实验室，广东 广州 510521）

1 引言

Stalk J G[1]提出时间将成为企业获得竞争优势的下一个资源。当前，时间已经与价格一样成为企业在市场竞争中获得优势的因素之一。So K C 等[2]认为企业以时间作为武器吸引客户有三种策略：（1）快速服务；（2）提前预约；（3）承诺交货时间。其中，订单式生产企业多采用第三种策略。相对另外两种策略，承诺一个统一的交货时间较为有效[3]。由于受内（如设备故障、人员流动等）外（如需求、原材料供应等）多种不确定因素的影响，企业难以实现100%按时交货[4]。为此，部分企业承诺若不能按时交货，则给予一定的赔偿。如EMS承诺因自身原因造成邮件时限延误的，可退还已收取的邮件资费。Slotnick S A等[5]提及飞机零部件供应商延期交货赔偿几百万美元。Ho T H 等[6]提出企业既能承诺一个较短的交货时间，又能保证交货时间的可靠性（即按时交货的概率，部分文献称之为服务水平），就能吸引对时间敏感的客户。那么，承诺多长的交货时间一方面能吸引客户，另一方面又不会导致延期交货频繁从而付出过多的延期成本？

因此，考虑延期成本与承诺交货时间的决策成为学者研究的焦点。较早对此研究的是Seidmann A等[7]，他们建立以时间总成本（包括交货时间成本、延期成本和提前交货成本）为目标函数，以承诺交货时间为决策变量的模型，证明了实际交货时间服从任意随机分布，存在最优承诺交货时间使目标函数最小化。随后，Grout J R 等[4]考虑延期成本和提前交货成本研究供应链交货时间问题，证明了100%按时交货是奢望；同时，他们还提出了实际交货时间分别服从均匀分布、指数分布和三角分布时交货时间成本最小化的条件。Hill A V 等[8]考虑延期成本，建立了以企业利润为目标函数，以承诺交货时间为决策变量的模型，得到了最优承诺交货时间数学表达式。该模型权衡了承诺交货时间和延期成本的关系。最近部分学者研究了多阶段生产的交货时间问题。如Atan Z 等[9]研究了订单驱动的多阶段装配生产系统交货时间决策问题，他们建立了以订单总成本（包括提前交货成本和延期成本）为目标函数，以每一阶段交货时间为决策变量的模型，推导出多阶段库存成本和延期成本递推方程，提出了一个求解多阶段交货时间的迭代启发式算法。Jansen S 等[10]研究了由多个并行子组件阶段和一个最终组装阶段组成的按订单生产的交货时间问题，他们考虑每个阶段都有一个随机的提前期，以及最终装配阶段延期产生罚款，建立以每个阶段交货时间为决策变量，以总期望成本最小化为目标函数的模型，通过对模型的分析，得出了最优交货时间满足报童过程。在我国，周颖[11]基于客户价值，考虑延期成本，建立了客户选择行为的承诺交货时间决策模型，证明了模型存在最优承诺交货时间使企业利润达到最大化和最优承诺交货时间长于顾客期望的交货时间。倪卫涛等[12]考虑提前交货产生仓储成本和延期交货支付罚金，建立以订单生产式企业单品收益为目标函数，以承诺交货时间为决策变量的模型，证明了模型存在最优承诺交货时间使企业边际收益达到最大化。

以上主要从时间成本研究交货时间的决策。然而，在需求一定的前提下，交货时间随着产能的增加而减少，随着产能的减少而增加。所以有部分学者研究了承诺交货时间和产能联合决策问题。如，Nguyen T H 等[13]提出企业不仅要考虑客户如何对交货时间保证作出反应，还要考虑其是否有足够的产能履行承诺。因此，他们研究了企业利润与承诺交货时间和产能的关系，得出了需求时间变化下最优的承诺交货时间和产能。谢祥添等[14]考虑需求具有数量和时间两方面的不确定性，采用作业成本法建立以承诺交货时间和产能为决策变量，以期望利润为目标函数的模型，给出了最优承诺交货时间和最优产能满足的方程组，该研究表明结合生产过程和承诺交货时间可靠性有助于提高产能的利用率和交货时间的准确性。Albana A S 等[15]考虑运营成本是时间敏感，分别建立了交货时间决策模型、交货时间与价格决策模型和交货时间、价格和产能决策模型，给出了各个模型的最优策略。以上文献通过产能和交货时间联合决策得到了可靠性较高的交货时间，因而忽略了延期成本，但是随着时间竞争的加剧，客户对准时交货的重视，企业纷纷提出若不能按时交货，承诺支付一定的赔偿。因此，本文考虑延期交货尾概率分布为指数分布，构建了包含延期成本的承诺交货时间和产能决策模型。

本文的贡献在于考虑延期成本，以及产能与交货时间的关系，建立以承诺交货时间和产能为决策变量的模型，得到了联合最优的承诺交货时间和产能扩张。以此分析得出企业利润随着承诺交货时间或产能扩张的增加先增加后减少，两者相比，企业利润受承诺交货时间影响更大。

2 模型的建立

2.1 模型参数及说明

r=单位收入，单价减去单位成本（除延期成本和产能成本外）；

c1=延期单位成本；

u=当前产能，当前生产系统可以生产的产品数；

z=产能扩张，企业通过加班或增加临时工等方式增加生产系统的产能；

c2=当前产能单位成本；

c3=产能扩张单位成本；

l=承诺交货时间；

L=实际交货时间；

P{L≤l}=实际交货时间小于等于承诺交货时间的概率。

2.2 需求函数

考虑客户倾向于较短的交货时间，建立承诺交货时间需求函数：

式中，a 为b=0（需求与承诺交货时间不敏感）时的需求（部分文献称之为潜在需求），b为需求承诺交货时间敏感系数（b≥0）。承诺交货时间需求函数有线性的，如 Wu Z 等[16]、Pekgun P 等[17]研究文献的函数；也有非线性的，如 Hill A V 等[18]、Mallick R K 等[19]研究文献的函数。

2.3 延期成本函数

众多学者，如Kelton W D等[20]和Bratley P等[21]均指出实际交货时间小于等于承诺交货时间的尾概率分布为指数分布：

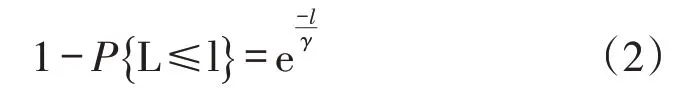
其中，γ为实际交货时间均值。因为在需求一定的前提下，交货时间受产能的影响：产能越大交货时间越短，产能越小交货时间越长。所以产能与实际交货时间均值γ 有减函数的关系[8]。在减函数关系中，我们假设它们成反比例的关系，构建实际交货时间均值γ关于产能的函数：

其中，θ为实际交货时间均值γ与产能关系系数（θ＞0），其值可以通过统计分析（如回归分析）确定。

因为延期交货概率P{L＞l}=1-P{L≤l}，所以结合式（2）和式（3），可得关于产能和承诺交货时间的延期交货概率函数：

设u=50，θ=45。作产能扩张z 分别为 0，15 和 50时的延期交货概率，如图1 所示。从图1 可知，随着产能扩张的增大，延期交货概率减小。

图1 产能扩张与延期交货概率

根据式（1）和式（4），可得延期成本函数：

2.4 模型构建

考虑延期成本，建立以企业利润为目标函数，以承诺交货时间和产能扩张为决策变量的模型。

其中，第一项为收入；第二项为延期成本；第三项为产能成本。

3 模型分析

3.1 承诺交货时间为决策变量

命题1 若仅以承诺交货时间为决策变量，模型存在最优承诺交货时间，它的表达式为：

其中，LambertW(x)为欧米加函数或乘数对数[22]。

证明：式（6）对l 求一阶偏导数，令其为零整理得：

设 t1=c1a(u+z)/θ+c1b，t2=c1b(u+z)/θ，t3=(u+z)/θ 和x=-lt3=-l(u+z)/θ，那么式（8）变换为：

又设y=t1+xt2/t3,，这时式（9）变换为：

以yt3/t2作为未知数，求式(11)可得：

这时把y=t1+xt2/t3和x=-lt3代入式（12）化简得：

再把 t1=c1a(u+z)/θ+c1b，t2=c1b(u+z)/θ 和 t3=(u+z)/θ代入式（13）求解l，得：

又因为式（6）对l求二阶偏导数有：

所以，式（6）关于l 存在最大值，最优解为式（6）对l求一阶偏导数为零的解，即式（14）。因此，命题1成立。

命题1结论：若不允许延期交货（令c1=∞），这时有l*=a/b+θ/(u+z)，这表明最优承诺交货时间随着潜在需求a的增加而增加，随着需求承诺交货时间敏感系数b和产能扩张z的增加而减少。所以企业在需大于供的市场中，承诺交货时间较长；在需求时间越敏感的市场中，承诺的交货时间越短。承诺交货时间与产能有减函数的关系。

3.2 产能为决策变量

命题2若仅以产能扩张为决策变量，模型存在最优产能扩张，它的表达式为：

证明：式（6）对z求一阶偏导数为零：

求解式（16）可得z的表达式：

又因为式（6）对z求二阶偏导数有：

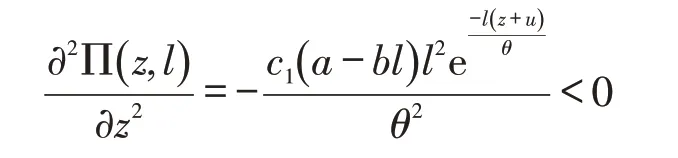
所以命题2成立。

命题2结论：由式（15）得：z*=-u-θln(c3θ)/l+θln[c1l(a-bl)]/l。这表明最优产能扩张随着当前产能u，产能扩张单位成本c3和需求承诺交货时间敏感系数b的增加而减少，随着延期单位成本c1和潜在需求a增加而增加。同时易知，系统处于最优状态为产能扩张为零时，即当前产能满足：u=-θln(c3θ)/l+θln[c1l(a-bl)]/l。

3.3 承诺交货时间和产能为决策变量

（1）交替决策。企业在承诺交货时间和产能决策前，一般存在着产能，这时产能扩张为0，设z(0)=0。在z(0)前提下，企业可以根据式（7）确定最优承诺交货时间，设为l(0)*，这时企业得到第一次决策的最优利润。接着，企业在l(0)*前提下，根据式（15）可得最优产能扩张，设为z(0)*，这时企业得到了第二次决策的最优利润，如此反复。

当然，企业也可以以当前的承诺交货时间作为初始承诺交货时间，然后在初始承诺交货时间条件下确定最优产能扩张。余下的决策过程与上述一致，略。

（2）同时决策

引理1 若(l0,z0)为式（6）的极值点，那它满足以下方程组：

证明：设(l0,z0)为式（6）的极值点，把它代入式（6）分别对l 和z 求一阶偏导数为零的方程组，可得式（18），所以引理1成立。

命题3 若存在极值点(l0,z0)使得式（19）成立，那么该极值点为极大值点。

根据引理1可得极值点(l0,z0)，把极值点(l0,z0)分别代入A，B和C。根据极值点判断公式有：

由式（19）可得Δ ＞0，又因为A＜0，所以命题3成立。

命题3结论：模型不一定存在最优的承诺交货时间和产能扩张；若存在，那么对所有有实际意义极大值点的函数值和边界点(l*z=0,0)（把z=0代入式（7）可得l*z=0）的函数值进行相互比较，其中最大者就是模型的最优值，其对应的点就是最优的承诺交货时间和产能扩张。

4 数值实例

某衣服生产企业，其产品P 运营过程为：企业在网站发布产品P的信息（包括价格、交货时间、定制流程等），客户通过网站定制，企业根据客户要求生产，生产完毕后交付。产品P采用网上定制式生产，出现了延期交货频繁的问题，因此需要确定合适的承诺交货时间。

产品P根据历史数据统计分析可知：其承诺交货时间的尾概率分布近似服从指数分布，实际交货时间均值与产能成反比例关系，关系系数为45，每天出售 1 000-10l 件，售价为 50 元/件，生产成本为 20 元/件，延期成本为10 元/件，产能为50 件/天，产能成本为10 元/件，通过加班、增加工人等方法增加产能的成本为12元/件。（1）求经过3次产能扩张（6次交替决策）后产品P最优的承诺交货时间和产能；（2）求产品P最优的承诺交货时间和产能。

依题意有 r=50-20=30 元/件，c1=10 元/件，c2=10元/件，c3=12 元/件，u=50 件/天，z(0)=0 件/天，θ=45，a=1 000件/天，b=10。

（1）经过3次产能扩张后产品P最优的承诺交货时间和产能

第一次决策：把 z(0)=0 件/天，r=30 元/件，c1=10 元/件，u=50 件/天，θ=45，a=1 000 件/天和 b=10 代入式（7）得：

这时产品P的最优利润为：2.826 4万元/天。

第二次决策：把 l(0)*=3.232 天，c1=10 元/件，c3=12元/件，u=50件/天，θ=45，a=1 000件/天和b=10代入式（15）得：

这时产品P 的最优利润为：2.828 5 万元/天。余下决策过程见表1。

所以，经过3次产能扩张后，产品P的最优承诺交货时间为2.813 670 915天，最优产能为62.769 405 20件/天，最优利润为2.831 1万元/天。

（2）产品P最优的承诺交货时间和产能

把r=30元/件，c1=10元/件，c3=12元/件，u=50件/天，θ=45，a=1 000件/天，b=10代入式（18）得：

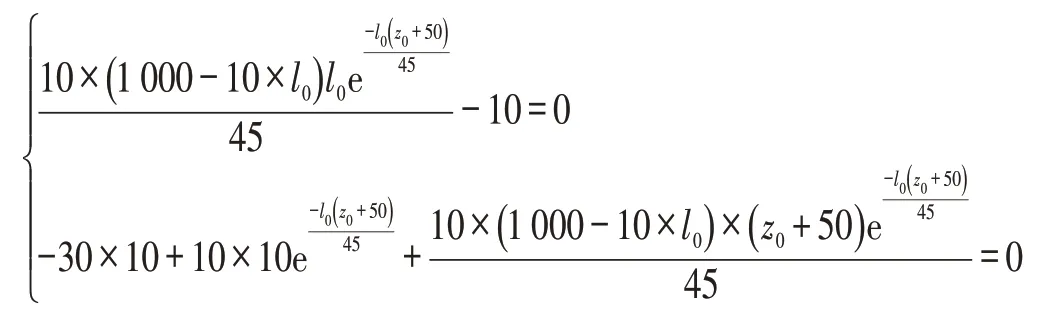
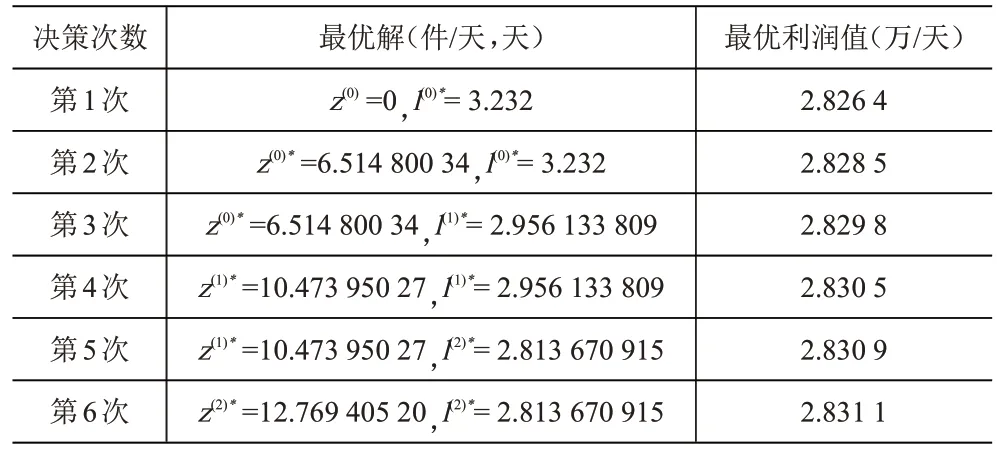
表1 最优承诺交货时间和产能决策

解上式得有实际意义的点为：{l0=2.647 000 263,z0=15.712 771 2}。把{l0=2.647 000 263,z0=15.71 2 771 2}代入式（19）有2.89×108＞0。所以{l0=2.647 000 263，z0=15.712 771 2}为极大值点，这时它对应的函数值为2.831 3万。因为{l0=2.647 000 263,z0=15.712 771 2}极大值点对应的值2.831 3大于边界点{l*z=0=3.232,z=0}对应的值2.826 4。所以，产品P的最优承诺交货时间为2.647 000 263 天，最优产能为 65.712 771 2 件/天，最优利润为2.831 3万元/天。

为了进一步弄清利润和承诺交货时间与产能扩张的关系，令 r=30 元/件，c1=10 元/件，c2=10 元/件，c3=12元/件，u=50件/天，θ=45，a=1 000件/天，b=10。

首先，把上述r=30 元/件等代入式（6）作图，如图2 所示。从图 2 可知，随着 l 和 z 的增加，Π(z,l)是先增加后减少的曲面，这表明企业存在最大利润。

其次，把上述r=30元/件等，以及l0=2.647 000 263天代入式（6）作图，如图3所示。从图3可知，随着z的增加，Π(z,l)先增加后减少，当Z达到15.712 771 2 件/天时，企业的利润最大。这说明企业初始增加产能缩短了交货时间，使得需求增加得到的利润多于总成本（延期成本和产能成本）的增加，所以利润增加，当产能扩张超过最优值后，需求增加带来的利润小于总成本的增加，导致利润下降。

最后，把上述r=30元/件等，以及z0=15.712 771 2件/天代入式（6）作图，如图4所示。从图4可知，随着l的增加，Π(z,l)先快速增加后逐渐减少，当达到2.647 000 263天时，企业的利润最大。这说明企业初始承诺交货时间增加，延期成本节约比需求减少导致利润减少多，所以利润增加，当承诺交货时间超过最优值后，则反之。同时，相对于z，Π(z,l)受到l的影响更加显著。

图2 利润和承诺交货时间与产能扩张的关系

图3 利润和产能扩张的关系

5 结束语

在需求一定的前提下，交货时间主要受产能的影响，本文考虑延期成本以及产能与交货时间的关系，构建了延期成本函数，在此基础上建立了以承诺交货时间和产能为决策变量的模型。通过模型分析，得到了相互递推的承诺交货时间和产能扩张关系式，在此基础上，求解得到了最优的承诺交货时间和产能扩张值。

图4 利润和承诺交货时间的关系

模型不一定存在最优的承诺交货时间和产能扩张值，若存在则可以根据命题3求得；若不存在，结合企业关于承诺交货时间和产能的决策过程，采用交替决策方法可得适合企业自身情况的承诺交货时间和产能。

最后，本文研究的延期成本仅考虑了企业是否按时交货，如果企业不按时交货则需要支付罚金。实际上，延期成本还会与延期时间长度相关，这有待进一步研究。