基于Bagging集成CHAID决策树算法的神东矿区煤灰熔融温度预测

张 挺，李寒旭，张 晔，陈和荆

(安徽理工大学化学工程学院，安徽 淮南 232001)

我国是世界上最大的煤炭产出消费国[1]，煤炭是我国重要的能源和化工原料[2]。神府东胜矿区作为世界七大矿区之一，煤质精良，具有“三低一高”的特点[3]，即低灰、低硫、低磷、高发热量，在气化领域表现出较大的竞争力[4]。神东矿区的煤灰熔点大部分偏低，黏温特性波动性大且易于结渣[5]，使得神东煤在气化过程中会产生很多问题。对于煤气化技术来说，煤灰熔融性是决定煤炭气化排渣方式的一个重要因素，所以扩大煤种适用范围具有重要意义。气化炉操作温度亦受限于煤灰熔融温度及黏温特性，因此，通过预测煤灰熔融温度来指导企业生产有重大意义[6]。

通常认为，煤灰熔融温度与灰成分中SiO2、Al2O3、Fe2O3、TiO2、CaO、MgO、Na2O、K2O等组分含量密切相关，传统公式的预测误差相对来说较大，预测精准度不高。并且，混煤灰熔融温度不符合各煤种灰熔融温度的简单线性加权叠加[7]。关于预测煤灰熔融性，国内外学者已经在这方面做了很多研究，研究至今并未发现一个被大众认可且计算能力强的预测方法来预测煤的灰熔点和灰成分之间的关系。杨伏生等[8]基于GA-BP算法对气化配煤灰熔点进行预测，结果表明经过GA算法优化后的BP网络预测算法的预测精度高于BP网络算法，GA-BP预测值的MSE为308.098，MAPE为0.9948。王陆顺[9]在基于神经网络的混煤灰熔点研究中通过BP神经网络与经验公式对测试集进行预测结果进行对比发现，BP神经网络得到的最大绝对误差仅为69 ℃远小于经验公式得出的最大绝对误差 603 ℃。王春林等[10]在基于支持向量机与遗传算法的灰熔点预测的实验中发现，优化后的支持向量机模型实现了对单煤和混煤灰熔点较精确的预测，对于掺混2种煤灰熔点Tst<1500 ℃和掺混2种煤灰熔点Tst>1500 ℃的最大预测误差为3.39%，平均预测误差为1.49%。

然而，前人众多研究预测的煤样种类繁杂没有针对性，本文提出针对神东矿区煤，以神东矿区煤的主要氧化物成分为输入量，建立基于Bagging集成CHAID决策树算法的神东矿区煤灰熔融温度预测模型，以便为神东矿区煤的利用提供指导。

1 集成CHAID决策树算法

1.1 CHAID决策树

CHAID(Chi-Square Automatic Interaction Detector)决策树算法又称卡方自动交互检测算法，主要特点是利用卡方检测判断属性优先级[11]。CHAID决策树多应用于一个因变量多个自变量的分类问题，对于一些变量较多，且分类较复杂的情形，CHAID决策树更加有效。CHAID决策树多运用于一个单因变量或多自变量的时长分析问题，但针对与一些变数较多，而且市场分析比较繁琐的情况，CHAID决策树比较合理。由于CHAID算法拥有受解析变量的限制而影响范围极小、不受解析变量之间的多重共线性影响以及分析结论清晰直接等优势，因此往往被市场调查企业作为市场的细分研究工具[12]，本文将CHAID算法应用于煤灰熔融温度的预测中是一次创新的举动。

CHAID决策树的主要思想为根据数据确定因变量和自变量，以卡方值等统计量为分支准则，在与设定的合并水平相比较的过程中通过不断合并、拆分因变量和自变量进行煤灰预测，直到满足树停止生长的条件。卡方值的计算公式如表1和式(1)、式(2)所示。

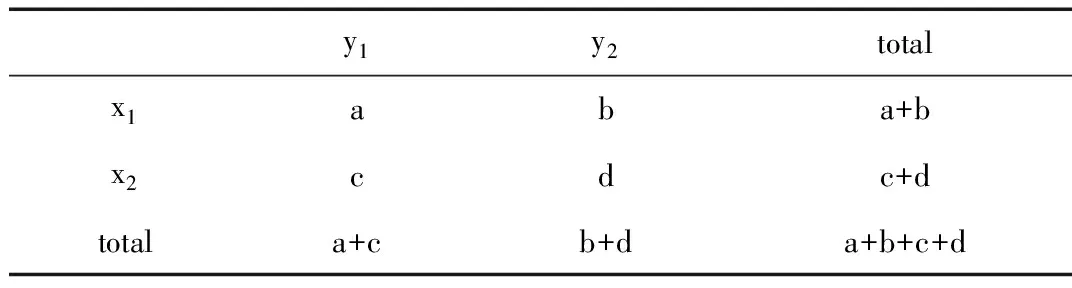
表1 卡方值计算公式所用的独立性检验事件关系Table 1 The independence test event relationship used in the cardinality formula

(1)

n=a+b+c+d

(2)

CHAID决策树的求解步骤如下：

(1)初始化。输入训练集数据S，训练集数据属性集合F，设CHAID决策树函数为DT(S，F)。

(2)if(样本S全部属于同一个类别C)

创建一个叶节点，并标记类标号为C；

return；

else

计算属性集F中目标属性与其他每一个属性的卡方值，取卡方值最大的属性；

创建结点，取属性A为该结点的决策属性；

for(结点属性A的每个可能的取值V)

为该结点添加一个新的分支，假设Sv为属性A取值为V的样本子集；

if(样本Sv全部属于同一个类别C)

为该分支添加一个叶结点，并标记类标号为C；

else

递归调用DT(Sv，F-{A})，为该分支创建子树；

end if

end for

end if

(3)输出CHAID决策树。

1.2 Bagging集成算法

决策树属于不稳定分类器[13]，为了优化CHAID决策树的预测结果，本文采用了集成学习算法进行优化，集成学习是通过某种方法整合数个基学习器提高整体模型的学习性能以完成任务，在机器学习分类任务中，常见的集成学习方法主要有串行和并行，普遍在用的集成方法有Boosting、Bagging等[14]，由于在测试过程中Boosting集成算法中的模型容易过拟合，为了使数据泛化更稳定，本文采用的是一种装袋法(Bagging)，即将CHAID决策树作为集成学习的分类器，采用投票机制，把分类器评估的概率在全部基分类器上求出其平均值以得出概率最高的预测温度，聚合不同的分类器进行灰熔融温度预测。常用的集成方式是训练一组单个的决策树分类器并通过投票机制得到最终预测结果[15]。集成学习模型可以集成同类基学习器和不同类基学习器，本文设计的集成方法为采取煤样的灰成分数据为训练集，在每轮学习的过程中有放回抽样从训练集中选取煤样灰成分数据，分别对基分类器进行训练，且采用并行的集成方法实现最终的灰熔融温度预测，并行的集成结构见图1所示。

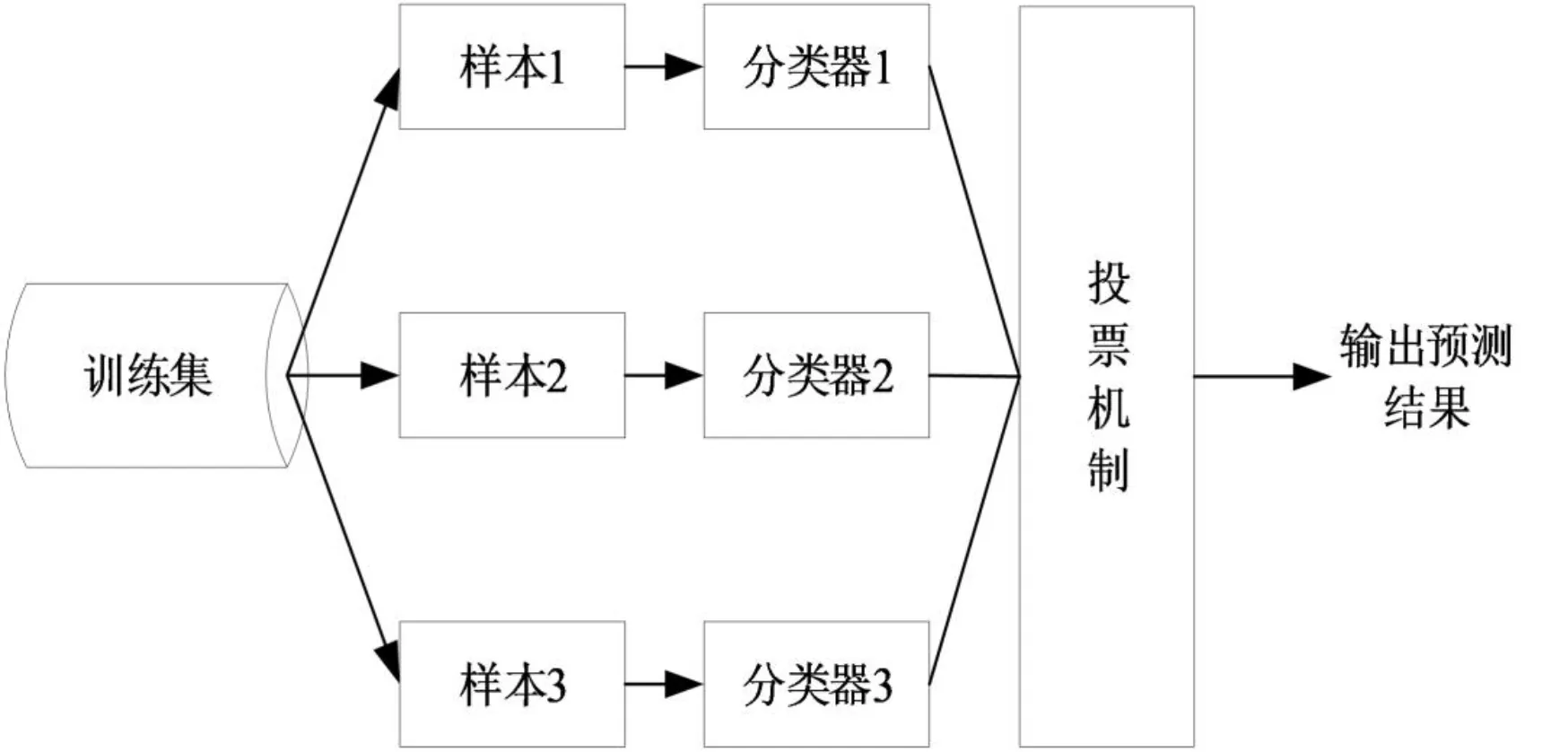
图1 Bagging集成基本结构Fig.1 Basic structure of Bagging integration

Bagging算法的伪代码[16]可表述如下：

input：TS D={(a1，b1)，(a2，b2)，(a3，b3)， …，(an，bn)}；

basic learning classifier C；

number of training M.

process：

for m=1 to M； //迭代次数M

Dm=Bootstrap(D)；

//使用训练集TS进行m次采样

Gm=C(Dm)；

//采样集Dm训练第m个分类器

end for

//TS结果

2 神东煤灰熔融温度Bagging集成CHAID算法模型

研究目的在于根据神东矿区煤灰的成分预测灰熔点，即建立以灰成分SiO2、Al2O3、Fe2O3、MgO、CaO、Na2O、K2O、TiO2为输入量，灰的软化温度(ST)和流动温度(FT)为输出量的集成CHAID算法预测模型。因此，需分析煤灰成分中各组分的含量以及各组分与煤灰熔融温度之间的相关性，对算法预测模型进行训练和检验。

2.1 煤灰的制备与分析

煤种数据来源于安徽理工大学灰化学实验室测定的神东矿区煤种数据以及前人的研究数据。

采用灰锥法测定灰熔点，按照GB 474-2008制备煤样，将煤样放置在马弗炉中按照GB 212-77在815 ℃下制成煤灰样。根据国标GB/T 219-2008规定的煤灰熔融性测定方法，将煤灰制成三角锥体，把灰锥放置在灰锥托板上，再将托板固定在刚玉舟上，放置进湖南开元仪器公司生产的5E-AF3000智能灰熔融性测试仪中测定灰熔融温度[7]。测定的神东矿区部分煤的灰成分和灰熔点如表2所示。

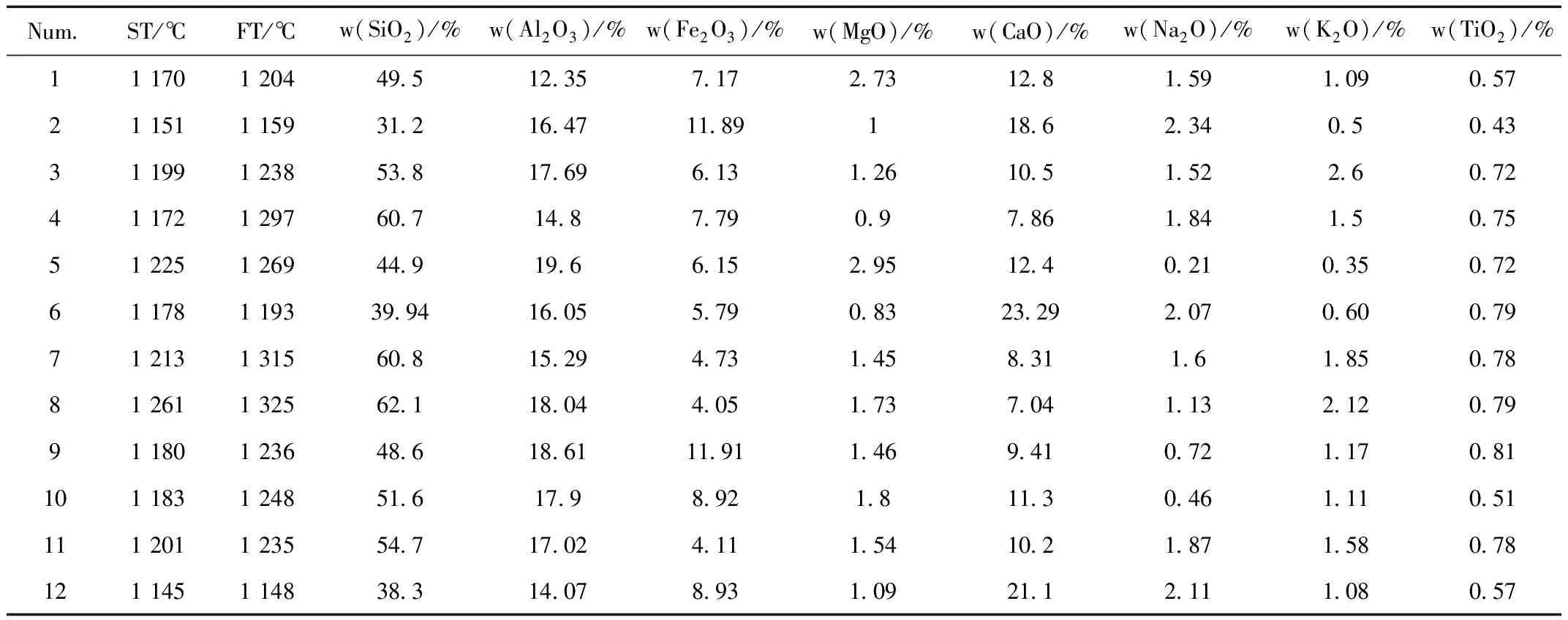
表2 神东矿区部分煤灰成分、ST和FTTable 2 Ash composition， ST and FT of partial coal at Shengdong mining area

神东矿区煤灰成分含量中铝含量比较低，这也导致了神东矿区的煤灰熔融温度偏低，酸碱比在0.17～1.10之间波动，通过酸碱比与煤灰熔融温度之间的关系来看，酸碱比小的煤灰熔融温度相对偏高。

2.2 数据预处理

本文采集了来自于神东矿区的100个煤灰灰成分数据，在训练集成CHAID决策树模型之前，对这100个煤灰灰成分数据进行数据相关性的分析，其实现方法为皮尔逊相关系数法，得到的煤灰灰成分与ST、FT的相关性见图2，图3所示。

图2 神东矿区煤灰成分与ST之间的相关性指数图Fig.2 Correlation index between coal ash composition and ST at Shendong mining area

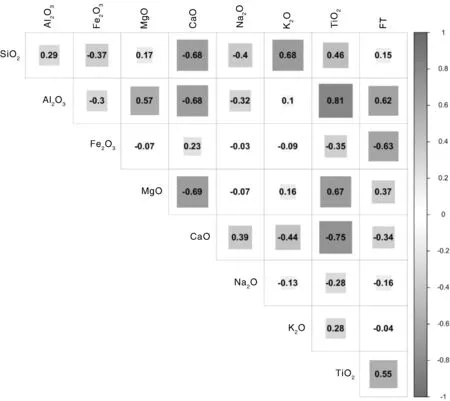
图3 神东矿区煤灰成分与FT之间的相关性指数图Fig.3 Correlation index between coal ash composition and FT at Shendong mining area

由图2，图3可知，神东矿区煤灰组分中Al2O3与ST和FT之间的相关性指数均为0.62，呈现强相关，TiO2与ST和FT之间的相关性指数分别为0.51和0.55，均呈现中等强度相关；而Fe2O3与FT之间的相关性指数达到-0.63，呈现强相关，Fe2O3与ST之间的相关性指数仅为-0.52，呈现中等强度相关[17]。

2.3 Bagging集成CHAID决策树的设计与训练

集成CHAID决策树模型输入量为神东矿区煤灰的8种成分，输出量为煤灰的2个特征温度，即煤灰的软化温度和流动温度。为了避免原始数据对模型训练精准度的干扰[18]，将100个神东矿区煤灰成分及特征温度数据随机划分为60%测试集和40%验证集，使用Bagging集成10棵CHAID决策树，每棵CHAID决策树的最大树深度设置为默认值5，模型收敛的最大迭代次数设为100次，目标中止规则使用百分比约束，当父分支中的最小记录数为2，子分支中的最小记录数为1时，模型停止训练。集成CHAID决策树模型的训练和检验通过SPSS分析软件实现。

3 模型评估方法

为评估Bagging集成CHAID决策树模型的可靠性和预测精度，利用训练好的模型对训练样本和检验样本的特征温度进行预测，并采用平均绝对误差(MAE)，标准差(SD)，线性相关系数R对模型的预测结果进行分析，分别定义如下：

(3)

(4)

4 结果与分析

4.1 CHAID决策树最大树深度对模型预测性能的影响

根据前面CHAID决策树最大树深度确定方法进行实验，考察CHAID决策树最大树深度对模型预测性能的影响。对不同最大树深度的模型均进行10次重复实验，实验目标误差设为0.0001，实验结果如图4所示。

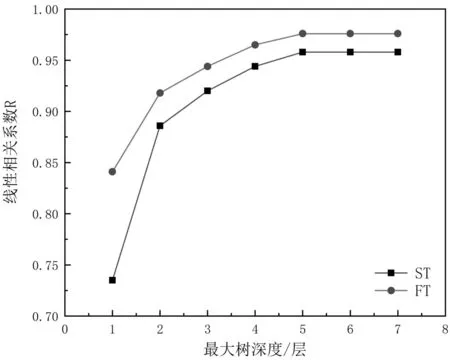
图4 不同最大树深度层数的模型对ST和FT的预测性能Fig.4 Performance of models with different maximum tree depth levels for ST and FT

从图4可知：随CHAID决策树最大树深度增加，模型预测结果的R值不断增大，并最终趋于定值，收敛速率逐渐变慢，当CHAID决策树最大树深度为5时，预测ST的R值达到最大值，为0.958，预测FT的R值同样达到最大值，为0.976，此时收敛速率最慢。这表明训练的时候生成的树层数越多，预测精度越高。但是达到一个临界值后可能会略有下降，这可能是因为过多的树深度会生成更多的树节点，导致分类的准确度下降的原因。因此，最大树深度的取值也不是越大越好[19]，综合模型预测精度和收敛速率，最佳的最大树深度为5。所以，集成CHAID决策树预测模型的最大树深度设置为5。

4.2 CHAID决策树个数对模型预测性能的影响

通过对CHAID决策树最大树深度对模型的影响分析后，进而考察CHAID决策树的个数对模型预测性能的影响，对不同决策树个数的模型进行10次重复实验，实验目标误差设为0.0001，实验结果如图5所示。

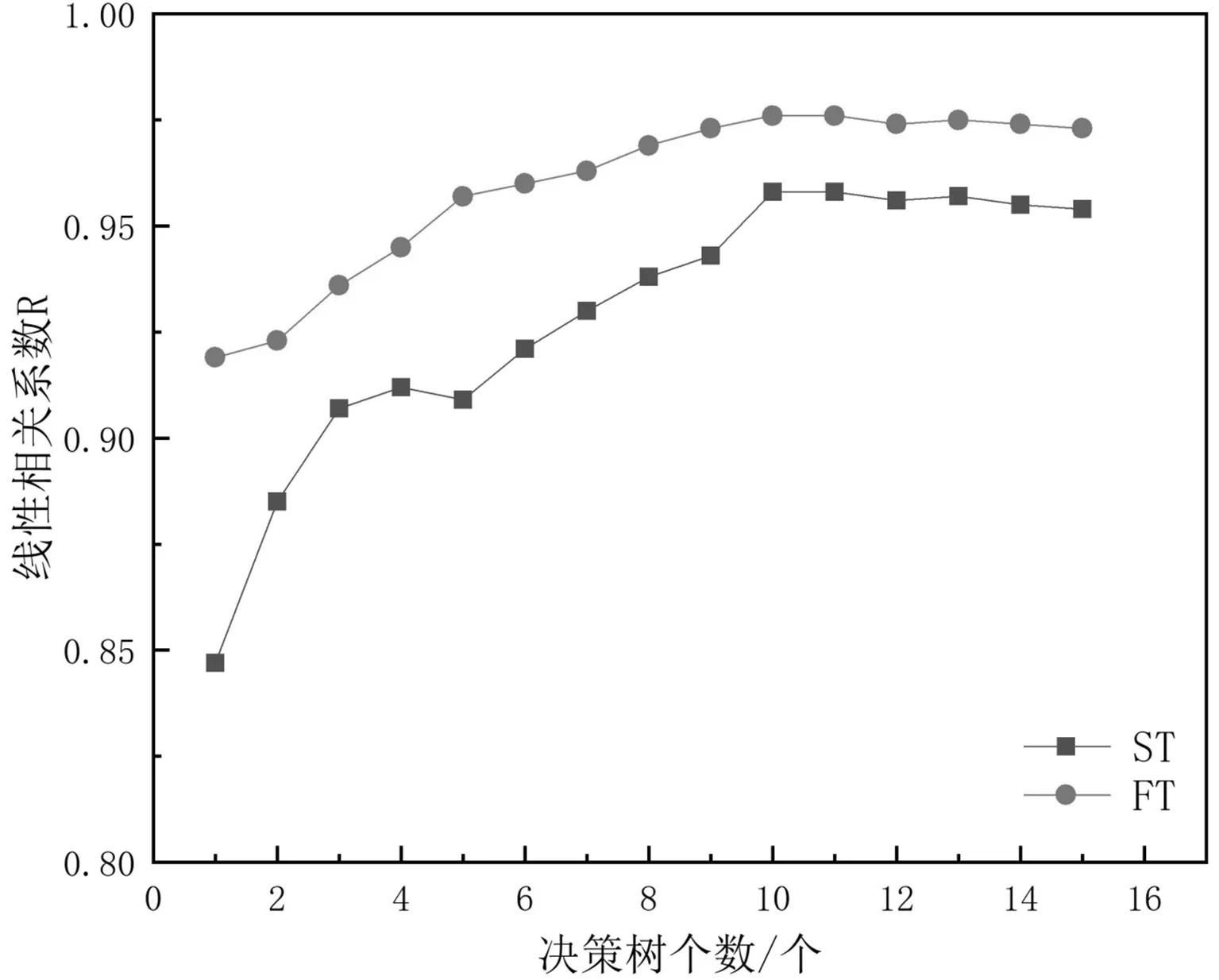
图5 不同决策树个数的模型对ST和FT的预测性能Fig.5 Performance of models with different numbers of decision trees for ST and FT

从图5可知：随CHAID决策树的个数增加，模型预测结果的R值不断增大，模型预测精度逐渐提高并最终趋于稳定，当CHAID决策树个数为10时，R达到了最大值，为0.976。这表明训练的时候生成的决策树个数越多，预测精度越高。但是因为数据集个数的限制，导致决策树的个数增加到一定量时，对预测精度的提升没有很大变化[20]。因此，对于CHAID决策树个数的取值也不是越大越好，综合模型预测精度和效果，对于本文的数据集来说，最佳的CHAID决策树个数为10。所以，使用Bagging集成10棵CHAID决策树进行模型的搭建。

4.3 模型检验结果与分析

为了验证集成CHAID决策树模型的预测性能，利用40个检验样本对其进行检验，效果如图6，图7所示。

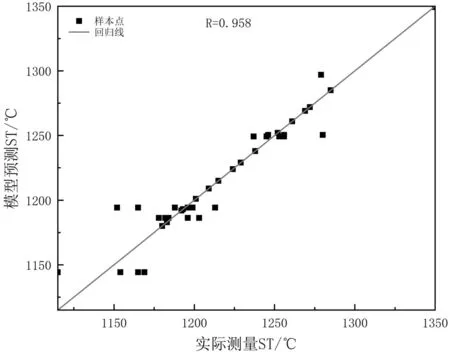
图6 ST预测线性回归分析结果Fig.6 Linear regression analysis results of ST prediction

图6和图7表示实际测量的ST和FT与模型预测ST和FT的相关程度，回归线为样本的实际测量温度，样本点为模型的预测温度，图6为模型预测ST的线性回归分析结果，线性回归相关系数为0.958，表明8个变量与ST有较好的线性相关性，图7为模型预测FT的线性回归分析结果，线性回归相关系数为0.976，表明8个变量与FT有极好的线性相关性，模型对FT的预测效果略好于对ST的预测。

图7 FT预测线性回归分析结果Fig.7 Linear regression analysis results of FT prediction

表3 模型对ST与FT预测结果的平均绝对误差与标准差的比较分析Table 3 Comparative analysis of mean absolute error and standard deviation of ST and FT prediction results by model

如上表所示，模型对于ST的预测误差范围在-43.879～63.867 ℃且对于FT的预测误差范围在-51.987～41.903 ℃，符合国家标准的-80～80 ℃的条件，说明本模型的预测效果较好，验证了其实用性能；模型对于预测ST的平均绝对误差为14.928，预测FT的平均绝对误差为12.238，说明预测结果与真实数据集的接近程度很小，模型的拟合效果较好；模型对于预测ST的标准差为19.406，预测FT的标准差为16.308，说明模型的误差波动较低，模型的稳定性较高，总体来看，模型对于FT的预测效果略好于预测ST。

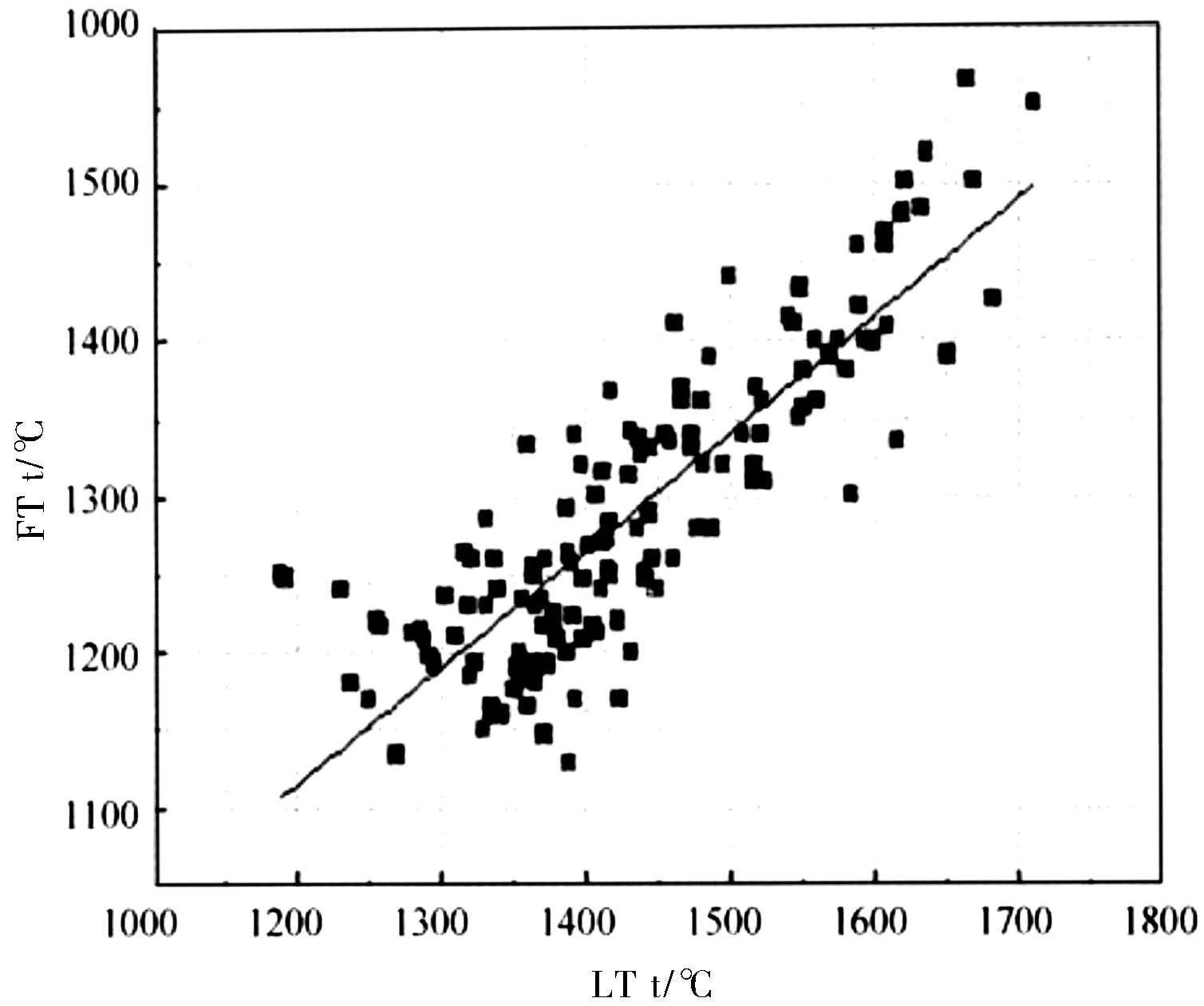
图8 灰流动温度与液相线温度之间的关系[21]Fig.8 Relationship of FT and LT

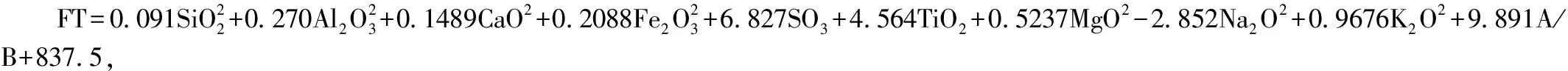
图8为FactSage软件建立的液相线温度与FT之间的相关性程度，从图8中回归线与样本点之间的离散程度与图7中的回归线与样本点之间的离散程度相比，Bagging集成CHAID决策树模型对于FT的预测效果更好，样本预测值更接近于实测值，预测精度高，泛化能力更强。

5 结 论

本研究以神东矿区煤灰成分中8种成分为自变量，ST和FT为因变量，建立了基于集成CHAID决策树算法的神东矿区煤灰熔融温度预测模型，很好的实现了灰熔融温度的预测，通过分析总结出以下结果：

(1)Bagging集成决策树的最大树深度以及决策树个数对模型的预测精度有较大影响，对本文数据集来说，集成CHAID决策树预测模型的最大树深度设置为5，且决策树个数设置为10时，对样本的预测效果最好。

(2)因本文模型训练样本数量为小样本，对于小样本数据集来说，Bagging集成CHAID决策树模型对ST与FT的预测精度都很高，对于ST的线性拟合的拟合度达到了0.958，对于FT的线性拟合的拟合度达到了0.976，说明模型对于FT的计算效率相比对于ST的计算效率更高，预测精度和泛化能力更强，适合对小样本FT预测。

(3)与多元线性拟合回归公式和FactSage软件建立公式相比，本文中的Bagging集成CHAID决策树模型对于ST与FT的预测相关性指数分别达到了0.958和0.976，比多元线性拟合回归公式的0.934和FactSage软件建立公式的0.924的相关性数值都要高，说明本文建立的模型预测精度要优于多元线性拟合回归公式和FactSage软件建立公式。

(4)利用Bagging集成决策树预测模型，可以为煤气化企业的气化炉运行等提供较精确的灰熔融温度预测，从而减轻并且抑制气化炉结渣，对气化炉的安全稳定运行提供重要指导。