数学实验：积累基本数学经验的有效载体——以“直线的倾斜角与斜率”教学设计为例

徐长俊

一、引言

当前的中职数学教学缺少让学生形成基本数学经验的环节，导致学生难以理解有些抽象的数学概念或者结论，抽象性是中职学生学习数学过程中的最大障碍。“基本数学经验”是指在数学目标的指引下，通过对具体事物进行实际操作、考察和思考，从感性向理性飞跃时所形成的认识。中职数学教师基本都是由普通高中考入大学的，受普通高中的传统教学方法耳濡目染，自然也成为自己的教学习惯，但是对中职学生用演绎和推理的方法讲解抽象的数学知识，显然是行不通的。

学生的基本数学经验要从数学活动中获得，数学实验恰好提供了一个很好的数学活动的形式。数学家波利亚曾说：“数学既是一门系统性的演绎科学又是一种实验性的归纳科学。”因此,有必要将数学实验融入数学课堂教学设计中。数学实验可以分成传统数学实验和现代数学实验。传统数学实验是指利用实物模型或数学教具进行实验，现代数学实验是指以计算机数学软件的应用为平台进行的实验。数学中需要“动态”呈现的“图形与几何”等问题利用传统实验手段难以实现。相比较而言，以计算机软件为平台的现代数学实验在这方面具有极大的优势。

对于学习数学普遍没有积极性，数学思维能力又不足的中职学生，数学实验能够让其在动手操作的过程中归纳数学知识，从晦涩难懂的演绎推理中解放出来，从数学学习的“旁观者”变成“发现者”，帮助学生在积累数学活动经验的同时经历数学知识的发生和发展过程，让数学知识的学习不再枯燥无味。数学实验可以有力促进中职学生数学思维品质和关键能力的提高。

本文以“直线的倾斜角与斜率”的教学设计为例，谈一谈笔者在中职数学教学中引入数学实验的一些尝试。

二、教学过程

（一）创设时代情境，导入新知

让学生观看苏通大桥短视频（如图1）。

图1

（教师旁白）苏通大桥位于南通和苏州之间，跨径为1088 米，是当今世界跨径最大、基础最深、桥塔最高、拉索最长斜拉桥。

师：看完这段视频，我们的感受是……

生：宏伟、国家的强大……

师：从苏通大桥的斜拉索我们能抽象出什么几何图形？

生：直线。

（二）设计探究实验，感知新知

以下实验都是在GeoGebra 软件中进行。

实验1：指导学生完成斜拉桥的绘图（如图 2）。

图2

实验目的：通过画斜拉桥，实际体会确定一条直线的条件，同时感知实际生活中的数学美。

师：图2 中斜拉索所在直线相对于桥边线的倾斜程度是否相同？

生：有些相同，有些不同。

师：我们用什么量刻画斜拉索的倾斜程度？

生思考……

师：用斜拉索所在直线与桥边线的夹角刻画斜拉索的倾斜程度，像这样的角称为倾斜角。

实验2：指导学生在GeoGebra 软件中转动如图3 的直线。

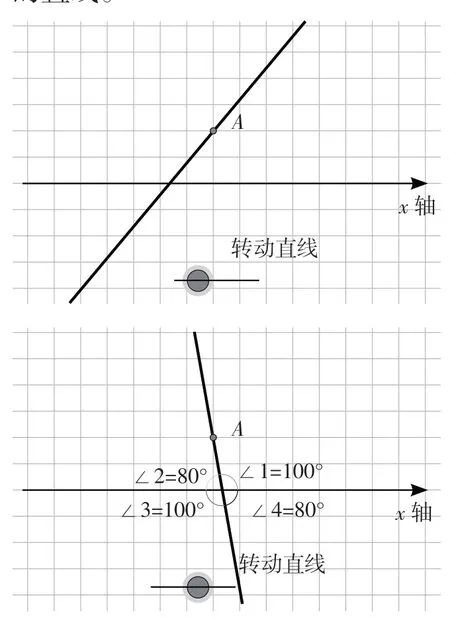
图3

实验目的：让学生在实验过程中感知倾斜角定义的过程。

师：两直线相交构成四个角，你们选择哪一个角刻画直线的倾斜程度比较合适。

生：角1。

师：如何描述这个角？

生思考……

师：倾斜角的定义。

倾斜角：直线与x 轴相交时，直线向上的方向与x 轴所夹最小正角。

师：我们知道已知两点可以确定一条直线，如果直线过点A、B，倾斜角为，那么这两个点的坐标与倾斜角是不是存在某种关系？

生思考……

实验3：指导学生在GeoGebra 软件中（如图4 和图5）作出经过两点直线的倾斜角。

图4

图5

实验目的：引导学生在实验过程中体会并归纳倾斜角与两点的坐标变化之间的关系。

师：观察图4 和图5，归纳倾斜角和两点的坐标有什么关系？

师：这个比值和坡度的定义很类似，我们定义为斜率，斜率和倾斜角的关系很显然就是k=tanα。

（三）设计尝试实验，理解新知

实验4：指导学生（如图6）在GeoGebra 软件中移动点的位置，使得直线的斜率等于所给的值。

图6

实验目的：软件可以不断地随机提出类似问题，学生用不同的方法反复尝试和检验，过程中有可能会反复出现失败。学生在对照公式的不断试错中，逐渐理解已知两点坐标求直线斜率的公式的几何意义。

（四）设计类比实验，应用新知

实验5：小明早晨去爬山，如图7，请问他爬哪段山坡会比较吃力？

图7

设计目的：判断哪段山坡比较吃力当然不能完全靠感觉。此实验引导学生将直线的斜率定义和初中已经接触过的“坡度”概念进行类比，学会用数据“说话”，解决生活中的一些实际问题。

三、几点思考

（一）基于数学实验的中职数学教学设计的必要性

某些抽象的数学知识与生产和生活中的实际问题存在紧密联系。学生在脱离实际问题的教学活动中难以获得这些数学知识的深刻理解，也难以牢固记忆相关的概念和公式。教师可以利用数学实验将抽象直观化、可视化，可以引导学生亲身经历一个概念形成过程，引导学生感悟知识发生过程、理解知识结果。

数学学科核心素养的生成是数学知识、问题解决、数学思维联结融合的结果。数学知识是数学学科核心素养形成的关键载体, 学生在解决问题中才能真正认识数学知识，生成数学思维能力。有很多数学知识是动态的，或者是比较抽象的，缺乏基本数学经验的中职学生在理解教师用系统演绎的方法讲解数学知识的过程中障碍很大。

（二）基于数学实验的中职数学教学设计的可行性

数学实验是在教师引导下，学生在动手动脑中完成的数学活动，数学实验是能充分展示探究过程的教与学的活动。数学实验要能给学生提供一个动手解决数学问题的平台，在情境导入环节，在知识和概念的引入环节，在知识巩固环节都可以设计适当的数学实验，让学生从具象中归纳出抽象的数学知识。数学实验是要能让学生在解决一个个问题过程中经历不断的尝试、观察和归纳的数学活动，积累丰富的数学活动经验。

但是，一方面，学生要完成传统的数学实验有时需要花大量时间，效率低，中职学生学习数学的时间是非常少的，同时实验过程和结果也难以掌控。另一方面，传统的数学实验需要教师准备大量的材料，消费巨大，难以承受。数学实验在引入中职数学课堂教学中困难重重，而基于计算机技术的现代数学实验能很好解决上述问题。计算机软件能简化和模拟实际问题，易于学生对实验进行反复操作、观察和归纳数学活动，大大提高了教学效率。实验也不需要准备一大堆材料，便于教师在以后的教学活动中反复使用和改进。

（三）基于数学实验的中职数学教学设计的注意点

1.教师是数学实验的设计者。要将数学实验引入中职数学课堂，作为数学教师不能将别人设计好的数学实验拿来就用，教师自己必须有设计数学实验的能力。这些能力包括：（1）熟练掌握至少一个数学软件，如GeoGebra、几何画板、Maple 等；（2）大量阅读数学实验设计的案例，模仿案例设计自己需要的数学实验；（3）熟知中职学生的认知能力和特点，这样才能站在学生角度设计出学生能够完成的数学实验，才能引导学生在数学实验中发现和探索。

2.实验要用适当问题驱动。数学实验必须要有目的，学生操作数学实验要解决一个具体的问题。教师设计的数学实验要能让学生在做实验的过程中自主观察、思考并且归纳结论，继而回答教师提出的一个个问题。当然，这个问题不能过于简单，必须是学生直接思考难以回答的问题，这样我们的实验才有意义，才能真正让学生在实验过程中有所收获。问题也不能过于复杂，否则设计的数学实验也必然复杂，可以将复杂的问题分解成几个连贯的适当的问题，相应设计几个简单数学实验。

3.实验要易于学生操作和观察。教师设计的数学实验的操作不能复杂。除了实验必须有明确的目的之外，利用计算机软件设计的虚拟实验还要简单明了，易于学生操作。过于复杂的实验，学生会不知道如何下手。教师设计实验时可以适当加一些文字引导或者说明，一步步引导学生操作、观察和归纳，教师在学生做实验时也要适时加以指导。

4.实验的设计要以学生为主体。数学实验的主体是学生，必须要由学生完成实验的所有过程，绝对不能是教师做实验展示给学生看。数学实验的目的就是要让学生在“做中思”，在“做中学”，让学生成为知识发现的亲历者。教师不能因为图省时间、赶进度而剥夺学生参与数学活动的机会。只有充分尊重学生主体地位的数学实验，才能让学生真正获得基本数学经验，也才能培养学生的数学素养，促进学生综合素养的提升。