基于共轭梯度的MARG传感器姿态解算方法

戚文昊， 刘 宁， 苏 中， 乔利康， 王靖骁

(1.北京信息科技大学高动态导航技术北京市重点实验室，北京 100000；2.现代测控技术教育部重点实验室，北京 100000)

0 引言

飞行器姿态解算对飞行器的导航与控制具有重要意义，基于IMU的姿态解算方法精度低、噪声大，且无法准确测量飞行器在偏航方向上的姿态变化，而采用多传感器数据融合的方法能有效提高飞行器姿态解算精度[1]。目前，由陀螺仪、加速度计和磁强计组成的MARG传感器系统受到广泛关注，对MARG传感器数据进行互补融合，实现飞行器姿态参数的最佳估计，是当前姿态解算的重要研究内容[2]。

目前，飞行器姿态解算的数据融合方法主要有互补滤波算法、扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)和容积卡尔曼滤波等[3]。其中，典型的互补滤波算法简单可靠，对传感模块的精度要求较低，可以综合多传感器各自频率响应优势，以减小姿态测量和估计的偏差，但无法确定高通与低通滤波器截止频率，因此精度不高[4]；EKF是应用最为广泛的一种非线性滤波方法，但存在线性化误差、截断误差以及容易发散等问题[5-6]；在文献[7-9]中，将UKF应用于姿态解算，在收敛速度和估计精度中要高于EKF，但其计算量要比EKF大，并且它们的系统噪声和观测噪声不易确定，解算的姿态角容易受到噪声干扰；文献[10]中提到的容积卡尔曼滤波虽然精度高于EKF，但对计算能力提出了更高的要求。

本文提出一种基于共轭梯度算法的MARG传感器姿态解算方法，能够在梯度下降算法的基础上提高收敛速度，又可以避免卡尔曼滤波算法计算量大的缺点。利用加速度计和磁强计建立飞行器姿态误差函数，采用共轭梯度方法求解误差函数最小值，对飞行器姿态四元数进行最优估计，修正更新陀螺仪测量的飞行器姿态，最终将陀螺仪测量的飞行器姿态四元数和共轭梯度算法求解的姿态四元数进行加权融合，解算出姿态角。

1 四元数姿态表示

1.1 坐标系建立

上述方法在姿态解算中存在奇异性问题，本文采用四元数姿态表达式。在四元数姿态表达式中，一个坐标系到另一个坐标系的变换可以通过绕一个定义在参考坐标系中的方向矢量r进行单次转动角度α来实现。坐标系转换示意图见图1。

图1 坐标系转换示意图Fig.1 Diagram of coordinate system conversion

1.2 四元数姿态更新

陀螺仪在载体坐标系下三轴的角速率输出分别为ωx，ωy和ωz，转换为四元数形式可以表示为bω=[0ωxωyωz]。

(1)

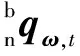
(2)

式中，Δt为采样周期。

2 姿态解算方法

2.1 传感器模型

(3)

(4)

(5)

2.2 共轭梯度算法

根据传感器模型得到加速度计和磁强计各自的误差函数，在共轭梯度算法中，为了寻找目标误差函数的极值，需要计算误差函数fg,▽对应的雅可比矩阵Jg,▽

(6)

最终可以采用共轭梯度法进行姿态四元数更新，即

(7)

式中：λt-1为姿态更新的最优步长；dt-1为姿态更新的搜索方向，算式如下[14]

(8)

式中,gt为目标函数在t时刻的迭代梯度。为了使共轭梯度方法计算得到的姿态四元数接下来可以与陀螺仪估计的姿态四元数进行加权融合，通过共轭梯度方法更新姿态四元数时每次采样只迭代一次。

2.3 数据融合

(9)

式中，γt为融合加权系数。为了使共轭梯度算法的收敛速度与陀螺仪解算姿态的发散速度相同，即(1-γt)β=γtλt/Δt，则应使姿态更新的步长λt尽可能大，γt可化简为

(10)

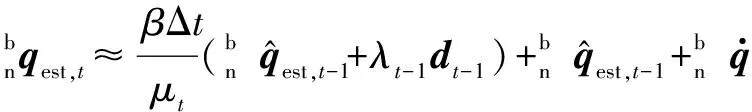
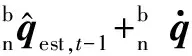
(11)

图2 共轭梯度算法流程图Fig.2 Flow chart of conjugate gradient method

3 仿真试验与结果分析

为了验证所提姿态测量方法的有效性和准确性，设计一种包含加速度计、陀螺仪、磁强计的MARG传感器系统的测量装置。测量装置和试验环境如图3所示。

图3 测量装置和试验环境Fig.3 Measuring device and test environment

3.1 静态试验

将测量装置静止放置于隔振台上，静止采集数据45 min，采用不同方法对测量装置姿态角进行解算，计算并比较不同算法在静止状态下的姿态角偏移误差。不同算法的姿态解算结果如图4所示；计算并汇总静态试验下两种方法的误差如表1所示。

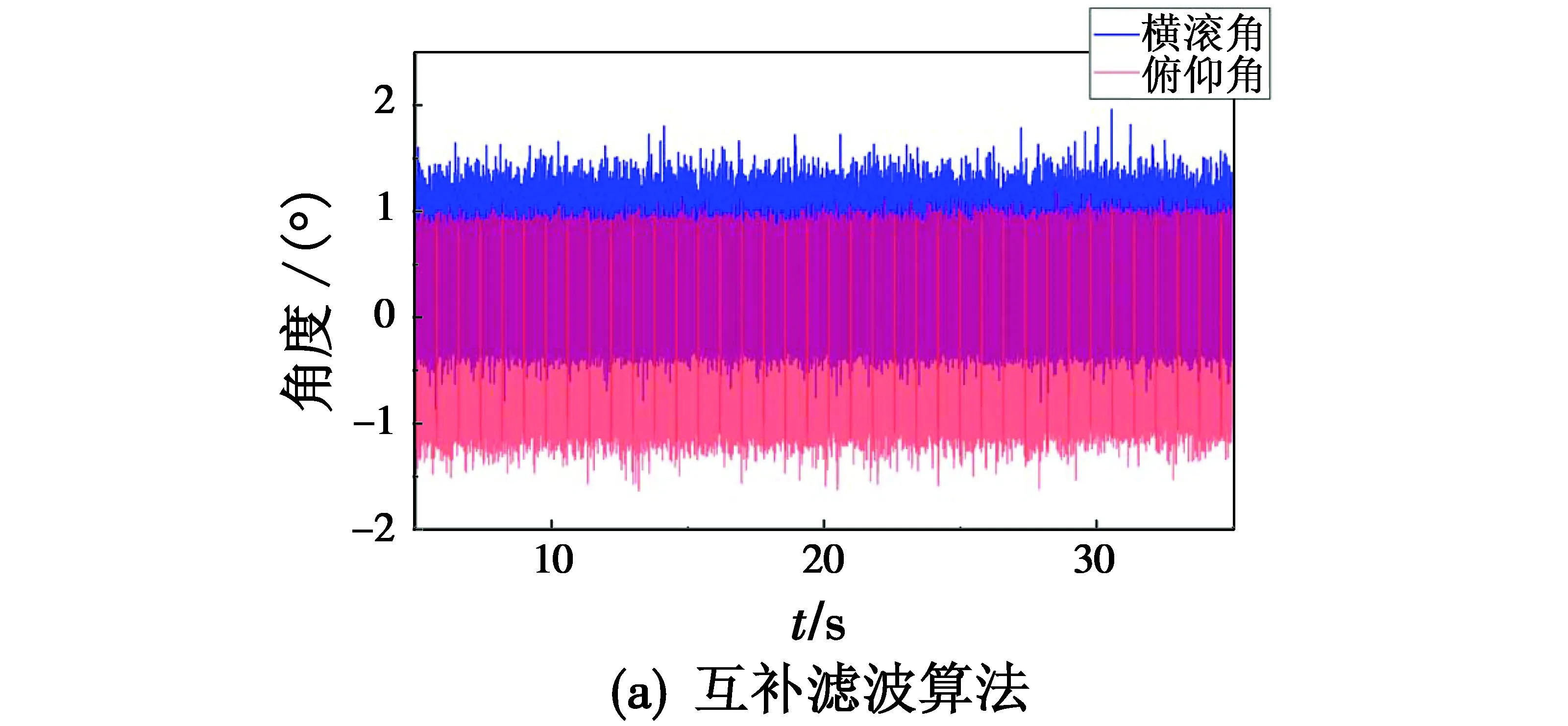
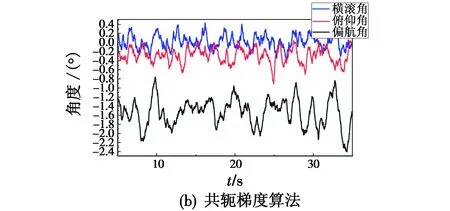
图4 不同算法的姿态解算结果

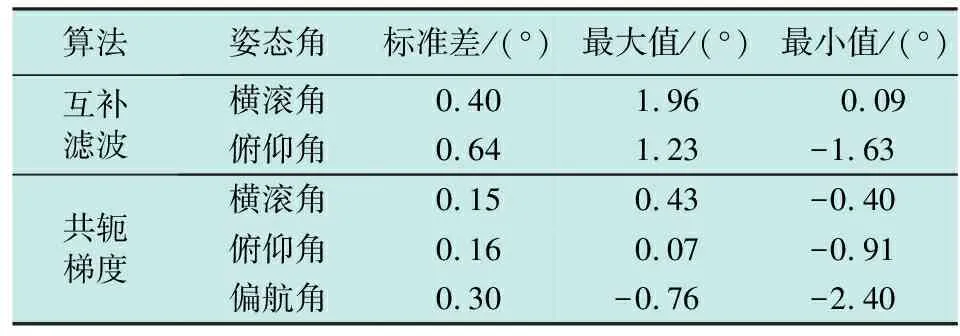
表1 静态试验姿态解算误差

由该组静态试验对比可以得到，静态时共轭梯度算法的波动范围和标准差均小于传统互补滤波算法，说明共轭梯度算法相比传统姿态解算方法具有更强的稳定性。

3.2 动态试验

将测量装置固连于三轴转台中心，控制三轴转台围绕测量装置的x，y，z轴依次转动至-80°，80°位置，重复两次。分别采用共轭梯度法、互补滤波法、扩展卡尔曼滤波(EKF)以及角速率积分方法对测试数据进行姿态解算，姿态解算结果如图5所示。为了便于区分，不同算法在纵向进行了适当偏移。

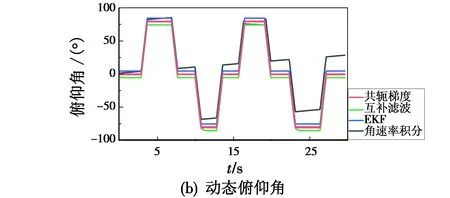
图5 姿态解算结果

分别计算不同算法解算姿态角与真实值之间的误差，得到横滚角、俯仰角和偏航角的误差对比，如图6所示。

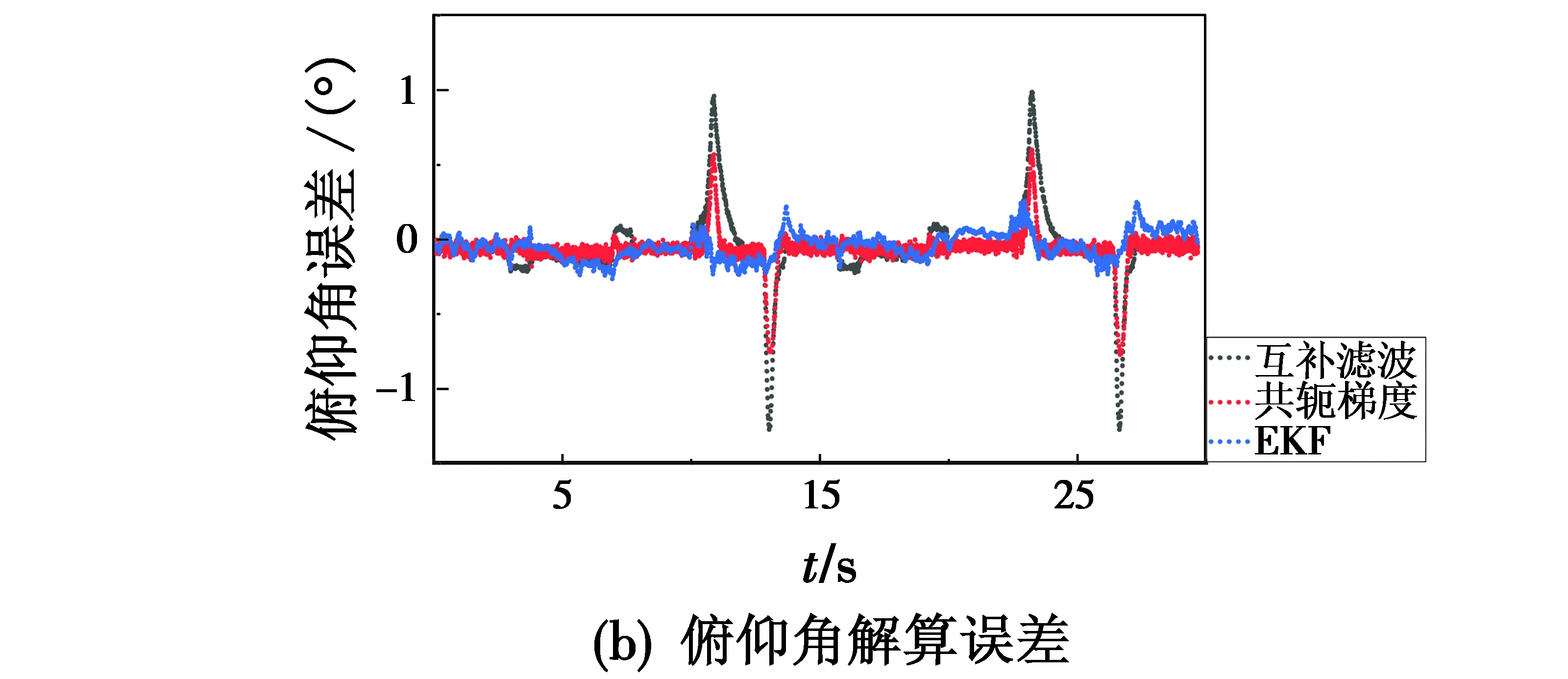
图6 姿态解算误差

由图6可以得到，本文提出的共轭梯度算法可以有效抑制陀螺仪输出姿态的发散问题，相比于互补滤波算法，具有更好的动态性能，收敛速度更快，解算精度与EKF相差不大，但能够有效降低系统运算压力。最后，计算并汇总3种算法的均方根误差(RMSE)，如表2所示。

表2 动态试验姿态解算RMSE

4 结论

本文提出了一种共轭梯度算法，用于解算MARG传感器系统的姿态，利用加速度计和磁强计构建误差函数，对姿态四元数进行补偿和修正，并对多传感器数据进行加权融合，以提高姿态解算精度。试验结果表明，相较于以IMU为基础的姿态解算方法，本文提出的算法在静态时具有良好的抑制噪声和抑制漂移的能力，在动态环境下具有更好的性能及更高的解算精度。