随队支援干扰下编队协同攻击航路规划
2022-08-11袁万勇
刘 琨, 袁万勇, 张 洁
(中国飞行试验研究院,西安 710000)
0 引言
编队协同航路规划是保障作战编队有效协同的关键技术[1]。国内外学者针对协同航路规划中的航路可飞性、障碍规避、冲突规避等方面进行大量研究[2-7],但是考虑编队内作战单元的任务属性协同航路规划的研究相对较少。空中编队执行对地攻击时,随队电子支援干扰将为编队突防力量提供掩护支持,同时对编队作战单元时/空协同自主规划能力提出需求。
本文首先对随队支援干扰编队协同攻击航路的协同约束条件进行分析建模,其次以攻击时序为基础设计了多机航路综合评价函数,最后设计了一种动态协同导引因子以解决编队协同攻击的航路规划问题。
1 随队支援编队协同航路规划问题
1.1 编队航行约束条件
作战想定:空中攻击编队由1架执行支援(即软杀伤)的干扰机(1号战机)与2架实施硬摧毁的攻击机(2号和3号战机)组成,编队执行任务场景如图1所示。
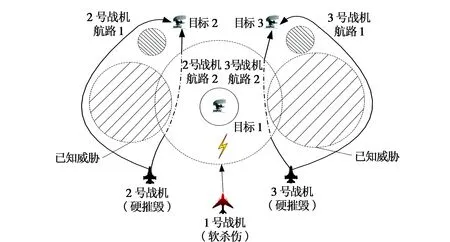
图1 编队协同攻击航路规划Fig.1 Formation coordinated attack route planning
假设编队内战机集合F={Fi,i=1,2,…,M},攻击目标集合T={Tj,j=1,2,…,K},威胁范围集合M={Mk,k=1,2,…,Nm},任务起始点集合S={Si,i=1,2,…,M},速度范围为[vmin,vmax]。
编队航行约束主要分为编队空间协同约束与时间协同约束两方面[8-9]。下面将分别针对这两方面约束进行讨论。
1) 空间协同约束。
空中编队执行任务过程中,任意时刻各战机间必须保证安全距离以防止与友机相撞。设第i架战机与第i*架战机在t时刻的位置分别为Pi(t)与Pi*(t),空中安全距离为ds,即任意时刻2架战机的欧氏距离大于等于ds,即
‖Pi(t)-Pi*(t)‖≥dsi,i*=1,2,…,M,i≠i*。
(1)
2) 时间协同约束。
时间协同约束需满足以下条件:① 随队支援飞机攻击目标的时刻要早于被掩护战机的攻击时刻;② 随队支援飞机攻击目标j的时刻要早于被掩护战机飞入目标j威胁区域。
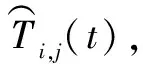
(2)
设战机m飞入目标j威胁区域的时刻为Mm,j(t),则约束表示为
(3)
1.2 单机航路规划评价函数
单机航路规划的指标主要包括能耗代价与威胁代价两类指标。对单机航路综合代价进行适当简化并表示为

(4)
式中:L为路径长度;Cr(s)为航路s点处的雷达威胁代价;Cm(s)为航路s点处的地空导弹威胁代价;Cg(s)为航路s点处的高炮威胁代价。系数δr,δm,δg分别为各代价的权重且满足
δ=δr+δm+δg=1。
(5)
1.3 编队协同航路规划评价函数
航路筛选通过协同航路评价函数选择出满足约束的最优编队航行轨迹。假设战机Fi,i=1,2,…,M的单机航路代价为Ci,i=1,2,…,M,编队协同航路代价记为C∑,其函数表示为
C∑=f(C1,C2,…,CM)。
(6)
为简化编队协同航路评价模型,引入航迹协同系数λ来衡量编队协同攻击航路集对时间约束的满足程度,其表达式为
(7)
式中,λi为战机Fi规划航路Li的航路协同系数。协同系数的设计准则如下:执行随队干扰飞机不进行惩罚,仅在执行硬摧毁攻击的战机航路不满足任务时序约束要求时,将通过协同系数对其航路评价值进行惩罚。
执行硬摧毁战机Fi的航路Lm的协同系数为
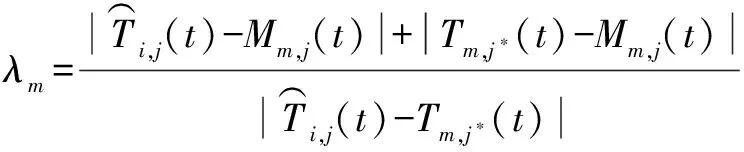
(8)
编队协同攻击航路规划的优化目标量化为多机协同航路综合评价指标最小化,其表达式为
(9)
1.4 战场威胁环境建模
假设作战区域内共有Np部对空警戒雷达、Nq处防空导弹阵地、Ns处高炮阵地,则分解为直线航路段后单机综合航路代价模型为
(10)
(11)
式中:C(Li,i+1)为战机经过航路段Li,i+1所受威胁程度的大小;Cr,p(Li,i+1)为第p部雷达对战机Li,i+1航路段的威胁代价;Cm,q(Li,i+1)为第q处防空导弹阵地对战机Li,i+1航路段的威胁代价;Cg,s(Li,i+1)为第s处高炮阵地对战机Li,i+1航路段的威胁代价。
航路段Li,i+1威胁代价可以近似表示为5个航路节点到威胁源的威胁代价之和。航路段Li,i+1的威胁代价算式为
C(Li,i+1)=(C(di,k1)+C(di,k2)+C(di,k3)+
C(di,k4)+C(di,k5))/5。
(12)
1) 雷达威胁模型。
航路规划问题中,通常将雷达对战机的发现概率表示为雷达对战机航路的威胁代价[10]。规划区域内第p部雷达对战机航路段Li,i+1的威胁代价表示为
(13)
式中:dR表示战机规划航路段Li,i+1与雷达p的距离;dRmax,dRmin分别为雷达最大探测距离与雷达高危探测范围;δφ为动态RCS计算模型,其表达式为
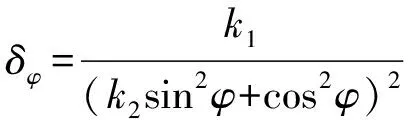
(14)
式中:参数k1=0.01,k2=0.1;φ为进入角。当雷达p遭受干扰攻击时,其丧失对目标的探测能力,故将战机Li,i+1航路段威胁代价变为
Cr,p(Li,i+1)=0 ∀dR。
(15)
2) 导弹威胁模型。
防空导弹对航路威胁代价主要体现为对战机的杀伤概率。第q处防空导弹阵地对战机航路段Li,i+1威胁代价表示为
(16)
γv=1+(vmax-vi)·(vmax-vmin)-1
(17)
式中:dM表示战机规划航路段Li,i+1与第q处防空导弹阵地的距离;dMmax,dMmin分别为防空导弹的最大攻击距离与不可逃逸攻击距离;γv为威胁值随战机速度vi增加而衰减的系数。
3) 高炮威胁模型。
在一定的初速度下,火炮射击包线即为高炮的杀伤区域,第s处高炮阵地对战机航路段Li,i+1的威胁代价表示为
(18)
式中,dG表示战机规划航路段Li,i+1与第s处高炮阵地的距离;dGmax,dGmin分别表示高炮的最大射程与封锁空域范围。
2 基于协同引导因子多蚁群求解编队航路
2.1 基于异质信息多子群协同进化机制
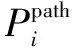
(19)
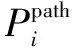
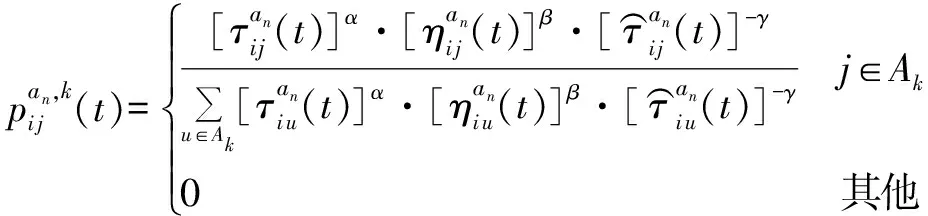
(20)
式中:γ为相异种群信息素互斥系数;Ak为蚂蚁k由当前位置可移动至下一航路点的集合。
2.2 动态目标引导因子设计
标准蚁群算法中,状态转移概率主要由信息素和启发因子决定。为提高算法搜索效率,避免盲目搜索造成的时间损耗,文献[11-12]提出目标导引因子,引导蚁群向目标航路点进化,其表达式为
(21)
式中,(xi,yi),(xtarget,ytarget)分别表示航路点i与目标点的位置坐标。式(20)变为

(22)
式中,χ为目标导引因子的决策系数。目标导引因子的引入可以在一定程度上增强蚂蚁个体搜索的目的性,提高算法搜索效率。
执行硬摧毁任务的战机若将目标引导点直接设置为待攻击目标会存在穿越威胁区域情况,影响算法搜索有效率。针对该问题,提出动态虚拟目标引导因子。虚拟初始点位置如图2所示,根据载机飞行速度逐步移动至待打击目标点。

图2 动态虚拟目标导引位置点Fig.2 Dynamic virtual target guidance position point
设2号战机进入目标雷达1的探测边缘位置与虚拟导引点的距离为DAS,战机平均飞行速度为Va,虚拟导引点与最终目标导引点间直线距离为DST,虚拟目标导引点移动速度为Vs。
设虚拟导引点(xs,ys)的移动增量分别为Δxs,Δys,则
(23)
式中,ta表示战机2在雷达1探测范围内的飞行时间,当战机2飞入其探测范围内,ta开始计时,虚拟目标导引点位置开始移动,直至目标雷达2。其表达式为
(24)
以上详细介绍了协同导引因子的设计,编队协同攻击航路规划求解过程如图3所示。
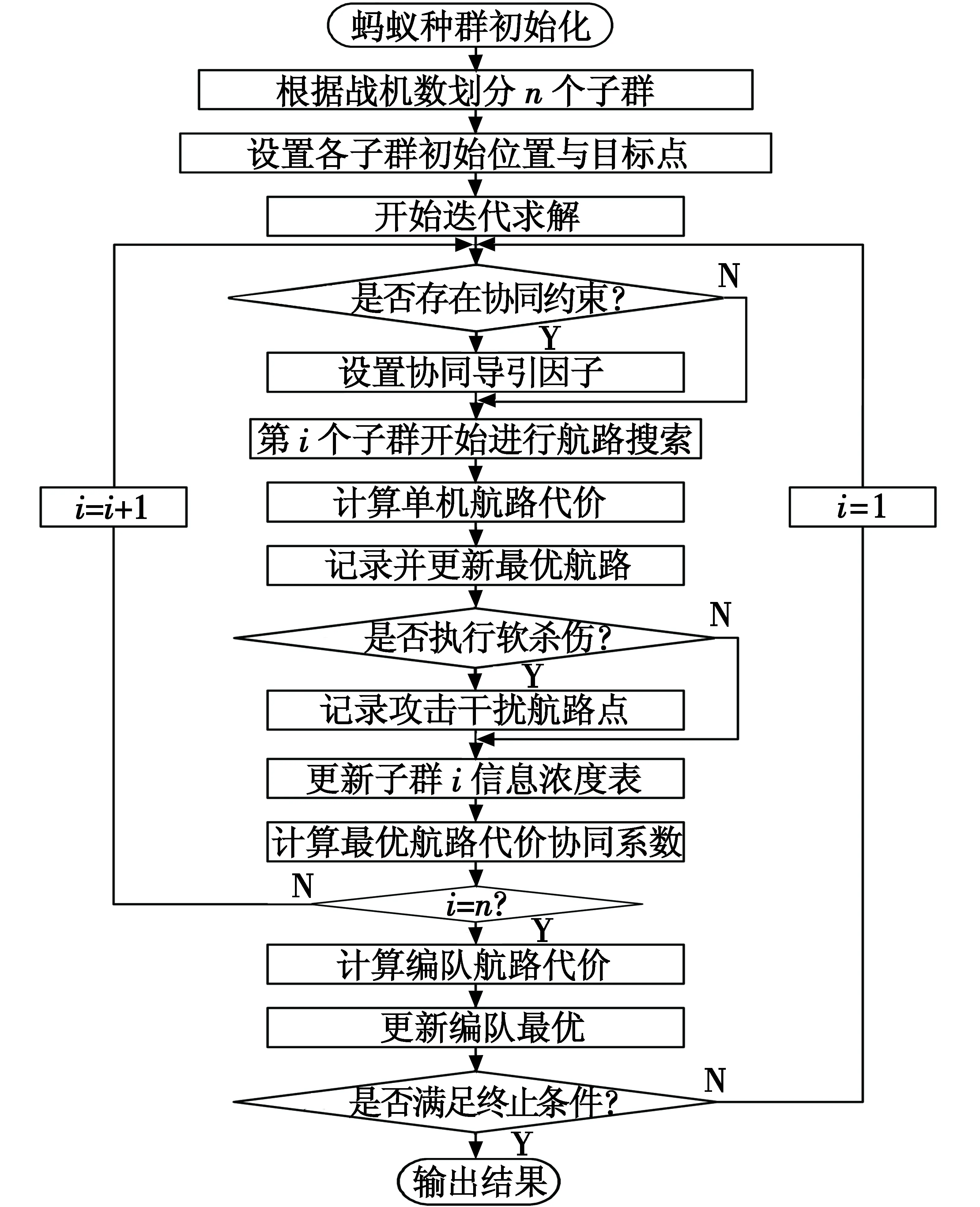
图3 协同攻击航路规划求解过程Fig.3 Coordinated attack route planning process
3 仿真实验与分析
仿真软件为Matlab R2010a。采用200 km×200 km二维地图,X轴方向网格划分步长Nx=1,Y轴方向网格规划步长Ny=1。规划空间中威胁源信息见表1。

表1 算例1威胁源信息
编队与目标位置信息见表2。
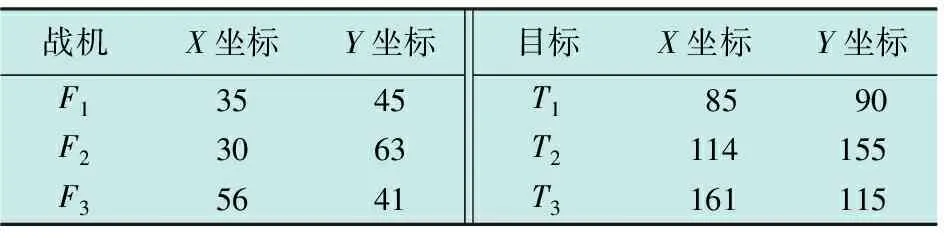
表2 算例1编队与目标位置信息
设置蚂蚁种群中蚂蚁总数为30,将整个种群均分为3个种群。假设编队内3架战机飞行速度均为Va=400 m/s。信息素调节决策系数α=1,启发因子决策系数β=0.25,目标引导因子决策系数χ=8,互斥因子决策系数γ=0.3;信息增强系数Q=6,信息素挥发系数ρ=0.65;航路段各威胁源权重设置为:δr=0.4,δm=0.4,δg=0.2。迭代次数设置为300,分别利用本文提出的改进蚁群算法与标准蚁群算法进行航路求解,编队最优航迹对比见图4。


图4 最优航迹对比分析图
图4中,2种算法为3架战机规划的航路均满足空间协同约束,即航迹不发生交叉。通过对比观察,本文提出的改进蚁群算法求解的航路更为平滑,战机综合航路代价较小。
通过种群最优值对比曲线分析可知,本文所提改进蚁群算法的收敛速度在迭代20次内较标准蚁群算法更快,在迭代50次内可快速收敛逼近最优解。改进蚁群算法初始解算种群最优值较标准蚁群算法提高70%以上,求解最优解准确性与有效性较标准蚁群算法也有较大提升。
编队协同攻击时,将连续对敌方阵地实施突击,故本文增加解算难度验证算法针对连续任务航路的规划能力。战场环境设置见表3~5。
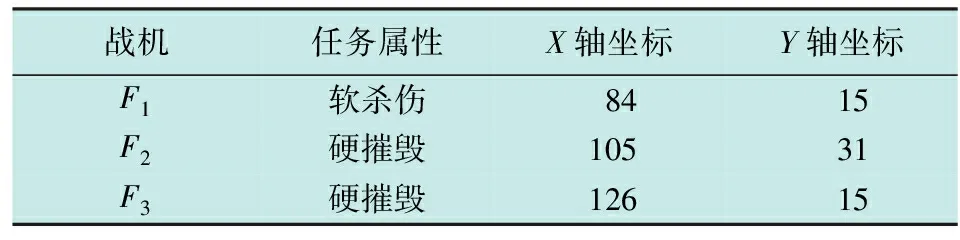
表3 算例2战机初始位置及任务属性
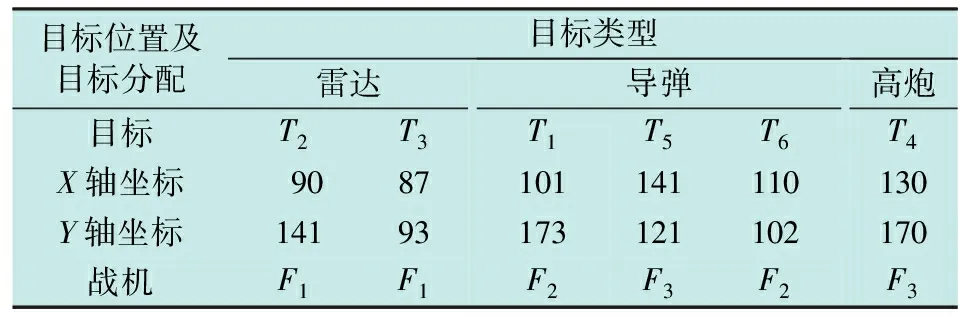
表4 算例2目标位置及目标分配
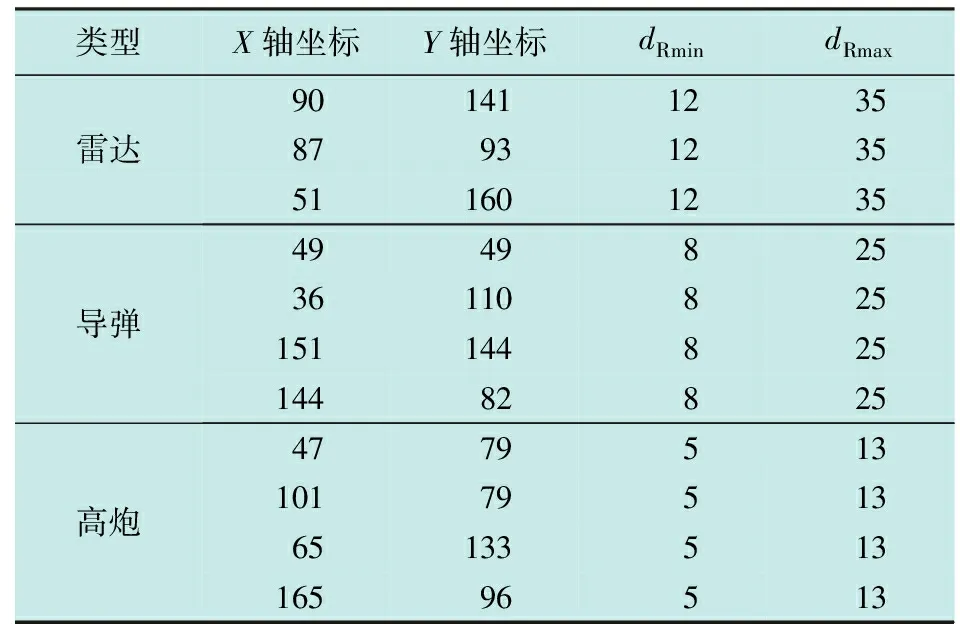
表5 算例2威胁源信息
图5所示为第一阶段编队飞行航路。
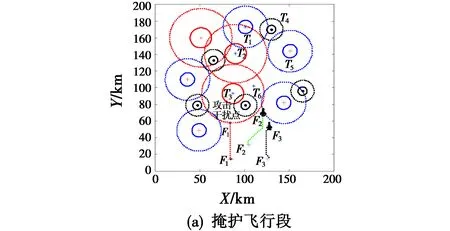
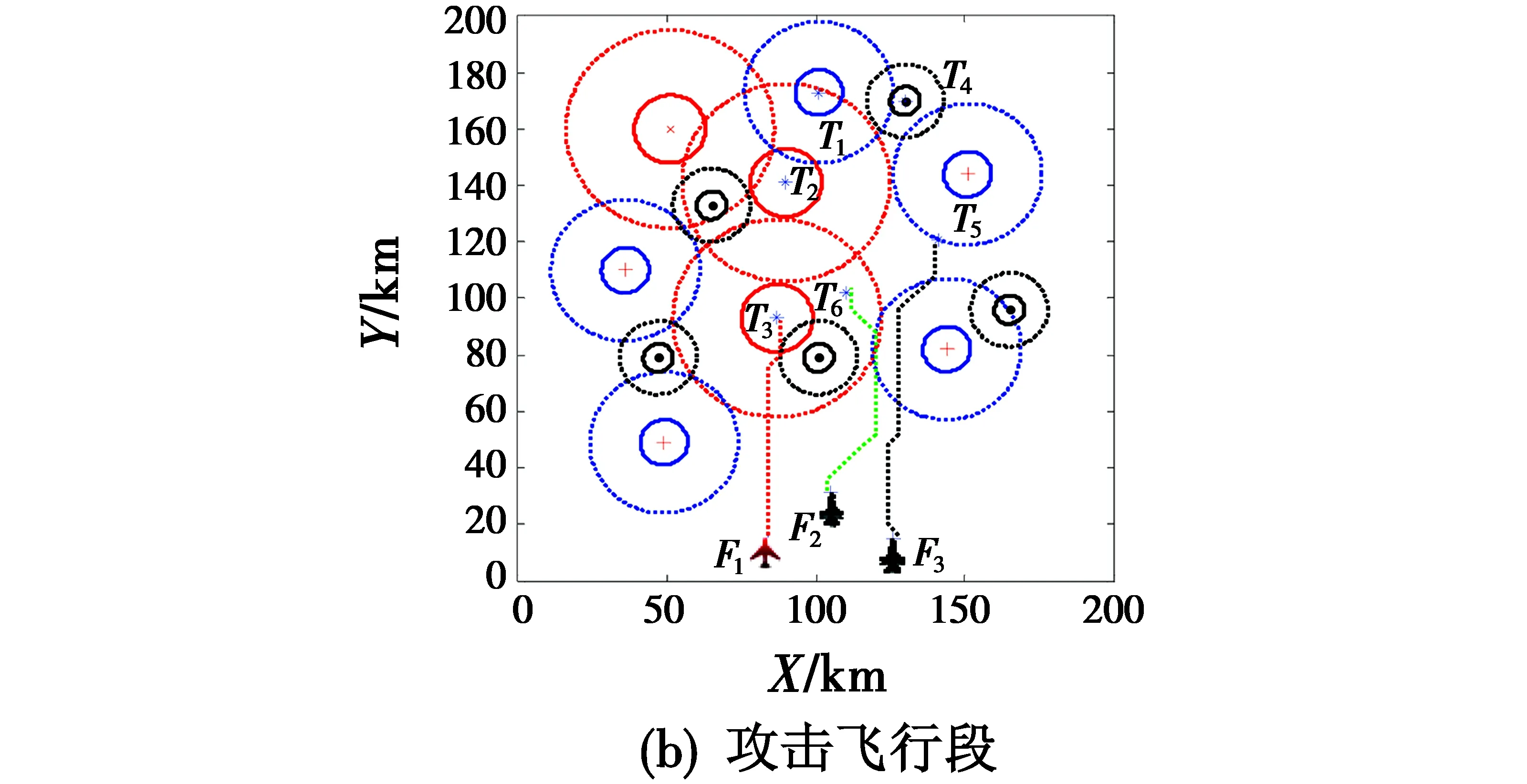
图5 第一阶段编队飞行航路Fig.5 The first stage formation flight route
在第一阶段,战机F1对目标T3实施电子干扰,掩护战机F2对目标T6实施打击,当战机F1抵达雷达T3探测边缘对其实施电子干扰时,战机F2并未进入雷达T3的探测范围,满足编队攻击时间协同约束。
编队内各战机完成第一阶段攻击任务后,遂转入第二阶段攻击,重置各战机目标航路点与初始航路点进行第二阶段攻击航路规划。图6所示为第二阶段编队飞行航路。根据目标分配结果,第二阶段攻击中,战机F1对雷达T2实施电子干扰,掩护战机F2对目标T1实施攻击,目标T4距离雷达T2相对较远,战机F3攻击航路不会受到其威胁。通过上述分析,为满足编队对地攻击时间协同约束,需对战机F2参照目标T2与T1的位置信息重新设置动态协同引导因子。
图6 第二阶段编队飞行航路Fig.6 The second stage formation flight route
在第二阶段,编队掩护飞行航路段没有出现航路交叉情况,满足编队航路空间协同约束。战机F1抵达攻击雷达T2干扰点时,战机F2尚未进入雷达T2的威胁区域,满足编队攻击协同时间约束。
4 结束语
本文主要研究随队支援干扰编队协同攻击航路规划的时空约束问题。首先,对编队软硬杀伤协同攻击航路的协同约束条件进行分析建模;其次,根据战场威胁模型确立了单机航路规划代价函数,并设计了面向攻击时序约束的多机航路综合评价函数;最后,基于多子群协同进化蚁群算法引入相异种群信息素互斥机制避免编队航线交叉,为增强算法搜索效率,设计了动态目标引导因子。仿真结果表明,本文提出的算法具有较好的收敛性,能有效解决编队协同攻击航路规划的时空约束问题。
