基于V形钝体的压电能量采集器建模与实验研究

高斯杰，韩 东，郑明瑞，李世瑞，何纬峰，王瑾程，汪 胜，周天昊

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

0 引言

管道监控设备是管道运输安全的重要保障，稳定持续的供电是管道监控的必要需求[1]。压电能量采集器(简称PEH，Piezoelectric Energy Harvester)能够将流致振动的能量转化为电能，为能耗低的无线传感器及微机系统等供电，通过收集周围环境中的振动能或运输管道内流体流动的能量，可为管道监控设备的自供电提供可能性[2]。

涡激振动和疾驰是常被压电能量采集器利用的两种流致振动形式。其中，由于涡激振动的自限制特点，使得基于涡激振动的能量采集器对于工作环境要求较高，且获能效率存在局限性。而驰振的振幅会随着流速的增大而增大，更有利于压电能量采集器捕获能量[3]。目前，已经有许多研究者对基于驰振的压电能量采集器进行了研究，并且研究内容也较为丰富。在理论方面，Abdelkefi[4]提出一种基于欧拉-伯努利梁假设的分布参数模型，并研究了不同截面形状的尖端钝体对于压电能量采集器输出功率的影响；Sun[5]进行了类似的工作，并通过机电解耦简化了机电耦合方程的求解。而为了更加精准的预测能量采集器的性能，许多影响因素被研究者们所关注，例如几何线性[6]、温度[7]以及气动力近似模型[8-9]等。在性能优化方面，许多研究的优化方案在于改变摆动钝体的结构来提升压电能量采集器性能[10-13]。此外，通过放置干扰柱[14]以及在能量采集系统中引入非线性力(如磁力[15])也能有效降低压电能量采集器的起振速度，提高其工作性能。Tan[16]还考虑了外部电路对压电能量采集器的性能影响，通过设计外部RLC电路提高了压电能量采集器的输出功率。

通过以上文献综述可以发现，对于基于驰振的压电能量采集器而言，提高尖端钝体所受的驰振力，从而增加系统的能量输入，这是增加这类发电系统功率输出的重要途径。因此本文提出一种新型的钝体结构，以增强尖端的驰振响应。通过准稳态假设得到其驰振力，在现有压电能量采集器分布参数模型的基础上推导出对应的分布参数模型。通过实验验证数学模型的合理性，并利用数学模型研究不同物理参数对压电能量采集器性能的影响。

1 数学模型

本文所研究的压电能量采集器由尖端钝体、悬臂梁及压电纤维片组成，压电纤维片贴于悬臂梁一侧的表面，悬臂梁的自由端与钝体相连，压电能量采集器结构示意图如图1(a)所示。图1(b)展示了能量采集器的结构尺寸，其中来流方向垂直于钝体的轴线方向，钝体会在流体的作用下带动悬臂梁沿y方向周期性摆动，此过程中产生的振动能量通过压电片转换为电能。

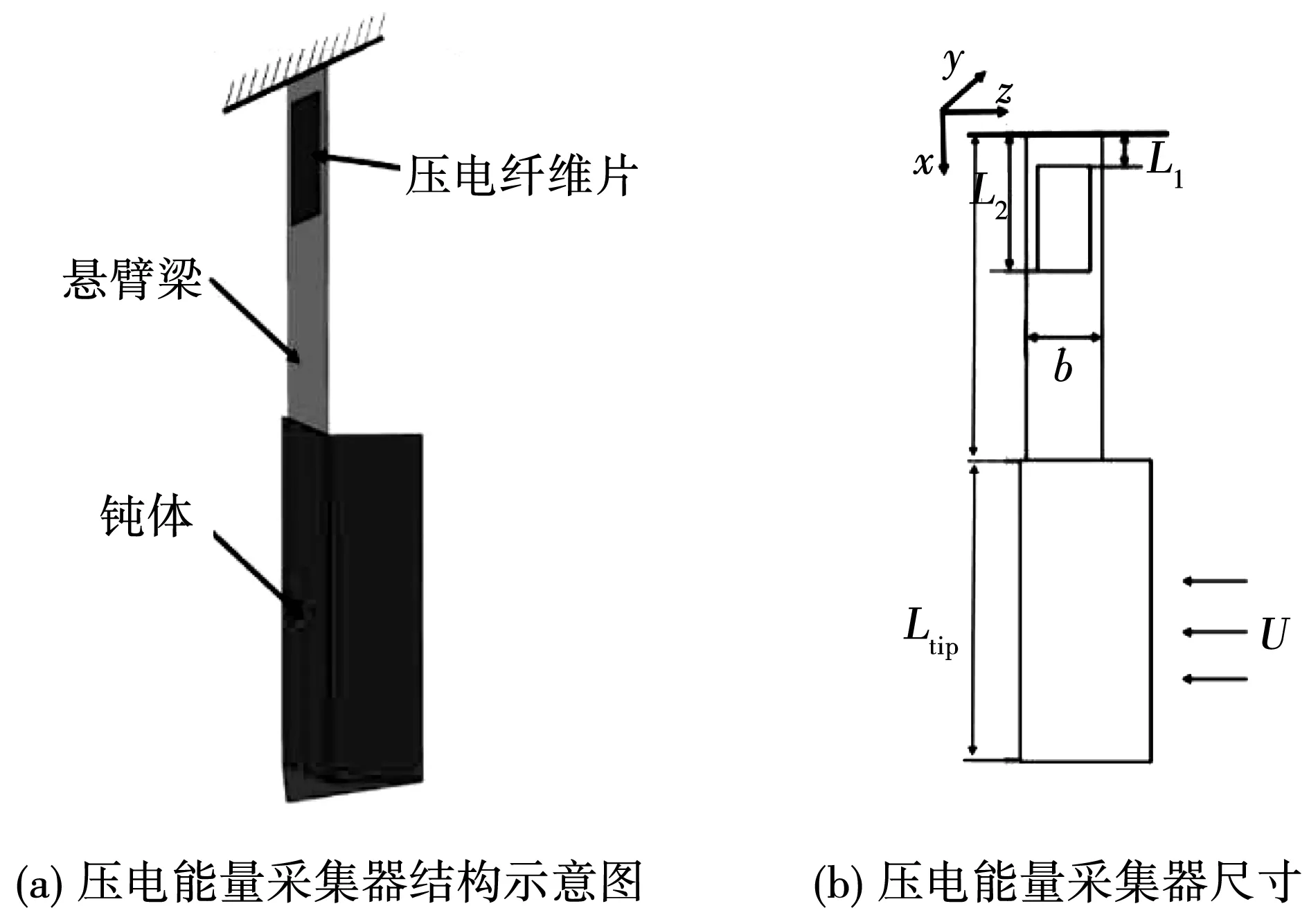
图1 压电能量采集器示意图

对这种压电能量采集器而言，基于Euler-Bernoulli梁假设和哈密顿原理得到其机械控制方程为[17]

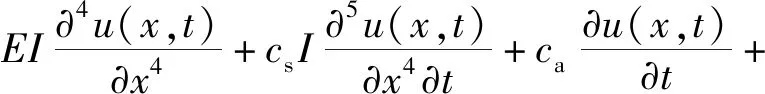
(1)

式中EI——悬臂梁的刚度;

m——悬臂梁单位长度的质量。

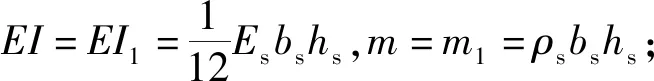
通过高斯定律[18]建立能量采集器的机械运动与电能生成之间的关系，电控方程表示为

(2)

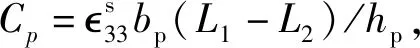
钝体所受的驰振力Ftip与力矩Mtip表示为

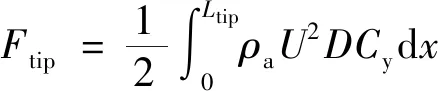
(3)

基于准稳态假设，得到驰振力系数在y方向的分量

Cy=a1tanα+a3(tanα)

(4)

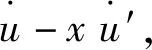
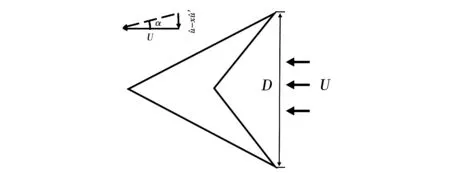
图2 V形钝体截面示意图

(5)

因此，悬臂梁自由端所受的气动驰振力和力矩可改写为

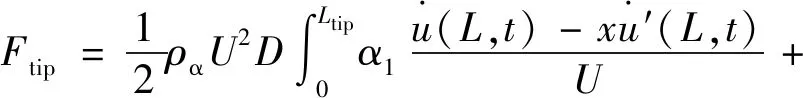
(6)

通过降阶处理[19]，可得到压电能量采集器的机电控制方程为

(7)

式中ξ——机械阻尼系数；

ω——能量采集系统的固有频率；

θp——压电耦合系数，θp=[φ′(L2)-φ′(L1)]ϑp;

φ(x)——悬臂梁的一阶振型函数；

q(t)——模态坐标；

f(t)——气动力项，表示为

(8)

式中k1、k3由下式给出

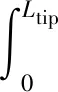
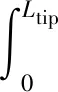
(9)

通过求解式(7)得到能量采集器的电压响应V(t)，功率由电压的均方根计算得出，即

(10)

2 实验研究

为了验证数学模型的正确性，用图3所示的实验系统进行了压电能量采集器的风洞实验。能量采集器的悬臂梁材质为65锰钢。压电点纤维片型号为M-2814-P2，用环氧树脂胶粘于悬臂梁表面。悬臂梁自由端连接V形钝体，使得钝体迎风面与风道来流风速垂直。

图3 实验布置

压电纤维片通过导线与外部负载连接，并使用示波器(DSO5102P，Hantek)采集电压信号。实验中使用的实验件的物性参数与几何参数由表1给出，外接负载阻值为105Ω，测试风速为0～8.5 m/s，风速间隔为0.5 m/s。

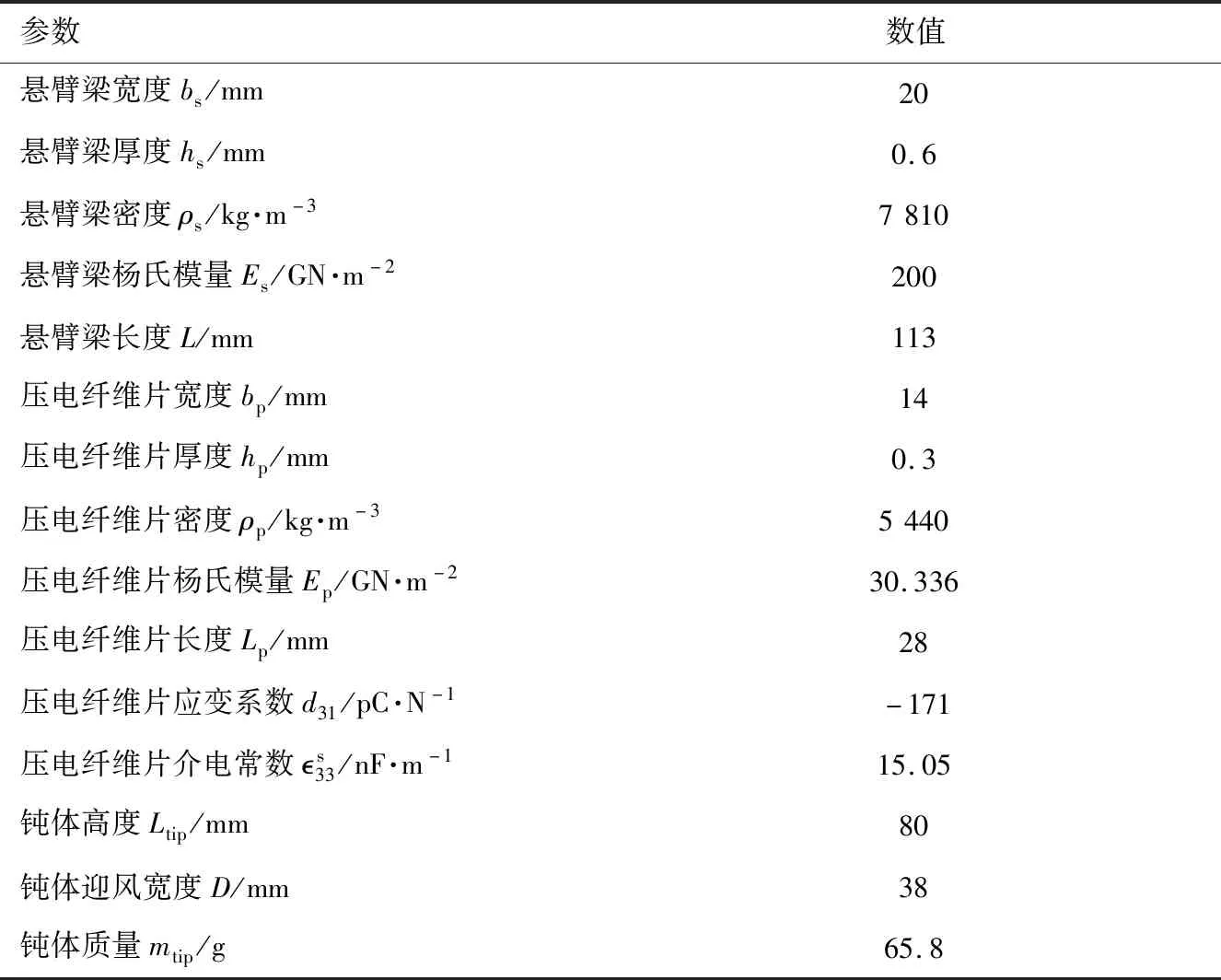
表1 压电能量采集器的物性参数与几何参数

3 结果与分析

3.1 模型验证

图4是实验中测得的能量采集器功率和数学模型预测的输出功率随风速变化的曲线，数学模型中使用的V形钝体的气动经验参数a1和a3分别为2.868和-81.3363。在实验方面，当风速超过2.0 m/s时，能量采集器尖端钝体出现明显振动，输出功率开始明显增大，且随着风速的增加，输出功率逐渐增大，当风速达到8.5 m/s时，输出功率达到最大值0.729 7 MW，实验现象与驰振现象的表现相符。而对于数学模型，通过对式(7)线性分析[4]得到该压电能量采集器的起振风速为2.68 m/s，在风速为8.5 m/s时，输出功率为0.689 9 MW，数学模型的输出功率解析解与实验值吻合良好。

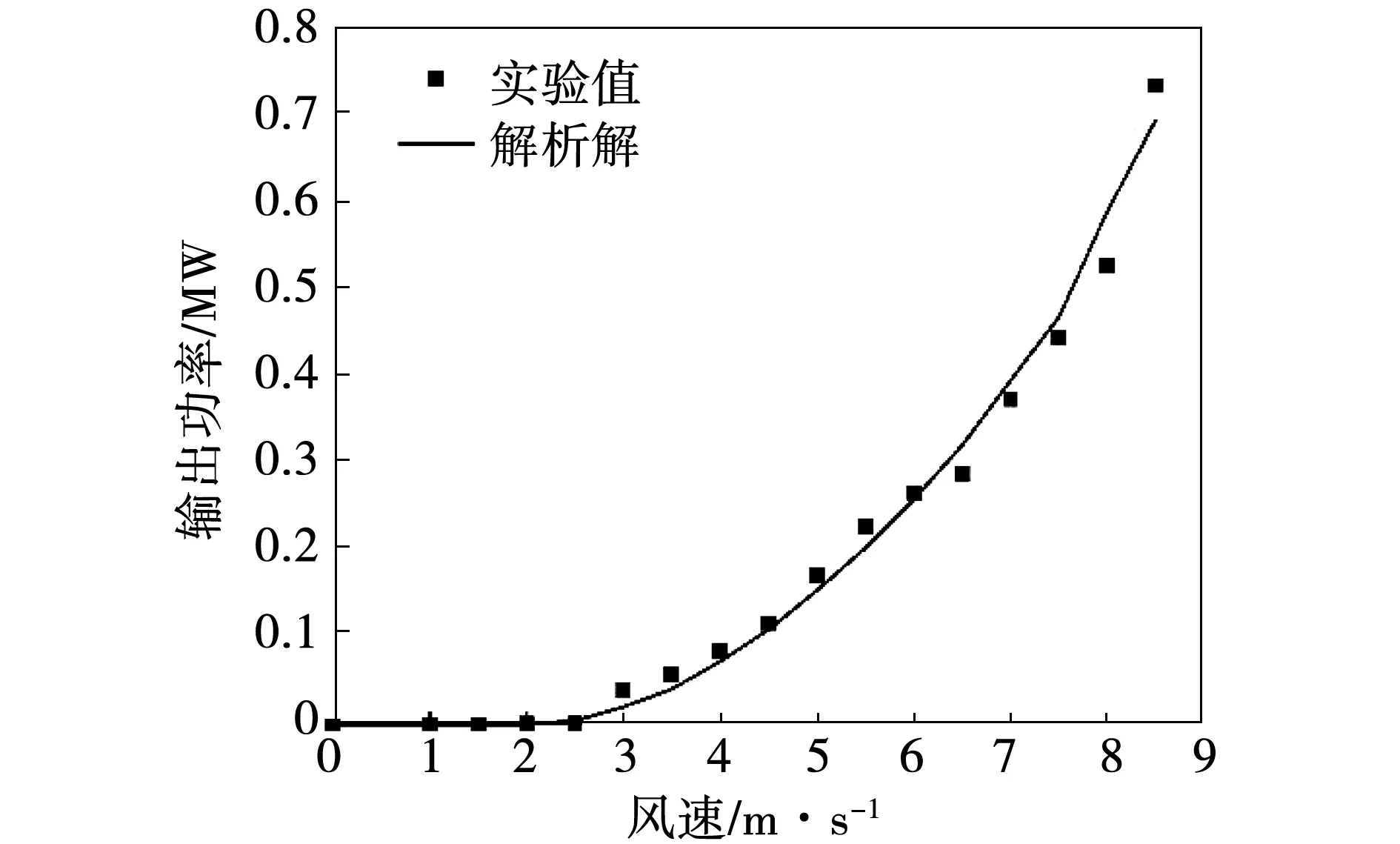
图4 能量采集器输出功率实验值与解析解对比

为了更加展示V形截面钝体能量采集上的优势，本文选取了Zhao[20]的研究进行对比，其所研究开设了V形槽的方柱与本文研究的V形截面钝体具有一定的相似性。通过对比相同工况下的输出功率可以发现，电能量采集器在8 m/s风速下的功率密度为0.38 MW/cm3，而本文实验中的压电能量采集器在同工况下的功率密度为0.44 MW/cm3，说明本文所设计的V形截面的尖端钝体能在驰振中更好的收集能量。

3.2 性能预测

根据建立的压电能量采集器数学模型，分析钝体质量、高度以及流速和负载对压电能量采集器的起振速度及输出功率的影响。

图5展示了不同风速下压电能量采集器输出功率随负载阻值的变化，流速为8 m/s、10 m/s、15 m/s和20 m/s。可以看到，压电能量采集器的输出功率随着风速的增加而增加。而对于不同的负载，输出功率随着负载阻值的增加会先增大后减小。在阻值较小(R≤ 104Ω)和较大(R≥ 104Ω)时，输出功率相对平稳，且输出量较小。当阻值大于104Ω时，压电能量采集器的输出功率开始急剧变化，且在1.5×106Ω附近不同风速下的压电能量采集器都取得最大功率，即压电能量采集器的最佳负载为1.5×106Ω。

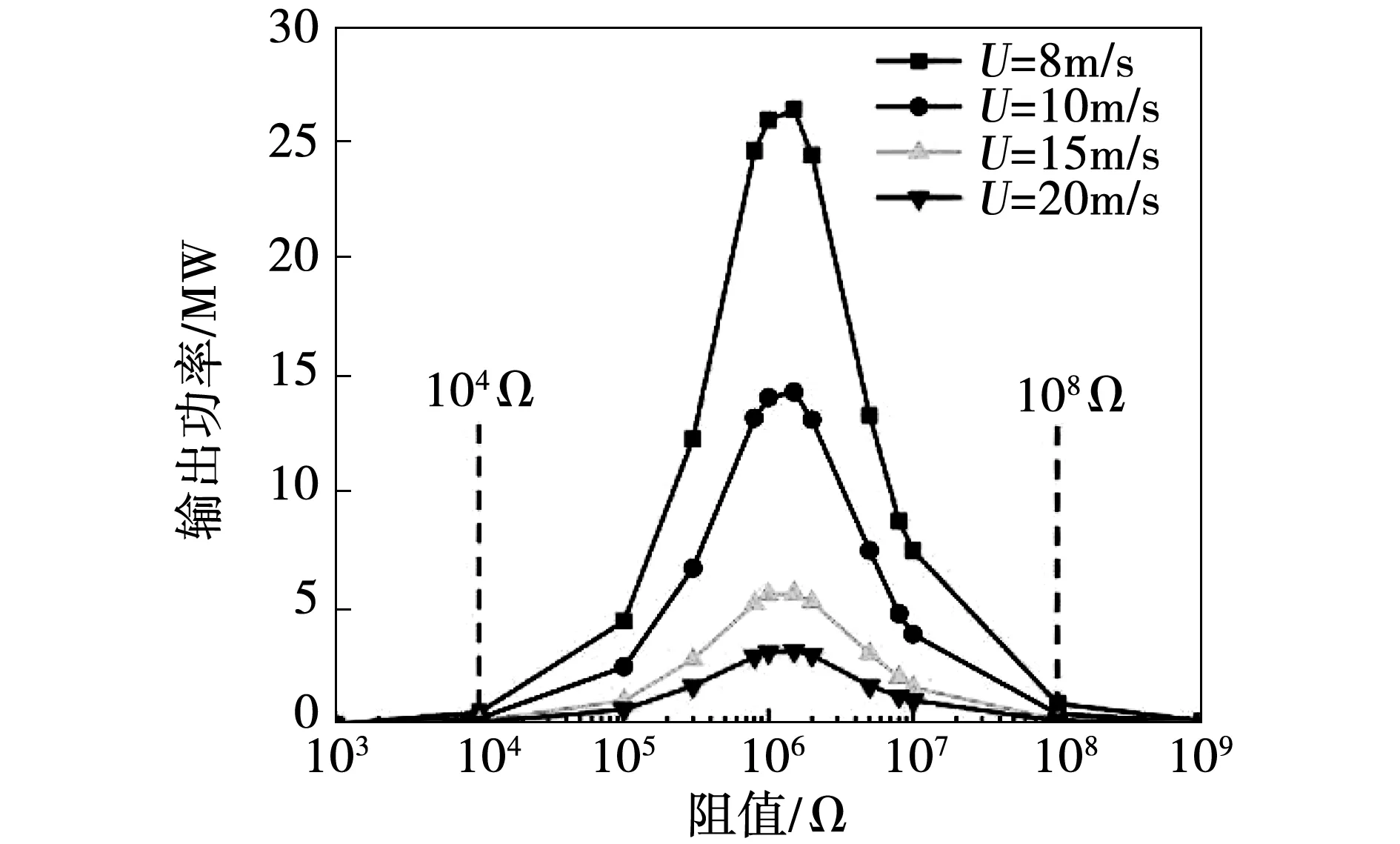
图5 不同风速下能量采集器输出功率随负载阻值的变化

图6为不同钝体高度下负载对压电能量采集器起振速度和输出功率的影响，钝体高度为80 mm、100 mm、120 mm和140 mm。从图6(a)中可以看到，随着负载阻值的增加，压电能量采集器的起振风速先增加后降低，说明负载会影响发电系统的总阻尼，并且最大起振风速对应的负载阻值与最佳负载阻值相近，说明当发电系统的输出功率达到最佳的同时总阻尼也达到较大值，因此需要更大的驰振力来克服阻尼，使得起振风速增大。从钝体高度来看，压电能量采集器的起振速度随钝体高度的增加而降低。对输出功率而言，如图6(b)所示，在最佳阻值前(R≤1.5×106Ω)，输出功率随着钝体高度的增加而降低；而当R=1.5×106Ω时，输出功率随着钝体高度的增加先增加后减小，即存在一个最佳的钝体高度会使压电能量采集器的输出功率最大化，在考虑的钝体高度范围内，在钝体高度为Ltip=100 mm时取得最大值3.129 MW；当阻值更大时(R≥3×106Ω)，钝体高度对输出功率的影响变小，不同高度下的输出功率基本相同。

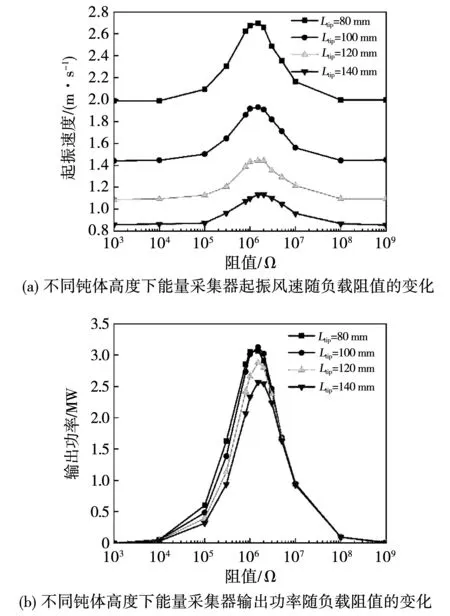
图6 钝体高度对压电能量采集器的影响

图7是不同钝体质量下压电能量采集器起振速度和输出功率随负载的变化。从图7(a)中可以看出，压电能量采集器的起振速度随钝体质量的增大而增大，这是因为钝体质量的增加使得发电系统的惯性增强，因此需要更大的驰振力使发电系统起振。此外，对于不同质量的钝体而言，其最大起振速度对应的阻值也随着钝体质量的增大而增加。在输出功率方面，如图7(b)所示，对于最大输出功率而言，钝体质量对最大输出功率的影响与钝体高度类似，最大输出功率随着钝体质量的增大先增加后降低，在所考虑的钝体质量范围内，当钝体质量为90 g时，取得最大输出功率3.335 MW。

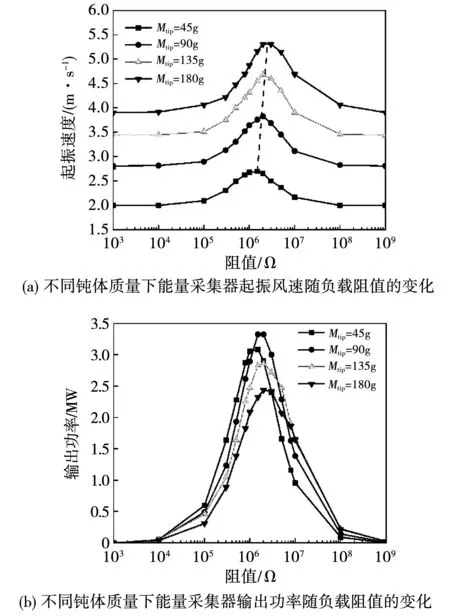
图7 钝体质量对压电能量采集器的影响

4 结论

本文研究了一种采用V型截面的钝体的悬臂梁式验电能量采集器，通过准稳态假设建立了其分布参数模型。通过风洞实验验证了该模型的准确性，实验结果与其他相似研究对比发现V形截面钝体在能量采集方面更具优势。利用模型计算了风速、外部负载以及尖端钝体质量和高度对能量采集器的性能影响，分析发现：能量采集器的输出功率随风速的增加而增加；起振风速随钝体高度的增加而降低，随钝体质量的增加而增加；存在最佳外部负载、钝体高度和钝体质量使得能量采集器的输出功率最大。