重载铁路基床污染级配碎石临界动应力及动强度特性研究

杨志浩，岳祖润，叶朝良，胡田飞，介少龙

(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043；2.石家庄铁道大学 河北省交通工程结构力学行为演变与控制重点实验室，河北 石家庄 050043；3.石家庄铁道大学 交通运输学院，河北 石家庄 050043)

重载铁路基床表层的级配碎石填料在长期运营过程中，由于外部灰尘的侵入、自身破碎及路基下部结构细颗粒的向上翻浆[1-2]，导致其受到不同程度的细颗粒侵入污染[3-4]，本文称其为污染级配碎石(Fouled Graded Macadam，FGM)。FGM较设计的级配碎石在渗透及力学特性方面发生较大变化，导致整个路基结构的工作状态大幅劣化[5]，大面积病害逐渐显现。土体的临界动应力及动强度对其在循环荷载下变形行为的演变起决定作用，故掌握FGM在大轴重循环荷载作用下的临界动应力及动强度演变规律，并建立相应的量化计算模型，对于揭示路基病害发生机理及灾害防控具有重要意义[6]。

较多学者结合动三轴试验，对多种路基填料的临界动应力进行了大量研究，并取得了丰硕成果[7-11]，主要研究了含水率[7]、围压[8]、初始固结应力[9]、密实度[10]及加载频率[11]等因素对试样临界动应力的影响规律，但大多数集中在黏土[8]、粉土[11]、黄土[7]及石灰/水泥改良土[12]等细颗粒土，而粗颗粒土由于试样大，试验仪器限制等原因，开展的研究仍不完善，尤其针对低围压、高循环应力比、高频率及大次数交通荷载作用下的规律更需深入研究。其中刘宝等[2]、王康宇等[13]、刘大鹏等[14]、孔祥辉等[15]、蔡袁强等[16]、周文权等[17]、冷伍明等[18]以粗颗粒土为研究对象，开展大型动三轴试验，表明试样的物理状态参数、应力历史及排水条件等因素与试样的变形形态及临界动应力间具有较好的相关性。而细粒含量作为粗粒土填料的重要物理状态表征参数，其对试样的变形行为及破坏规律具有显著影响[19]。但目前该方面的研究对象大多为污染道砟填料[3-4]，以FGM为对象的相关研究较少。且有学者认为随细粒含量的增大，试样临界动应力反而减小[4]，而也有学者认为随细粒含量增大，试样临界动应力相继增大[20]。可见，关于细粒含量对粗颗粒填料临界动应力的影响规律尚未得到共识，且细粒含量对重载铁路FGM变形行为及临界动应力的影响规律研究尚未见报道，仍需开展深入研究。

定性掌握细粒含量、围压、含水率等参数对FGM临界动应力的影响规律的同时，定量确定不同状态下FGM的临界动应力同样具有较大工程应用价值。但由于土体临界动应力的影响因素较多，对其进行理论计算较困难，故目前较多研究集中在多种因素对临界动应力的影响规律方面，针对定量计算模型的研究仍不完善。其中王康宇等[13]以最大粒径为20 mm的级配碎石为研究对象开展动三轴试验，提出了2种频率下临界动应力与围压的计算关系式；冷伍明等[21]、周文权等[17]针对A组填料开展动三轴试验，得到了临界动应力与含水率及围压间的函数关系。细粒含量作为重载铁路FGM的重要物理状态参数，建立考虑细粒含量参数的重载铁路FGM临界动应力计算模型对于路基安全性评估具有重要意义，需开展相关研究。

土体的静、动强度均与其物理状态及应力条件具有良好的相关性，故建立二者间的对应关系具有较强的可行性。众多学者也针对该内容展开了较多研究，刘建坤等[22]、杨庆等[23]及蒋关鲁等[24]均结合三轴试验建立了相应的计算模型，但研究对象仍然多集中在细颗粒土。重载铁路基床表层级配碎石填料较其他土工填料级配范围相对集中，建立其静、动强度间的换算模型具有重要的工程应用价值。

综上，为探究重载铁路基床表层FGM在大轴重循环荷载作用下的临界动应力及动强度的演变规律，首先，本文选取不同细粒含量(模拟不同污染程度)级配碎石填料，开展一系列不同条件下的大型动三轴试验，探索围压和细粒含量对该填料累积塑性应变及临界动应力的耦合影响机制。然后，基于塑性安定理论，对试样在不同条件下的变形行为进行划分，并进一步建立考虑细粒含量参数的FGM塑性蠕变状态临界动应力的计算模型。最后，结合试验数据，构建FGM静、动强度间的换算模型。研究成果为既有线重载铁路路基工后沉降预测及基于动强度控制的路基结构设计提供参考。

1 试验设计

1.1 试验仪器与土样

试验仪器采用STX-600型双向振动大型三轴仪，主要包括围压室、轴向作动器、加载架、液压泵、空气压缩机、围压/反压控制器、数据采集仪、移动导轨及计算机控制系统等。可施加轴向最大静荷载1 000 kN，轴向最大动荷载800 kN，最大围压2 MPa，最大加载频率20 Hz。本试验用土取自重载铁路某路基级配碎石施工填筑现场，经岩性测试可知其母岩为花岗岩。结合文献[19]定义细粒含量指标Fc，其计算式为

(1)

式中：ml、mg分别为粒径小于、大于0.075 mm颗粒的干质量，g。

收集整理重载铁路工务部门对基床表层级配碎石填料的维修资料可知，该填料的细粒含量一般为3%～10%，故本试验选取3种Fc指标分别为3%、5%、10%，并参照TB 10625—2017《重载铁路设计规范》[25]中关于基床表层级配碎石填料的级配要求，配制不同Fc指标的级配碎石土样。为模拟污染所掺加细粒土的液限为24.7%，塑限为16.3%，黏粒含量为11.4%。结合其级配特征及物性指标，可知该细颗粒为粉土。3种Fc指标级配碎石土样及细颗粒粉土的级配曲线见图1，物理力学性能参数见表1。

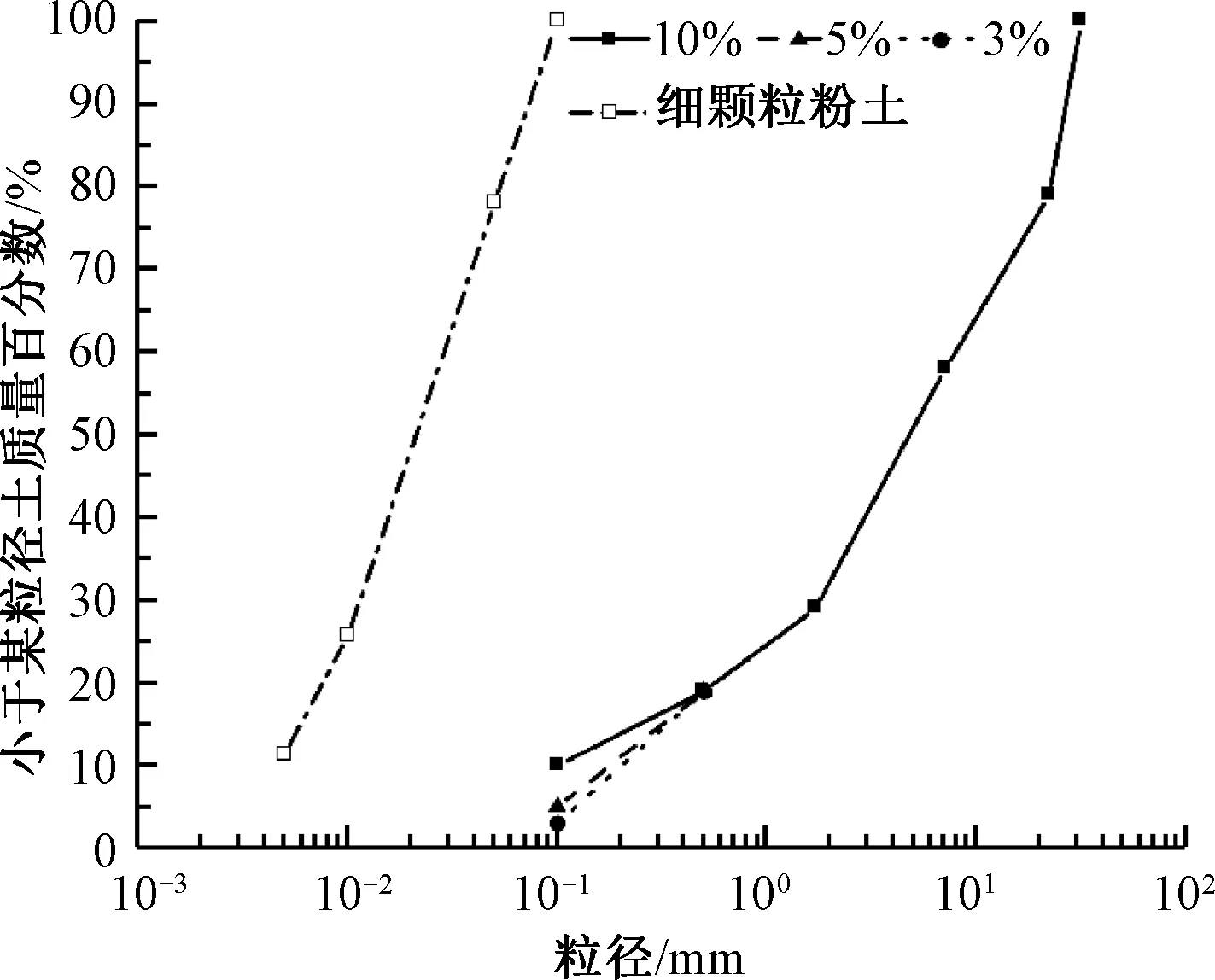
图1 试验所用土料的粒径级配曲线

表1 FGM 3种不同Fc的物理力学性能参数

试样尺寸为Φ300 mm×600 mm，试样直径为最大颗粒粒径的9.5倍，满足尺寸效应的要求[26]。本试验模拟运营路基基床级配碎石含水率不变时，受到细颗粒侵入污染的实际工况，故制备试样时设计为同一含水率(6%)，近似为最优含水率，以模拟该填料在最优工作状态下受到细颗粒侵入污染的工况。压实系数参照规范选取0.97，三轴试验操作流程参照SL 237—1999《土工试验规程》[26]及TB 10102—2010《铁路工程土工试验规程》[27]执行。

1.2 试验方案

试验形式为固结不排水，试验中对试样的轴向加载方式见图2。其中，AB段为围压施加阶段，用σ3表示，结合文献[18]，设计3个围压值15、30、60 kPa。BC段为各向等压固结阶段。CD段为上部轨道结构的静荷载σs，针对重载铁路基床表层的埋深，参考文献[8,20]并结合朗肯土压力公式进行估算，选取为15 kPa。DE段为循环加载阶段，加载波形为正弦形式，加载频率结合车速为100 km/h的C80型重载车辆经过路基的主频进行设置，选取为2.5 Hz。动应力幅值为σamp,d为循环加载阶段最大动应力σmax,d及最小动应力σmin,d的差值。由于本试验欲对FGM的临界动应力及动强度特性进行研究，故有意增大σamp,d设计。参照文献[17]，采用先分级50 kPa后分级25 kPa的原则，并依据每一次试验结束后试样轴向累积塑性应变与振次间关系曲线的发展形态来进行后续试验动应力幅值参数的设计。最终σamp,d的最大值选为525 kPa，所有动三轴试验设计参数见表2。参照文献[17-18]，选取试验破坏标准为轴向累积塑性应变εsd达到15%，稳定标准为εsd<5%[28-29]，且1 h内εsd增量小于0.2%。前期预试验表明，振动40 000次可满足本文对于FGM临界动应力及动强度特性的研究目的，故各试验统一设定最大振次为40 000次。试验过程中严格控制试验细节，尽量消除人为误差，且每种试验工况均设计2～3组平行试验，以验证试验数据的可靠性。

图2 动三轴试验轴向加载方式

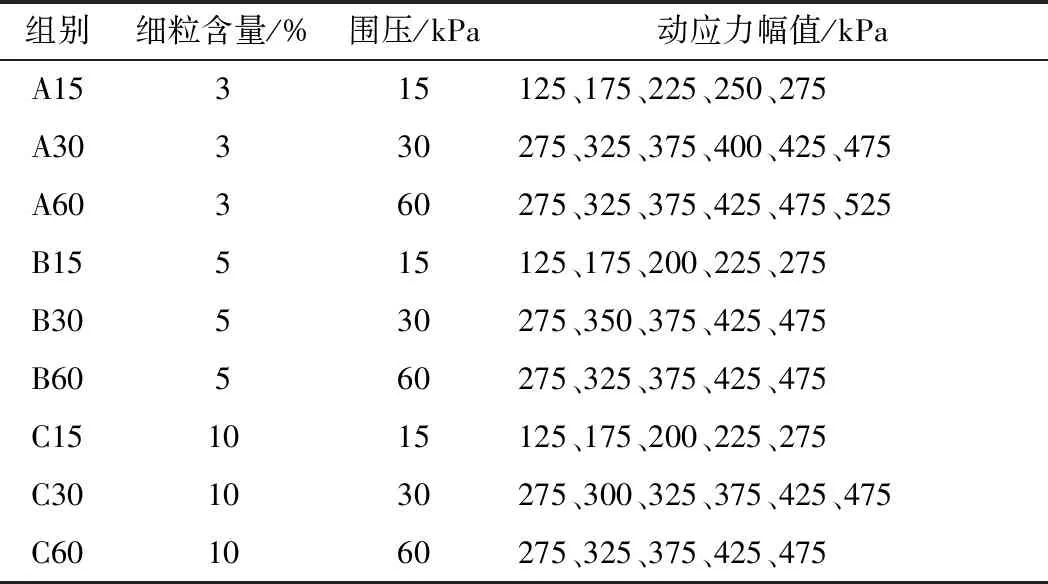
表2 动三轴试验设计参数

2 试验结果与分析

2.1 试样变形形态分析

结合塑性安定理论[6]，可将试验结束后的试样变形形态分为3种，见图3。由图3(a)可知，宏观表现为试验结束后试样的εsd<4%，且试样无明显外鼓变形，拆除橡胶膜后内部颗粒连续性好。由于该幅值荷载作用下，加载初期试样内部发生颗粒棱角的剪切破碎，εsd快速增长。但加载至某一振次时，试样内部颗粒间棱角剪切破碎发育完全，且试样足以抵抗该幅值荷载的作用，故后续加载过程中试样处于弹性状态，仅发生弹性应变，无塑性应变产生，即εsd趋于稳定状态，且值较小。

由图3(b)可知，宏观表现为试验结束后试样εsd>4%，但小于破坏应变15%，具有明显外鼓变形，试样剪切破坏面较明显，与试样高度方向夹角约45°。由于该幅值荷载作用下，试样强度不足以抵抗该荷载的作用。加载初期试样内部颗粒间棱角破碎的同时，也发生相对滑移，导致试样变形快速增长。但随着变形的增大，试样被压密，导致试样强度增大，抵抗外部荷载作用的能力增强，但仍不足以抵抗该幅值荷载的作用，故随加载次数的持续增大，试样始终有塑性应变的累积。但随着试样强度的增大，εsd增长速率相继减小，最终在振动加载40 000次时的εsd仍小于破坏应变15%。

由图3(c)可知，宏观表现为试验结束后试样的εsd大于破坏应变15%，试样具有非常明显外鼓变形，可明显看出颗粒间较大相对滑移。由于该幅值荷载作用下，试样强度远远不足以抵抗该荷载的作用，导致试样εsd快速增长，并在较小振次达到破坏应变15%，最终试样破坏。

图3 试验结束后的试样形态

2.2 不同应力水平下的εsd-N曲线

对试验数据进行整理，绘制Fc=3%、5%、10%试样在不同应力水平条件下的εsd与振次N关系曲线，见图4～图6。

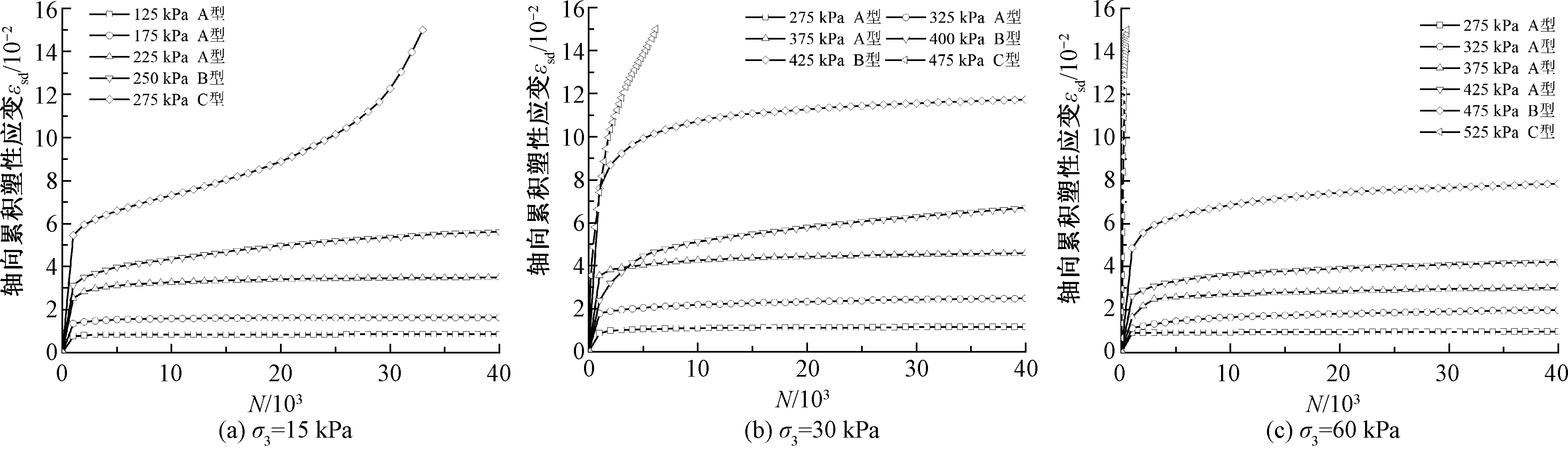
图4 Fc=3%试样εsd-N变化曲线

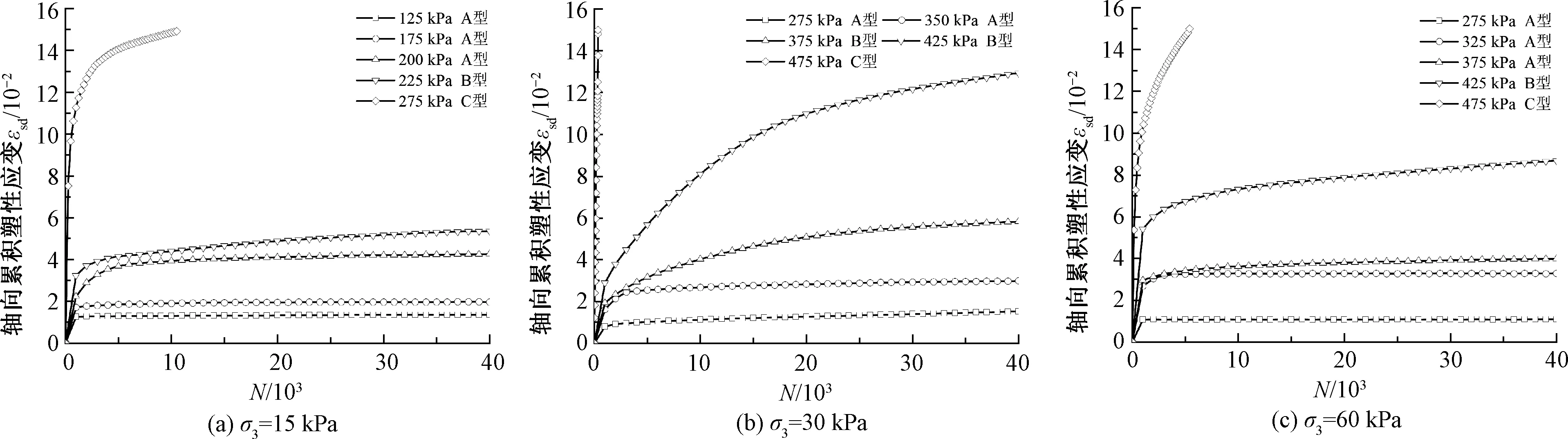
图5 Fc=5%试样εsd-N变化曲线

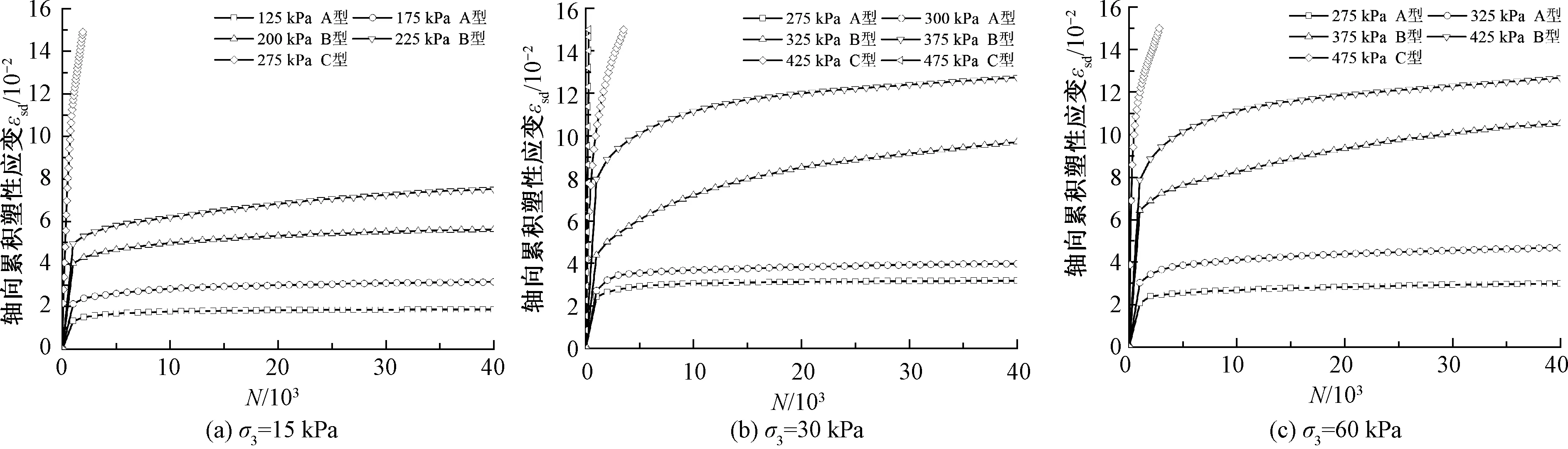
图6 Fc=10%试样εsd-N变化曲线

由图4～图6可知，不同应力水平下试样的εsd-N曲线发展规律明显不同，与图3试样变形形态相对应，分别为A型(塑性安定型)、B型(塑性蠕变型)及C型(增量破坏型)。

由图6(b)可知，对不同σamp,d条件下εsd-N曲线的演变规律进行分析。当σamp,d=275、300 kPa时，加载初期试样内部颗粒间咬合棱角破碎，试样εsd迅速增长。荷载继续施加，试样内部颗粒间棱角磨碎发育完全，最终在2 000振次内试样εsd趋于稳定，随后试样处于弹性稳定状态，没有塑性应变累积，最终在40 000振次时的εsd分别为3.18%、3.98%。当σamp,d=325、375 kPa时，加载初期试样内颗粒间咬合棱角破碎的同时，发生较大的相对滑移，导致εsd快速增长。变形的同时试样强度相继增大，但此时试样仍不足以抵抗当前荷载的作用，试样始终处于塑性状态，始终有塑性应变的产生。但由于试样强度逐渐增大，εsd增长速率减缓，并在40 000振次时的εsd分别为6.7%、9.7%、12.75%。当σamp,d=425、475 kPa时，试样强度远远不足以抵抗当前幅值荷载的作用，导致εsd快速增长，并在较小振次(3 520、291)达到破坏应变15%。

2.3 σ3、Fc对εsd的影响规律

为分析σ3及Fc对试样εsd的耦合影响规律，选取3种Fc指标下，σ3=15 kPa，σamp,d=225 kPa；σ3=30 kPa，σamp,d=375、425 kPa；σ3=60 kPa，σamp,d=375、425 kPa条件下试样在振动40 000次的εsd值进行分析，5种应力条件下的εsd与Fc的关系曲线，见图7。

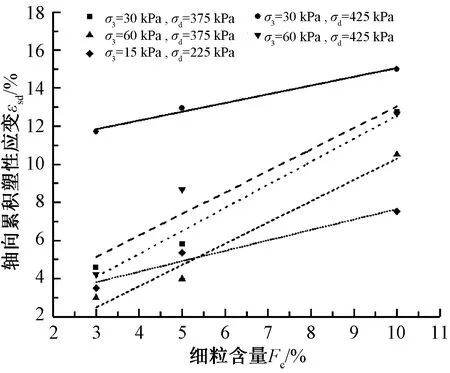
图7 振动40 000次εsd与Fc关系曲线

由图7可知，其他条件相同，随σ3增大或σamp,d减小，试样εsd相继减小。其他条件相同，随Fc增大，试样εsd显著增大。首先，细颗粒的增多对试样内部颗粒间的的嵌挤、咬合作用起到一定的润滑作用。其次，随Fc增大，试样的渗透特性降低，导致试样在加载过程中产生的超静孔隙水压力不易消散，试样受到的动有效应力增大，强度降低。上述两个作用均导致试样变形的增大，宏观上表现为εsd增大。

2.4 σ3、Fc对临界动应力的影响规律

为分析σ3及Fc对临界动应力σdcr的影响规律，结合文献[21]，定义循环应力比CSR为

(2)

结合试验参数表2及图4～图6中试样变形形态，绘制不同CSR与σ3条件下试样变形形态分布，见图8。

由图8可知，其他条件相同时，随σ3增大，试样的临界循环应力比CSRcr减小，且围压越小，变化越显著。不同σ3及Fc条件下，随CSR增大，试样的变形形态由塑性安定型经塑性蠕变型向增量破坏型逐步过渡。某一围压下均存在一塑性蠕变状态临界循环应力比CSRcr,pc及增量破坏状态临界循环应力比CSRcr,if，且3个σ3条件下的CSRcr与σ3间具有很好的相关性。由于路基结构设计的安全性，实际运营过程中出现列车在路基中产生的动应力大于其增量破坏状态临界动应力σdcr,if的概率很小，故仅对塑性蠕变状态临界动应力σdcr,pc的演变规律进行分析。结合文献[21]可知，CSRcr与σ3呈幂函数关系，故本文采用幂函数形式对3种Fc指标级配碎石的塑性蠕变状态临界循环应力比线进行拟合，3个拟合线的拟合优度R2均大于0.9，表明CSRcr,pc与σ3间具有很好的相关性。且随Fc增大，试样CSRcr,pc相继减小。表明随着细颗粒土的增多，试样的σdcr,pc减小。即当基床表层级配碎石填料受到细颗粒土的侵入污染后，在相同动应力的作用下可能由塑性安定状态过渡为塑性蠕变状态，进而在大次数循环荷载的作用下产生较大的累积变形，影响行车安全。

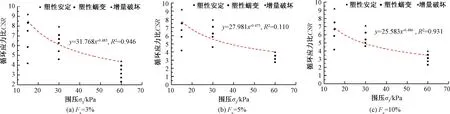
图8 3种Fc指标试样在不同应力水平下的动力行为分布

3种Fc指标试样塑性蠕变状态的临界循环应力比线表达式形式相同，且处于平行状态，故可在3个幂函数形式拟合公式基础上，结合Matlab，建立考虑Fc参数的FGM的CSRcr,pc表达式为

CSRcr,pc=50.567Fc-0.312×σ3-0.483

(3)

结合式(2)可得同时考虑σ3及Fc参数的FGM的σdcr,pc表达式为

σdcr,pc=101.134Fc-0.312×σ30.517

(4)

结合病害路基运营期间的整修资料，可知重载铁路基床表层FGM的Fc在3%～10%，则由式(4)也可看出，其他条件相同，随Fc增大，σdcr,pc减小；随σ3增大，σdcr,pc增大。经过验证，式(4)具有较高的准确性，应用该式可对既有重载铁路路基基床级配碎石填料的稳定状态进行评估。

2.5 动强度特性

掌握FGM临界动应力的演变规律，可为其是否发生破坏提供判据，但破坏试样中每个试样发生破坏的次数Nf不同，故需对该填料的动强度特性进行分析，进而探究Fc指标对该填料动强度的影响规律。在一定振动作用下，某一特定循环次数下使试样产生某一特定应变所对应的动应力值为动强度[18]。破坏振次越小，相应的动强度越大。破坏振次越大，相应的动强度越小。以σ3=30 kPa条件下3种Fc指标试样选取不同破坏应变时的动强度曲线，分析Fc对FGM动强度的影响规律，见图9。

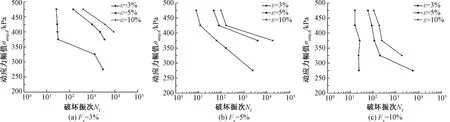
图9 3种Fc指标试样不同破坏应变的动强度曲线(σ3=30 kPa)

由图9可知，3种破坏应变条件下，随破坏振次的增大，所需要的动应力幅值越小，且随着动应力幅值的减小，试样的破坏振次变化幅度越大。表明FGM存在应力依赖性，即在较小幅值荷载作用下，相比大幅值荷载发生相同应变需要的循环作用次数显著增大。其他条件相同时，随Fc增大，试样的动强度曲线斜率越大。即在相同幅值动荷载作用下达到相同破坏应变，破坏振次随Fc增大而显著减小。表明重载铁路基床表层级配碎石填料受到细颗粒污染后，对动荷载作用的敏感性增强，易发生较大变形，故在路基基床表层的实际运营过程中应严格控制其填料的污染程度。建议铁路养护部门在路基养护过程中要定期检测基床表层级配碎石填料的细颗粒含量，当细颗粒含量超标时，要结合实际情况对该层填料进行换填。

由文献[18,23]可知，土体的静、动强度均主要由试样的初始结构来决定，故同等试验状态下试样的静、动强度间存在相关性。且为消除初始状态对试样动强度的影响，可将动应力幅值对同等状态下试样的静强度进行归一化，得到归一后动强度与破坏振次间的关系曲线。对表2中动三轴的Fc及σ3参数设计值，进行了3种Fc、3种σ3下的大型静三轴试验，并得到相应条件下的静强度值，见表3。

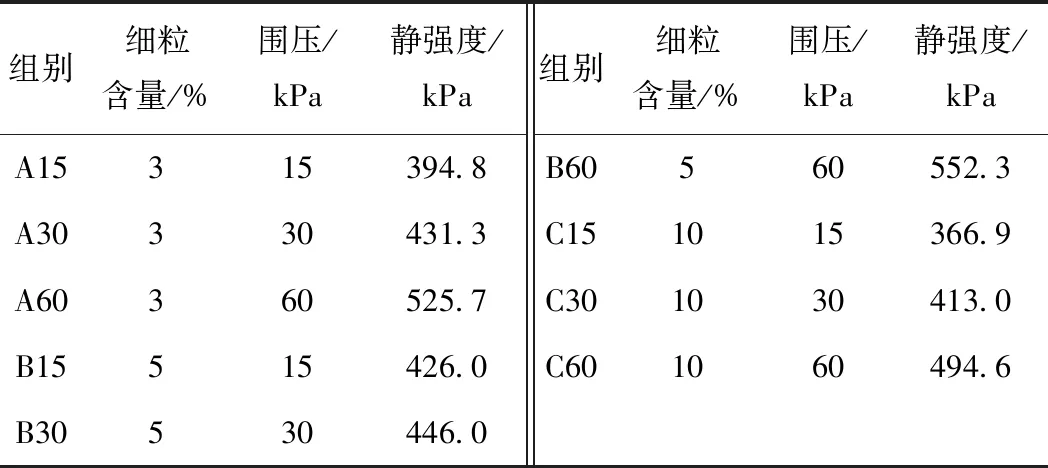
表3 不同条件下试样的静强度值

结合表2的动应力幅值参数及表3中的静强度值，可得到归一化动强度与破坏振次间的关系曲线见图10。由图10可知，归一化的动强度与破坏振次间存在良好相关性，本文分别进行了指数函数、幂函数及半对数函数形式的拟合计算，发现指数函数形式拟合程度好，拟合曲线方程为

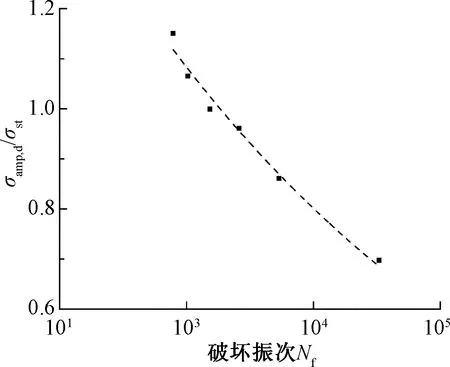
图10 归一化动强度曲线(ε=15%)

(5)

式中:σst为与该σamp,d动三轴试验相同条件下静三轴试验的静强度值，kPa；a、b为与试样物理状态有关的拟合参数，对于本试验所用的FGM填料，a=2.678 4，b=-0.131 1，拟合优度R2=0.983 3。

在获取静强度的同时，应用式(5)可进行一定设计年限条件下路基动强度的估算。亦可对一定动强度条件下路基的使用寿命进行估算。但需要说明，式(5)仅适用于TB 10625—2017《重载铁路设计规范》[25]中关于基床表层规定的级配碎石填料。若填料种类或级配发生改变，式(5)的准确性需进一步验证，但本文所用填料及其级配范围均为重载铁路基床表层施工现场最常见工况，对其进行研究仍具有重要意义。

3 结论

本文针对FGM开展一系列动三轴试验，对该填料的临界动应力及动强度特性进行探究，并建立了相应的塑性蠕变状态临界动应力计算模型及归一化动强度计算模型。主要结论有：

(1)FGM在不同应力水平循环荷载作用下表现出不同的变形形态，结合塑性安定理论，可将其分为塑性安定型、塑性蠕变型及增量破坏型。

(2)随围压增大或动应力幅值减小，试样累积塑性应变相继增大；其他条件相同时，细粒含量在3%～10%，随细粒含量增大，试样轴向累积塑性应变显著增大，且试样的临界动应力及动强度相应减小。表明重载铁路基床表层级配碎石受到细粒土的侵入污染后，可能由塑性安定状态转变为塑性蠕变状态，易产生塑性变形累积，影响行车安全。在实际运营过程中，应严格控制基床表层级配碎石填料的污染程度。

(3)本文提出的重载铁路基床表层FGM塑性蠕变状态临界动应力计算模型及归一化的动强度计算模型，具有较高准确性，可对重载铁路既有线路基安全评估及新线路基结构设计提供参考。