钢轨轨顶弯钩形滚动接触疲劳裂纹空间扩展特性研究

李骏鹏，周 宇，梁 旭，王 钲，卢哲超，程中宁

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室，上海 201804；3.中国铁道科学研究院集团有限公司 金属及化学研究所，北京 100081)

钢轨表面滚动接触疲劳裂纹及其引起的剥离掉块是影响铁路钢轨使用的主要问题之一[1]。随着合金和热处理等硬质钢轨在重载铁路的普遍使用[2]，钢轨滚动接触疲劳裂纹呈现萌生早、扩展快的特征[3]。对重载铁路小半径曲线钢轨表面裂纹跟踪观测发现，除在外轨和内轨轨距角-轨肩处有近平面状裂纹[4-5]之外，在内轨轨头顶面也出现大量疲劳裂纹并引起剥离掉块[6-7]。通过对内轨顶面取样和横、纵剖面观测，这类轨顶裂纹在剖面上呈现“弯钩形”走向[8](以下简称“弯钩形裂纹”)，其在扩展过程中路径会发生明显变化，从而在空间上呈现弯曲的形态。因此，需要合理分析这类裂纹的形成、扩展以及后续引起的剥离掉块问题。

针对钢轨滚动接触疲劳裂纹扩展研究，通常做法是在裂纹尖端分别建立一系列对于主裂纹无穷小的、不同方向的支裂纹，采用数值方法，如有限元法[9]、无网格伽辽金法[10]、边界元法[11]和扩展有限元[12]等进行裂纹扩展计算，并认为裂纹扩展方向为支裂纹最大的方向[13-15]。Pletz等[16]建立了二维准静态有限元模型研究车轮荷载下钢轨轨距角裂纹扩展；Li等[17]根据最大周向应力理论预测了轮轨疲劳加载下轨距角裂纹扩展方向；周宇等[18]在还原裂纹真实形态的基础上预测了轨距角斜裂纹扩展。大多数既有研究关注的是轨距角近平面状发展的斜裂纹，因此可将裂纹形态简化为平面半椭圆形或半圆形[19]，从而预测裂纹某一剖面在二维纵向平面内的扩展。轨顶弯钩形裂纹路径变化明显，不适宜将其简化为平面模型。常规的裂纹观测试验方法，如钢轨取样切片法[2,20]、金相分析法[21-22]等会破坏弯钩形裂纹的完整性[6,23]。因此，首先需要基于高精度无损检测技术，获取弯钩形裂纹的三维空间形态，建立相应的裂纹曲面模型，进而分析其在空间内的扩展特性。

本文从弯钩形裂纹的显微特征入手，基于X射线断层扫描技术[24]获得弯钩形裂纹三维真实形态，根据非均匀有理B样条方法(NURBS)[25-26]对弯钩形裂纹进行三维重构，提出裂纹不同扩展阶段的双曲面模型；考虑钢轨磨耗影响[1]，建立车辆移动荷载作用下裂纹空间扩展预测方法，计算裂纹尖端各点的应力强度因子，并研究弯钩形裂纹在空间上的扩展特征，为轨顶弯钩形裂纹研究和预测提供参考。

1 弯钩形裂纹扩展预测模型

1.1 轨顶面弯钩形裂纹三维重构

1.1.1 弯钩形裂纹显微分析

本文钢轨取样来自我国某重载铁路半径为500 m曲线内轨，为U75V离线热处理轨，取样时累积通过总重约100 MGT(百万t)，车辆轴重为23～30 t，列车速度为70～80 km/h，内轨取样长度约100 mm，轨肩-轨距角和轨顶面均有大量裂纹分布。内轨取样和显微观测试块见图1。按图1(a)的尺寸采用线切割方式、以轨距边为基准向内分别取宽度12、18 mm的试块，试块厚度为20 mm，长度50 mm以内，取样试块基本包含轨头表面裂纹，从而对中间试块横纵断面进行显微观测，见图1(b)、1(c)。

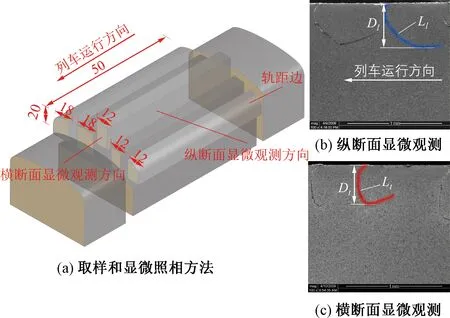
图1 内轨取样和显微观测试块(单位：mm)

从图1可以看出，轨顶中部试块浅层已出现弯钩形裂纹。进一步采用灰度图像识别[27]对裂纹及其母材进行区别，并沿其走向进行曲线拟合，从而得到图1(b)的纵断面上裂纹尺寸为：从表面开口至其尖端的拟合曲线长度Ll为1.23 mm、裂纹表面开口至裂纹最低处的垂直距离为裂纹深度Dl为0.48 mm；同理，图1(c)中横断面上裂纹长度Lt为0.92 mm，裂纹深度Dt为0.47 mm。对轨头所有试块横断面显微照片进行组合，如图2所示，可以判定，弯钩形裂纹主要出现在距离轨顶中心12 mm范围内，这个位置的裂纹在横纵断面上均呈“弯钩形”，轨头外侧角和轨距角的裂纹仍呈平面状走向。

图2 横断面不同位置典型裂纹状态

根据图1、图2中弯钩形裂纹在钢轨横纵断面的走向和位置，模拟弯钩状裂纹的空间形态，见图3。裂纹起始扩展方向与列车运行方向成锐角，扩展到一定深度后，弯钩形裂纹扩展路径发生逆转，向逆行车方向转向后朝轨顶面扩展，从而形成弯钩形裂纹。

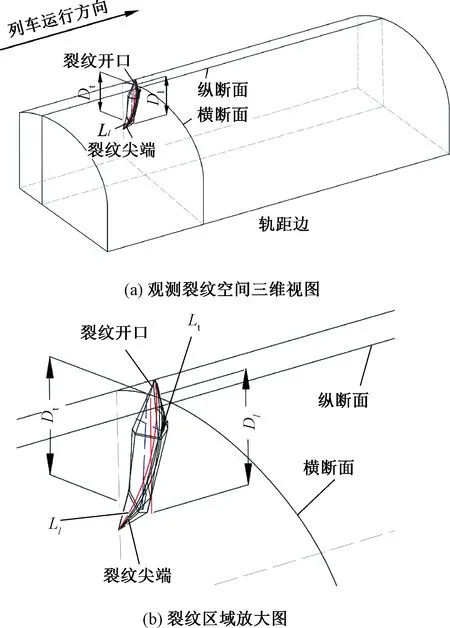
图3 通过总重100 MGT时弯钩形裂纹空间形态模拟

由图3观测可以发现，显微观测只能测量弯钩形裂纹在纵横断面上的投影，难以描述裂纹在空间中的真实形貌。为此，进一步引入X射线断层扫描技术(CT扫描)，测量弯钩形裂纹三维形貌并进行建模。

1.1.2 X射线断层扫描

X射线断层扫描装置包括180 kV/15 W纳米聚焦X射线管和解析度为3 072×2 400像素CCD照相机，具有200 nm的细节解析度、0.2 μm的分辨率，测试方法见图4。

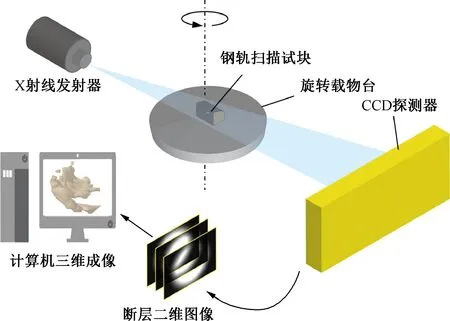
图4 X射线断层扫描含弯钩形裂纹的内轨试块

由于裂纹填充物成分主要是金属铁屑和粉尘，其密度略小于钢轨母材，经X射线照射后，穿过裂纹和钢轨母材的能量衰减不同。令任意一条X射线穿过钢轨试块，其入射强度为I0，穿过母材、裂纹等不同区域后，其强度衰减至I，则根据Lambert-Beer定律可得

I=I0·e-μ1·Δxe-μ2·Δxe-μ3·Δx…e-μn·Δx

(1)

式中：μi为材料衰减系数；Δx为物体厚度。

在扫描平面建立xy直角坐标系，令衰减系数分布为f(x,y)。则根据式(1)，射线在某一方向沿某一路径L的射线强度变化为

(2)

通过图像重建算法[28]重构裂纹二维平面图像，图像灰度值与钢轨试块衰减系数相对应。式(2)经取负对数后，记为P，表示射线穿透试块后的投影，可以通过测量得到，其物理意义为钢轨试块断面在X射线下的衰减系数沿直线L方向的线积分。

(3)

理论上X射线沿某一路径穿过被测物体，该路径可理解为一条直线，但试块断层是一个平面，平面内任意一点可用(x,y)表示，故可将该点理解为一很小的矩形区域，该矩形区域的衰减系数为f(x,y)。因此，穿过(x,y)的射线束投影可用P(x,y)表示

(4)

则根据X射线沿某一路径穿过断层的投影P(x,y)，可计算出扫描裂纹平面内每个点的衰减系数f(x,y),得到每个点的相对像素值，进而重建试块的二维图像，将二维图像层层堆栈，即可形成裂纹三维图像。

从图1和图2可见，相比弯钩形裂纹尺寸，显微照相的试块较厚较宽，影响CT扫描识别裂纹的精度。根据弯钩裂纹在轨顶的位置和范围，从而尽量保持弯钩裂纹完整的角度，设计切割方案，含弯钩形裂纹试块取样示意见图5。图5(a)中试块(2′)即为CT扫描试块，其尺寸为：长50 mm、宽25 mm、厚5 mm。

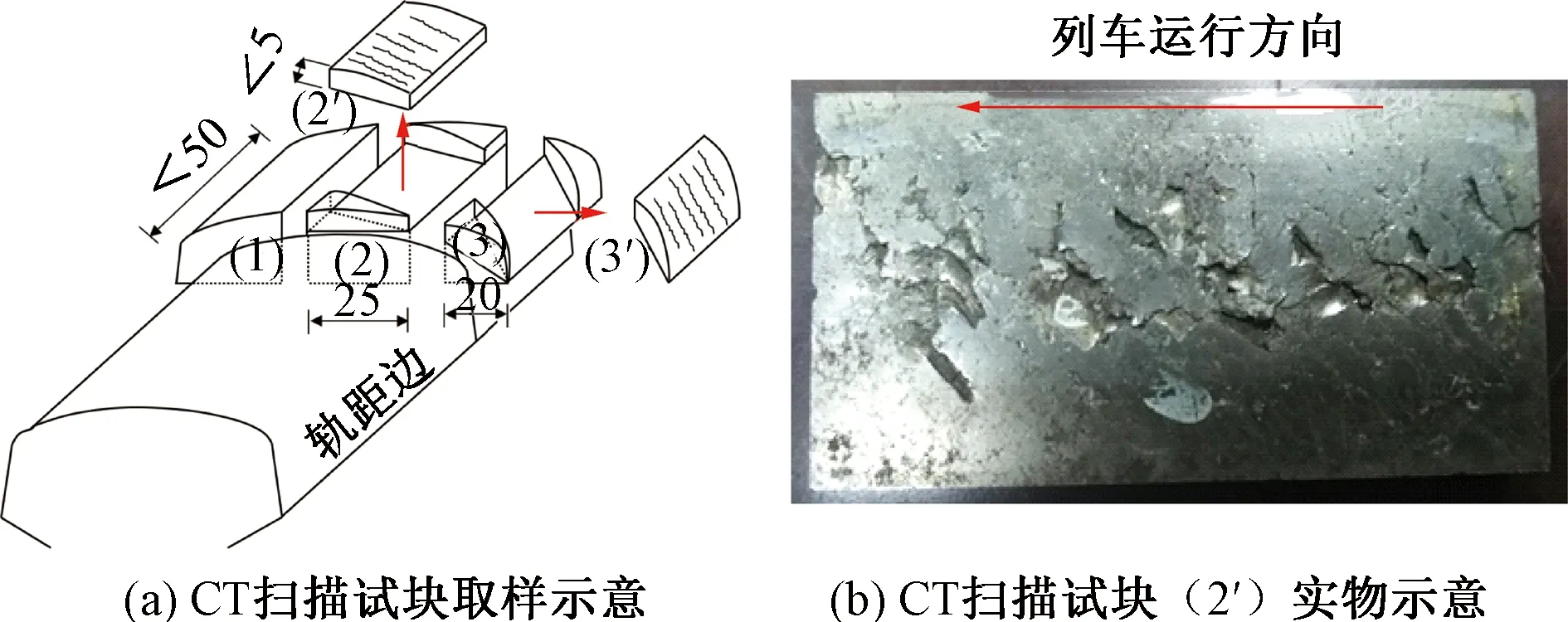
图5 含弯钩形裂纹试块取样示意

经过X射线断层扫描、灰度识别和描点，得到内轨取样试块表面的弯钩形裂纹，见图6。识别后裂纹由点云数据组成，每一个点都包含有三维空间坐标，相邻三个点组成微小的三角面片并带有面向量，所有面片再组合形成完整的裂纹形貌。

图6 弯钩形裂纹空间形态还原

由图6可以看出，扫描得到的弯钩形裂纹呈现明显的三维弯曲形态，在水平和垂直方向均呈曲线形态。

1.1.3 弯钩形裂纹三维数学模型

根据X射线断层扫描得到裂纹点云数据拟合裂纹尖端与开口。基于非均匀有理B样条理论(NURBS)[25-26]，首先定义1条p次的NURBS样条曲线为

(5)

式中：C(u)是曲线上任意点的三维空间坐标；Pi为控制点；Ni,p(u)为定义在节点矢量u上的p次B样条基函数；wi表权因子。

对于u向p次，v向q次的NURBS曲面，定义为

(6)

引入分段有理奇函数

(7)

则可将式(6)改写为

(8)

式中：S(u,v)为曲面上任意点的三维空间坐标，是关于曲面两个方向上参数u，v的函数；p、q为u，v方向曲面次数；wi,j为权因子；Pi,j为控制点，组成(n+1)×(m+1)的点阵网格；Ni,p(u)、Nj,q(v)分别为定义在节点矢量U、V上的非均匀有理B样条基函数：

(9)

其中，a、b分别为u节点矢量上的首尾两个节点；c、d分别为v节点矢量上的首尾两个节点；n、m分别为u、v所各包含的节点数量，且有r=n+p+1；s=m+q+1。

以裂纹尖端和开口所有凸点作为控制点拟合裂纹曲面见图7。

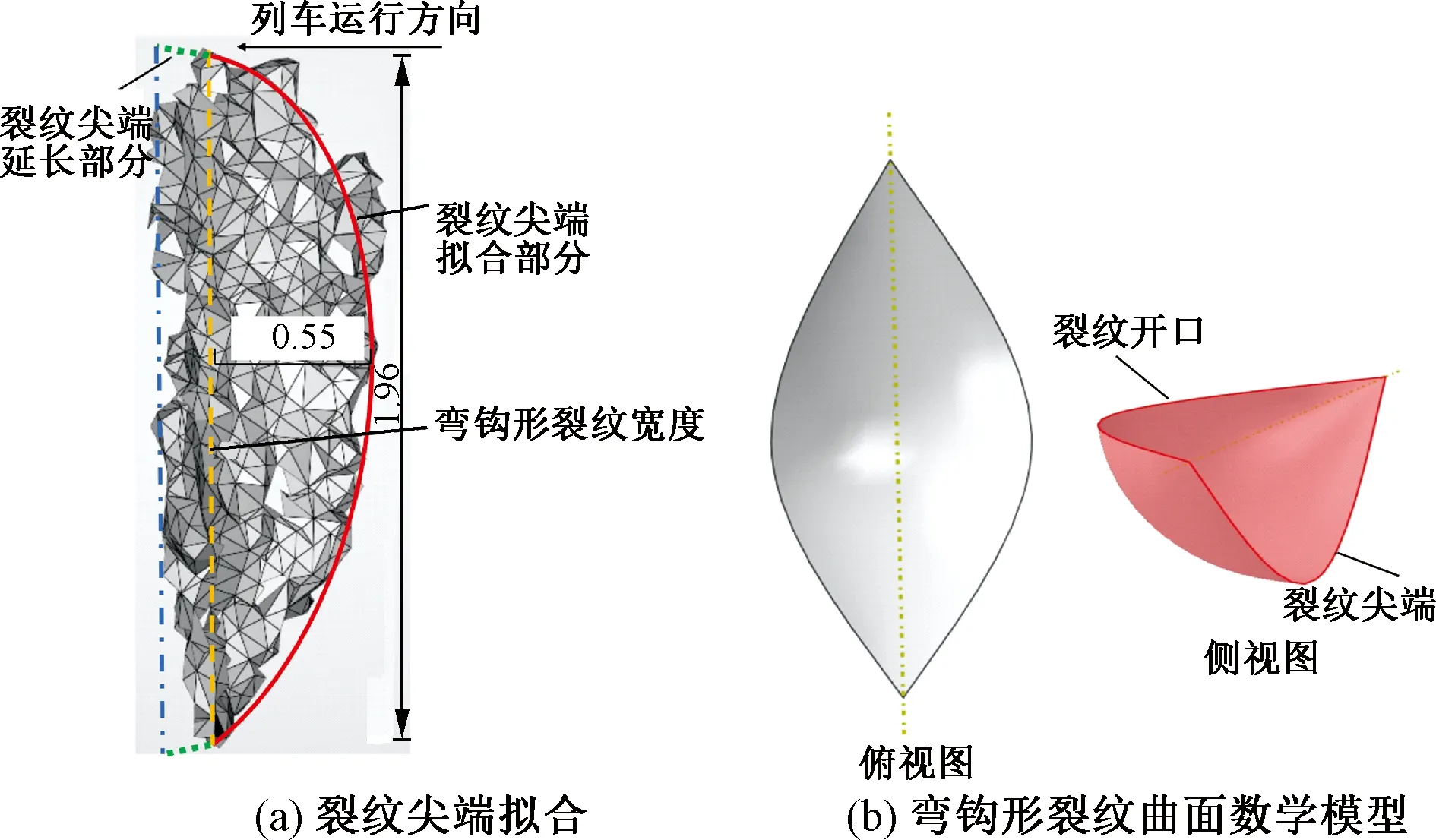
图7 基于NURBS的弯钩形裂纹曲面数学建模(单位：mm)

X射线断层扫描成像的弯钩形裂纹中部分空腔是由于扫描射线无法全部穿透该区域造成的，与该区域微观结构的致密程度和钢轨母材接近有关，其尺寸与整个裂纹相比较小，可以与周围结构融合[28]。图7(a)中红色实线和蓝色点划线是基于NURBS样条曲线拟合的裂纹尖端和开口有效部分；绿色短虚线条是基于裂纹尖端有效部分进行一定长度的延长；黄色虚线标示弯钩形裂纹宽度，是弯钩形裂纹深入到钢轨内部的最深位置为0.55 mm，拟合得到的裂纹曲面模型见图7(b)。

1.2 基于扩展有限元的弯钩形裂纹扩展预测模型

为反映裂纹扩展带来的非连续位移场，采用扩展有限元法[12]，在裂纹尖端附近单元引入富集函数[29]，其描述裂纹的近似位移插值矢量函数可表示为

(10)

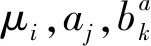
建立长为20 m的钢轨全局模型，其中扣件、轨枕、道床和基础简化成弹簧。截取全局模型中长度为200 mm的中段，作为含裂纹的钢轨局部子模型，其位移约束由车轮荷载作用在钢轨全局模型中得到[30]。通过显微观测和X射线断层扫描准确定位弯钩形裂纹在钢轨内部的空间位置，采用断裂力学分析软件FRANC3D将弯钩裂纹组装入钢轨子模型，用于计算裂纹扩展，裂纹尖端由六面体单元形成的三圈“单元环”组成，避免了计算时裂纹尖端处的奇异性问题，使裂纹面摆脱了必须沿单元边界扩展的桎梏，可在空间内任意方向扩展，钢轨局部子模型使用四面体单元，其与弯钩形裂纹尖端网格(三圈“单元环”)之间的联系采用金字塔形单元作为过渡，见图8。为描述裂纹尖端各点位置，将裂纹尖端的两端点分别定义为A点和B点，其中A点靠近轨距边，B点靠近轨顶中心。将裂纹尖端各点到A点的弧长与AB总弧长之比定义为各点的位置，这里主要关注除AB两端点之外的尖端各点应力强度因子和扩展情况，即各点位置为0.2～0.8，且裂纹尖端中点对应数值为0.5。

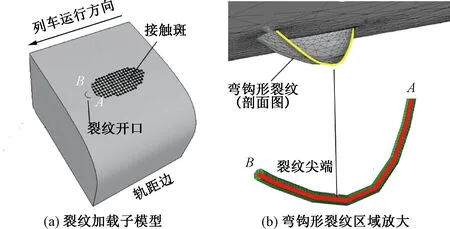
图8 弯钩形裂纹扩展预测模型

模型设置3种不同扩展阶段的裂纹，即裂纹深度不同：①完整裂纹：X射线断层扫描得到的完整弯钩形裂纹，深度为0.55 mm；②1/2裂纹：以完整弯钩形裂纹为基础，通过调整裂纹深度和空间旋转角度得到，其裂纹深度为完整弯钩形裂纹深度的1/2；③1/3裂纹，其裂纹深度为完整弯钩形裂纹深度的1/3。裂纹中心纵断面及与轮轨接触之间的关系见图9。

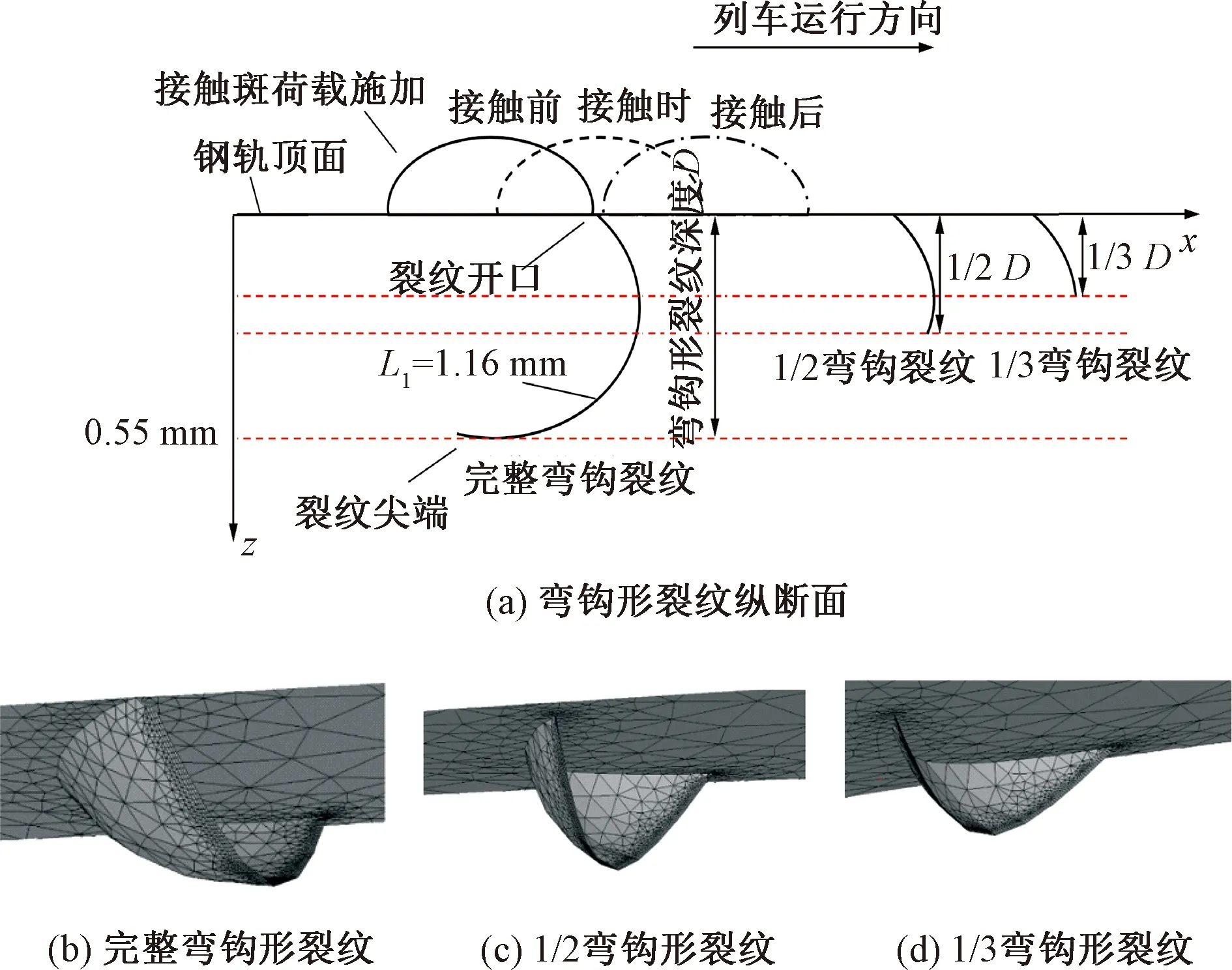
图9 三种扩展阶段的弯钩形裂纹

轮轨接触荷载由车辆-轨道多体动力学模型计算得到，包括接触斑尺寸、接触斑在钢轨上的位置、接触斑内黏着区-滑动区分布以及其上的法向应力和切向应力。沿列车运行方向，改变接触斑中心的坐标，使接触斑能够由裂纹开口的前端移动到末端[18]。本文接触荷载位置分别为：(1)接触斑前端位于裂纹开口处但尚未压上裂纹(定义为“接触前”)；(2)接触斑中心与裂纹开口中心重合(定义为“接触时”)；(3)接触斑后端在裂纹开口处(定义为“接触后”)。

1.3 疲劳断裂参量

1.3.1 应力强度因子

钢轨滚动接触疲劳裂纹属于复合型裂纹，轨顶面出现的弯钩形裂纹承受Ⅰ、Ⅱ、Ⅲ三种扩展类型共同作用[31]。采用M积分[32-33]计算三维裂纹尖端处所有节点的应力强度因子(KⅠ、KⅡ、KⅢ)，作为裂纹起裂扩展的评判标准为

M=∮Γ1(Wxini-Tkuk,ixi)dsi,k=1,2

(11)

式中：M为裂纹尖端扩展的能量释放率；Γ1为任意一条围绕裂纹尖端的积分路径；W为应变能密度因子；Tk=σjknk为积分路径外法线方向主应力矢量；ni为积分路径Γ1的外法线方向矢量，下标i表示对xi的偏导数。

基于M积分的应力强度因子分别为

(12)

(13)

(14)

式中：r为裂纹尖端任意点o′至微元P的空间距离；θ为直线o′P投影至xoy平面后与x轴夹角；z为微元P的空间竖坐标。

1.3.2 弯钩形裂纹扩展速率

利用最小应变能密度因子理论[34-35]计算等效应力强度因子Kequiv为

(15)

式中：γⅡ、γⅢ分别为Ⅱ、Ⅲ型裂纹应力强度因子在等效应力强度因子Kequiv中的权重系数。

进而修正Paris公式为[36]

(16)

式中：a为裂纹深度；c为与材料有关的参数。

1.3.3 磨耗对裂纹扩展影响

钢轨垂直磨耗会减小包括裂纹在内的钢轨表层材料，根据修正后的Paris公式(16)，考虑垂直磨耗在弯钩形裂纹整个扩展寿命阶段对裂纹扩展速率的影响，垂直磨耗平均发展率Vwear的计算公式为[37]

(17)

式中：Hv为通过总重累积阶段内垂直磨耗深度；N为通过总重累积阶段内车轮通过次数。

考虑垂直磨耗影响后弯钩形裂纹的净裂纹扩展速率计算式为

(18)

式中：da/dN为弯钩形裂纹的净扩展速率；Vwear为垂直磨耗平均发展率；θ为弯钩形裂纹和钢轨表面的夹角。

2 弯钩形裂纹扩展预测

2.1 裂纹尖端应力强度因子变化

轮轨接触荷载作用在裂纹开口之前时，不同深度裂纹尖端应力强度因子分布见图10。

由图10可知，从裂纹尖端应力强度因子为正来判断，接触前裂纹的扩展形式以Ⅰ、Ⅲ型开裂扩展为主。

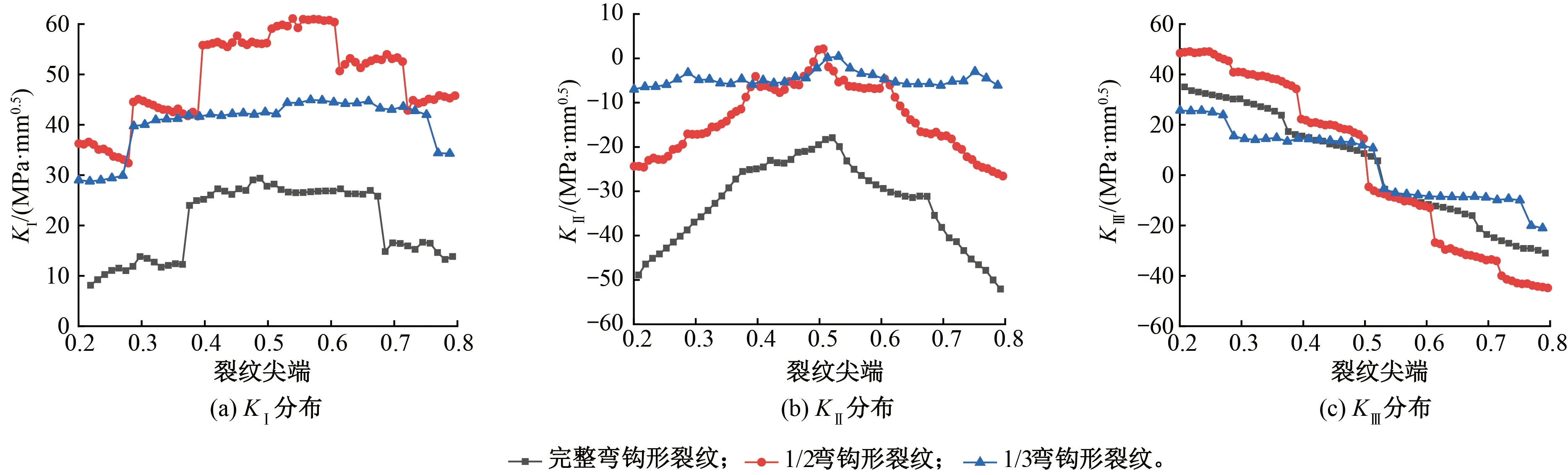
图10 接触前弯钩形裂纹尖端KⅠ、KⅡ和KⅢ分布

(1)张开效应(Ⅰ型开裂)：KⅠ沿裂纹尖端呈现中间凸、两边低的分布，即裂纹中部及其附近受荷载影响明显；1/3和1/2裂纹的I型应力强度因子大于完整裂纹的，说明裂纹在没有达到路径变化时有较强的I型开裂扩展趋势。

(2)滑开效应(Ⅱ型开裂)：尽管分布特征与KⅠ相似，但KⅡ沿裂纹尖端均为负，滑开效应处于被抑制阶段。

(3)撕开效应(Ⅲ型开裂)：从近轨距角(横坐标0.2)至近轨顶中心(横坐标0.8)，KⅢ呈由正到负的降低趋势，主要在裂纹尖端中心附近发生正负号变化。由此，在裂纹尖端0.2～0.5区间，即靠近轨距边一侧，裂纹扩展的撕开效应随裂纹深度增加呈先增后降趋势，从1/3裂纹到1/2裂纹时，裂纹的撕开效应逐渐增大，从1/2裂纹到完整裂纹，裂纹的撕开效应逐渐减小；裂纹尖端0.5～0.8区间，接触前不同深度弯钩形裂纹Ⅲ型应力强度因子为负，不具有撕开效应。

轮轨接触荷载作用在裂纹开口时，不同深度裂纹尖端应力强度因子分布见图11。由图11可知，接触时裂纹的扩展形式以Ⅱ、Ⅲ型开裂扩展为主。

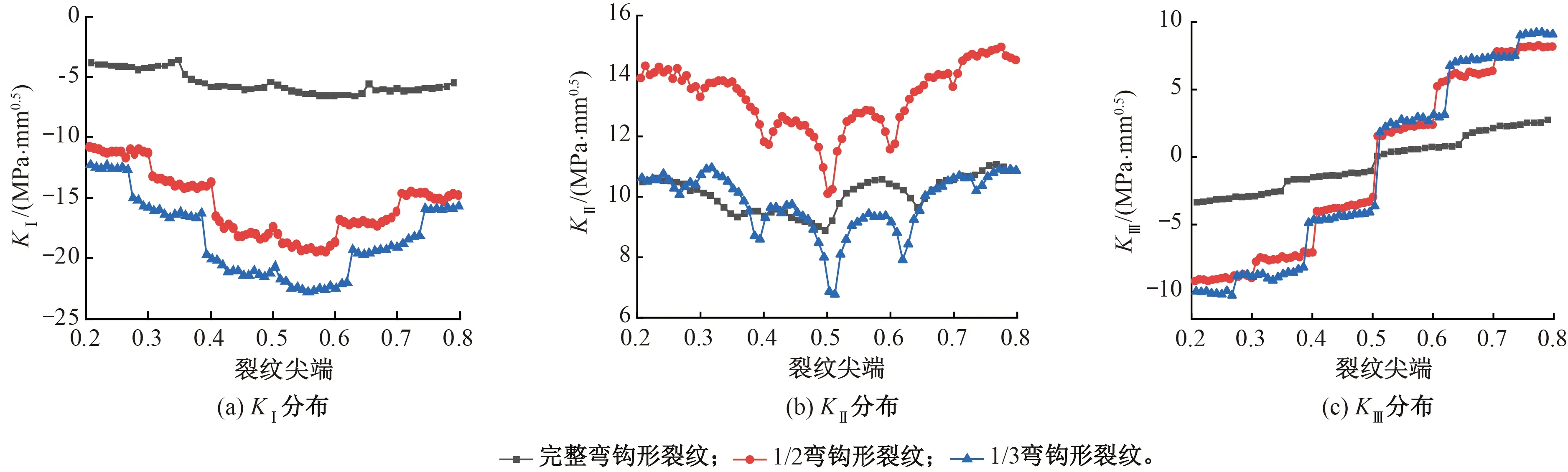
图11 接触时弯钩形裂纹尖端KⅠ、KⅡ、KⅢ分布

(1)张开效应：KⅠ沿裂纹尖端均为负，张开效应处于抑制阶段。从1/3裂纹到完整深度裂纹时，抑制作用逐渐减弱。

(2)滑开效应：KⅡ沿裂纹尖端呈现中间凹、两边高的分布，即裂纹两端及其附近滑开效应明显；不同裂纹深度下，1/3裂纹和完整裂纹时的尖端强度因子小于1/2深度的，说明裂纹在发展初期和末期时的滑开效应较小，Ⅱ型开裂扩展在裂纹发展过程中呈现先增后降趋势。

(3)撕开效应：裂纹尖端0.2～0.8区间段，KⅢ呈由负到正的增长趋势，在裂纹尖端中心附近发生正负号转变；裂纹尖端0.2～0.5区间，即靠近轨距边一侧，接触时Ⅲ型应力强度因子为负，不具有撕开效应；裂纹尖端0.5～0.8区间，即靠近轨顶中心一侧，裂纹扩展的撕开效应随裂纹深度增加呈降低趋势，从1/3裂纹到完整裂纹，裂纹的撕开效应逐渐减小。

轮轨接触荷载作用在裂纹开口后，不同深度裂纹尖端应力强度因子分布见图12。由图12可知，接触后裂纹的扩展形式以Ⅱ、Ⅲ型开裂扩展为主。

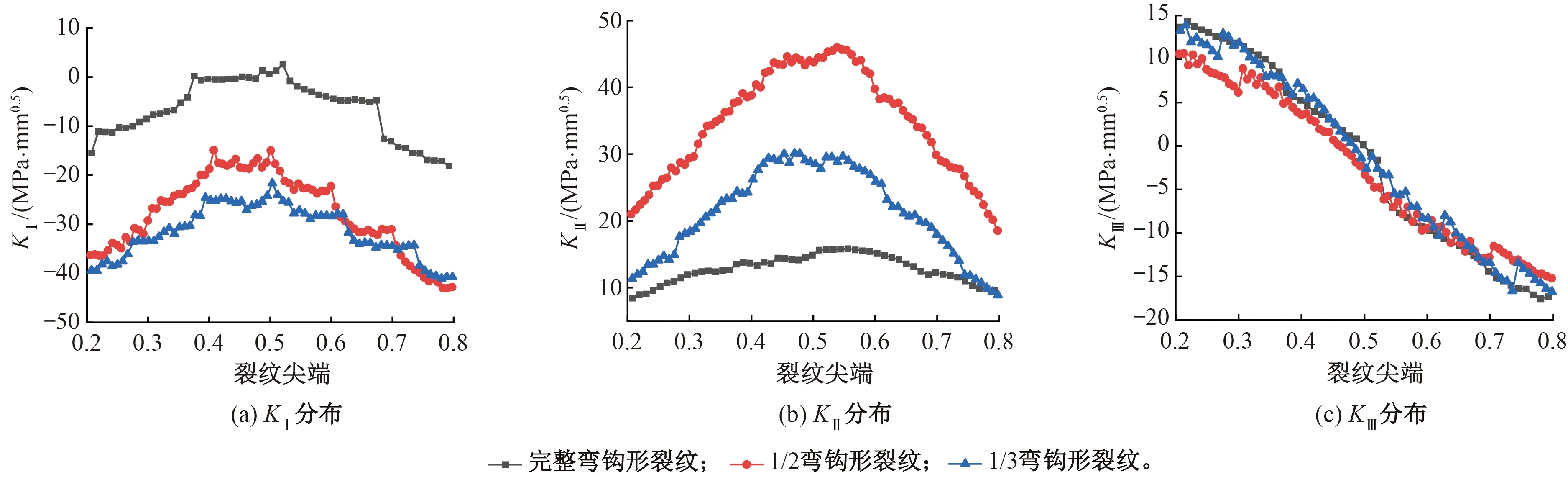
图12 接触后弯钩形裂纹尖端KⅠ、KⅡ和KⅢ分布

(1)张开效应：接触后KⅠ沿裂纹尖端均为负，张开效应处于抑制阶段。

(2)滑开效应：KⅡ沿裂纹尖端呈现中间凸、两边低的分布，裂纹尖端中部及其附近受荷载影响明显；完整裂纹的尖端Ⅱ型应力强度因子最小，1/2裂纹的Ⅱ型应力强度因子大于1/3裂纹的，Ⅱ型开裂扩展在裂纹发展过程中呈现先增后降趋势。

(3)撕开效应：裂纹尖端0.2～0.8区间段，KⅢ呈由正到负的降低趋势，主要在裂纹尖端中心附近发生正负号变化；裂纹尖端0.2～0.5区间(靠近轨距边一侧)具有撕开效应，且越靠近轨距边一侧，撕开效应越大；裂纹尖端0.5～0.8区间，接触后不同深度弯钩形裂纹Ⅲ型应力强度因子为负，不具有撕开效应。

综上所述，在轮轨接触荷载逐渐通过裂纹开口时，裂纹扩展受呈现张开、滑开和撕开效应的复合开裂，在轮轨接触前，裂纹全部尖端受到张开效应作用，靠近轨距边一侧的裂纹尖端还受到撕开效应作用；在接触时，裂纹全部尖端受到滑开效应作用，靠近轨顶中心一侧的裂纹尖端受到撕开效应作用；接触后，裂纹全部尖端受到滑开效应作用，靠近轨距边一侧的裂纹尖端还受到撕开效应作用。1/3裂纹和1/2裂纹的尖端应力强度因子比完整裂纹的要高，说明在较浅的裂纹有扩展的趋势，而扩展到一定深度、发生路径变化后的完整裂纹，扩展趋势有所降低。

2.2 完整弯钩形裂纹扩展速率预测

以三维重构的完整弯钩形裂纹为初始裂纹，以接触前、接触时和接触后三个荷载依次经过裂纹开口作为一次车轮循环，cycle。考虑磨耗影响，通过现场观测内轨在通过总重为100～150 MGT时的型面变化，基于式(17)计算得到钢轨平均磨耗发展率为Vwear为0.104 nm/cycle，预测通过总重达到150 MGT时弯钩形裂纹的扩展速率及扩展角度，见图13。

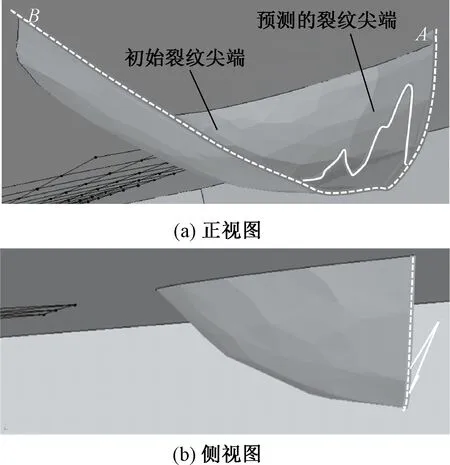
图13 通过总重为150 MGT时弯钩形裂纹扩展预测结果

在图13中，沿裂纹尖端的白色点线为通过总重100 MGT时的弯钩形裂纹尖端，即初始裂纹尖端，白色实线为通过总重达到150 MGT时新的裂纹尖端，即预测的裂纹尖端。由图13可以看出，随着通过总重的增加，裂纹尖端各个节点处的扩展速率并不相同，与真实裂纹尖端形状下尖端各点应力强度因子的分布不均有关，A点一侧(裂纹尖端近轨距边一侧)到裂纹尖端中部位置的扩展速率较大，并在裂纹尖端中部位置附近取得最大值，裂纹尖端靠近A点和B点的两个端部附近裂纹扩展速率较小，因为，此处三类应力强度因子均取得最小值，并且端部受磨耗影响最大，最先被磨损掉。

为方便描述并与显微观测对比，截取裂纹尖端中部位置即裂纹尖端扩展速率最大处进行对比，见表1，其中，裂纹扩展速率由式(17)计算得到。

表1 通过总重为150 MGT时弯钩形裂纹扩展预测结果

2.3 裂纹扩展预测对比验证

将表1预测结果与现场150 MGT时的显微观测结果进行对比。由于初始裂纹和对比裂纹来源于不同通过总重时的钢轨取样，这些裂纹处于同一线路条件但不是同一裂纹。因此，统计通过总重150 MGT所有取样钢轨观测裂纹的长度和角度范围，显微观测裂纹扩展长度为观测长度减去2.1节X射线断层扫描提取的通过总重为100 MGT时弯钩形裂纹的长度Ll(1.23 mm)，结果见图14和表2。

图14 通过总重为150 MGT时内轨弯钩形裂纹纵断面显微观测

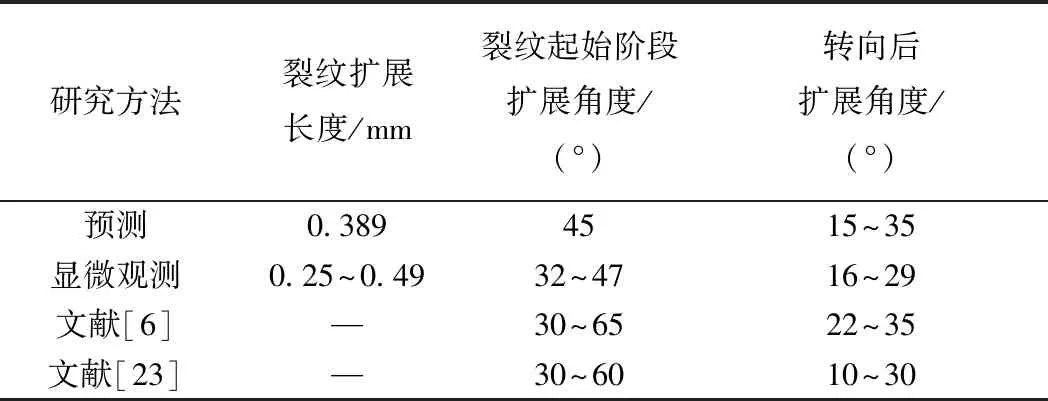
表2 裂纹扩展预测结果对比验证

由表2可知，预测的弯钩形裂纹扩展角度包含了显微观测的角度范围，且与文献[4]和文献[21]中关于弯钩形裂纹在转向前后的扩展角度基本一致。同时，从图13和图14对比来看，弯钩形裂纹后续扩展呈现向轨顶面扩展的趋势，预测结果和现场情况吻合。

3 结论

本文基于X射线断层扫描技术，测量了弯钩形裂纹的三维形貌，建立了基于三维重构的弯钩形裂纹扩展预测模型，得到以下结论。

(1)弯钩形裂纹的扩展是张开、滑开和撕开效应结合的复合开裂。在轮轨接触前，裂纹全部尖端受到张开效应作用，靠近轨距边一侧裂纹尖端还受到撕开效应作用；在接触时，裂纹全部尖端受到滑开效应作用，靠近轨顶中心一侧裂纹尖端受到撕开效应作用；接触后，裂纹全部尖端受到滑开效应作用，靠近轨距边一侧裂纹尖端还受到撕开效应作用。

(2)深度较浅、尚未发生路径转向的1/3、1/2深度裂纹尖端应力强度因子大于完整裂纹，说明荷载作用下、裂纹发展初期浅裂纹的扩展明显；当裂纹扩展到一定深度，发生路径转变后，裂纹的扩展逐渐减小。

(3)裂纹在空间内不同尖端位置的应力强度因子不同。裂纹尖端中部的应力强度因子较大，其扩展速率最快；尖端中部两侧应力强度因子较小，受张开效应、滑开效应和撕开效应抑制作用明显，裂纹扩展速率明显小于尖端中部，裂纹在空间内以一定角度呈“凸”字形不均匀发展。

(4)以通过总重100 MGT的弯钩形裂纹为初始值，考虑磨耗影响，预测当弯钩形裂纹在通过总重达到150 MGT时，裂纹尖端中部的裂纹扩展速率为0.178 nm/cycle，裂纹扩展长度为0.389 mm，转向后弯钩形裂纹扩展角度为15°～35°。预测的裂纹长度与现场观测值较接近，显微观测的实际扩展角度在预测扩展角度范围内。

本文预测方法仍属于静态分析，后续拟采用近场动力学、相场理论等建立弯钩形裂纹动态扩展模型并研究其路径动态变化规律和剥离掉块成因。