钢-混凝土混合梁三塔斜拉桥结构参数敏感性分析

过黄喜

(长沙理工大学 土木工程学院，湖南 长沙 410114)

斜拉桥是由塔、梁、索组成的高次超静定结构体系，受施工过程中施工误差和环境因素的影响，成桥后线形和内力状态与设计理论状态会存在一定偏差。主梁质量、温度和材料参数等变化都会影响施工控制，造成成桥后结构响应与设计状态有所偏差。目前对独塔和双塔斜拉桥的参数分析较多，如张宪堂等对双塔双索钢箱梁斜拉桥的参数敏感性进行研究，确定了监控关键控制量，为结构参数识别及误差修正提供了科学依据；邬晓光等对双钢拱塔斜拉桥进行参数敏感性分析，结果显示整体温度作用及拉索初张力对双钢拱塔斜拉桥成桥状态钢主梁竖向位移、钢主梁截面上下缘应力、塔顶变形、塔底截面应力、拉索索力影响较大,为敏感参数，结构容重、拉索弹性模量为非敏感参数。但对三塔钢-混凝土混合梁斜拉桥的参数分析较少。该文针对泸州某钢-混凝土混合梁斜拉桥的结构特点，通过MIDAS/Civil有限元软件建立模型，对该桥施工过程中的设计参数进行敏感性分析，研究主梁线形、主梁应力、斜拉索索力的变化规律，确定结构的敏感参数及其影响范围。

1 工程背景

某三塔双索面斜拉桥的跨径布置为(55+60+425+425+60+55) m，其中2个主跨各有391 m钢箱梁，其余均为混凝土箱梁(见图1)。根据锚箱位置不同，分别采用分离式双箱和单箱多室的截面形式，主梁中心线处主梁内轮廓高3.97 m，主梁全宽49.0 m，斜底板宽11.892 6 m，水平底板宽分别为10.208 m(分离双箱)、27.175 6 m(单箱)。钢箱梁顶面设2%双向横坡，底面水平(见图2)。

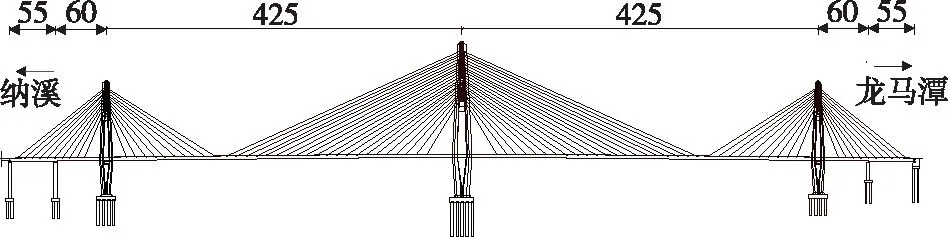
图1 桥梁结构布置(单位：m)

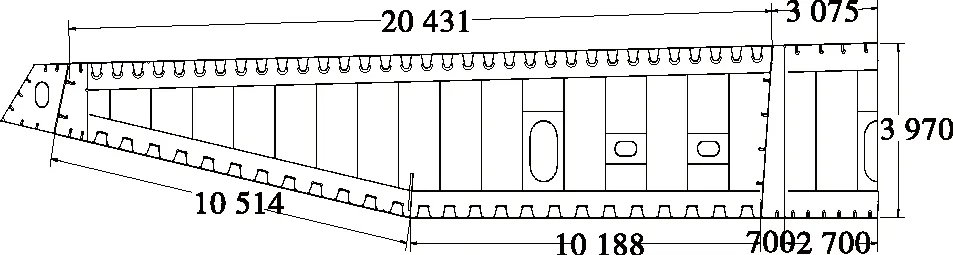
图2 钢箱梁主梁断面示意图(单位：mm)

主塔采用高低塔结构，高低桥塔均设置于桥面中分带，横桥向为独柱形式，纵桥向为分肢菱形造型。高塔斜拉索呈空间索面扇形布置，低塔斜拉索呈平行索面扇形布置。高塔斜拉索在梁上锚固于箱梁外侧边腹板与横隔梁相交的边缘位置，单侧共21对斜拉索，索梁锚固点顺桥向标准间距为12.0 m，从最短索开始的6对拉索的索塔锚固点竖向间距为2.0 m，上面4对拉索的索塔锚固点竖向间距为3.0 m。低塔斜拉索在梁上锚固于箱梁中部小纵梁，单侧共10对斜拉索，钢梁段索梁锚固点顺桥向标准间距为12.0 m，混凝土梁段索梁锚固点顺桥向标准间距为9.0 m。

2 计算模型及结构参数

2.1 结构模型

应用MIDAS/Civil软件建立全桥有限元模型(见图3)，对全桥进行施工过程模拟分析和控制计算。模型共1 066 个节点、776个单元，其中桁架单元168个。主梁和主塔均采用梁单元模拟，斜拉索采用桁架单元模拟。斜拉索与主梁、主塔之间均采用刚性连接，辅助墩墩底和主塔塔底施以竖向、横向、纵向约束，在中塔和边塔位置对主梁同样施加竖向、横向、纵向约束。

图3 桥梁结构有限元模型

2.2 结构参数

桥梁主跨采取悬臂拼装法施工，在主梁合龙前主梁处于悬臂状态，随着悬臂施工长度的增加，主梁柔度增加，合龙后结构体系发生转变，主梁合龙前后的结构刚度相差悬殊，较小的结构参数误差都将引起较大的梁段标高、主梁应力误差。结合工程实际情况及相关文献资料，选取主梁自重、斜拉索索力及弹性模量等作为结构分析参数，分析时仅改变单一参数，分别计算桥梁成桥状态下主梁线形、主梁应力、斜拉索索力，分析结构参数对桥梁结构的影响。

3 计算结果分析

3.1 主梁自重影响分析

鉴于钢箱梁厂家制造和现场施工、拼装误差，难以避免出现梁段重量超重或超轻的情况。在钢箱梁和混凝土梁自重参数设计值的基础上同时变化±2%、±5%，其他参数不变，计算成桥后主梁线形、主梁应力及斜拉索索力，结果见表1、图4。

由图4、表1可知：主梁自重变化对结构成桥状态的影响较大，自重变化±2%、±5%，主线线形的整体波动趋势基本一致，最大变化幅度随自重变化的增大而增大，主要变化集中在主跨，边跨混凝土梁的结构响应变化比主跨钢箱梁的结构响应变化小。主梁自重变化±2%时，主跨线形最大变化值为22.1 mm、变化幅度为1.3%，主梁应力最大变化值为4.0 MPa、变化幅度为9.0%，索力最大变化值为70.7 kN、变化幅度为0.8%；边跨线形最大变化值为1.1 mm、变化幅度为4.4%，最大应力变化值为0.1 MPa、变化幅度为2.2%，最大索力变化值为43.8 kN、变化幅度为0.1%。主梁自重变化±5%时，主跨线形最大变化值为54.9 mm、变化幅度为3.2%，应力最大变化值为10.0 MPa、变化幅度为3.6%，索力最大变化值为176.6 kN、变化幅度为2.0%；边跨线形最大变化值为2.8 mm、变化幅度为11.7%，最大应力变化值为0.5 MPa、变化幅度为3.6%，最大索力变化值为120.4 kN、变化幅度为2.0%。

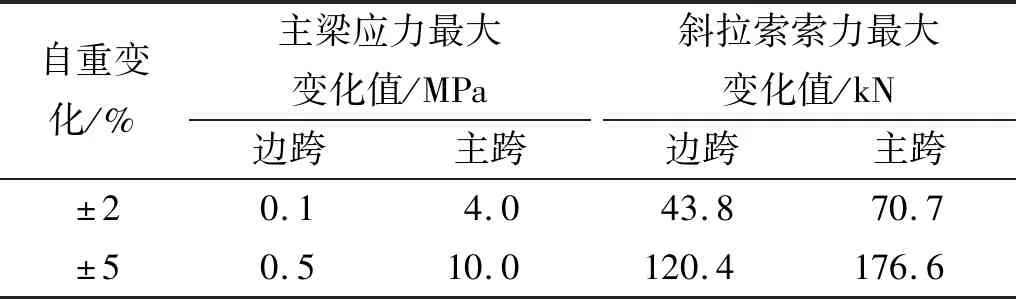
表1 自重变化时主梁应力和斜拉索索力的变化

图4 自重变化对主梁线形的影响

3.2 斜拉索张拉索力影响分析

该桥采用悬臂拼装法施工，考虑温度作用、风荷载及施工误差的影响，悬臂拼装过程中MP4中塔两侧的斜拉索顺桥向和横桥向都会出现索力偏差。在中塔斜拉索顺桥向和横桥向张拉索力设计值的基础上变化±3%、±5%、±10%，其他参数不变，计算成桥状态下主梁线形、主梁应力及斜拉索索力。

中塔顺桥向龙马潭侧斜拉索索力变化时主梁线形、主梁应力及斜拉索索力的变化见图5和表2。由图5、表2可知：斜拉索索力变化对主梁线形的影响很大，影响主要集中在张拉索力改变的龙马潭侧主跨，张拉索力改变越大，变化幅度越大；对纳溪侧主跨及边跨的影响极小。张拉索力变化±3%时，主梁线形最大变化值为48.1 mm、变化幅度为2.8%，主梁应力最大变化值为8.0 MPa、变化幅度为3.1%，成桥索力最大变化值为128.2 kN、变化幅度为2.5%；张拉索力变化±5%时，主梁线形最大变化值为80.3 mm、变化幅度为4.6%，主梁应力最大变化值为13.0 MPa、变化幅度为4.7%，成桥索力最大变化值为213.9 kN、变化幅度为4.2%；张拉索力变化±10%时，主梁线形最大变化值为161.7 mm、变化幅度为9.3%，主梁应力最大变化值为25.0 MPa、变化幅度为9.8%，成桥索力最大变化值为428.7 kN、变化幅度为8.5%。

图5 顺桥向索力变化对主梁线形的影响

表2 顺桥向索力变化时主梁应力和斜拉索索力的变化

中塔横桥向上游侧斜拉索索力变化时主梁线形、主梁应力及斜拉索索力的变化见图6和表3。由图6、表3可知：张拉索力变化对主梁线形、主梁应力和成桥索力的影响很大，主要变化集中在中塔两侧主跨，张拉索力变化越大，变化幅度越大。张拉索力变化±3%时，主梁线形最大变化值为23.9 mm、变化幅度为1.4%，主梁应力最大变化值为4.0 MPa、变化幅度为2.0%，成桥索力最大变化值为127.1 kN、变化幅度为2.5%；张拉索力变化±5%时，主梁线形最大变化值为39.9 mm、变化幅度为2.3%，主梁应力最大变化值为7.0 MPa、变化幅度为2.8%，成桥索力最大变化值为212.0 kN、变化幅度为4.2%；张拉索力变化±10%时，主梁线形最大变化值为80.2 mm、变化幅度为4.6%，主梁应力最大变化值为14.0 MPa、变化幅度为5.1%，成桥索力最大变化值为425.1 kN、变化幅度为8.4%。

表3 横桥向索力变化时主梁应力和斜拉索索力的变化

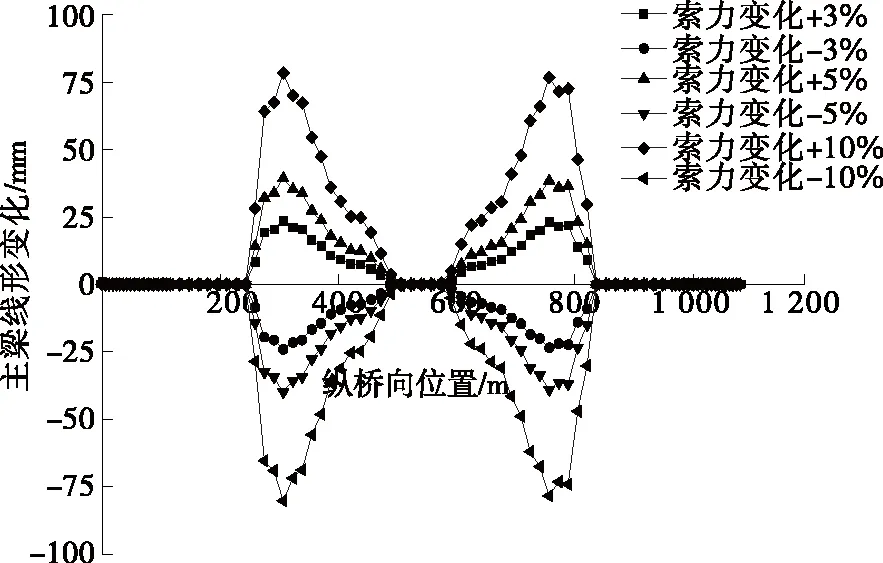
图6 横桥向索力变化对主梁线形的影响

3.3 斜拉索弹性模量影响分析

钢丝的弹性模量和面积是斜拉索主要刚度误差来源，一般情况下，钢丝制作精度高，高强钢丝的弹性模量较稳定，则面积和弹性模量的误差较小。由于斜拉桥跨径较大，索的垂度效应会引起索的轴向刚度下降，通常通过换算弹性模量来修正。在斜拉索弹性模量设计值1.95 MPa的基础上变化±2%、±5%，其他参数不变，计算成桥状态下主梁线形、主梁应力及斜拉索索力，结果见图7和表4。

图7 斜拉索弹性模量变化对主梁线形的影响

表4 斜拉索弹性模量变化时主梁应力和斜拉索索力的变化

由图7、表4可知：斜拉索弹性模量对主梁线形、主梁应力、斜拉索索力有一定影响，主要变化集中在中塔两侧主跨，变化幅度随着斜拉索弹性模量的增大而增大。弹性模量变化±2%时，主梁线形最大变化值为27.8 mm、变化幅度为1.6%，主梁应力最大变化值为2.0 MPa、变化幅度为1.2%，成桥索力最大变化值为14.9 kN、变化幅度为0.2%；弹性模量变化±5%时，主梁线形最大变化值为71.5 mm、变化幅度为4.2%，主梁应力最大变化值为6.0 MPa、变化幅度为2.1%，成桥索力最大变化值为37.9 kN、变化幅度为0.5%。

4 结论

(1) 桥梁整体主梁自重对结构影响显著，属于敏感参数。主梁自重变化引起的边跨混凝土梁的结构响应远小于主跨钢箱梁的结构响应，斜拉桥施工过程中需严格把控主跨钢箱梁节段重量。

(2) 斜拉索张拉索力对桥梁结构的影响很大，中塔空间索横向、纵向索力的改变对成桥响应都有重要影响，纵桥向索力改变造成的结构响应大于横桥向索力改变造成的结构响应。为保证结构安全，斜拉桥施工过程中需控制斜拉索张拉力，确保索力精准。

(3) 对于主梁成桥线形，敏感因素影响程度排序依次为斜拉索张拉索力、主梁自量、拉索弹性模量；对于成桥主梁应力，敏感因素影响程度排序依次为斜拉索张拉索力、斜拉索弹性模量、主梁梁段重量；对于成桥索力，敏感因素影响程度排序依次为斜拉索张拉索力、钢箱梁梁段重量、斜拉索弹性模量。