例谈伸缩变换法在解题中的应用

江苏省如皋中学 (226500) 王宏兵

1.伸缩变换的定义

2.伸缩变换的性质

本文先给出几条伸缩变换的常用性质，再利用这些性质破解几道椭圆的最值问题和中点弦问题.

(1)经过上述伸缩变换φ，点M变换为点M′，直线l变化为直线l′，若点M∈直线l，则点M′∈直线l′；

(2)经过伸缩变换φ，对应地l→l′,m→m′，若直线l∥直线m，则变换后l′∥m′，若直线l∩直线m=点P，则变换后直线l′∩直线m′=点P′；

3.伸缩变换的应用

评注：借助伸缩变换将椭圆化为圆，将问题转化成计算圆上的到与它相离的直线的距离最小时的点的坐标，减少了运算量.

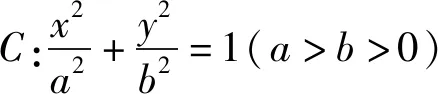
(1)求C的方程；

(2)点N为C上一动点，求△AMN的面积的最大值.

评注：本题第(2)问运用伸缩变换法将求椭圆的给定条件的内角三角形面积问题化归为单位圆的内接三角形面积问题，运用点到直线距离公式、圆的弦长公式以及圆的几何性质可以顺利解答，降低了运算量.

评注：本题是一道椭圆的定值问题，如果运用直角坐标法的话运算量非常大，本解法运用伸缩变换法将椭圆中的问题化归为圆中的问题，由等边三角形的性质：若一个三角形的外心与内心重合，则这个三角形为等边三角形，可以确定△A′B′C′为等边三角形，再运用正弦定理可以计算出其面积，由伸缩变换的性质，可以确定△ABC的面积为定值.

圆和椭圆的都是高中数学主干知识，运用伸缩变换法体现的是化归与转化思想的运用，将椭圆中的问题化归为圆中的问题，相比较可以简化数学运算和沟通数学知识之间联系，落实数学运算、逻辑推理和直观想象数学核心素养的培养，促进学生深度学习，培养学生创新思维.由于伸缩变化法解答双曲线和抛物线问题不那么简洁完美，本文不再探讨.伸缩变换法在椭圆问题中更广泛的应用有待于在教学和学习实践中进一步探究和总结.