一道三角形面积最小值问题的多解探究
2022-08-09黑龙江省大庆第一中学163000
黑龙江省大庆第一中学 (163000) 程 欣
解三角形是高考数学常考知识点,若涉及求解三角形面积的最小值,则往往需要考虑基本不等式或三角函数知识在解题的灵活、综合运用,求解此类问题有利于帮助我们顺利破解目标,提高分析解决问题的能力.
1.题目呈现
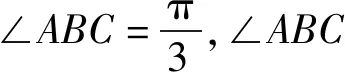
2.解法探究

思路1:(面积法)处理解三角形问题时,根据具体的图形,可考虑利用“分割组合思想”,有利于从面积角度出发去分析、运用图形特征,进而为目标问题的获解创造有利条件.

评注:该解法的关键是先得到边长a,c满足的关系式,再灵活运用基本不等式加以求解.
思路2:(建系法)由于解三角形问题涉及到具体的平面图形,所以可在适当建立平面直角坐标系的基础上,灵活运用有关解析几何知识,或者有关平面向量知识加以求解.


图1


思路3:(向量法)由于平面向量具有“数”和“形”的双重功能,所以处理有关解三角形问题时,可结合图形,考虑有关平面向量知识(尤其是向量的线性表示)在解题中的灵活运用.


思路4:(定理法)处理解三角形问题,最基本最常用的方法就是考虑正、余弦定理的灵活运用.需要关注两点:一是余弦定理的“多次”运用;二是先巧作辅助线,再灵活运用正、余弦定理解题.
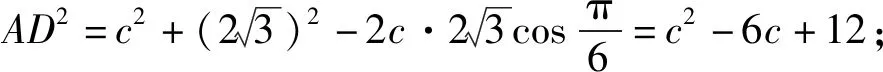


图2
评注:解法4体现了三角形角平分线性质定理与余弦定理的综合运用;而解法5体现了线线平行的性质与正弦定理的综合运用.此外,还可以过点D作BC的平行线,进行求解.
思路5:(平几法)由于解三角形问题,涉及具体的平面图形,所以可在适当巧作辅助线的基础上,有意识地去考虑初中所学平面几何知识在解题中的灵活运用.


图3
评注:该解法完全是根据初中平面几何知识,求得2(a+c)=ac,故值得关注、学习!
思路六:(参数法)处理三角形面积最值问题时,可结合图形,灵活引入角参数,将三角形的面积表示成关于角参数的函数表达式,从而可借助有关三角函数知识加以灵活求解.

评注:该解法的关键是引入角参数,将目标问题等价转化为求三角函数表达式的最小值.
3.推广探究

4.解后反思
综上,本题设计较好,看似简单,实则内涵丰富,具有较强的训练价值和研究价值.显然,不同的思维切入点,往往可以获得不同的解题体验,真可谓“横看成岭侧成峰,远近高低各不同”,需要我们在学中“悟”,在“悟”中不断提升解题的技能技巧.
从本质上讲,借助“一题多解”的教研方式,不仅有利于帮助我们突破以往的局限性解题思维模式,探寻最优解题思维;而且也有利于帮助我们逐步实现举一反三、融会贯通之目的.因此,在未来的数学学习中,我们可以选取一些典型试题,深层次挖掘,拓宽解题思维,促进教师的专业成长,进一步提升数学核心素养.
