复杂环境下BDS+GPS系统RTK短基线定位算法研究
2022-08-09刘海波郭志强吴绩伟
刘海波,杨 杰,张 旭,郭志强,吴绩伟,凌 强
(1.武汉理工大学信息工程学院,湖北 武汉 430070;2.上海国际港务(集团)股份有限公司,上海 200000)
实时动态(real-time kinematic,RTK)定位和精密单点定位(precise point positioning,PPP)是卫星定位的两个主要发展方向。对于有限区域范围内的实时高精度定位,如公司、大型港口等地区的车辆货物定位需求,采用RTK可以获得更高的位置精度和实时响应能力。该定位方式可以获得厘米级精度,但是实际使用效果受限于基线长度、可用卫星信号数量、整周模糊度解算效率和多径效应等因素[1]。
中国着眼于国家安全和社会发展需要,从1970年开始研究卫星导航系统相关技术,先后建立北斗一号系统、北斗二号系统、北斗三号系统,于2020年7月宣布北斗三号卫星导航系统正式面向全球提供全天候的定位、导航和授时服务。充分利用具有独特优势的北斗导航系统(beidou navigation satellite system,BDS),可以提高RTK在复杂环境下的定位精度。
近几年,国内外学者在北斗系统信号质量以及北斗系统RTK定位方面做了大量研究工作[2-12],文献[2]研究了不同卫星高度截止角对卫星定位精度的影响;文献[3]分析了北斗地球静止轨道卫星和倾斜轨道卫星的信号质量,评估了北斗双频信号在短基线下的定位精度;文献[4]提出了一种基于卡尔曼滤波的算法来估计BDS和GPS短基线解算时的整周模糊度;文献[5]利用迭代法来提高伪距单点定位精度;文献[6]对比了BDS+GPS单频双系统和双频单系统的定位性能,结果表明单频双系统可以在高卫星截止角的情况下提供更好的整周模糊度解算性能和位置精度;文献[7]提出了一种单双频GPS+BDS双系统融合的混合双差分RTK处理算法;文献[8]研究了导航系统的系统间偏差,在RTK经典差分法的基础上提出了一种新的差分方法;文献[9]对比分析了城市环境下BDS、GPS、BDS+GPS三种模式下的单频RTK定位性能和解算精度;文献[10]研究了多径效应对全球卫星定位系统三频信号的影响;文献[11]拟合了北斗三号卫星信号随机模型,评估了BDS和GPS组合系统模糊度解算性能和定位精度;文献[12]针对电离层延迟和对流层延迟误差进行参数估计,提出了一种部分模糊度固定的算法。
近年来,诸多学者的研究工作集中于北斗系统的卫星轨道、随机模型、多径效应和RTK中长基线解算,大部分是基于北斗二号卫星导航系统,对于北斗三号卫星导航系统在RTK短基线下的性能评估和改进相对较少。笔者基于包括北斗三号系统在内的所有BDS信号和GPS信号,提出了考虑大气环境差值影响的双差模型,并融合物体运动模型和卫星信号模型,提高RTK在复杂环境下的定位性能,评估组合系统和单系统在RTK短基线下的定位精度。
1 理论基础
RTK的基本原理是通过网络实时将基准站的伪距信号、载波相位信号以及精确坐标等信息传给移动站,移动站根据基准站观测值和自身观测值构建双差模型,可以消除接收机钟差、卫星钟差、硬件延迟、电离层影响、对流层影响以及其他公共影响因素,得到浮点解。再通过固定整周模糊度算法来获得固定解[13-14]。
1.1 双差观测模型
如图1所示的RTK双差模型中,基准站放置在位置已知的开阔地带,使用通信网络实时发送基准站的观测值。由于基线长度相对于接收机到卫星的距离非常微小,可以认为卫星j发射给移动站r和基准站b的信号经过了同样的大气环境,两者受到的电离层和对流层影响基本相同。
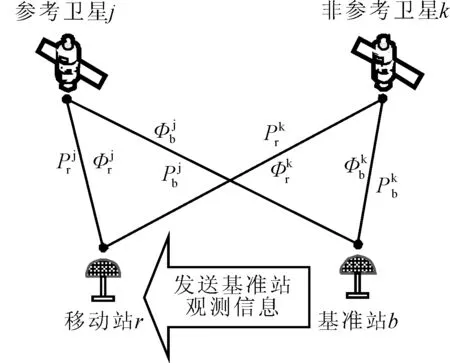
图1 RTK双差模型示意图
因此,移动站和基准站可以构建双差模型,消除电离层延迟、对流层延迟、卫星钟差、接收机钟差和初始相位偏差等公共因素影响。根据移动站和基准站观测值构建的伪距双差模型如式(1)所示。
(1)
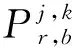
(2)
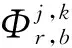
在伪距双差模型和载波相位双差模型中,接收机到卫星的距离受到Sagnac效应的影响。其计算方式不能直接使用信号发射时刻接收机和卫星在地心地固坐标系下的坐标计算,需要考虑在信号传播过程中地球自转引起的参考坐标系变化。因此,在考虑Sagnac效应后,接收机r到卫星j的几何距离如式(3)所示。
(3)
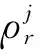
1.2 整周模糊度固定
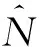
(4)
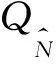
(5)
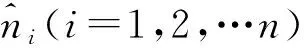
(6)
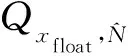
2 RTK短基线处理及改进策略
北斗卫星导航系统是全球唯一全星座播发三频信号的导航系统,充分使用BDS的B1、B2、B3频段和GPS的L1、L2、L5频段信号来解算位置,可以极大提高定位精度。在使用双差模型求解接收机的位置之前,需要获得接收机的近似位置,减少后续迭代计算量,快速找到收敛位置。研究中使用观测历元内的L1/B1频段伪距观测数据求解近似位置信息,作为双差观测模型求解的初始值。
2.1 伪距单点定位
伪距信号主要受到接收机钟差、卫星钟差、电离层和对流层影响,因此建立的伪距信号模型如式(7)所示。
(7)
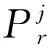
研究中使用伪距信号模型求解接收机的近似位置时,电离层采用Klobuchar模型计算延迟改正参数。该模型是由Bent电离层经验模型简化而来,在北半球中纬度地区的平均改正有效率达到50%以上[16]。对流层采用Saastamoninen模型,在提供较为准确的气象数据时,该模型计算的干延迟分量精度可达到亚毫米级,而湿分量延迟由于大气中水汽含量变化难以准确计算,大部分模型计算误差都比较大[17]。卫星钟差采用广播星历提供的改正参数计算得到,但是由于卫星运行速度与接收机运行速度差异,且两者所在引力位不同,需要考虑狭义相对论和广义相对论带来的时间偏差,改正后的卫星钟差模型如式(8)所示。
(8)
式中:dtj为卫星j的钟差;a0、a1、a2为广播星历提供的卫星钟差改正模型参数;tk为广播星历拟合时长;G为地球引力常数;M为地球质量;a为地球长半轴。
由于卫星高度角、信噪比等因素造成信号观测质量不同,每个卫星构建的伪距信号模型误差也不同,因此赋予每个伪距观测方程不同的权重,可以得到误差更小的解。使用加权最小二乘法(weighted least squares,WLS)求解伪距信号模型,每个观测方程的方差数据由卫星高度角、伪距信号信噪比、电离层模型改正误差、对流层模型改正误差、导航系统误差和伪距测量误差等因素共同决定。由以上分析得到伪距单点定位处理方法如图2所示。
算法1:伪距单点定位处理算法
输入:单历元内L1/B1频段伪距观测值obs.P[n];广播星历信息brdc
输出:移动站伪距单点定位计算结果roveriter
(1) iter ← 0; Δx←[0 0 0];roveriter←[0 0 0];
(2) while iter < 10 or ||Δx||2>1e-4
(3) for m ← 1 to n
(4) 从brdc选取obs.P[m]所属卫星m的最佳广播星历数据nav
(5) 基于广播星历nav的16参数,计算卫星m发射信号时刻的位置、速度
(6) 根据式(8),计算卫星m的钟差
(7) 根据klobuchar模型和Saastamnoinen模型计算接收机迭代位置到卫星m的电离层延迟和对流层延迟
有些学生为了达到美化的目的,在绘图手段上花费的时间过多;也有的为了“可视化”而“可视化”,置换了一些更好的教学方法,得不偿失。所以,教师要注意,教无定法,在中考复习中“思维可视化”只是一种策略、一种手段,不是替代当前的教学方法,而是与之相适应、相配合。只有让“思维可视化”与“中考复习”和谐地融为一体,促进学生对科学本质的理解,才能使凝固的课堂重新焕发出生命的活力,才能在这场没有硝烟的中考复习战中获胜。
(8) 计算WLS算法中矩阵H、残差矩阵v和权重矩阵W的第m行元素
(9) End for
(10) 计算迭代增量Δx=(HTWH)-1HTWv
(11) 更新移动站迭代位置roveriter←roveriter+Δx
(12) iter ← iter + 1
(13) End while
图2 算法1
2.2 改进双差模型
随着基线的延长,移动站和基准站所处大气环境存在差异,因此带来的电离层、对流层影响不能完全通过双差模型消除。研究中考虑该因素对定位精度的影响,补偿基线延长时未完全消除的大气环境差值,重新建立伪距双差模型和载波相位双差模型分别如式(9)、式(10)所示。
(9)
(10)
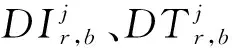
2.3 融合物体运动模型
笔者使用拓展卡尔曼滤波算法(extended kalman filter,EKF)融合物体运动模型和卫星信号模型,验证融合算法的有效性。使用该算法的前提条件是系统最优解区域可以用线性模型拟合,且模型测量服从高斯分布,即过程噪声和测量噪声服从高斯分布。其核心思想是不同测量模型得到的计算结果均服从高斯分布,这些模型的计算结果相乘后依然服从高斯分布,相乘后的高斯分布解即最优解。EKF算法主要分为预测和更新两个部分。其中,EKF算法预测部分如式(11)所示。
(11)
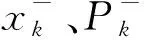
(12)
(13)
式中:[rr(k)vr(k)ar(k)Nr,b(k)]T为k时刻的待求未知量;rr(k)、vr(k)、ar(k)分别为接收机在地心地固坐标系下的三维位置、速度、加速度坐标,Nr,b(k)为双差模型中三个频段的单差模糊度;[rr(k-1)vr(k-1)ar(k-1)Nr,b(k-1)]T为k-1时刻求解出来的未知量状态;I为单位矩阵;dt为采样间隔。
双差模型中使用的EKF更新部分如式(14)所示。
(14)
式中:Kk为EKF增益;R为测量误差矩阵,由卫星高度角和信号信噪比决定;I为单位矩阵;yk为测量值,由三个频段载波相位双差值和伪距信号双差值构成,如式(15)所示。H为状态观测矩阵,可由伪距双差模型和载波相位双差模型推导得到,如式(16)、(17)所示。
(15)
(16)
(17)

综合以上分析,基于改进后的双差模型,使用EKF算法融合物体运动模型,求解固定解的处理方法如图3所示。

3 实验结果及分析
3.1 实验设备及方案
实验设备主要为长沙海格北斗信息技术有限公司自主研发的DB503D全系统全频点高精度定位定向板卡、配套天线、个人笔记本电脑以及移动电源,主要设备如图4所示。

图4 实验主要设备
实验中一台接收机放在位置已知的开阔地带作为基准站,另一台接收机固定在车辆顶部作为移动站。两台接收机由两个移动电源独立供电,采集多种环境下的卫星数据,用以验证改进算法的实际定位性能,对比算法改进前后对位置精度的影响。
3.2 改进后的双差模型验证
大气环境差值对定位结果的影响与基线长度相关,基线越长,该影响因素所占比重越大。因此,为验证改进后双差模型的可行性和性能,将实验基线长度控制在13 km左右、实验时间设置为一天、采样频率设置为30 s。在该条件下,移动站保持不动,分别对比改进双差模型前后的解算情况,两种情况下的解算结果在E、N、U三个方向的标准差如图5所示。
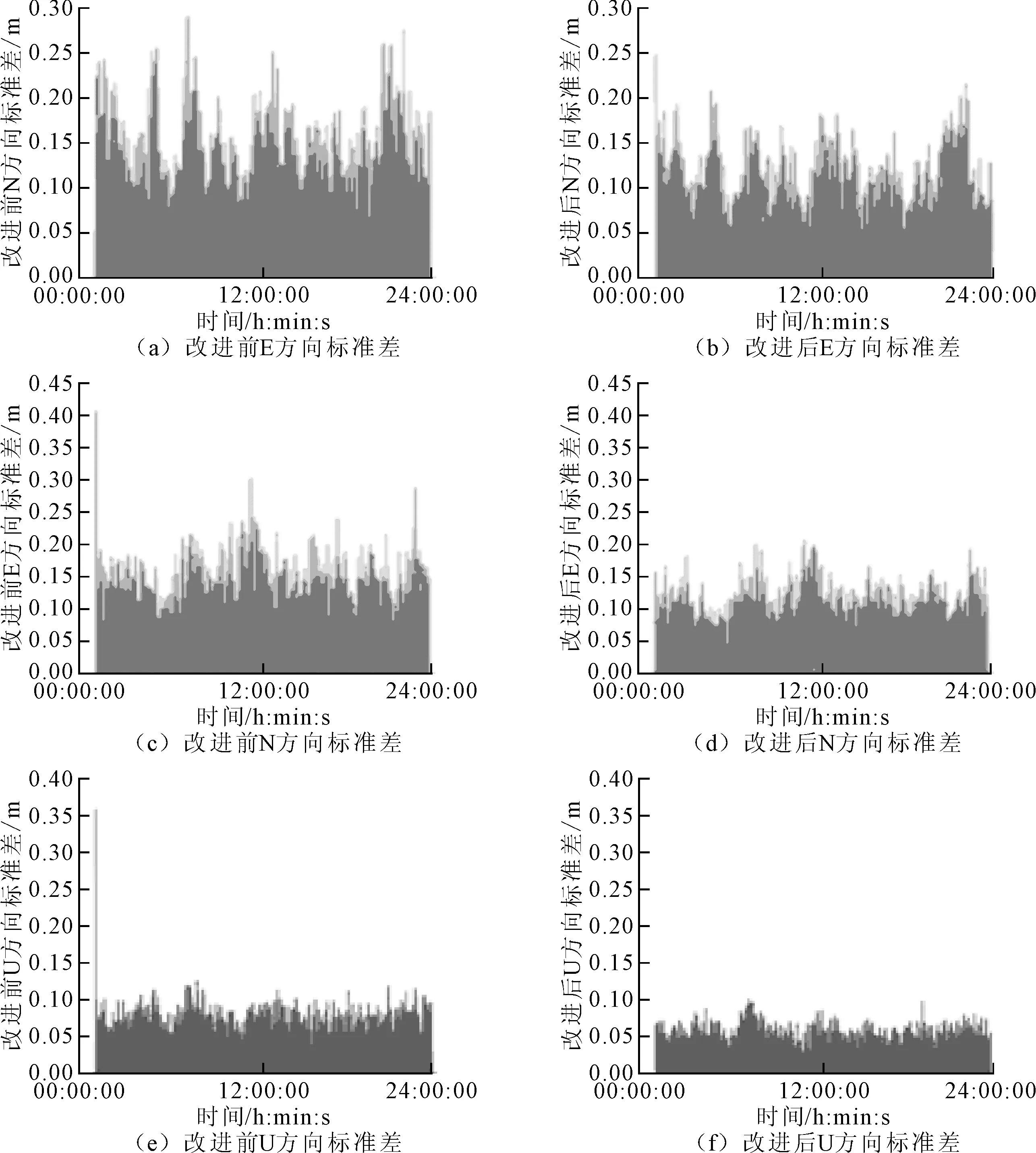
图5 改进双差模型前后对比
由图5可知,改进后的双差模型在E、N、U三个方向的标准差均有减小,可以在一定程度上补偿大气环境差值影响。在三个方向上的平均标准差、最大标准差和均方根误差(root-mean-square error,RMS)的具体变化如表1所示。
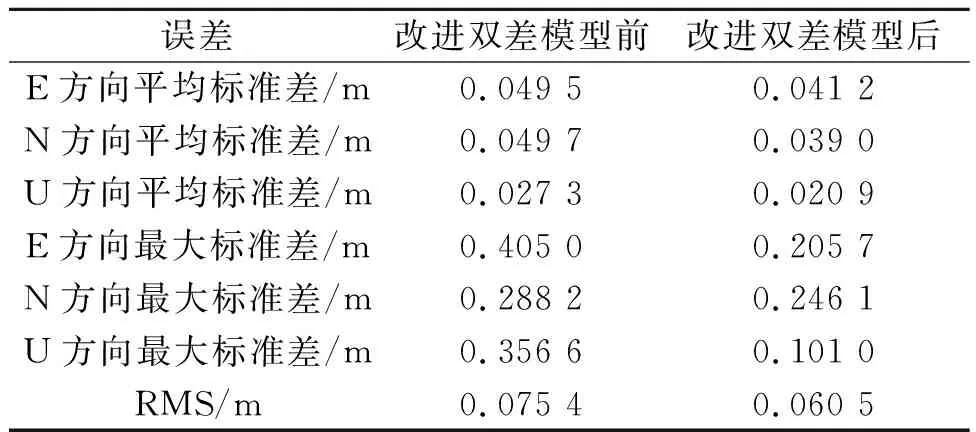
表1 改进双差模型前后解算结果对比
由表1可知,改进后的双差模型在E、N、U三个方向平均标准差、最大标准差以及RMS值都有所减小,实验表明:改进后的双差模型可以减弱基线长度带来的大气环境差值影响,但是减小比例相对较小。分析该影响因素的具体作用方式可知,该因素对定位结果精度影响所占比重与基线长度呈正相关,随着基线继续延长,改进后的双差模型可以获得更高的位置精度。
3.3 对融合物体运动模型的验证
为验证融合物体运动模型后算法的定位精度,实验时间从2021年6月9日09:14:21开始到当天09:59:09结束,历时约45 min,实验中共视卫星数量变化如图6所示。
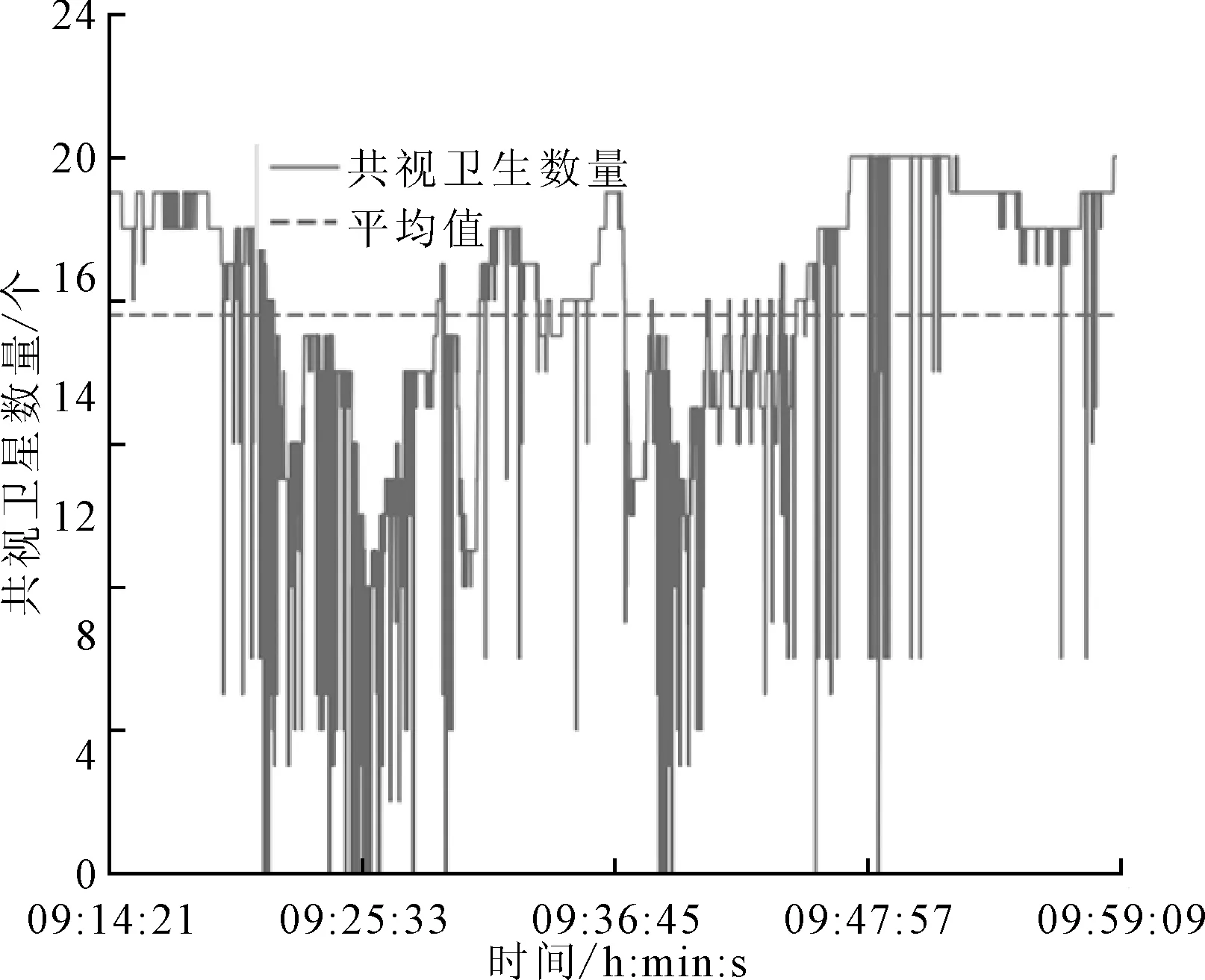
图6 共视卫星数量变化
由图6可知,整个实验过程中,可解算的共视卫星平均值为15.58颗,大部分时段的共视卫星在12颗以上。但是由于移动站所处环境改变,部分时段共视卫星数量剧烈变化,尤其是在09∶25∶33附近。由实验过程可知该时间段内移动站所处位置附近存在高大建筑物,严重遮挡该方向卫星信号。在该实验所处的复杂环境条件下,对比融合物体运动模型前后,解算结果在E、N、U三个方向的标准差如图7所示。
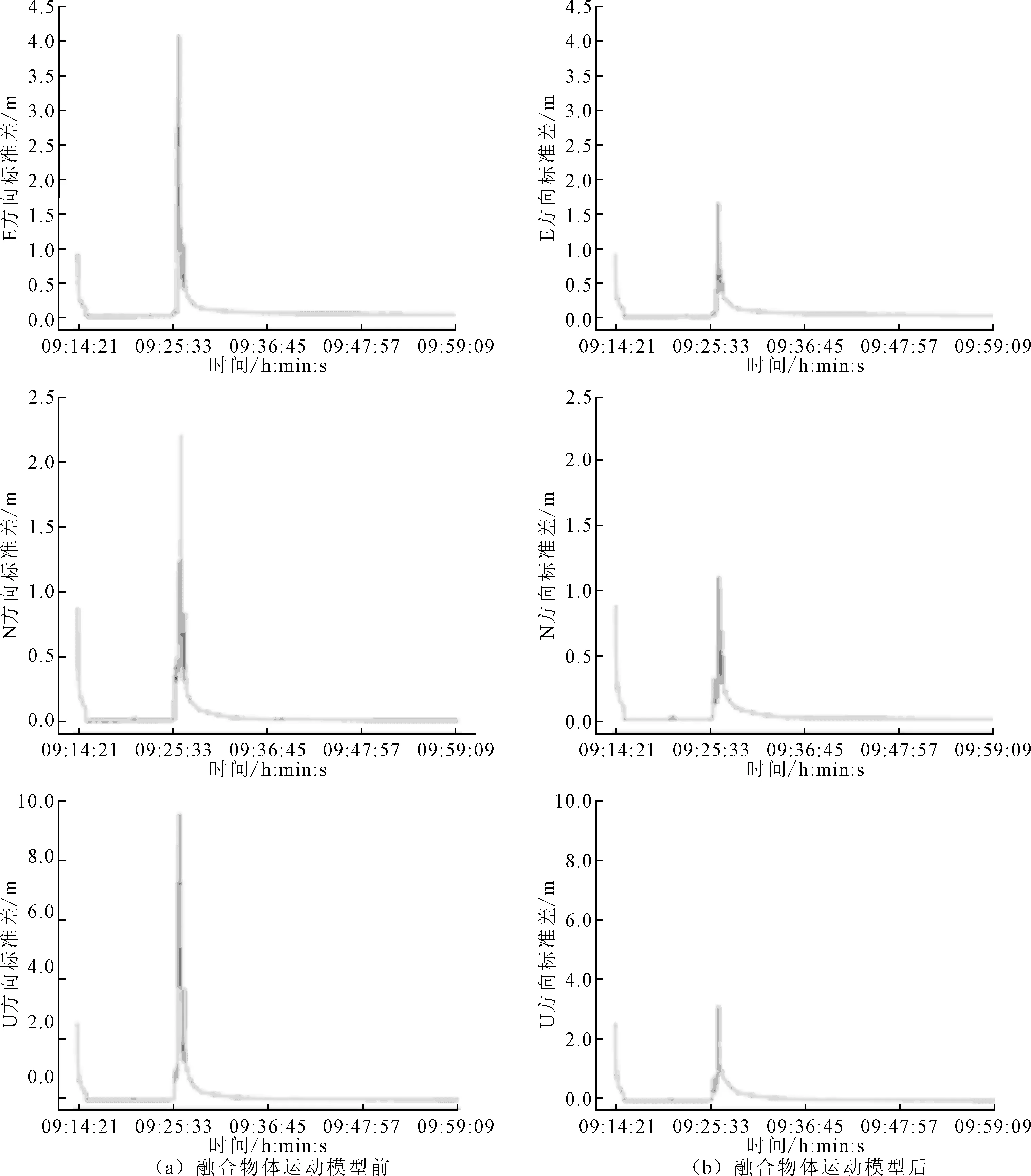
图7 融合物体运动模型前后对比
由图7可知,当移动站所处环境复杂,接收到的卫星信号较少,即在09∶25∶33附近的时间段内,RTK解算效果较差,出现4 m左右的定位偏差。但是融合物体运动模型后,该时段内的解算结果比原始RTK算法定位误差小,且在其他卫星信号正常阶段与原始算法定位差别较小。两种方式下在E、N、U三个方向的平均标准差、最大标准差和RMS值具体变化如表2所示。
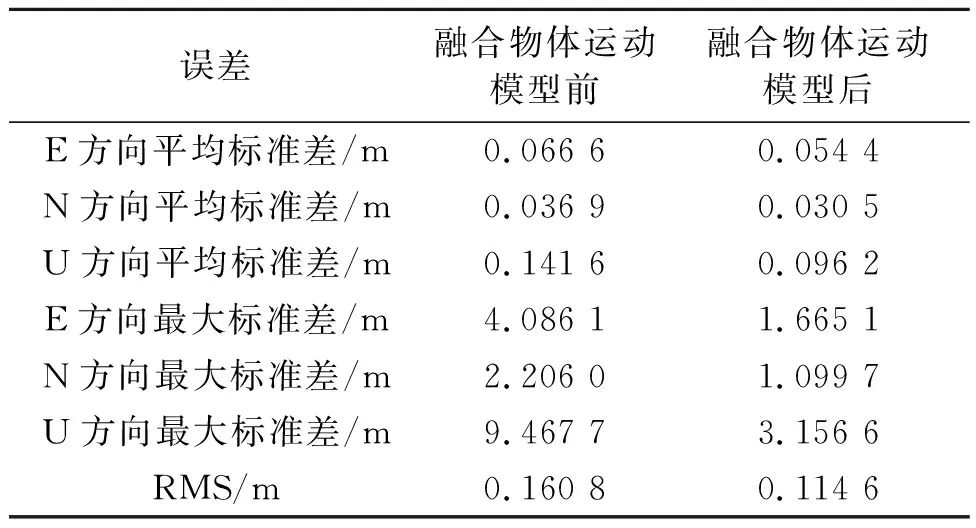
表2 融合物体运动模型前后位置精度对比
由表2可知,融合物体运动模型后的解算结果在E、N、U三个方向的误差数据都有所降低。实验证明改进后的定位算法可以在卫星信号较差时,减小定位误差、提高定位精度、提升整体定位性能。为进一步验证物体运动模型对定位结果的改善,结合地图查看实际定位效果,两种方式下的定位结果如图8所示。

图8 实际定位结果对比
图8所示路线为实验中09∶25∶33附近时段解算结果,从上到下依次为线条A、B、C,其中线条A为实际行驶路线,线条B为融合物体运动模型后的解算结果,线条C为融合物体运动模型前的解算结果。对比两种方式下的解算结果,线条B更符合实际行驶路线,定位误差较小。因此在融合物体运动模型后,可以有效提高RTK在复杂环境下的定位精度。
3.4 组合导航系统与单系统对比
中国的BDS、美国的GPS、欧盟的伽利略导航系统(Galileo satellite navigation system,GALILEO)和俄罗斯的全球导航系统(global navigation satellite system,GLONASS)是比较成熟的几种全球卫星导航系统。在中国大部分地区,接收到的GLONASS卫星信号最少,该系统主要为高纬度地区服务,其次为GALILEO卫星信号,而BDS和GPS系统相对较多。因此,BDS + GPS是效率相对较高的组合系统之一,可以解决部分复杂环境下单系统信号过少而无法定位的情况。
实验选取包括北斗三号卫星在内的全部BDS信号和GPS信号,实验路线选择经过高大建筑物附近,测试复杂环境下组合系统定位性能,对比北斗系统和组合系统定位精度。实验时间为2021年6月9日,其中可用于单系统和组合系统RTK解算的共视卫星数量变化如图9所示。
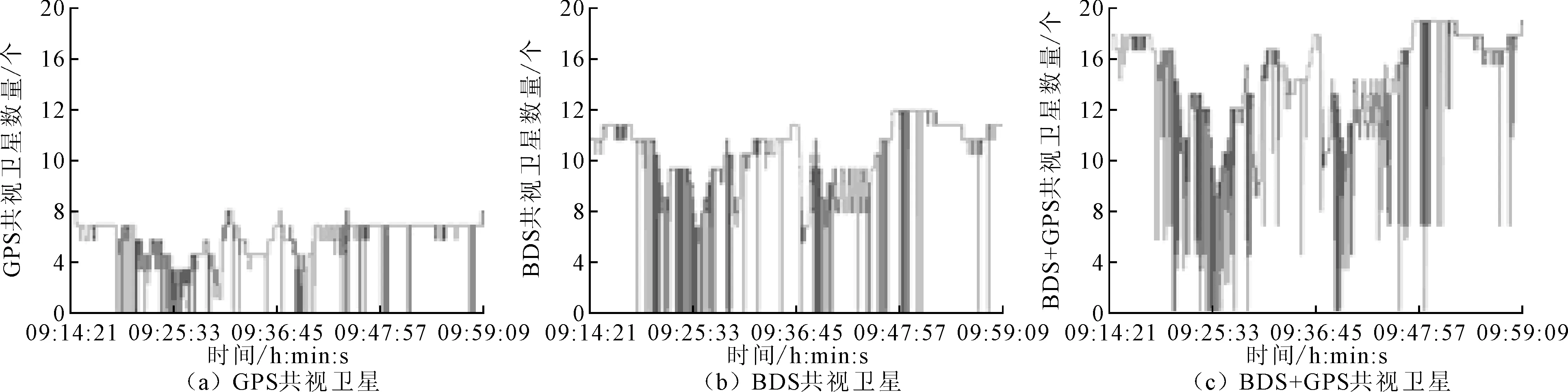
图9 共视卫星数量变化
由图9可知,受移动站所处环境变化,存在部分路段共视卫星数量剧烈变化。其中,GPS共视卫星平均保持在5颗左右,BDS为10.5颗左右,组合系统为15.5颗左右。使用改进后的算法分别解算单系统和组合系统数据,对比解算结果,BDS、GPS和BDS + GPS组合系统解算结果分别如图10(a)、(b)、(c)所示。

图10 单系统与组合系统解算结果对比
由图9和图10可知,GPS单系统在复杂环境下的部分路段共视卫星不足4颗,不能保证RTK的实时解算,存在部分路段无解,且定位漂移严重,如图10(a)中的A、B两地。相对于GPS严重的定位漂移和无解路段,BDS单系统在整个实验过程中基本没有无解路段,解算结果与实际行驶路线比较符合,但是BDS在图10(b)中的C地,定位结果偏移实际行驶路线。造成该现象的主要原因是该地高建筑物导致卫星信号实际传播路径不是沿直线传播,带来了较大的多径效应。而组合系统由于较多的卫星信号,可以降低建筑物遮挡和多径效应的影响,无论是在A、B、C任何一个地点,都极大改善了单系统定位的缺点,定位结果符合实际行驶路线,定位偏差较小。其中,单系统和组合系统在E、N、U三个方向的标准差变化如图11所示。
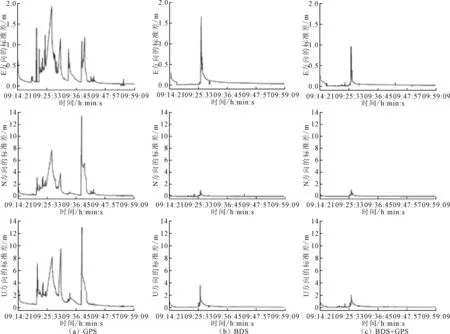
图11 单系统与组合系统对比
GPS单系统在整个实验过程可使用的平均共视卫星仅为5颗,因此在图11三个方向的标准差都相对较大。而BDS单系统或组合系统平均共视卫星在10颗以上,可以得到相对较好的定位结果,两者差别相对较小。但是当移动站处于相对复杂的环境中,如09∶25∶33附近,使用组合系统可以减弱部分卫星信号的多径效应影响,得到相对较好的定位结果。单系统和组合系统在E、N、U三个方向的平均标准差、最大标准差和RMS的具体变化如表3所示。
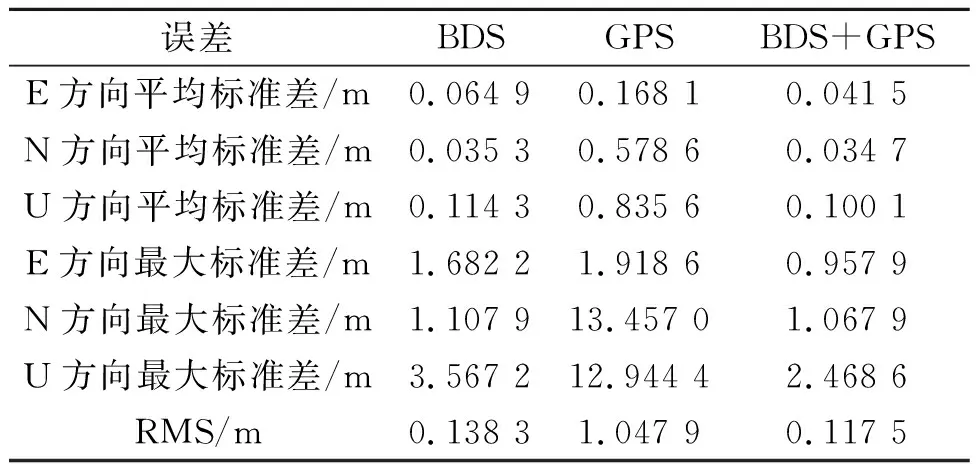
表3 单系统与组合系统定位精度对比
由表3可知,组合系统在E、N、U三个方向的数据均优于单系统定位结果。实验表明GPS系统不能较好地应对复杂环境下的高精度定位任务,而北斗系统定位性能相对优越,大部分情况下解算性能和组合系统接近。但是使用组合系统可以在复杂环境下降低信号遮挡和多径效应,获得比单系统更高的定位精度,提升整体定位性能。
4 总结
笔者基于RTK技术,使用伪距信号、载波相位信号建立双差观测模型,消除了电离层、对流层、接收机钟差和卫星钟差等因素影响,进行了复杂环境下RTK定位精度的实验验证。通过上述实验及数据分析,得出以下结论:
(1)随着基线增长,大气环境影响因素比重增加,使用新双差模型,可以降低基线长度引起的定位误差。
(2)使用EKF算法融合物体运动模型和卫星信号模型,可以充分利用上一时刻的有效数据,降低复杂环境下较差的卫星信号影响,提高观测质量不佳路段的定位精度,提升整体定位性能。
(3)使用BDS+GPS组合导航系统可以增加实时解算的共视卫星数量,降低多径效应影响,提高遮挡严重地区的定位精度。
