战斗部侵彻多层建筑物定位算法与仿真验证

李建昌，马 林，刘建荣，王艳艳

(中国兵器工业试验测试研究院， 陕西 华阴 714200)

1 引言

随着实战化考核的深入开展，武器装备交付由“交设备”向“交能力”的逐步转变，其对靶场试验及测试方法也提出新的更高要求。诸如钻地侵彻战斗部对多层建构筑物侵爆试验中，其侵彻轨迹、起爆位置、毁伤效果，是侵爆类战斗部能力考核的关键指标。但受侵彻过程烟尘、火光、建筑物/构筑物结构遮挡及侵彻后结构稳定性影响，试验中光测缺乏测试环境、试验后现场测量具有潜在不安全因素，现有轨迹测量和目标定位手段无法有效实施。针对此问题提出基于振动信号解算战斗部侵彻多层建筑着靶点的方法，根据战斗部侵彻过程目标内部产生的振动参量，构建振动参量测试系统，研究分析不同布点阵列和解算方法特点，利用战斗部侵彻多层建筑物过程中产生的振动信号，解算出着靶点位置，分析对比了不同布点方案和定位算法优劣，为侵爆类战斗部毁伤参量试验中安全快速测试及结果处理提供技术支撑。

2 定位算法

战斗部侵彻多层建筑物撞击点的定位属于平面定位问题，常用的平面定位算法有：根据振动信号传播时间(TOA/TDOA)的定位方法；根据信号强度(RSS)的定位方法；根据信号到达角度的定位方法(AOA)或信号达到方向的定位方法(DOA)；以及上述几种方法的混合使用。

基于三角阵列传感器对目标进行定位的理论主要有正三角和直角三角方法，该方法在利用地震波对震源进行探测中已具有一定的成熟度，但文献中给出的方法主要是针对无限空间区域，即目标点至传感器的距离远远大于传感器之间的距离的情况，而不适合运用于战斗部侵彻多层建筑物等有限空间的情况。

本文对传统的TDOA算法、单直角阵列定位算法以及双直角阵列定位算法进行了推导，补充完善了相关文献中计算公式的省略项，使算法的实现能够满足类似多层建筑物等有限空间内目标的定位问题。

2.1 TDOA定位算法

如图1所示，目标点(，)为待定撞击点位置，观测点1(，)，观测点2(，)和观测点3(，)为3个传感器的安装位置，设3个观测点到目标点的位置分别为，和，距离差Δ是观测点1之后的各个观测点至目标点的距离与观测点1至目标点的距离差，=1，2，…。则有：

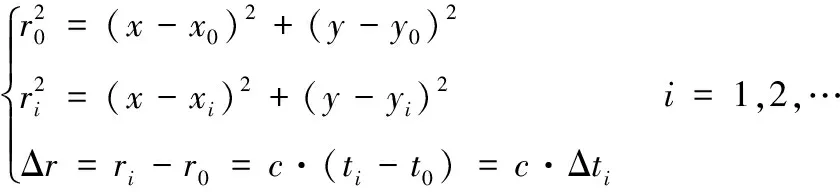
(1)

由式(1)可得：

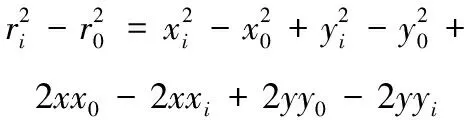
(2)

又因：

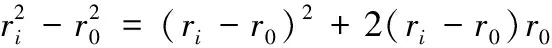
(3)

将式(1)、式(3)代入式(2)化简后得：

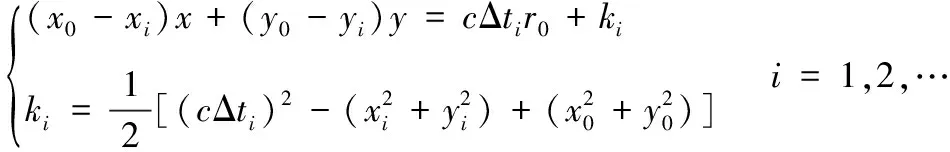
(4)

式(4)中： Δ、、、、为已知量，为介质内振动波的传播速度，可以通过测试的方法获得，只有、和为未知量。通过Taylor算法、NewTon算法、遗传算法、直接求解算法等算法对式(4)进行求解，即可获得撞击点的位置坐标。

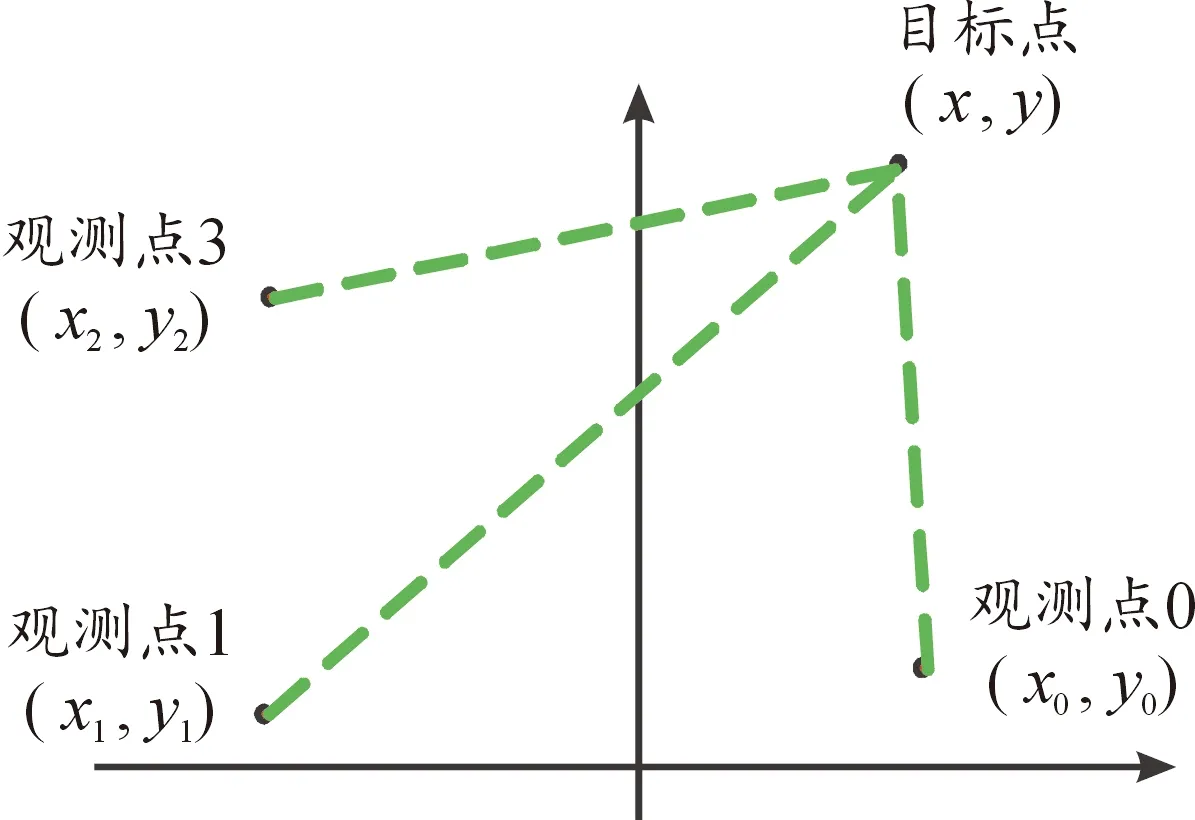
图1 TDOA定位算法原理示意图

2.2 单直角阵列定位算法

单直角阵列定位原理如图2所示。直角三角阵列的传感器测点坐标分别为：(0,0)、(,0)、(0,)，目标点坐标为(,)，目标点到各个测点的距离分别为：、、，目标点与观测点1的夹角为，观测点1、2之间的距离为，信号达到时间差为Δ，观测点1、3之间的距离为，信号到达时间差为Δ，以观测点1作为局部坐标系原点，则有：

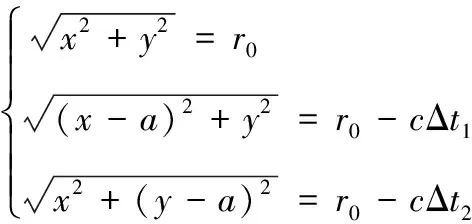
(5)

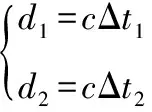
利用Matlab解符号方程组的功能解此方程组并整理可得：

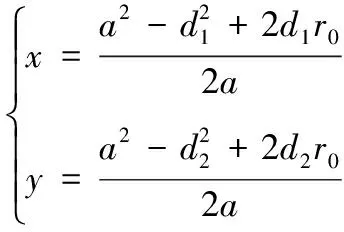
(6)

其中：

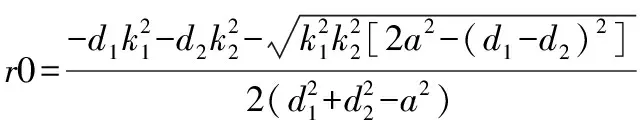
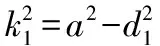
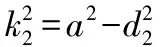
从而

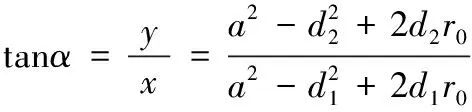
(7)

对于无限平面内，由于>>和，此时式(7)可近似为

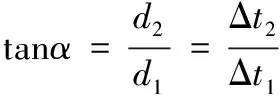
(8)

但对于有限空间(如建筑物内部)，由于不满足的条件，式(7)将不可以进行上述近似。

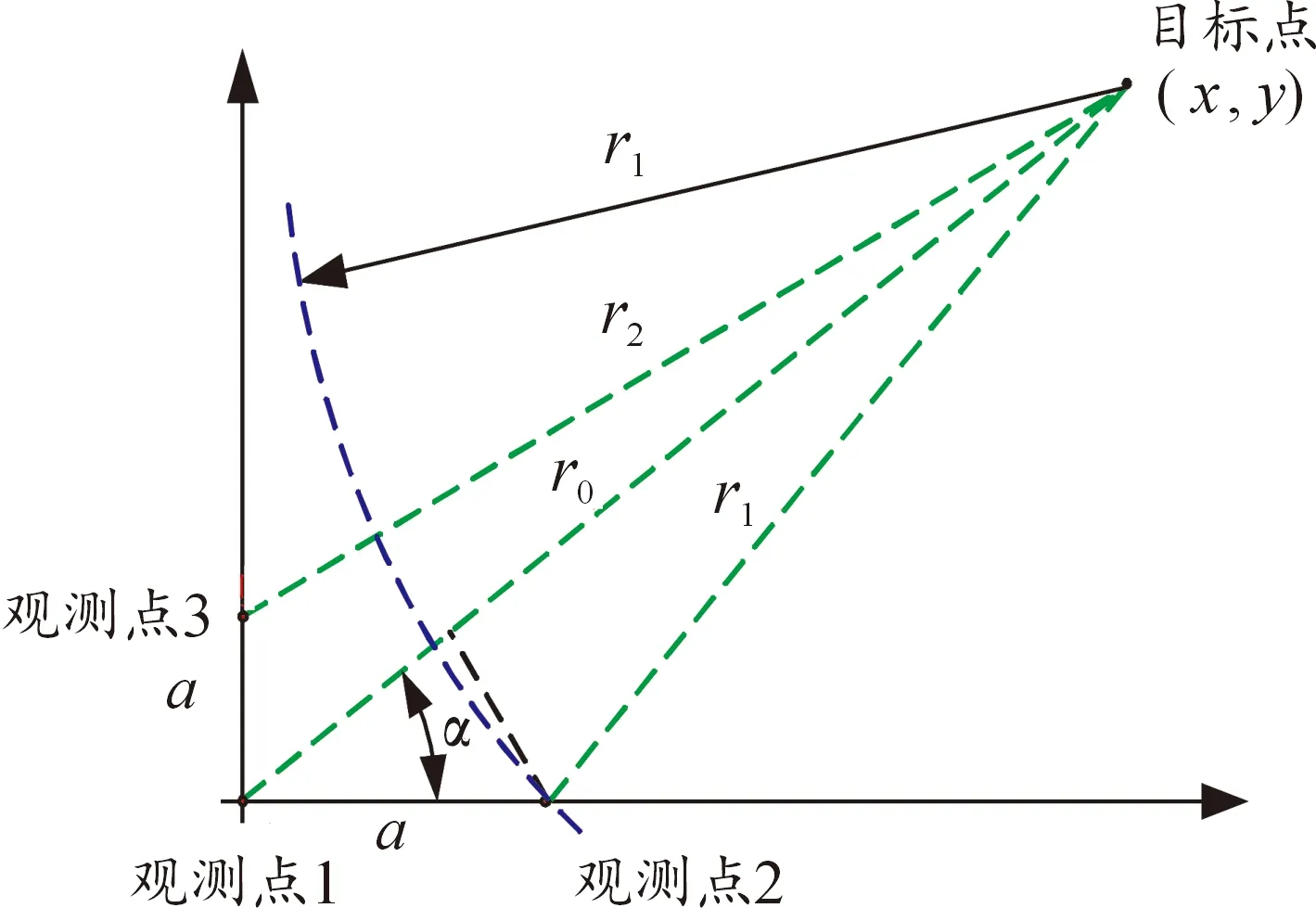
图2 单直角阵列定位算法原理示意图

2.3 双直角阵列定位算法

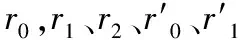
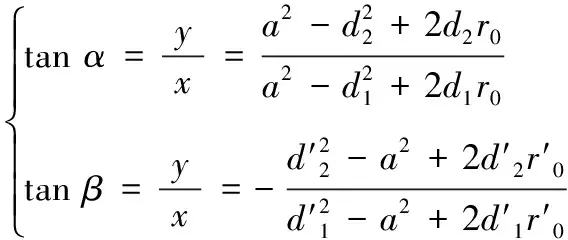
(9)

对于无限平面内，由于>>和，此时式(9)可近似为

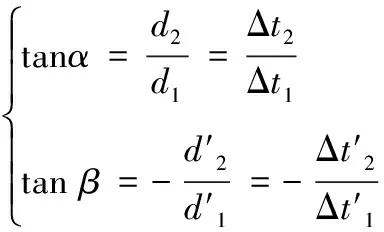
但对于有限空间(如建筑物内部)，由于不满足的条件，式(9)将不可以进行上述近似。

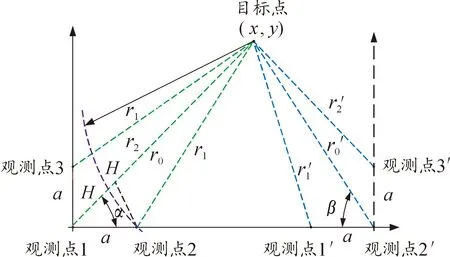
图3 双直角阵列定位算法原理示意图

同时，依据图3所示的三角关系有：

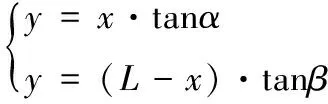
(10)

通过对式(10)的求解可得：

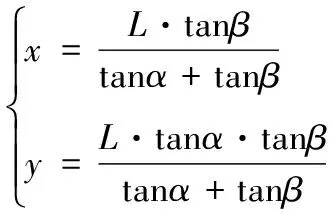
(11)

式(11)中参数由、和，其中为已知量，只需通过式(9)求出和便可实现对目标点的定。

3 定位误差分析

3.1 TDOA定位误差分析

运用TDOA定位算法进行目标定位时，不同的定位系统对不同空间位置的目标进行定位精度是不同的，即目标位置的定位误差与目标相对于定位传感器的几何关系是密切相关的。为了描述定位误差与几何位置的关系，常用的定位精度分析计算方法有GDOP(geometric dilution of precision)和CRLB下界的方法。关于这2种计算方法的具体步骤相关文献中均有较为详实的描述，本文就不展开谈论，若有需求，可查阅相关技术文献。

3.2 单直角阵列定位误差分析

..定位坐标的误差分析

通过对式(6)求导，可得：

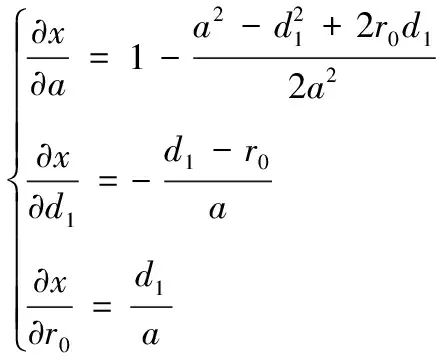
(12)

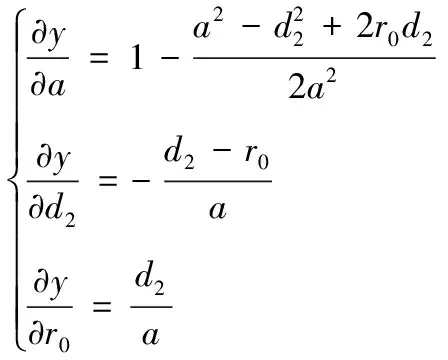
(13)

从式(12)、式(13)可以看出：运用单直角阵列对目标进行定位时，定位结果不仅与布阵参数有关外，而且随着定位距离的增大，目标点定位误差也在增大。

通过误差合成可得、方向的定位误差分别为

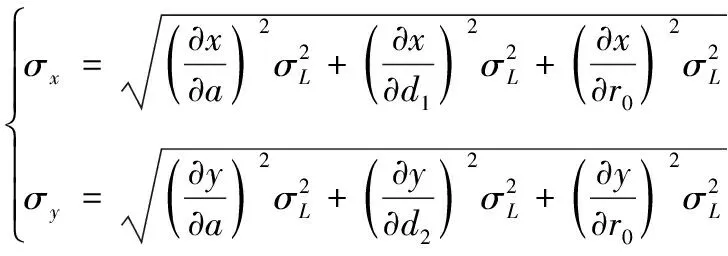
(14)

其中为测距误差。

定位角度的误差分析

通过对式(7)求导可得：

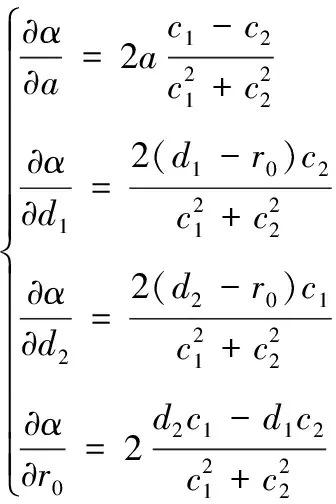
(15)

其中：

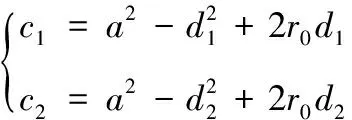
当时，式(15)可简化为

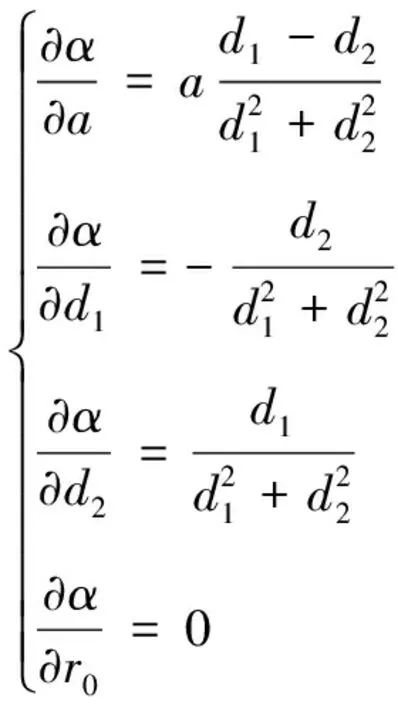
(16)

从式(16)可以看出：当>>、和时，定位距离对定位角度无影响。

通过误差合成可得定位角度误差为

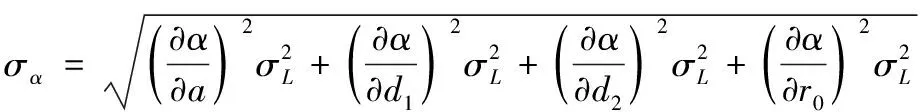
(17)

其中为测距误差。

3.3 双直角阵列定位误差分析

通过对式(11)求导，可得：

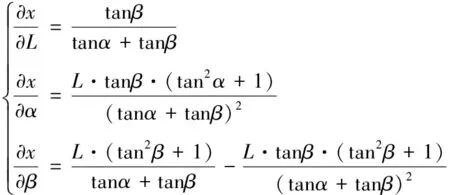
(18)

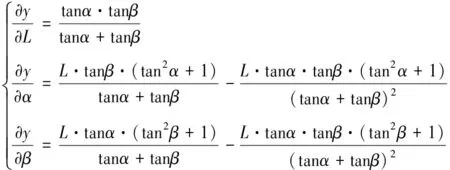
(19)

通过误差合成可得、方向的定位误差分别为：

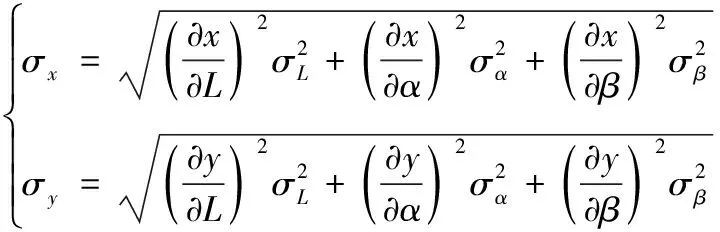
(20)

其中为测距误差，为定位角度误差，可由322中所示方法获得。

通过对式(18)—式(20)的分析结合3.2.2定位角度误差分析可以得出：采用双直角阵列定位算法进行定位时，定位精度受传感器的精度以及布阵精度的影响，并不像单直角阵列算法那样受落点定位距离的影响。

4 精度验证

为了对3种算法的定位精度进行验证，建立了某型战斗部侵彻两层框架结构的钢筋混凝土建筑物有限元仿真分析模型(图4)，其中，主体框架结构采用六面体单元和混凝土材料，钢筋采用与混凝土共节点的beam单元和弹塑性钢材料。在建筑物每层表面各添加6个观测点，构成2个直角三角形阵列，获取战斗部侵彻过程中产生的振动参量传递至各个观测点处的信号特征(获取的典型信号特征如图5所示)，通过对曲线的判读获得相关时间信息，结合观测点的位置信息，运用上述3种算法得到的定位结果如表1、表2所示。

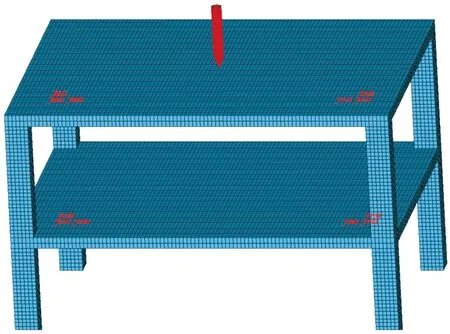
图4 仿真分析模型示意图

图5 获得的典型振动加速度曲线

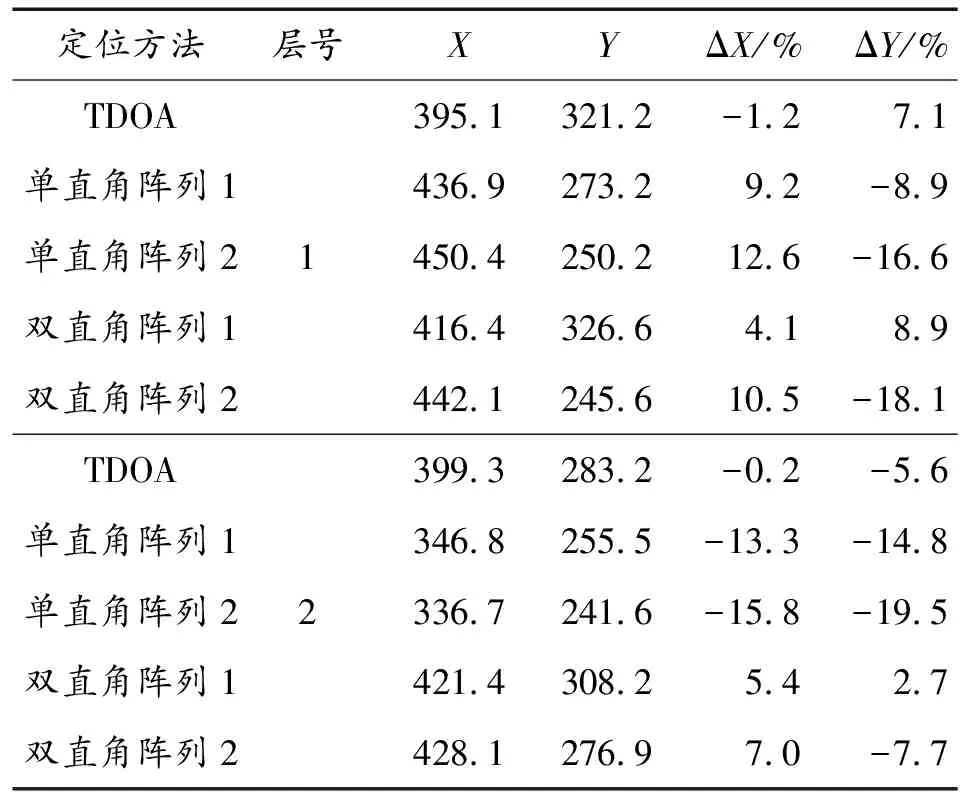
表1 定位结果(cm)

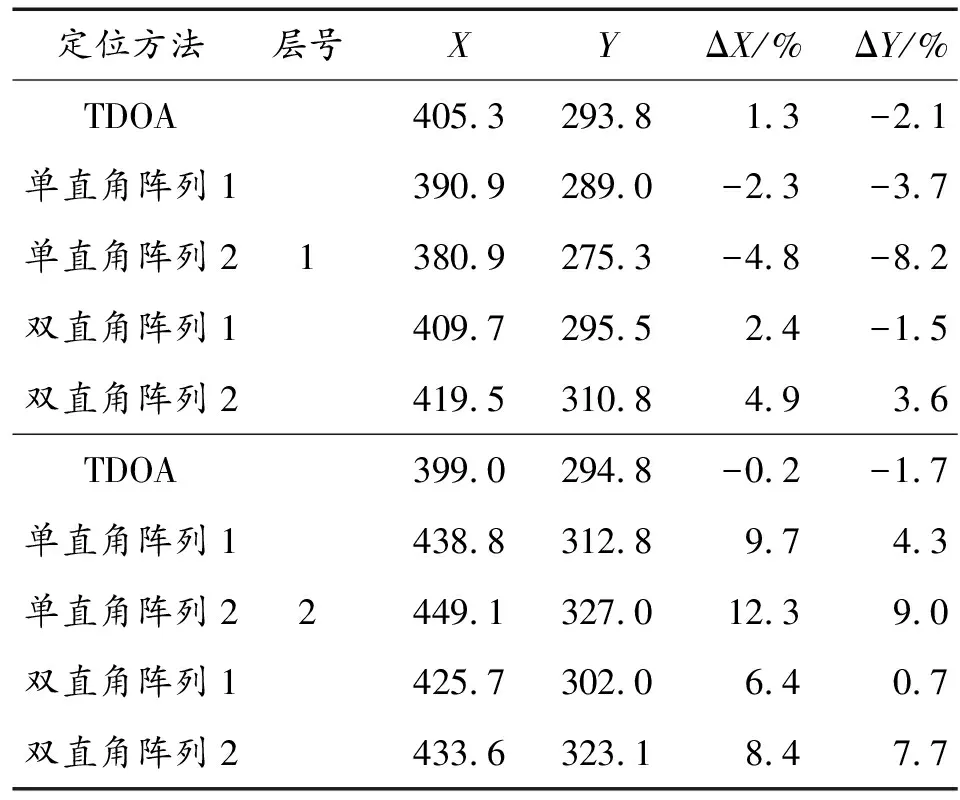
表2 定位结果(cm)

通过对表1、表2中数据分析可知：

1) TDOA算法的计算结果与真实值的偏差最小，双直角阵列定位算法的计算结果次之，单直角阵列定位算法的计算结果与真实值的偏差最大；

2) 本文中推导公式与常用简化公式相比较，能够较好地提高计算结果的定位精度；

3) 单直角阵列定位算法对时间判读精度的要求较高，即单直角阵列算法的容错性较差；TDOA算法和双直角阵列定位算法能够很好的克服单直角阵列算法缺陷，能保持较高的定位精度。

5 结论

在对TDOA定位算法、单直角阵列定位算法、双直角阵列定位算法3种定位算法定位原理推导的基础上，分析了2种直角阵列算法的定位误差；结合有限元仿真分析获得战斗部侵彻多层框架结构建筑物过程中产生的振动加速度数据对3种定位算法的定位结果进行了验证，最终表明：本文推导的计算关系式能够解决战斗部侵彻多层框架结构建筑物过程中各楼层目标撞击点的定位问题。

本文的分析结论能够为今后开展有限空间及框架结构建筑物内部目标定位方面试验、定位数据分析提供技术支撑。