具有非局部源双重退化抛物方程解爆破时间下界的估计

吴秀兰，杨晓新，吴彦锐

(1.长春理工大学 数学与统计学院，吉林 长春 130012；2.长春大学 电子信息工程学院，吉林 长春 130012)

1 预备知识

考虑具有非局部源双重退化的抛物方程

(1)

其中：Ω⊂Rn(n≥3)是具有光滑边界的有界区域；p>2；m≥1；初值u0(x)是在Ω上的非负连续函数.当m=1时，F.C.Li和C.H.Xie[1]借助上下解的方法得到了问题(1)局部解的存在唯一性，并且证明了当指标q>p-1，且初值充分大的条件下，解在有限时刻爆破.非线性发展方程(1)刻画了物理、化学和生物种群动力学中的很多现象，而且更加符合实际.近年来，国内外许多学者对方程解的爆破与熄灭现象都展开了研究[2-4].当m=1时，文献[5-8]分别给出了方程解存在性和唯一性，与解的爆破条件和熄灭条件.在生活中解的爆破时间的下界可以给出一个安全的操控时间，对解爆破时间下界估计具有十分重要的意义.关于解爆破时间下界的估计的研究也取得了一系列的研究成果[9-12].特别地，文献[9]给出了空间维数n=3时，具有非局部源p-Laplace方程解爆破时间下界的估计.受到已有研究成果的启发，本文运用微分不等式技巧，针对空间维数n≥3给出问题(1)解爆破时间下界的估计，推广并完善已有的结果[9].

2 主要结果

定理1假设2m(p-1)，若函数u(x，t)是问题(1)在有界区域Ω⊂Rn(n≥3)上的非负弱解，定义函数

其中参数k满足

如果函数u(x，t)在φ(t)意义下有限时刻T爆破，那么T有下界

其中：

k1=km1|Ω|2，

结合问题(1)第一个方程

进一步有

令

利用待定系数法，有

(2)

对式(2)中第二项应用Hölder不等式得

(3)

结合式(2)—(3)有

(4)

对式(4)中的第二项应用Hölder不等式有

(5)

其中：

结合式(4)—(5)，进一步有

(6)

对式(6)中的第三项应用Schwarz’s不等式，有

(7)

由Sobolev嵌入不等式

W1，p(Ω)

有

(8)

结合式(7)—(8)，并应用带ε的Young不等式有

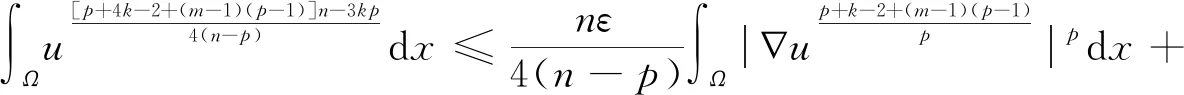
(9)

其中ε是待定常数.结合式(6)和(9)，有

令

k1=km1|Ω|2，

选取ε>0使得k3=0.取

从而

(10)

对式(10)关于时间t积分，有

3 结语

本文通过构造辅助函数并结合微分不等式，给出了具有非局部源双重退化抛物方程解爆破时间的下界估计.可以通过构造适当的辅助函数，给出该问题解爆破时间的上界估计，从而进一步给出该问题解的生命跨度.