直角突变式钢吊车梁裂纹扩展及疲劳寿命研究

胡宝琳， 周 磊， 庄继勇， 徐 庆

(1.上海大学 土木工程系, 上海 200444；2.宝武装备智能科技有限公司, 上海 201900)

钢吊车梁是工业建筑中的一种承受循环载荷的结构构件，它的安全使用对工业建筑正常生产起着至关重要的作用。随着炼钢产业的迅速发展，钢吊车梁在工业建筑中大量使用，疲劳断裂是吊车梁破坏的主要形式[1]。尤其重级以及超重级工作制的变截面钢吊车梁，变截面附近破坏现象严重。为了确保钢吊车梁在使用过程中的安全可靠，及时准确找到裂纹源，检测出处于不安全状态的构件并预测吊车梁疲劳寿命已成为亟待解决的现实问题。

众多学者从多种角度对变截面钢吊车梁疲劳问题进行深入研究，魏国前等[2]针对焊接结构可能存在的短裂纹问题，基于断裂力学原理提出一种考虑短裂纹阶段的疲劳寿命预测方法，准确预测了圆弧式变截面钢吊车梁疲劳寿命。幸坤涛等[3]和杨佑发等[4]基于损伤采用动态疲劳可靠度模型对钢吊车梁的疲劳应力幅和疲劳强度进行研究。卢铁鹰等[5]对直角突变式钢吊车梁进行应力测试和疲劳性能试验研究，认为在直角突变式吊车梁疲劳破坏的起始点出现在端封板与插入板连接焊缝及其附近主体金属上，继续承受循环荷载作用后，插入板与腹板连接焊缝附近腹板主体金属出现裂纹。赵晓青等[6-7]对弯曲封板直角突变式钢吊车梁缩尺模型疲劳进行试验研究，以焊趾处结构应力作为统计参量，统计回归出该连接类型的疲劳强度S-N曲线，并采用壳单元模拟变截面钢吊车梁插入板端部疲劳裂纹扩展。

裂纹扩展过程的数值模拟在钢桥和航空应用领域已有大量的分析研究[8-10]，但从裂纹扩展数值模拟的角度对吊车梁疲劳性能的研究较少。本文从疲劳裂纹扩展过程出发，基于线弹性断裂力学进行三维裂纹扩展数值模拟，研究直角突变式钢吊车梁裂纹扩展特性，预测其裂纹扩展寿命，为钢吊车梁疲劳强度评估提供参考依据。

1 裂纹扩展理论数值应用

为评估直角突变式钢吊车梁的疲劳性能，基于断裂力学其进行三维裂纹扩展数值模拟并计算裂纹扩展寿命。

1.1 裂纹破坏准则

吊车梁变截面位置受力复杂，裂纹一般情况下不会沿着直线方向继续扩展，裂纹扩展角度随受载类型不断变化。常用的复合型断裂准则主要分以下两类：①以裂纹尖端的应力应变场为基础的最大周向应力准则和最小应变能密度准则；②以能量平衡为基础的能量释放率理论，如能量释放率准则。

本文依据最大周向应力破坏准则[11]进行复合型裂纹扩展分析，该准则假定：

(1)裂纹沿最大周向应力方向扩展，即垂直于最大周向应力方向；

(2)当最大周向应力达到临界值时，裂纹开始起裂扩展。

根据线弹性断裂力学，可以得到裂纹尖端附近的应力分量在极坐标下表达形式，由上述假定可以确定裂纹扩展方向

(1)

1.2 裂纹扩展寿命

1963年，Paris等[12]通过对大量疲劳试验数据进行分析，研究发现金属材料的疲劳裂纹扩展速率与应力强度因子幅值密切相关，并提出了著名的疲劳裂纹扩展速率方程式，即Paris公式

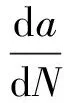
(2)

式中：a为裂纹深度或宽度；N为载荷循环次数；C和m材料常数，与材料的力学性质和试验条件有关；ΔK为应力强度因子幅值。

对Ⅰ型裂纹，根据Paris公式，可以对含裂纹构件进行疲劳裂纹扩展寿命评估，对式(2)进行积分，得到

(3)

式中：a0为初始裂纹长度，可由检测仪器或等效初始裂纹替代得到；ac为临界裂纹长度，可根据断裂判据或工程实际情况确定；Nc为裂纹由初始裂纹长度a0扩展至临界裂纹长度ac的应力循环次数，即裂纹扩展寿命(疲劳寿命)。

2 数值分析及验证

建立直角突变式钢吊车梁有限元模型，研究行车运行中变截面部位应力集中处主应力变化情况，取最危险细节引入初始裂纹进进行后续三维裂纹扩展数值模拟，将裂纹扩展寿命计算结果作为钢吊车梁疲劳寿命，并验证该方法的可行性与合理性。

2.1 有限元模型

采用ABAQUS有限元软件对直角突变式钢吊车梁建立整体有限元模型，吊车梁各截面参数如图1所示。行车移动时的轮压采用移动荷载进行模拟，研究吊车梁在移动荷载作用下各处应力峰值及变化情况，确定直角突变式钢吊车梁危险截面位置。

图1 直角突变式钢吊车梁截面参数Fig.1 Cross section parameters of right angle mutation type steel crane runway girder

2.1.1 移动荷载有限元模型建立

吊车梁钢材的应力-应变关系采用线弹性材料模型，屈服强度为345 MPa，弹性模量206 GPa，泊松比为0.3，网格大小取24 mm。移动荷载形式简化为6个集中荷载(间距分别为900 mm，900 mm，5 300 mm，900 mm，900 mm)，荷载移动范围32.9 m(全梁24 m+轮距8.9 m)，时间历程3.29，取值为该吊车梁94 t、A6级工作制行车最大轮压410 kN。

分析步类型采用静力通用分析步，通过ABAQUS调用Dload子程序功能，使用Fortran语言编制吊车梁上行车移动荷载子程序，模拟行车行走过程中对吊车梁施加的随时间变化位置的移动载荷，轮压荷载作用宽度取钢轨近似宽度100 mm。

2.1.2 主应力结果分析

基于移动荷载作用下的钢吊车梁有限元模型最大主应力云图，如图2所示。

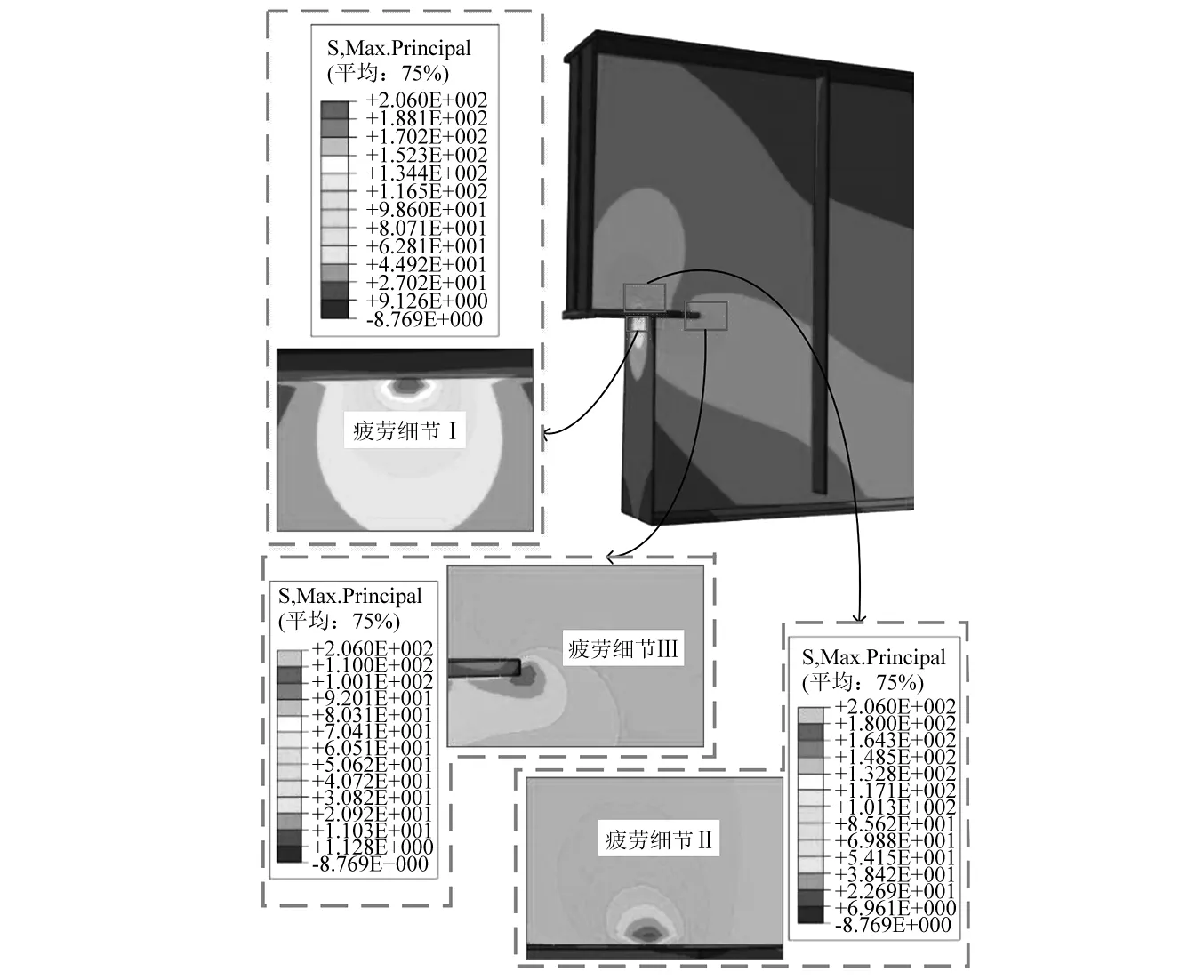
图2 危险焊接疲劳细节

吊车梁变截面部位存在3个应力集中细节，分别为危险焊接疲劳细节Ⅰ(插入板与端封板连接焊缝)、细节Ⅱ(位于端封板上方的插入板与腹板连接焊缝)和细节Ⅲ(插入板端部与腹板连接焊缝)。

由图3可知：疲劳细节Ⅰ主应力峰值最大，疲劳细节Ⅱ主应力次之，疲劳细节Ⅲ主应力最小，且行车每完整经过一次吊车梁，变截面部位受到两次循环载荷作用，是导致变截面部位破坏现象严重的原因之一。

图3 疲劳细节主应力变化规律Fig.3 Variation rule of fatigue details principal stress

2.2 裂纹扩展模拟

本文采用Franc3D与ABABQUS联合仿真进行裂纹扩展数值模拟，典型裂纹扩展分析流程如图4所示。

图4 典型裂纹扩展分析流程Fig.4 Typical crack growth analysis process

如图5所示，划分整体模型与局部模型，引入(更新)裂纹并更新裂纹前缘后，对局部模型仅保留与整体模型连接的表面网格外重新划分网格，与整体模型进行连接节点绑定组装，并计算应力强度因子，吊车梁裂纹扩展过程就是该方法的反复计算过程。

图5 吊车梁模型装配Fig.5 Crane runway girder model assembly

2.2.1 Paris公式参数

裂纹扩展速率参数根据文献[13]给出的钢材建议平均值，C=3.98×10-13，m=2.88。

2.2.2 应力强度因子

采用M-积分法计算应力强度因子，针对复合型裂纹，等效应力强度因子可以用来描述疲劳裂纹前缘应力场的强弱程度，根据文献[13]对于复合型裂纹断裂规定取值，即

(4)

式中：ΔKeff为等效应力强度因子幅值；ΔKⅠ，ΔKⅡ，ΔKⅢ分别为Ⅰ型、Ⅱ型、Ⅲ型裂纹应力强度因子幅值；v为材料泊松比；a根据文献[13]建议取1。

2.2.3 初始裂纹设置

根据2.1.2节应力分析结果，在疲劳细节Ⅰ引入初始裂纹，初始裂纹类型为表面裂纹，而任意形状的表面裂纹均可以简化为半椭圆表面裂纹进行计算，文献[14]通过蒙特卡罗仿真指出起重机焊接钢梁初始裂纹(表面长度2c)的均值和方差分别在0.25 mm和0.48 mm附近，焊接结构焊趾裂纹深度a一般假设为0.1～0.5 mm[15]。在此基础上取初始裂纹深度a=c=0.1 mm，裂纹形状比a/c=1。

2.2.4 裂纹前缘单元

沿裂纹前缘构造一圈楔形奇异单元可以解决裂纹尖端应力奇异性。如图6所示，靠近裂纹尖端内圈采用15节点奇异楔形单元，外圈采用20节点六面体单元，采用相互作用积分法计算裂纹前缘的应力强度因子，特征半径取初始裂纹尺寸10%，为0.01 mm。

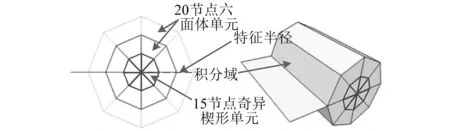
图6 裂纹尖端单元划分Fig.6 Crack tip element division

2.2.5 裂纹扩展增量

如图7所示，采用基于裂纹尺寸增量Δa的扩展方式，指定裂纹前缘中值节点的扩展增量Δam，然后根据应力强度因子幅由Paris速率公式计算节点扩展增量Δam所需荷载循环次数ΔN，再据此计算裂纹前缘其他节点扩展增量Δai，形成新裂纹前缘。使用一个曲线来对预测的新裂纹前缘的节点进行多项式拟合，即光顺化处理。目的是降低数值噪音，并将新的裂纹前缘外伸到结构表面。初始裂纹扩展增量取初始裂纹尺寸20%，即0.02 mm。

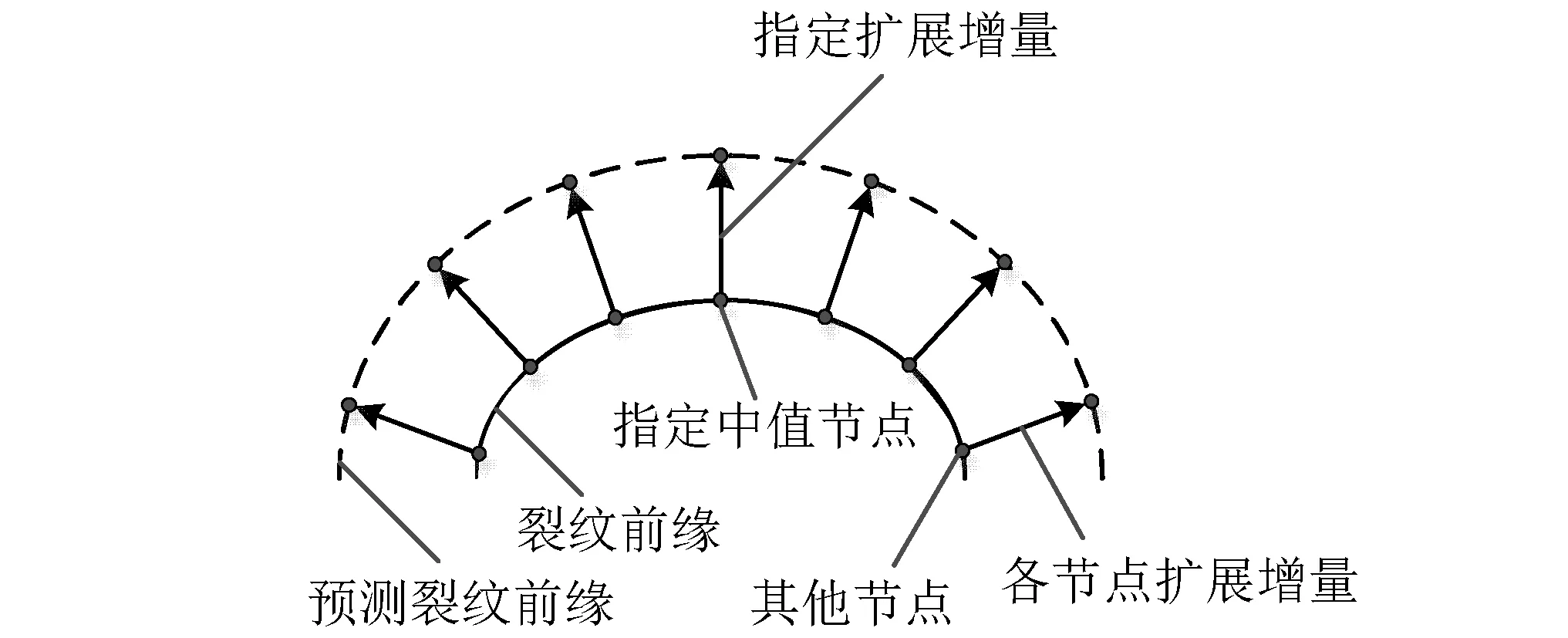
图7 裂纹扩展增量Fig.7 Crack growth increment

2.2.6 裂纹扩展终止条件

对疲劳裂纹扩展进行数值模拟时，需要进行循环计算，因此需要设定数值计算的终止条件。当数值模拟满足终止条件时，结束循环计算并输出最终的计算寿命。对于裂纹扩展数值模拟，常采用以下两种情况作为计算终止条件：

(1)裂纹前缘应力强度因子达到材料的断裂韧度(Kmax≥KC)；

(2)裂纹尺寸达到临界裂纹尺寸(a≥ac)，可根据工程实际情况指定临界裂纹尺寸。

本文依第二种情况取表面裂纹长度达到80 mm时作为终止条件，偏于安全的认为此时结构已经达到工程安全允许限值，结构发生破坏。

2.3 模型验证

为了验证文中吊车梁裂纹扩展数值模拟的可行性与合理性，进行试验对比验证，采用文献[16]的1/4缩尺直角突变式吊车梁疲劳试验数据与本文数值模拟结果进行对比，如图8所示。根据有限元应力分析结果，该区域的最大主应力方向水平夹角为10°～30°左右，与模拟裂纹扩展角度近似，而试验值则完全沿焊趾水平扩展，是由于焊接时的热影响区、残余应力和应力集中等因素使得该焊趾路径上的材料抗疲劳性能变差，应力集中程度变高，导致裂纹扩展角度与试验值有所偏差。

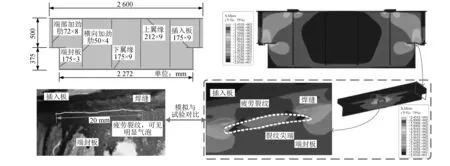
图8 裂纹扩展路径对比Fig.8 Crack growth path comparison

试件GL1(2)共进行了31次循环计算，最终达到计算终止条件的裂纹扩展寿命为86.7万次。试件GL3(4)最终达到计算终止条件的裂纹扩展寿命为51.3万次。试件GL5(6)最终达到计算终止条件的裂纹扩展寿命为32.9万次。表1给出了这3个荷载工况下试件裂纹扩展寿命的试验结果(Ntest)与有限元计算结果(NFE)的对比情况。由表可见，两者比值(Ntest/NFE)的平均值为1.05，变异系数(CV)0.34。考虑到疲劳试验存在较大的离散性，验证了本文预测疲劳寿命方法与试验结果具有较好的一致性，其疲劳计算精度已达到工程应用要求。

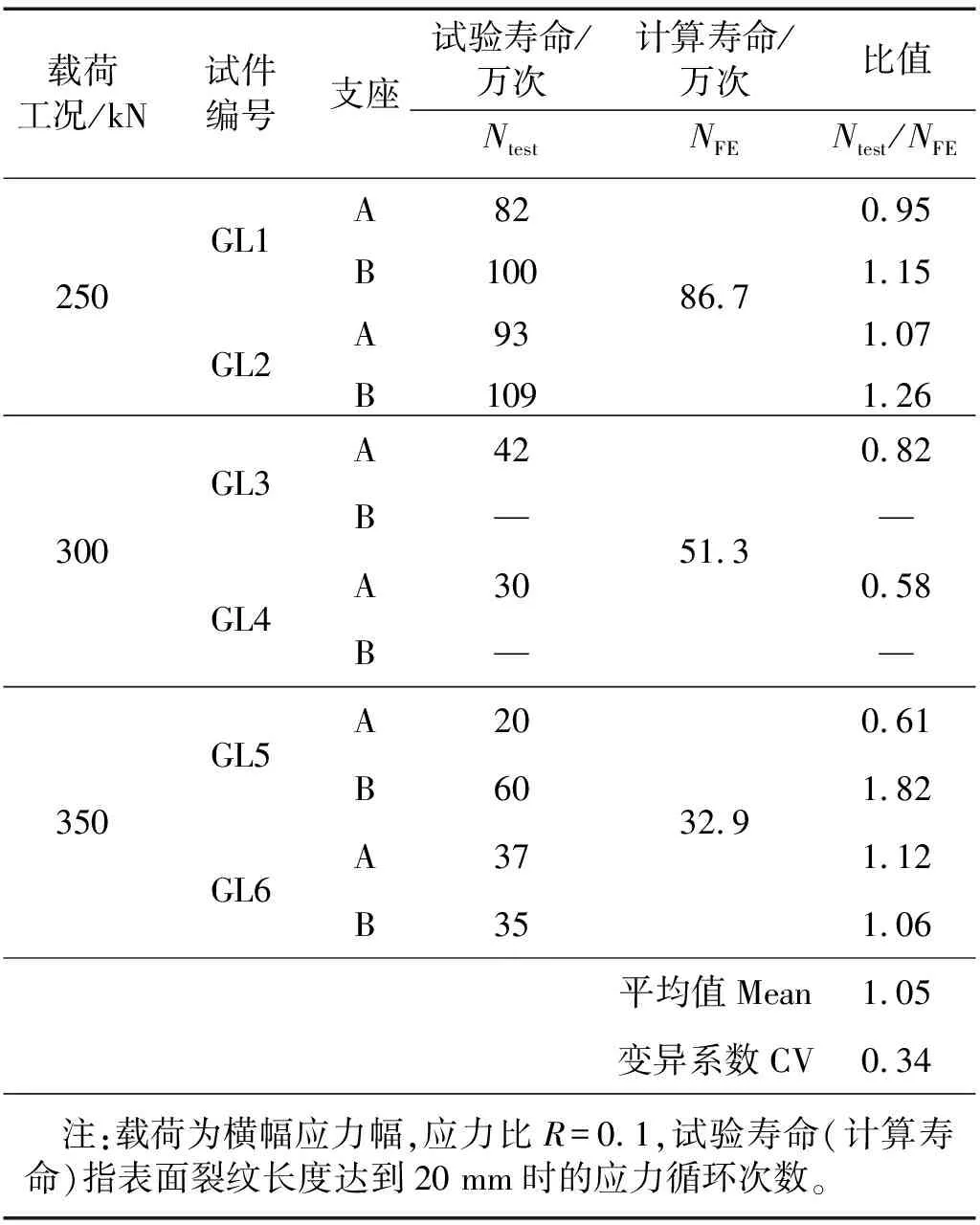
表1 试验结果(Ntest)与有限元计算结果(NFE)对比

3 吊车梁变截面参数分析

直角突变式吊车梁在变截面部位由于应力集中易产生疲劳裂纹，进而发生疲劳破坏，图9给出了吊车梁变截面示意图，可通过对变截面参数进行优化设计来降低应力集中的大小，以提高吊车梁的疲劳性能。本节研究变截面处各疲劳细节的主应力及裂纹扩展特性及寿命随支座处截面高度h2(A组)，端部加劲肋距变截面距离a(B组)，下翼缘连接长度b(C组)，端封板厚度t1(D组)和插入板厚度t2(E组)变化的影响规律，共设计以下5组参数累计33个变截面计算模型进行研究分析，具体参数如表2所示。

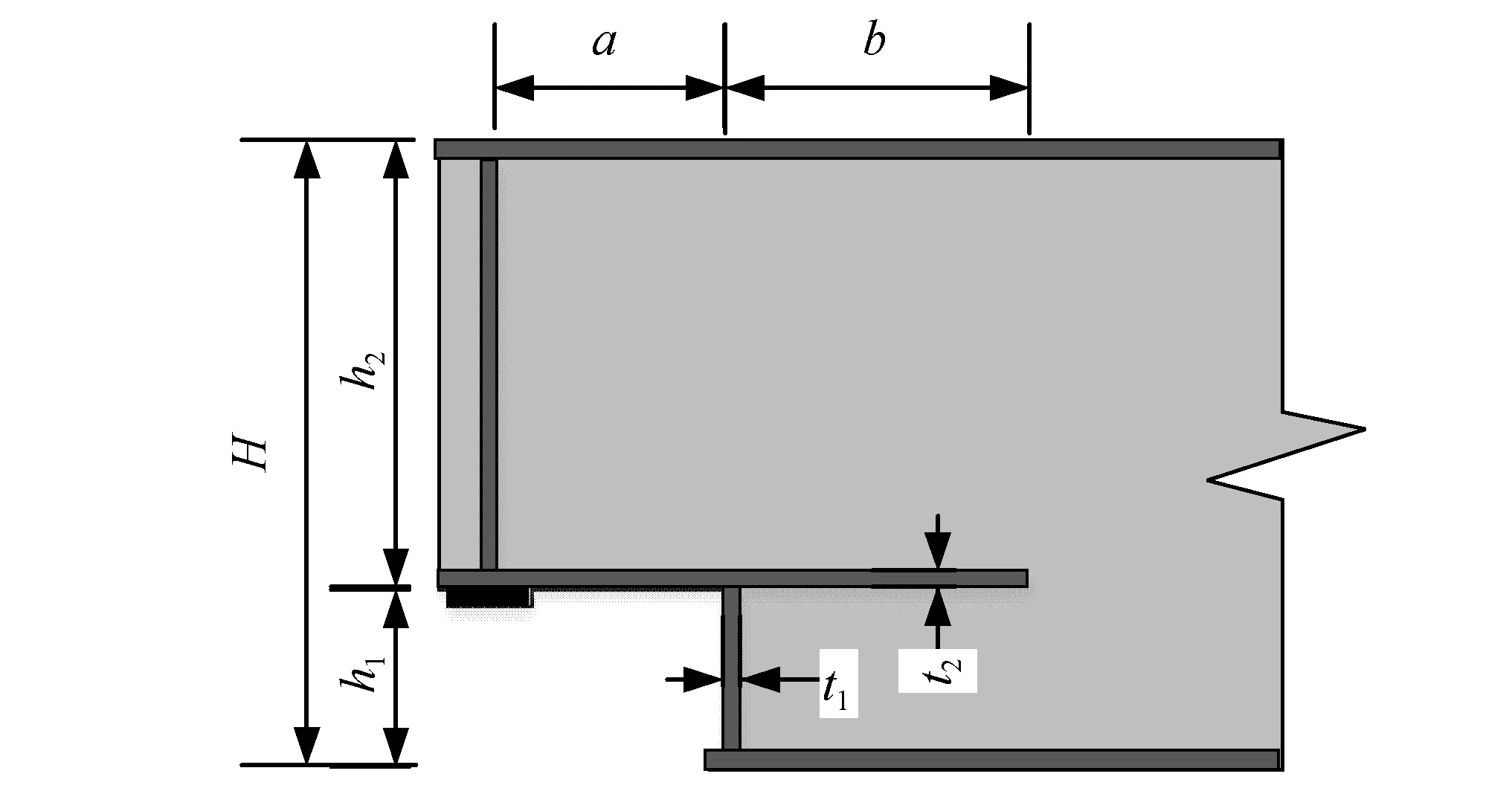
图9 吊车梁变截面示意图Fig.9 Variable section diagram of crane runway girde

3.1 变截面位置各疲劳细节主应力

图10(a)～图10(e)给出了钢吊车梁变截面位置各疲劳细节主应力随变截面参数变化的规律：

(1)由图10(a)可知：随着支座处截面高度h2的增加，疲劳细节Ⅰ、细节Ⅱ和细节Ⅲ主应力逐渐降低。h2的增加有利于减小各疲劳细节应力集中，尤其对疲劳细节Ⅰ和细节Ⅱ的主应力降低幅度最大。

(2)由图10(b)可知：随着端部加劲肋距变截面距离a的增加，疲劳细节Ⅰ、细节Ⅱ和细节Ⅲ的主应力逐渐增大。a的增加会增加各疲劳细节应力集中，其中疲劳细节Ⅲ的主应力上升速率最快，对疲劳细节Ⅲ的主应力影响程度最大；疲劳细节Ⅰ次之；疲劳细节Ⅱ主应力上升速率较小，而对疲劳细节Ⅱ主应力影响程度较小。

(3)由图10(c)可知：随着下翼缘连接长度b的增加，疲劳细节Ⅰ和疲劳细节Ⅲ主应力逐渐减小，而疲劳细节Ⅱ的主应力则在小范围内小幅下降，b的增加对疲劳细节Ⅱ影响较小，有利于减小疲劳细节Ⅰ和细节Ⅲ应力集中程度。

表2 变截面设计参数

(4)由图10(d)可知：随着端封板厚度t1的增加，疲劳细节Ⅰ的主应力逐渐降低，而疲劳细节Ⅱ的主应力逐渐上升，疲劳细节Ⅲ在较低应力水平内小范围下降。t1的增加有利于降低疲劳细节Ⅰ的应力集中，不利于疲劳细节Ⅱ，对疲劳细节Ⅲ主应力影响较小。t1的增加对于疲劳细节Ⅰ和细节Ⅱ的应力水平影响逐渐减小。

(5)由图10(e)可知：随着插入板厚度t2的增加，疲劳细节Ⅰ和疲劳细节Ⅱ主应力逐渐减小，而疲劳细节Ⅲ的主应力则基本保持不变。t2的增加有利于减小疲劳细节Ⅰ和细节Ⅱ应力集中程度，对疲劳细节Ⅲ影响较小。

图10 钢吊车梁各疲劳细节主应力变化规律Fig.10 Variation rule of principal stress in fatigue detail of steel crane runway girder

3.2 裂纹扩展分析

疲劳细节Ⅰ的主应力始终较其他两处疲劳细节大，故在疲劳细节Ⅰ引入初始裂纹进行裂纹扩展分析。

3.2.1 裂纹形状比

以A组为例，图11给出了裂纹扩展过程形状比(a/c)变化的规律：在给定的初始裂纹条件(a=0.1 mm，a/c=1.0)下，裂纹扩展初期，裂纹形状比由1.0快速下降到0.65，裂纹表面长度2c≥20 mm(裂纹沿端封板板厚方向投影深度a′>6 mm，板厚50%)后，裂纹形状比在0.6～0.65变化，裂纹形状比基本保持稳定，B～E组变化规律类似。

图11 A组a/c变化规律Fig.11 Variation rule of a/c in group A

3.2.2 应力强度因子

以A组(h2=1 250 mm)为例，图12(a)和图12(b)给出了裂纹扩展过程(A点和C点)应力强度因子幅值ΔK的变化规律。

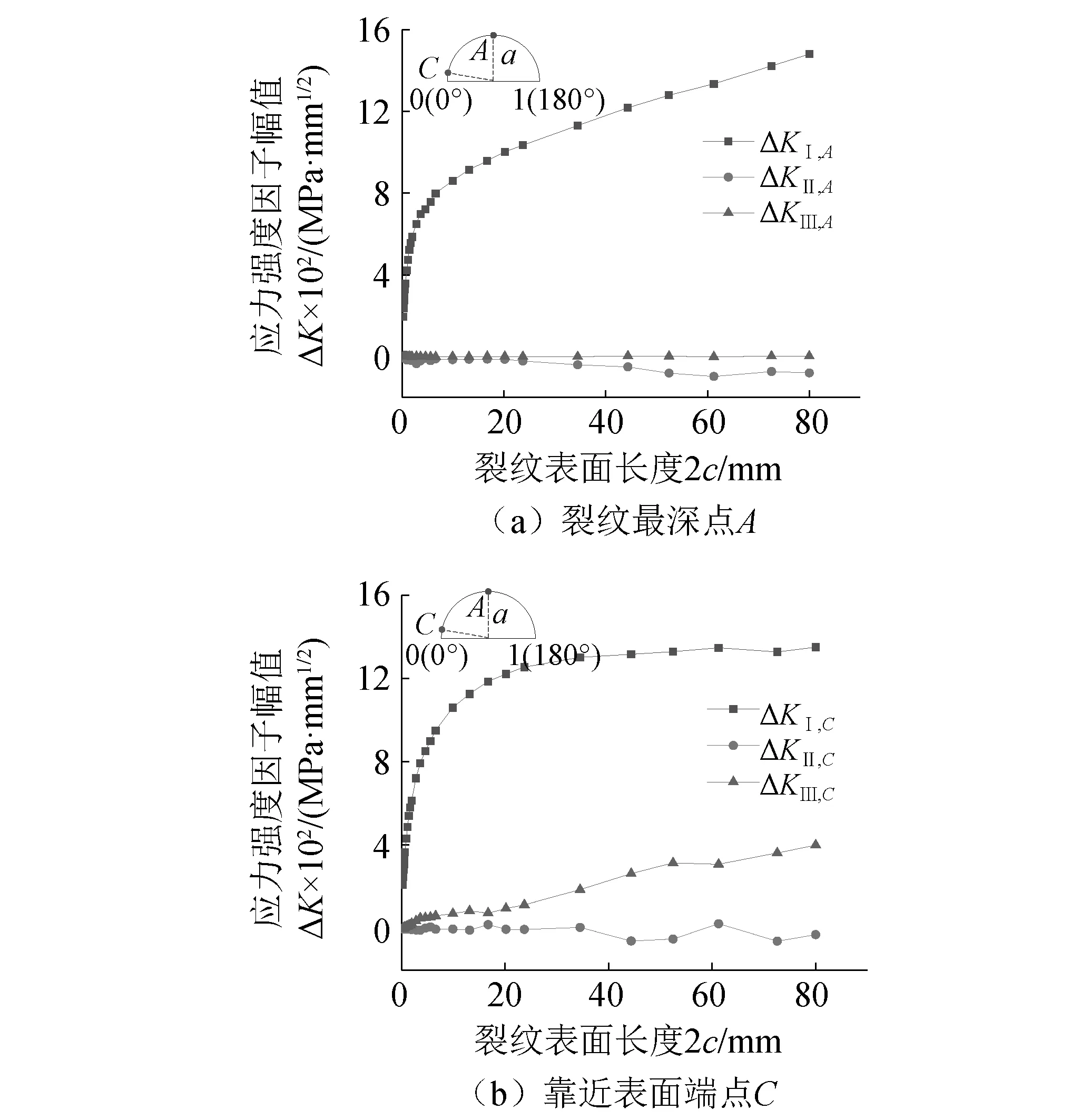
图12 A组(h2=1 250 mm)ΔK变化规律Fig.12 Variation rule of ΔK in group A (h2=1 250 mm)

由图12可知：吊车梁变截面部位疲劳破坏裂纹类型是由应力强度因子幅值ΔKⅠ控制，以张开型裂纹为主导的复合型裂纹，A(剩余)～E组变化规律类似。

以A组为例，图13(a)～图13(e)给出了裂纹扩展过程等效应力强度因子幅值ΔKeff变化的规律：随着支座处截面高度h2不断增加，ΔKeff逐渐下降，裂纹扩展初始阶段，裂纹前缘靠近表面端点(C点)的ΔKeff, C略大于裂纹前缘最深点(A点)的ΔKeff, A；在疲劳裂纹扩展前期(即裂纹表面长度扩展至8 mm左右)，裂纹靠近表面端点(C点)的上升速率大于裂纹最深点(A点)，两者均迅速上升，随后两者虽仍保持上升趋势，但增量速率均明显逐渐趋缓，当裂纹表面长度扩展至40 mm时，靠近表面端点(C点)的ΔKeff, C停止上升趋势，直至达到设定的裂纹扩展终止条件时，ΔKeff, C基本保持不变，而裂纹最深点(A点)的ΔKeff, A则呈现持续上升趋势，在裂纹表面长度扩展至60 mm左右时，裂纹最深点(A点)的ΔKeff, A已经超过裂纹靠近表面端点(C点)；ΔKeff, A不断保持增长，而ΔKeff, C没有持续上升，是由于焊趾几何突变导致应力集中，存在较大的应力梯度，裂纹靠近表面端点(C点)在裂纹扩展过程中，远离应力梯度较大的应力集中区域，B～E组变化规律类似。

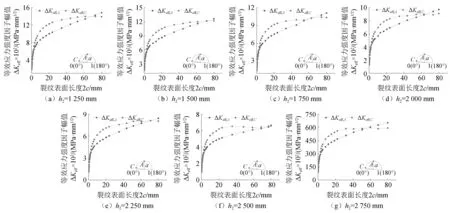
图13 A组ΔKeff变化规律Fig.13 Variation rule of ΔKeff in group A

3.2.3 裂纹扩展速率

图14(a)～图14(e)给出了钢吊车梁各疲劳细节裂纹扩展速率随变截面参数变化的规律：在裂纹扩展初期，表面裂纹长度小于8 mm时，裂纹扩展速率较低，占裂纹扩展寿命中比重较大，在此之后，裂纹扩展速率显著增加并维持速率基本不变，并未进入断裂阶段，这是由于裂纹内部沿着与端封板夹角约45°方向向插入板发展，并未直接导致端封板裂透。

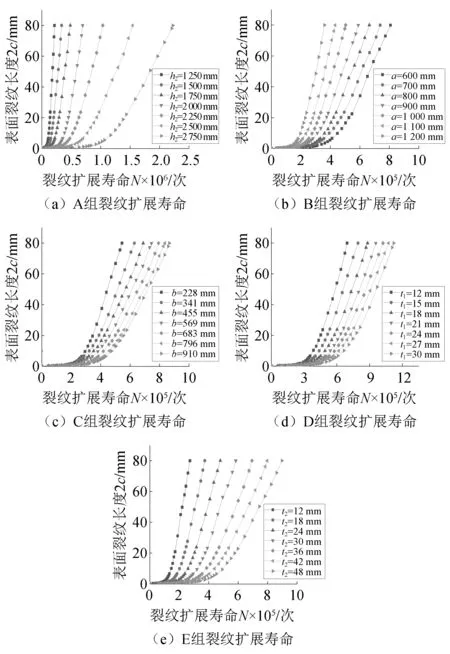
图14 裂纹扩展寿命变化规律Fig.14 Variation rule of crack growth life

3.3 裂纹扩展寿命

表3给出了参数模型的裂扩展寿命及变化率，由计算结果可知：

(1)随着支座处截面高度的增加，裂纹扩展寿命显著增加，寿命变化率基本维持不变。从裂纹扩展寿命绝对值角度观察，可以发现，支座处截面高度h2越大，裂纹扩展寿命增加越多，GB 50017—2017《钢结构设计标准》[17]建议h2/H的比值不宜小于2/3，此时支座处截面高度约为2 250 mm(h2/H=0.64)，寿命已经超过100万次，疲劳性能相对较佳。

(2)随着端部加劲肋距变截面距离的增加，裂纹扩展寿命显著减少，寿命变化率逐渐上升，钢规建议a/h2的比值宜小于0.5，此时a=1 000 mm，寿命变化率达到14%，变化率较大，建议寿命变化率(a变化100 mm)为10%以下时较合适，端部加劲肋距变截面距离a不宜大于700 mm，即a/h2≤0.35。

(3)随着下翼缘连接长度的增加，裂纹扩展寿命逐渐增加，寿命变化率逐渐减小，钢规建议b/a的比值宜大于1.5，此时b=683 mm，寿命变化率6.3%，在b/a=1时，寿命变化率(b变化0.5a)已小于10%，但b的增加对变截面构造形式无影响，仅少量增加用钢量，故可进一步增加b；当b由796 mm增加至910 mm时，寿命变化率小于5%，认为此时再增加b对疲劳强度已经没有影响，经综合考虑取值范围宜为1.5≤b/a≤2。

(4)随着端封板厚度的增加，有利于增加钢吊车梁的裂纹扩展寿命，寿命变化率逐渐减小，当t1由18 mm增加至21 mm时，寿命变化率(t1变化3 mm)为8.5%，当t1由24 mm增加至27 mm时，寿命变化率为5%，再增加t1对疲劳强度已经基本没有影响，并会导致疲劳细节Ⅱ主应力上升，降低该细节疲劳强度，经综合考虑，端封板厚度取值范围宜在18～24 mm。

(5)随着插入板厚度的增加，有利于增加钢吊车梁的裂纹扩展寿命，从寿命绝对值角度观察，随着t2的增大，寿命线性增加，t2由30 mm增加至36 mm时，寿命变化率(t2变化6 mm)18.7%；板厚增加会造成焊缝连接处存在更多缺陷，疲劳裂纹扩展速率也在加大，断裂参数C和m会有所不同[18]。本文进行裂纹扩展模拟时采用的断裂参数C和m为定值，即未考虑材料本身抗疲劳性能的降低，根据钢规进行板厚应力修正，发现在板厚超过24 mm后，考虑板厚修正后的应力已没有明显降低，t2宜取24 mm和满足设计承载力要求中的较大值，即t2=max(24 mm，设计承载力要求)。

3.4 主应力与裂纹扩展寿命规律

图15给出了参数模型(A～E组)主应力与裂纹扩展寿命的关系，可知疲劳细节Ⅰ主应力与寿命存在一一对应规律。

采用最小二乘法对参数模型(A～E组)主应力与裂纹扩展寿命进行双对数线性回归拟合，如图16所示，以lgN为因变量、lgσ为自变量，得到

lgN=-2.929 lgσ+12.615

(5)

相关系数

R=0.99

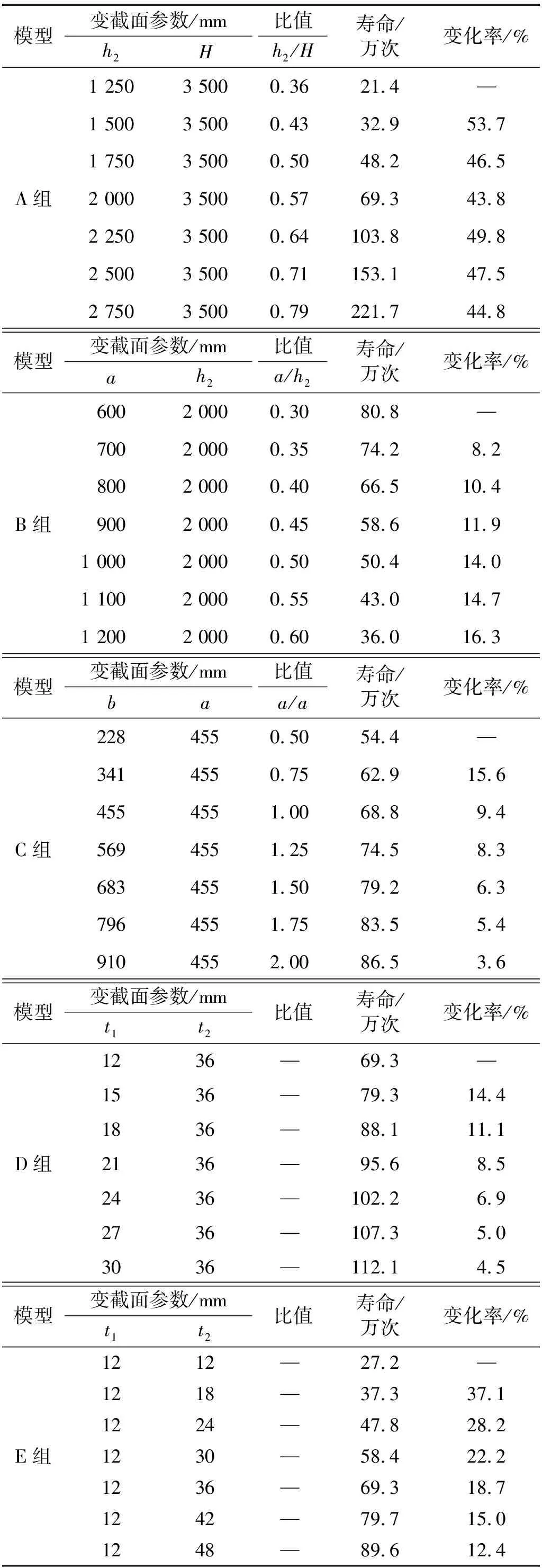
表3 参数模型(A～E组)寿命及变化率

式中：N为裂纹扩展寿命；σ为主应力。

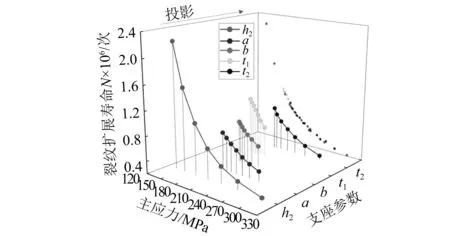
图15 主应力-裂纹扩展寿命Fig.15 Principal stress-crack growth life

图16 主应力-裂纹扩展寿命双对数线性拟合Fig.16 Logarithmic linear fitting of principal stress and crack propagation life

4 结 论

本文以线弹性断裂力学为基础，进行三维裂纹扩展数值模拟预测裂纹扩展寿命，由给定的初始裂纹，验证该方法的可行性与合理性，并对主要参数进行了数值分析，可得到以下结论：

(1)确定了直角突变式钢吊车梁主要参数对疲劳强度的影响规律：h2的增加，可有效降低各疲劳细节的应力集中；a的减少和b的增加，能缓解疲劳细节Ⅰ和细节Ⅲ的应力集中；t1的增加，可以降低疲劳细节Ⅰ的应力集中；增加插入板厚度t2能降低疲劳细节Ⅰ和细节Ⅱ的应力集中；h2，b，t1，t2与吊车梁疲劳强度正相关，a与疲劳强度负相关。

(2)吊车梁变截面部位疲劳破坏裂纹类型是以张开型裂纹为主导的复合型裂纹；当裂纹沿端封板板厚方向投影深度大于板厚50%后，裂纹形状比基本稳定0.6～0.65内；裂纹扩展后期ΔKeff, A仍呈现上升趋势，C点由于远离应力集中区域，ΔKeff, C趋于平缓。

(3)通过裂纹扩展寿命变化规律得到本吊车梁变截面参数的较合理区间为h2/H≥0.64，a/h2≤0.35，1.5≤b/a≤2，18 mm≤t1≤24 mm，t2=max(24 mm，设计承载力要求)；规范对a/h2≤0.5的规定稍微宽泛，为减少支座破坏的可能性，建议对a/h2取值做进一步限定。

(4)不同变截面参数下吊车梁的疲劳破坏，由于破坏位置具有相同连接形式的焊接细节，主应力与裂纹扩展寿命具有较好的相关性规律。