信息冲击下的金融市场尾部相依结构与风险溢出效应——以股票市场和基金市场为例

潘德春 曾建新

（1.南华大学，湖南 衡阳 421001；2.中国人民银行榕江县支行，贵州 榕江 557200）

一、引言

股票和基金是重要的资本产品，作为投资者进行投融资的重要渠道，从整体上研究股票市场和基金市场的风险问题能够为投资者选取资产组合策略和进行风险对冲提供基本思路。两个市场之间存在较强的联动性，当股票价格异常波动时，基金价格也会受到冲击和影响。同时，两个市场也具有一定的替代性，当投资者对股票市场的风险预期增加时，则会加大对基金市场的投资。受金融市场、宏观经济和国际冲击等方面的影响，在不同市场信息维度下股票市场和基金市场的价格波动带来的风险问题值得社会各界关注。因此，《中共中央关于制定国民经济和社会发展第十四个五年规划和二〇三五年远景目标的建议》明确指出，要维护金融安全，守住不发生系统性风险底线，确保国家经济安全。总之，厘清股票市场与基金市场之间的相依结构，并准确测度两者之间的风险溢出效应，既可以为投资决策提供基本启示，也可以为金融监管提供参考依据，对于维护金融稳定和促进金融改革开放具有重要意义。

二、文献综述

金融市场间的风险主要包括自身风险、组合风险、风险相依和风险溢出等，本文主要从风险传染的角度来探讨金融市场间的风险相依和风险溢出问题。

（一）风险相依研究

对于风险相依，国内外学者主要的研究模型包括格兰杰因果检验、DCC-GARCH、复杂网络和Copula等。其中，格兰杰因果检验侧重描述金融市场之间的格兰杰因果关系，如Peng et al.（2020）主要使用非线性格兰杰因果检验研究中国股票市场和国际原油市场的关系，结果表明两者之间存在双向非线性因果关系，并呈现逐渐增加的趋势。DCC-GARCH模型侧重刻画金融市场之间的动态条件相关性，如游士兵和吴雨濛（2020）通过VAR 模型和DCC-GARCH 模型分析我国股市和英国股市之间的联动性，结果表明两者之间存在长期稳定的特征。复杂网络模型侧重捕捉金融市场之间非线性和集聚性等风险特征，如刘超和郭亚东（2020）构建包含不同传染阶段的加权有向网络模型来研究主要国家股票市场之间的联动关系，结果表明在次贷危机和欧债危机中的联动关系较为显著。Copula 模型侧重刻画金融市场之间非线性和厚尾性等风险特征，如龚玉婷等（2016）使用Copula模型研究股票市场和债券市场之间的相关性，结果表明在短期内两者具有负向相依关系，而长期取决于宏观经济因素的变化。其中，目前国内外学者对于Copula模型进行相依结构方面的研究主要包括时变Copula、Vine Copula 和MRS Copula 等，朱慧明等（2016）使用时变SJC Copula 模型来分析国际原油市场和金砖国家股票市场之间的相关性，结果表明两者之间存在显著的下尾相依关系，但其相关性强度较小。郭文伟等（2020）使用高维动态R-Vine Copula 模型来研究全球主要股票市场之间的动态相依结构，结果表明欧元区和美洲区的股票市场之间相依性较强，而亚太股票市场之间相依性较低。Luo et al.（2015）使用MRS Copula模型研究主要股票市场之间的风险相依结构，主要考虑非对称相依结构和区制转换过程。

（二）风险溢出研究

对于风险溢出，国内外学者主要的研究模型集中于CoVaR、MES 和TENET 等（谢赤等，2021；王鹏飞，2020；宫晓莉等，2020；李政等，2019）。CoVaR模型侧重于研究局部的金融机构陷入危机条件下，整个金融市场的条件风险值，是目前研究系统性金融风险的主要模型（Adrian & Brunnermeier，2016；Girardi & Ergün，2013）。CoVaR 模型的估计方法主要包括分位数回归、GARCH 和Copula 等，其中，分位数回归侧重描述线性的风险溢出，如许晔（2019）使用LASSO 方法和单指标分位数回归来估计CoVaR模型，探讨我国上市金融机构对金融市场系统性风险的贡献程度，认为金融危机与股灾期间的系统性风险存在显著的上升。GARCH 模型侧重描述集聚性的风险溢出，如韩龙和吴永（2018）使用DCC-GARCH 模型来估计CoVaR 模型，研究我国金融机构对金融市场体系的风险溢出效应。Copula 模型侧重描述非线性和厚尾性的风险溢出，如赵林海和陈名智（2020）使用双时变特征的滚动窗口动态Copula模型来估计CoVaR模型，研究金融机构对金融市场系统性风险的重要性，认为证券类金融机构的风险溢出贡献程度最大。Reboredo & Ugolini（2016）使用时变Copula来估计CoVaR模型，度量主要国家原油市场和股票市场之间的极端风险溢出效应，结果表明危机爆发前后的风险溢出存在显著的差异。

综上所述，国内外学者在金融市场之间风险相依和风险溢出的度量模型方面已取得较为丰富的研究成果，但仍忽略以下问题：第一，对于研究对象而言，国内外学者聚焦于股票市场和债券市场，或者是股票市场和原油市场，或者是各个国家（地区）的股票市场，较少地研究股票市场与基金市场；第二，对于研究模型而言，国内外学者侧重于研究在市场行情下跌时金融市场之间的极端风险溢出效应，较少考虑利空消息和利好消息的综合影响。基于此，本文的创新之处如下：一方面，本文将基金市场作为重要的金融市场，基于上证综合指数和上证基金指数的日收益率数据，主要研究股票市场与基金市场的风险相依结构和风险溢出效应；另一方面，综合考虑市场行情上涨和下跌的非对称影响，构建包含利好消息和利空消息的风险相依和风险溢出模型，比较利空消息和利好消息之间的风险差异。

三、模型构建

（一）GPD模型

极端事件能够造成重大的经济损失，本文考虑极端事件的影响，使用GPD 模型来刻画股票市场与基金市场收益率序列的边际分布特征。GPD 模型属于极值理论的POT模型范畴，POT模型主要是对超过阈值的样本数据进行建模，侧重拟合尾部分布，其条件概率分布函数定义如下：

其中，X为独立同分布的随机变量，包括股票市场与基金市场收益率序列。u为阈值，y为超出阈值的样本数据。

当阈值u充分大时，Fu(y)近似服从GPD 分布。其中，GPD分布的具体定义如下：

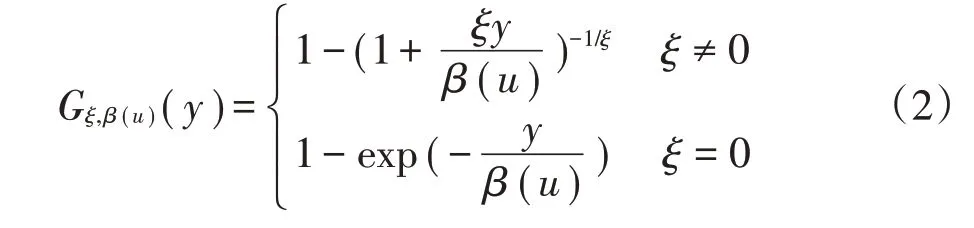
其中，ξ为形状参数，β(u)为u对应的尺度参数。

本文考虑利空消息和利好消息的影响，使用GPD模型来拟合股票市场与基金市场收益率序列的上尾和下尾，使用经验分布来拟合股票市场与基金市场收益率序列的中间样本数据。因此，股票市场与基金市场收益率序列的边际分布函数定义如下：

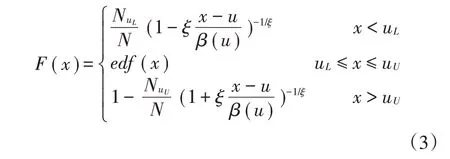
其中，uL和uU分别为下尾和上尾阈值，N为样本观测数，NuL和NuU分别为小于下尾阈值和大于上尾阈值的观测数。edf(x)为uL≤x≤uU区间的经验分布函数。

（二）时变Copula模型

时变Copula 模型能够准确地捕捉变量之间的动态性、非线性和厚尾性等相依性特征，故本文选择时变Copula 模型来刻画股票市场与基金市场之间的风险相依结构。时变Copula模型具有如下基本性质：

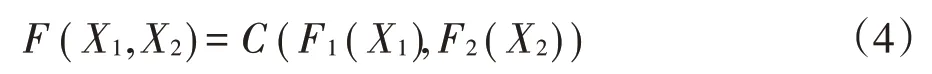
其中，F1(X1)和F2(X2)分别为股票市场收益率序列X1和基金市场收益率序列X2的边际分布函数，F(X1,X2)为F1(X1)和F2(X2)的联合分布函数，C为Copula 模型。该性质认为，若F1(X1)和F2(X2)连续，则C是唯一确定的，式（4）表明联合分布的实现问题可以分解为Copula模型和边际分布模型。

在确定Copula模型的基础上，本文使用尾部相依系数对股票市场与基金市场之间的尾部相依结构进行具体分析。限于论文篇幅，本文以时变SJC Copula模型进行相关说明，时变SJC Copula的下尾相依系数和上尾相依系数定义如下：

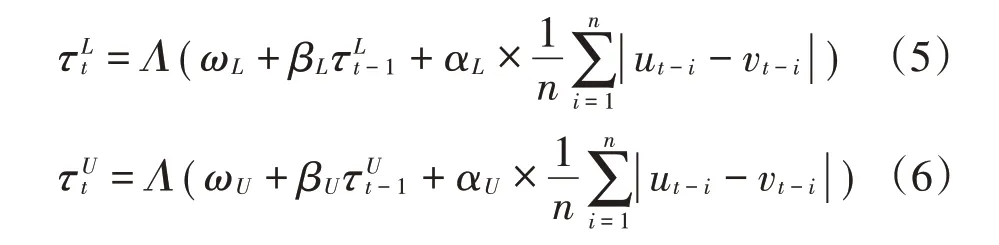
其中，ωL、βL和αL均为下尾参数，ωU、βU和αU均为上尾参数分别为下尾和上尾相依系数。

（三）时变Copula-CoVaR模型

CoVaR模型基于自下而上的角度，侧重度量单个金融机构处于风险条件下，整个金融市场体系的风险状况，属于局部影响整体的过程。相比于风险相依，风险溢出同时反映风险传染的方向和程度，包括股票市场对基金市场的风险溢出效应以及基金市场对股票市场的风险溢出效应。本文以股票市场对基金市场的风险溢出效应为例进行相关说明，根据Adrian &Brunnermeier（2016）的研究，CoVaR模型的定义如下：

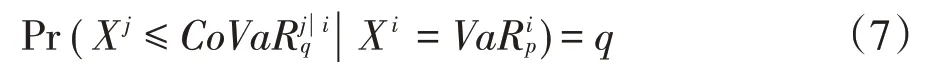
其中，Xi为股票市场的收益率序列，Xj为基金市场的收益率序列，p和q分别为VaR 模型和CoVaR 模型的分位数点。本文设置p=q=0.05 为下尾，p=q=0.95 为上尾，用于反映利空消息和利好消息的影响。因此，为股票市场在p分位数时处于风险的条件下，此时基金市场在q分位数下面临的风险价值。

考虑尾部风险的影响，本文根据Girardi & Ergün（2013）的研究，在传统CoVaR 模型的基础上，对Co⁃VaR模型的条件区域进行如下改进：

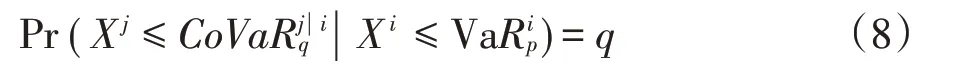
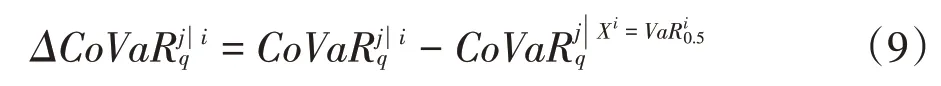
相比于分位数回归和GARCH等模型，时变Copu⁃la 模型能够较为准确地刻画股票市场对基金市场风险溢出的动态性、非线性和厚尾性等特征，故本文使用时变Copula模型来估计CoVaR模型，进而研究股票市场与基金市场之间的极端风险溢出效应。

四、实证结果与分析

（一）变量选取

本文主要研究股票市场与基金市场之间的尾部相依结构和风险溢出效应。对于股票市场而言，本文使用上证综合指数作为股票市场的代理变量，该指数能够客观地反映股票市场价格波动和收益变化的整体状况，全文使用SM表示。对于基金市场而言，本文参考何枫等（2022）的研究，选取上证基金指数来衡量基金市场，该指标属于基金价格指数，能够准确反映基金市场的综合变动情况，全文使用FM 表示。具体而言，分别根据上证综合指数和上证基金指数的日收盘价数据，可以得到股票市场与基金市场的日收益率序列，在此数据基础上进行后续的边际分布、风险相依和风险溢出分析。其中，样本的时间范围为2007年1月1日至2021年1月31日，频率为日度，样本数据为3426个，数据均来源于Wind数据库，主要使用S-Plus、R和MATLAB软件进行数据处理和建模分析。

图1为股票市场与基金市场的日收盘价序列，可以从整体上反映股票市场与基金市场的价格波动趋势。根据图1可知，股票市场与基金市场的波动趋势基本一致，反映股票市场与基金市场之间可能存在较强的相关关系，具有一定的耦合性。根据计算，股票市场与基金市场之间的Pearson 相关系数为0.9140，Spearman相关系数为0.9278，Kendall相关系数为0.7920，表明股票市场与基金市场之间存在较强的正向相关关系。另外，从动态演化的角度来看，股票市场与基金市场的日收盘价在2008年金融危机和2015年股灾期间表现出剧烈波动的特征，而在其他阶段的波动程度相对平缓，表明股票市场与基金市场的价格波动受重大极端事件的影响均较大。

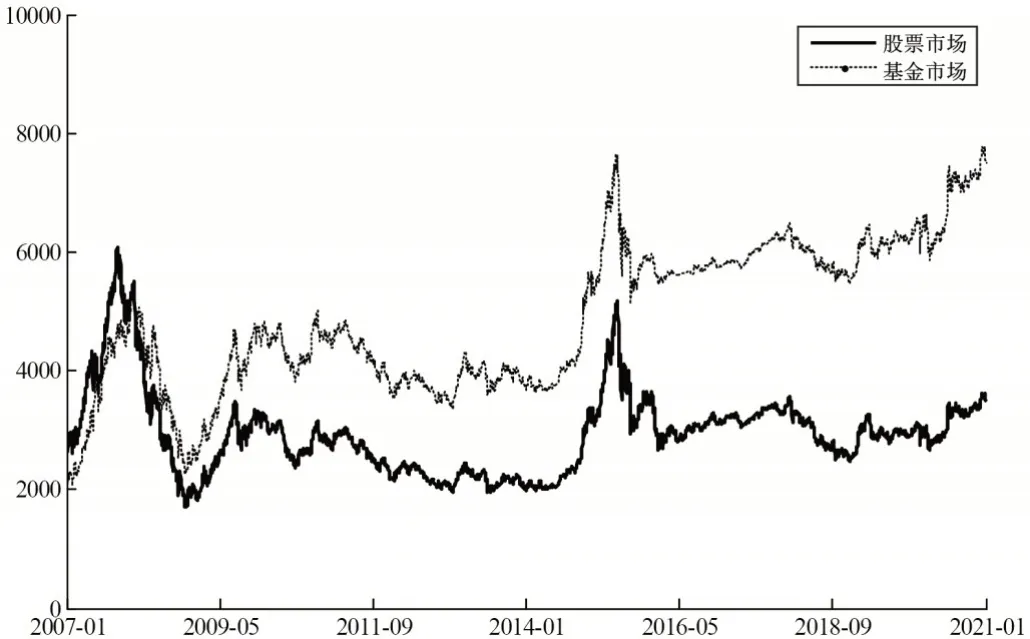
图1 股票市场与基金市场日收盘价的变化趋势

（二）边际分布分析

在进行边际分布的拟合之前，本文使用QQ 图来分别检验股票市场与基金市场收益率序列的正态性，具体结果如图2所示。

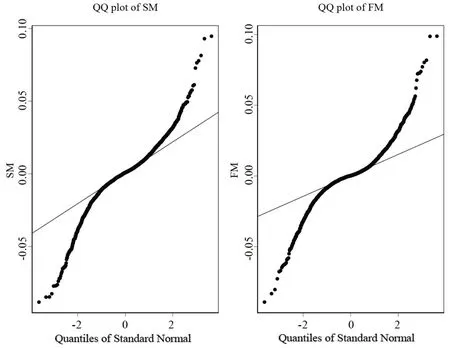
图2 股票市场与基金市场收益率序列的QQ图

根据图2可知，股票市场与基金市场收益率序列的尾部均显著偏离正态分布，表明股票市场与基金市场收益率序列均不服从正态分布，无法通过正态性检验。同时，大量的历史经验结果表明，金融时间序列具有尖峰厚尾和波动集聚等特征，不能使用传统的自回归模型进行建模分析。为了反映重大极端事件的影响，避免拟合分布的失真，本文使用GPD 模型对股票市场与基金市场收益率序列进行拟合分布，通过MLE 方法来估计GPD 模型的参数，通过Du Mouchel原则来确定GPD 模型的下尾和上尾阈值。其中，Du Mouchel原则设定超出阈值的样本观测数占样本总观测数的10%，该方法同时考虑了阈值估计的准确性和有效性，综合反映上尾阈值和下尾阈值的影响。

表1 为股票市场与基金市场收益率序列的GPD模型的参数估计结果，其中，GPD 模型的参数主要包括阈值u、形状参数ξ和尺度参数β。根据表1可知，股票市场收益率序列服从上尾参数为（0.0181，0.1077，0.0090）和下尾参数为（-0.0169，0.0195，0.0145）的GPD分布，基金市场收益率序列服从上尾参数为（0.0151，0.0891，0.0107）和下尾参数为（-0.0130，0.0513，0.0123）的GPD分布。

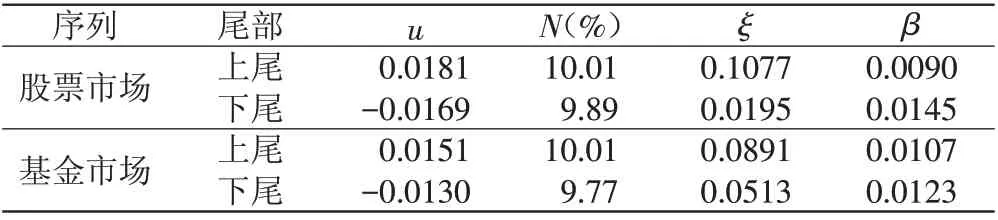
表1 GPD模型的参数估计

同时，为了检验GPD 模型的拟合效果，本文主要使用超出阈值分布进行分析，具体结果如图3 所示。根据图3可知，股票市场与基金市场收益率序列上尾和下尾的各个点均收敛于相应的曲线，表明GPD 模型的拟合效果较好，能够准确地拟合股票市场与基金市场收益率序列的边际分布。

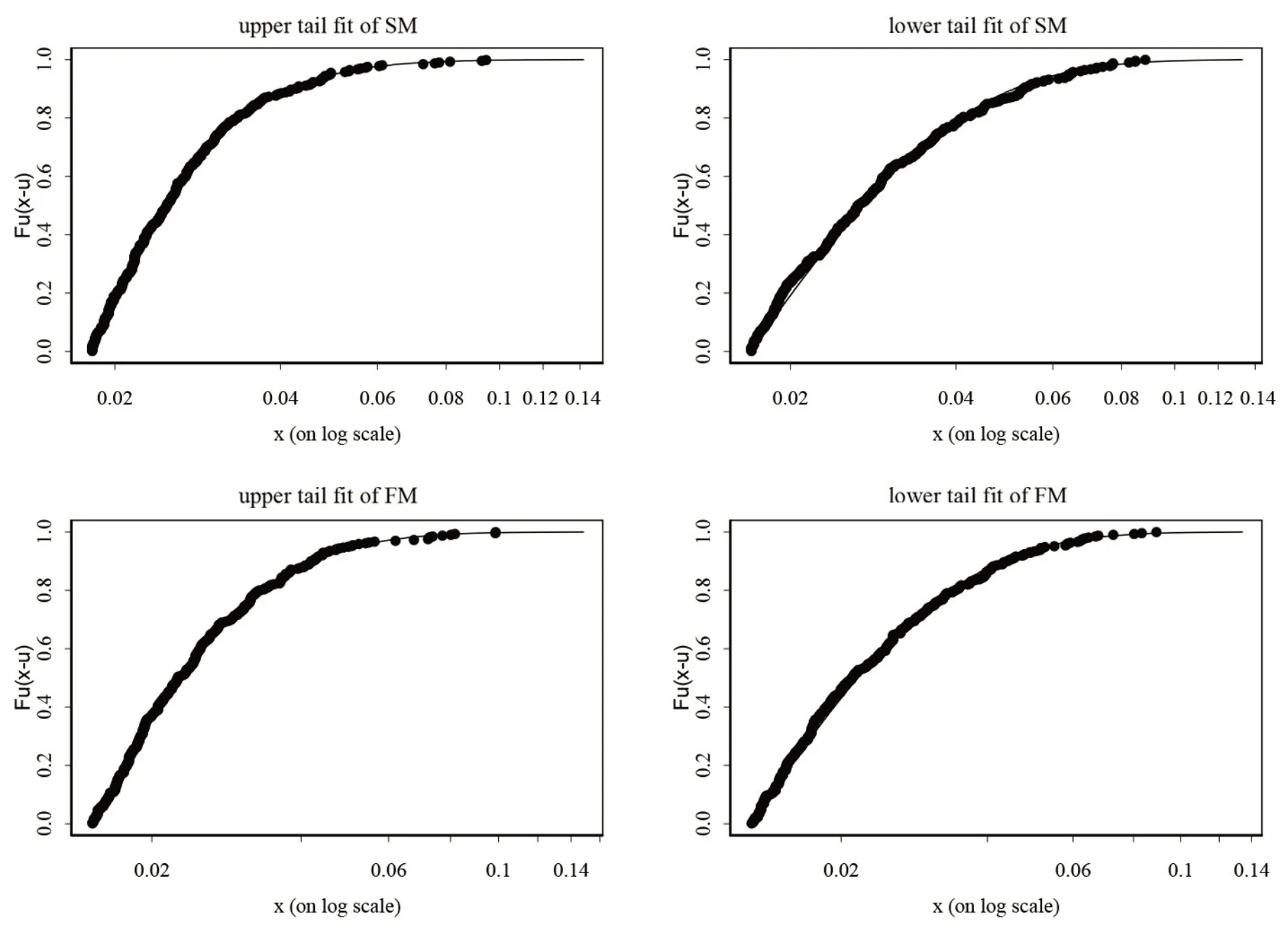
图3 超出阈值分布

（三）风险相依分析

在确定股票市场与基金市场收益率序列边际分布的基础上，本文需要确定最优时变Copula模型以及计算相应的尾部相依系数。其中，本文选取时变Nor⁃mal Copula、时变Student-t Copula、时变Gumbel Cop⁃ula、时变Clayton Copula 和时变SJC Copula 模型，这基本涵盖了时变Copula主要的风险相依特征，具有一定的代表性。具体而言，时变Normal Copula 模型具有线性的特征，时变Student-t Copula 模型具有厚尾性和对称性的特征，时变Gumbel Copula 模型仅存在上尾相依性的特征，时变Clayton Copula 模型仅存在下尾相依的特征，时变SJC Copula模型具有上尾相依和下尾相依的特征。另外，本文使用IFM方法来估计时变Copula模型的参数，该方法能够较好地处理参数过多导致估计困难的问题。

本文主要使用LogLike、AIC和BIC准则来确定最优时变Copula 模型，一般而言，若LogLike 越大，且AIC 和BIC 越小，则表明该时变Copula 模型的拟合效果越好，反之亦然。根据表2可知，结合LogLike、AIC和BIC准则，各个时变Copula模型的拟合效果按照从优到劣的排序如下：时变SJC Copula>时变Student-t Copula>时变Gumbel Copula>时变Clayton Copula>时变Normal Copula。其中，时变SJC Copula 模型的Lo⁃gLike 值最大，且AIC 和BIC 准则较小，表明时变SJC Copula 模型的拟合效果是最好的，其次是时变Stu⁃dent-t Copula 模型，最差的是时变Normal Copula 模型。因此，本文选择时变SJC Copula模型来刻画股票市场与基金市场之间的尾部相依结构。具体而言，根据时变SJC Copula模型的参数估计结果，可以计算相应的上尾和下尾相依系数，具体结果如图4所示。

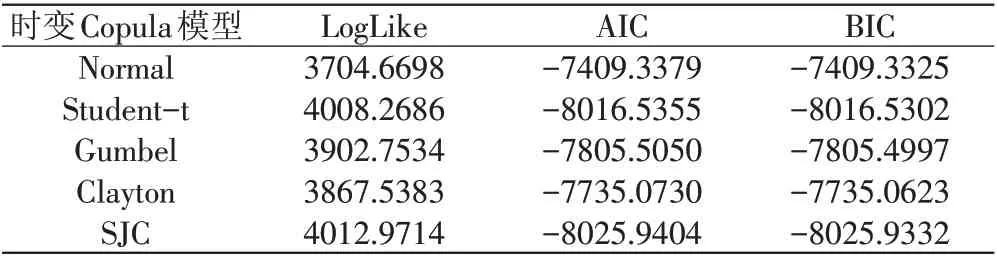
表2 Copula模型的选取

图4 股票市场与基金市场之间的尾部相依系数

图4 从上至下分别为时变SJC Copula 模型的下尾和上尾相依系数，虚线分别表示SJC Copula模型的下尾和上尾相依系数，分别为0.8373和0.8080。根据图4可知，股票市场与基金市场之间的尾部相依结构存在以下特征：第一，股票市场与基金市场之间存在较强的正向尾部相关关系，较容易出现“同涨同跌”情况。根据时变SJC Copula 模型的下尾和上尾相依系数的均值，股票市场与基金市场之间下尾相依系数均值为0.8475，大于上尾相依系数的均值（0.7725），表明股票市场与基金市场之间存在下尾相依的非对称性特征，更容易受到利空消息的冲击和影响。第二，从动态演化的视角来看，股票市场与基金市场之间的上尾相依系数波动程度大于相应的下尾相依系数，表明虽然股票市场与基金市场之间的相依性受到利空消息影响的程度更大，但其相依性受到利好消息影响的波动更大。另外，股票市场与基金市场之间的尾部相依系数在2008年金融危机和2015年股灾期间均出现较大的波动，表明重大极端事件显著影响股票市场与基金市场之间的尾部相依结构。

（四）风险溢出分析

金融风险一般包括自身风险和风险溢出两个部分，其中自身风险也存在下尾风险和上尾风险。在分析股票市场与基金市场之间的尾部风险溢出效应之前，本文对股票市场与基金市场的自身风险VaR进行测度，以便为相关的风险溢出效应提供参考和依据。为了便于分析和比较，本文对股票市场与基金市场的下尾风险均取绝对值。图5 从上至下分别为股票市场与基金市场的尾部风险。首先，股票市场的风险大于基金市场的风险，具体而言，股票市场的下尾风险均值为4.0976，上尾风险均值为3.8677，而基金市场的下尾风险均值为3.6693，上尾风险均值为3.3264。其次，股票市场与基金市场的尾部风险均存在非对称性的特征，股票市场与基金市场的下尾风险均大于相应的上尾风险，受到市场行情下跌或者金融危机的影响更大。最后，从动态变化趋势来看，股票市场与基金市场的尾部风险在重大极端事件爆发前后具有显著差异，在2008 年金融危机和2015 年股灾期间的波动程度明显更大，重大极端事件期间的尾部风险处于更高的水平，而在其他时期的股票市场与基金市场尾部风险的波动较为平缓，且变化程度较小。

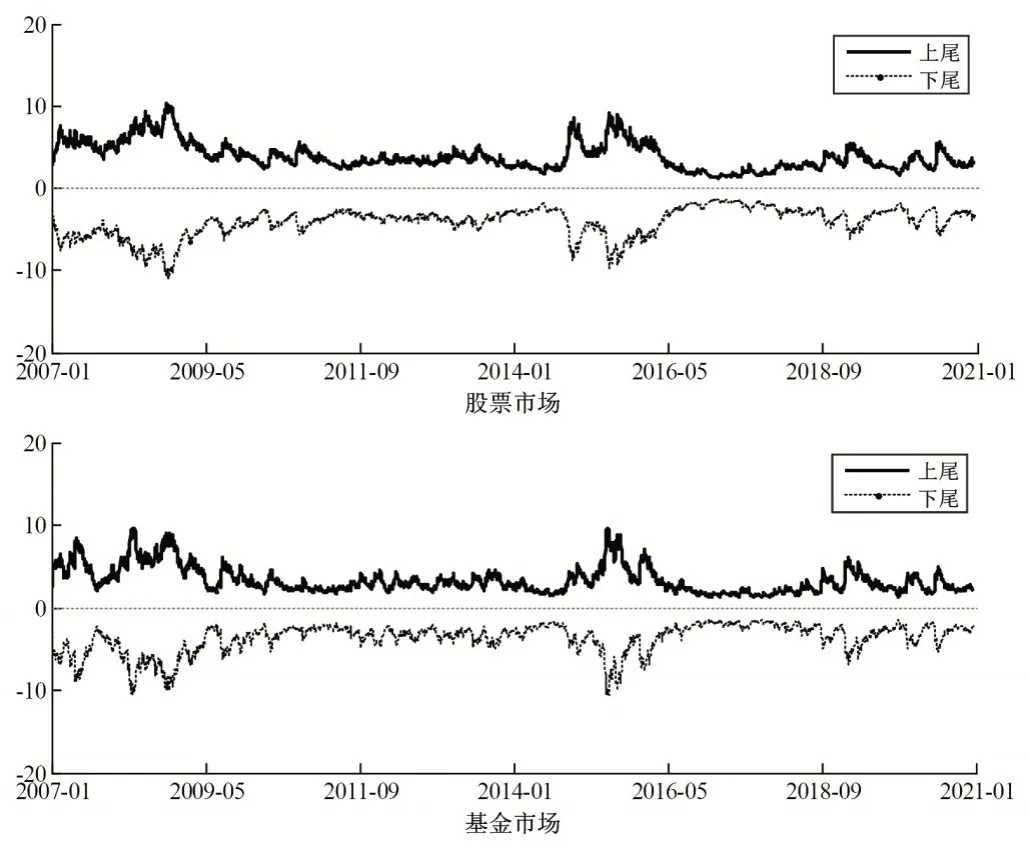
图5 股票市场与基金市场的尾部风险

本文使用时变SJC Copula 模型来估计CoVaR 模型，以此来研究股票市场对基金市场、基金市场对股票市场的尾部风险溢出效应。图6 从上至下分别为股票市场对基金市场的上尾和下尾风险溢出效应、基金市场对股票市场的上尾和下尾风险溢出效应。为了便于分析和比较，本文对相应的下尾风险溢出效应均取绝对值。根据图6可知，股票市场与基金市场之间的尾部风险溢出效应存在以下特征：第一，股票市场对基金市场的风险溢出效应、基金市场对股票市场的风险溢出效应均具有非对称性，其下尾风险溢出效应均大于上尾风险溢出效应，对利空消息的反应更为脆弱和敏感。具体而言，股票市场对基金市场的下尾风险溢出效应均值为6.8753，而股票市场对基金市场的上尾风险溢出效应均值为6.3318。另外，基金市场对股票市场的下尾风险溢出效应均值为4.1728，而基金市场对股票市场的上尾风险溢出效应均值为3.9478。因此，股票市场对基金市场的风险溢出效应大于基金市场对股票市场的风险溢出效应，其主要原因在于股票市场成交金额更大，具有规模优势，同时股票市场的价格波动更为激烈，导致股票市场对其他金融市场具有更高的风险传染能力。第二，从时序变化趋势来看，类似于股票市场与基金市场的自身风险，股票市场对基金市场的风险溢出效应、基金市场对股票市场的风险溢出效应基本一致，受到重大极端事件的影响较大。在2008年金融危机、2015年股灾、2018年以来的中美贸易摩擦以及2020年以来的新冠肺炎疫情等重大事件爆发后，股票市场与基金市场的价格均出现暴跌的情况，大量投资者遭受经济损失和风险危机，对市场前景预期持悲观态度，股票市场对基金市场的风险溢出效应、基金市场对股票市场的风险溢出效应均出现剧烈波动，其下尾和上尾风险溢出效应均呈现急剧增加的趋势。

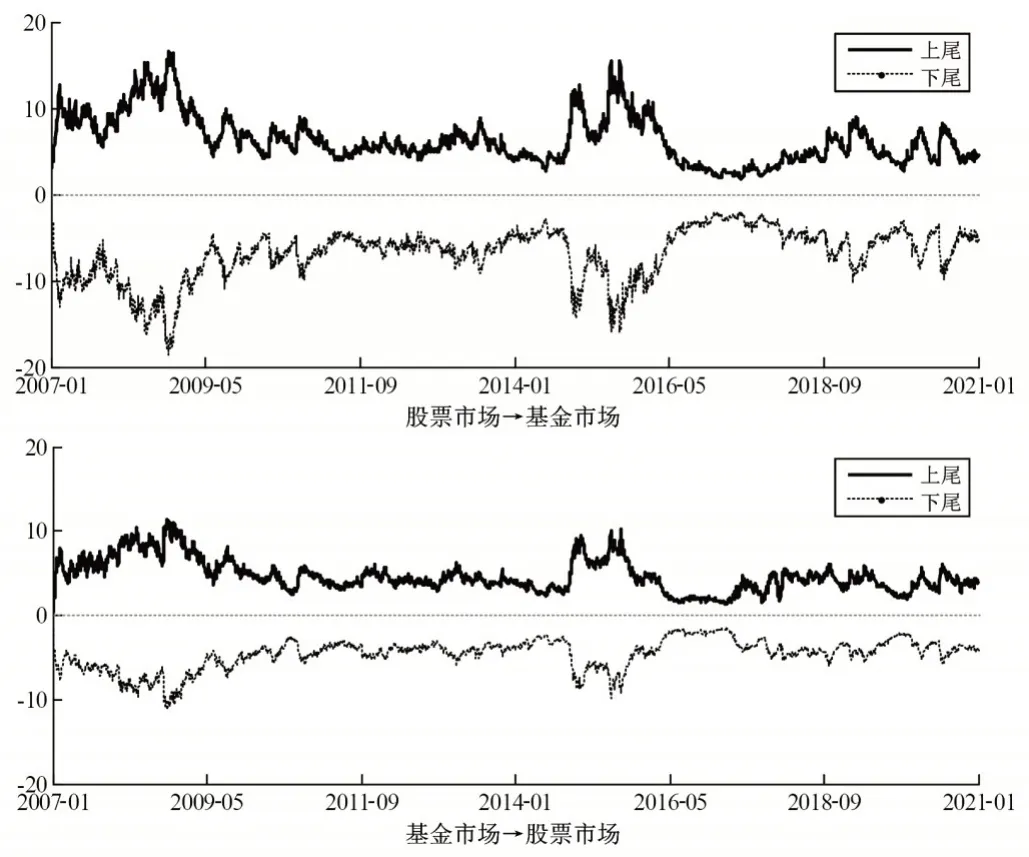
图6 股票市场与基金市场之间的尾部风险溢出效应

五、结论与建议

本文考虑利空消息和利好消息的非对称影响，使用时变SJC Copula CoVaR 模型研究股票市场与基金市场之间的尾部风险相依结构和风险溢出效应。具体而言，基于股票市场与基金市场的日收益率序列数据，使用GPD 模型来拟合股票市场与基金市场的边际分布，使用时变SJC Copula模型来刻画股票市场与基金市场之间的尾部风险相依结构，使用时变SJC Copula CoVaR 模型来度量股票市场与基金市场之间的尾部风险溢出效应。结果表明：第一，股票市场与基金市场之间存在较强的正向尾部相关关系，且具有下尾相依的非对称性和非线性特征，下尾相依性大于上尾相依性，表明股票市场与基金市场之间的风险相依受到利空消息的影响更大，对危机和损失等下跌行情较为敏感；第二，股票市场与基金市场之间尾部风险溢出效应具有时变性和非对称性特征，股票市场与基金市场之间的下尾风险溢出效应均小于股票市场与基金市场之间的上尾风险溢出效应，表明股票市场与基金市场之间的风险溢出对利空消息的反应更为敏感；第三，从动态演化的视角来看，股票市场与基金市场之间的尾部风险相依结构和风险溢出效应均受重大极端事件的影响较大，特别是2008 年金融危机和2015 年股灾的影响，重大极端事件的爆发使得其风险相依和风险溢出程度急剧增加和波动，并具有一定的持续性。基于此，本文提出的相关风险防控建议如下：

第一，完善股票市场与基金市场之间的协同监管机制。股票市场与基金市场之间存在较强的正向尾部相关关系，且具有明显和重要的风险溢出效应。因此，在“一委一行两会一局”的监管框架之下，各个监管部门应该在跨市场风险方面加强监管协同和合作，实现两个市场的信息共享、互联互通和协调联动，增强金融风险监管的责任意识，共同推进金融风险管理工作的有序、有效开展，确保金融防控的决策部署落到实处，防止两个市场出现监管真空，又要避免重复无效监管。

第二，健全重大风险应急机制。重大极端事件对股票市场和基金市场之间的风险溢出效应产生重要的影响，特别是对股票市场形成强烈的风险冲击和震荡。基于此，要从预防和控制的角度来完善股票市场和基金市场相关风险的形成、积累、传染和演化等，对股票市场和基金市场的风险联动进行科学预警，并系统制定针对股票市场和基金市场的风险监管方案，确保两个市场在重大极端事件发生重大风险前后得到及时和有效的风险处置。

第三，完善市场消息的监控和处理机制。相比于利好消息，利空消息对股票市场和基金市场的相依结构和风险溢出的反应更为强烈。基于此，一方面，对市场消息进行科学和系统的甄别，面对虚假消息和小道消息等谣言，各个部门要通过官方平台发布权威信息，防止股票市场和基金市场出现恐慌情绪和盲目投资的状况。另一方面，当利空消息出现时，相关部门要及时加以回应和应对，科学加强形势研判，出台一些针对性的利好政策和措施，防止股票市场和基金市场相关风险的扩散。