上游扰动条件下尾水管涡带演化和压力脉动研究

2022-08-05徐李辉罗竹梅

农业机械学报 2022年6期

郭涛徐李辉罗竹梅

(1.昆明理工大学建筑工程学院，昆明 650500；2.昆明理工大学能源与动力工程系，昆明 650093)

0 引言

随着经济的飞速发展，人们对电力资源的需求急剧增长，特别是分时段用电量差异明显，水力发电机组在电网中同时承担着调峰调频的任务，水力机组输出功率频繁改变，水轮机不可避免地处于偏离最优工况运行情况[1]。活动导叶按水流流动方向布置在固定导叶之后，水流经蜗壳与固定导叶后的出流角是固定不变的，水轮机通过改变活动导叶开度来调节流量及水流环量，从而达到调整水轮机输出功率的目的[2-4]。尾水管涡带是混流式水轮机在偏离最优工况运行时，尾水管中出现的一种偏心螺旋状涡旋运动；同时也是混流式水轮机在偏离最优工况运行的一种固有水力特性，是水力不稳定性的表征和结果，严重时会影响运行稳定性及造成疲劳破坏等，因此偏离最优工况下尾水管涡带和压力脉动特性研究受到大量学者持续关注[5-6]。

文献[7-8]研究了转轮出口的流场情况，文献[9]研究了无叶区内部流场变化，文献[10-11]分别从水轮机出水口旋流和动静干涉的角度分析了压力脉动特性的传播，为研究尾水管内流动分布提供了必要的依据。文献[12]提出了一种基于零环量单位流量的相对流量法和基于叶片出口压力脉动的相对幅值法来预测原型机尾水管进口压力脉动，对12个电站水轮机模型和原型机尾水管压力脉动试验结果进行比较，吻合性较好。之后诸多学者研究了不同工况下(小流量、小开度工况)，水泵水轮机[13-15]、贯流式水轮机[16]、混流式水轮机[17-20]等机型的尾水管涡带及压力脉动。文献[21-22]应用不同涡识别准则捕捉尾水管涡带，把在涡带形成过程中诱发的压力脉动信号分解为同步及非同步运动分量，并对其进行了动力学分析，进一步探究了尾水管涡带的复杂流动特征及其动力学特性。文献[23]基于熵产理论分析了水泵水轮机尾水管内的局部熵产分布情况、流动状态，探究了涡带的产生机理。尾水管中的偏心回转涡带与肘管内壁的撞击是引起机组振动的重要原因之一，文献[24]通过加长泄水锥、水力干扰、加长泄水锥与水力干扰共同作用的3种改进方案，改善了尾水管内的压力脉动。涡结构是水轮机内部非定常流动的典型结构，其存在会导致水轮机内部压力波动大、诱发机组振动及水轮机部件疲劳等。文献[25]提出了一个新的代表涡的变量Liutex向量R，并基于该变量建立了Liutex 涡识别方法，该方法得到了较为广泛的推广与应用[26-27]。该方法能更准确地辨别流场内不同尺度的涡结构，且克服了研究人员主观确定涡识别变量阈值的不足，使得流场中的涡识别更加客观且具有可比性，可以推广应用到水力机械内部涡识别的研究中。

纵观相关研究发展历程，用新型的涡识别方法显示尾水管涡带的时空演化过程的成果相对较少。本文以HLA551-LJ-43型混流式水轮机为研究对象，基于Liutex涡识别方法分析上游扰动改变对尾水管涡带和压力脉动的影响。

1 研究对象和数值方法

1.1 控制方程

水轮机内部三维不可压缩湍流流动可描述为

(1)

式中τij——剪切应力，Pa

ui、uj——速度分量，m/s

p——压力，Pat——时间

ρ——流体密度，kg/m3

Sij——附加源项，N/m3

xi、xj——笛卡尔坐标分量，m

基于雷诺时均模型中的剪切应力输运(Shear stress transport，SST)湍流模型执行湍流瞬态计算，SST 湍流模型实现了从边界层内部的k-ω模型到边界层外部的高雷诺数k-ε模型的逐渐过渡，在预测近壁面流动和捕捉旋转机械的流动分离现象等方面具有较大优势[28-30]。

1.2 Liutex涡识别方法

文献[31]提出了一种描述涡的数学定义——Liutex方法，该方法对涡进行了新的数学定义，即以R来表示Liutex值。其数学表达式为

(2)

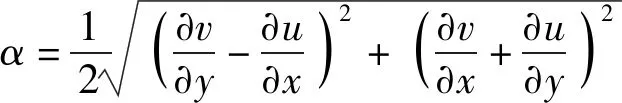
(3)

(4)

式中u、v——坐标x、y方向上的速度分量

Liutex值表示流体刚性旋转强度，且可以给出流体质点的刚体旋转轴。具有对阈值依赖性小、能够清晰合理地显示涡形态的优点。

1.3 混流式水轮机模型和边界条件

混流式水轮机型号为HLA551-LJ-43，其机组实物如图1所示，图2为所取计算域几何模型(以导叶开度48.74 mm为例)，模型包括蜗壳区域、导水区域(8个固定导叶和16个活动导叶)、转轮区域(13个叶片)和尾水管区域。该型号水轮机，设计水头10 m，设计流量0.7 m3/s，设计转速600 r/min。

图1 混流式水轮机模型实验台Fig.1 Model Francis turbine test rig

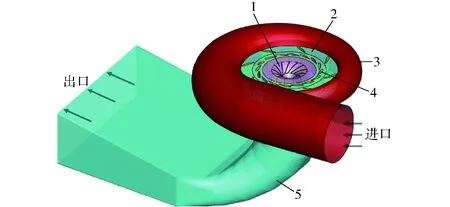
图2 混流式水轮机全流道计算域Fig.2 Whole computational domain of Francis turbine1.转轮 2.固定导叶 3.蜗壳 4.活动导叶 5.尾水管

图3 混流式水轮机全流道网格Fig.3 Grids of Francis turbine

采用滑移网格技术，在转轮区域动静交界面上设置滑移网格交接面以处理导叶与转轮、转轮与尾水管之间动静干扰流动的数据传递。计算域全流道采用六面体网格划分，如图3所示，其中转轮区域边界层网格最小达到0.05 mm，网格数量是影响数值模拟精度的关键因素之一，本文选取4种网格数对混流式水轮机在流量0.7 m3/s、转速600 r/min工况下进行三维湍流稳态计算，以效率为目标函数进行网格无关性验证，其结果如图4所示。可以看出，当网格数量达到1300万之后，随着网格数的增加，效率幅度变化很小而趋近于一个恒定数值，说明此时网格数的增加已几乎不对结果产生影响。在保证计算结果可靠性的前提下，为尽可能降低网格数以减少计算耗时，选择模型网格总数为1 306.782 8万，网格节点数为1 263.297 0万。整个转轮区域的所有叶片迎水面和背水面的y+平均值云图和时域图，如图5所示。可以看出y+满足SST湍流模型的计算精度要求。

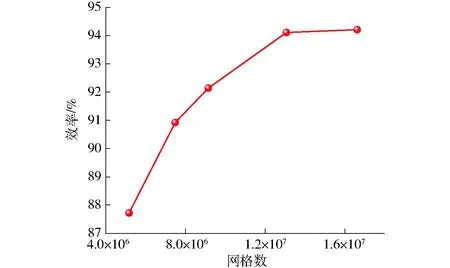
图4 网格无关性验证结果Fig.4 Results of grid independency test

图5 叶片表面y+值Fig.5 y+ value on runner blades

蜗壳进口处为速度进口Dirichlet边界条件，尾水管出口处为自由出流，壁面为无滑移边界条件。依据图6综合特性曲线及相似准则，考虑了包含小开度(偏离最优工况)和最优工况的αM=13.50 mm(攻角8°)、αM=26.17 mm(攻角16°)、αM=38.05 mm(攻角24°)、αM=48.74 mm(攻角32°，最优工况)4种导叶开度情况(导叶开度示意图如图7所示)，图中n11M、Q11M分别为A551-35模型水轮机的单位转速、单位流量。控制方程在空间上采用有限体积法进行离散，时间上采用二阶全隐式格式。扩散项和压力项采用二阶中心格式，对流项采用二阶迎风格式。转轮旋转周期T为0.1 s，计算时间步长取0.001 s，每个时间步长对应转轮旋转1%，保证了求解精度。计算了22个旋转周期，通过检测所设置监控点变量(速度、压力等)的周期性和方程的最大残差小于10-5，来判断收敛性，取流场稳定后的最后两个旋转周期进行结果分析，纯计算时间约60 d。

图6 A551-35模型水轮机综合特性曲线Fig.6 Model comprehensive characteristic curves of Francis turbine

图7 导叶开度示意图Fig.7 Opening of guide vane

2 结果分析

混流式水轮机转轮是基于一定流量设计的，在这个流量下，转轮叶片相对出流角是固定的，转轮圆周方向的绝对速度分量很小，尾水管内异常流动现象发生区域较小。如图8所示，水流质点随转轮叶片运动的相对速度为W，水流质点随转轮旋转的牵连速度为U，水流质点对定系的绝对速度为V。随着导叶开度改变，上游扰动不断变化，流量和转轮进口冲角发生改变，引起转轮出口绝对流动角β大小、方向发生变化，产生与转轮旋转方向相同或者相反大小不一的绝对速度圆周分量VU，导致在尾水管直锥和弯肘段观察到不同形状的涡带。尾水管涡带是尾水管内死水区中的一种拧旋流，涡带的旋转、失稳会导致尾水管振动剧烈，其产生的基本条件是转轮出口处流体存在圆周方向的速度分量。

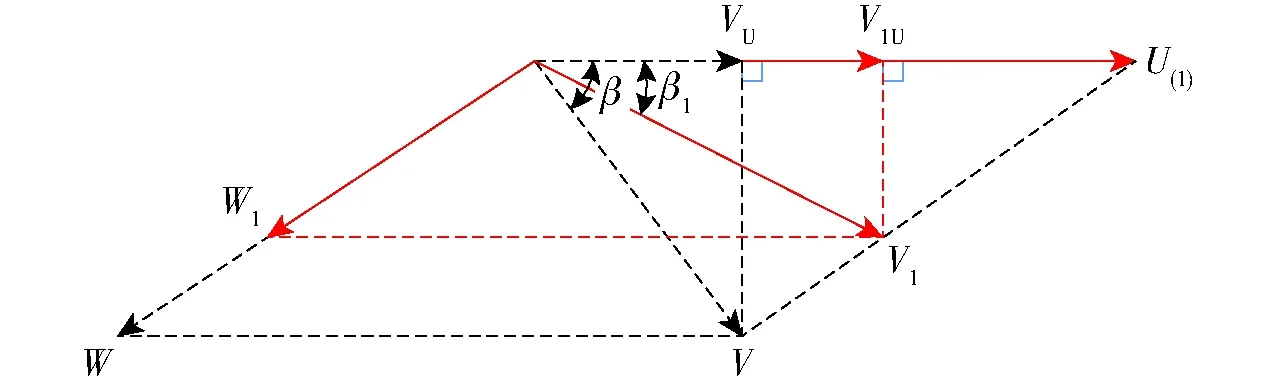
图8 转轮叶片出口速度三角形Fig.8 Velocity triangles at leading edge of runner blade

2.1 αM=48.74 mm(最优工况)时尾水管流型分析

图9为最优工况下运行时，基于Liutex方法捕捉到的一个周期内的尾水管涡带形状的可视化展示。从图中可看出，该工况下尾水管涡带可分为A、B、C 3部分，分别为转轮出口处的稳定旋流结构，与文献[32]实验对应较好、肘管段内的螺旋形部分和下游的杂涡部分。从尾水管涡带的时程变化可看出，处于锥管段内的第1部分稳定旋流结构A为纺锤形涡带，具有较好的轴对称性和稳定性，大小不随时间变化而变化。而第2部分螺旋形涡带B，稳定性稍差，随着时间的迁移一直在作与转轮旋转方向相反的偏心螺旋增减运动，破碎后形成第3部分杂涡C分布于弯肘段下游。

图10为尾水管一个周期内的流线图，在最优工况下尾水管直锥段和弯肘段流线平稳顺畅，特别是锥管段，流速从中间向管壁呈对称性，且流态稳定。只是由于涡带对水流的排挤作用，造成涡带与壁面之间出现明显的高速区；在尾水管肘管段内螺旋形涡带位置处，流态较紊乱，随着时间的变化，可以看到流线出现延长、密集甚至出现微小回流；说明水轮机在最优工况下运行时，尾水管上游转轮出口处流体流态较好，涡带比较细小，强度低，涡带尾部的旋转没有直接冲击肘管段内壁，不会引起强烈的噪声和压力脉动，水力损失小，不足以诱发对机组运行造成威胁的压力脉动。图11为该工况下尾水管内的瞬时湍动能图。从图中也可看出，在最优工况下，尾水管近壁区域湍动能几乎为零，而尾水管涡带区域湍动能均在0.8 m2/s2以上，说明涡带对流场影响较大，湍动较剧烈，是引起能量损失的原因之一。

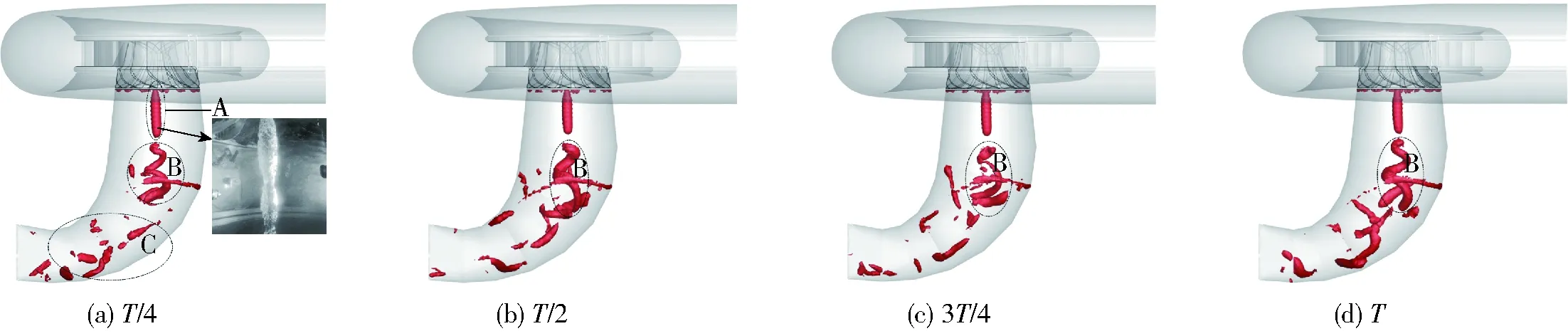
图9 αM=48.74 mm(最优工况)时尾水管涡带(Liutex值50)Fig.9 Vortex rope in draft tube under the best efficiency point (Liutex value is 50)

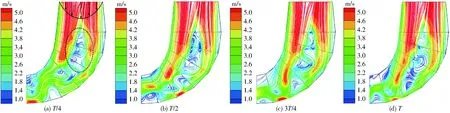
图10 αM=48.74 mm(最优工况)时尾水管子午面速度流线Fig.10 Velocity streamlines in draft tube under the best efficiency point

图11 αM=48.74 mm(最优工况)时尾水管子午面湍动能Fig.11 Turbulent kinetic energy in draft tube under the best efficiency point

2.2 偏离最优开度时尾水管流态分析

图12～16为偏离最优工况运行时一个周期内的尾水管涡带形状以及流线、湍动能的可视化展示，与文献[32]中实验所得尾水管涡带形状相互对应。

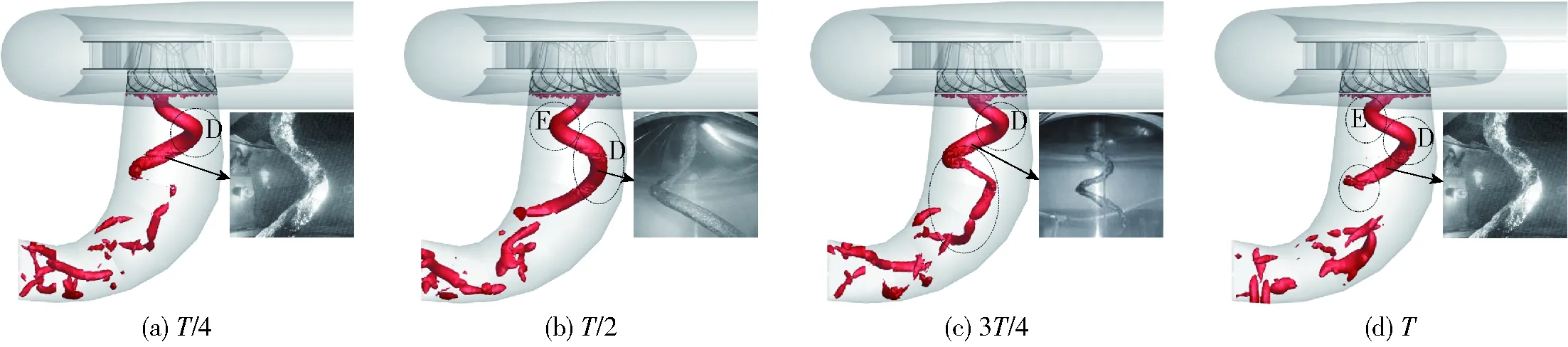
图12 αM=38.05 mm时尾水管涡带(Liutex值50)Fig.12 Vortex rope in draft tube under off-design condition of αM=38.05 mm (Liutex value is 50)

图13 αM=38.05 mm时尾水管子午面流线Fig.13 Velocity streamlines in draft tube under off-design condition of αM=38.05 mm

图12为导叶开度αM=38.05 mm工况下，沿轴线顺时针转动的螺旋涡带不同时刻的形态，可以观察到在该周期内螺旋涡带的形成、发展、转化和消散过程。与最优工况相比，此时在转轮出口处没有观察到轴对称的纺锤形涡带，仅有螺旋形和杂涡部分，且螺旋形涡带所占流域范围较广、形状变粗，破碎后的杂涡也较多。涡带在旋转下泄的过程中，偏心较大的D、E部位挤压尾水管近壁区域流体，进一步增大尾水管壁面脉动压力，极易引起机组振动。从图13该工况下的速度流线图也可看出，尾水管内出现螺旋状涡带，使得流动状态的轴对称性被打破，尽管尾水管内的水流仍以轴向流动为主，但是内部瞬时速度分布完全由涡带结构主导，围绕涡核附近，尾水管内出现了明显的旋转流动区域。旋涡在流速低于1 m/s时才会出现，此时速度降低，是由周向速度分量占优所导致。由于涡核附近为低压区，周围水流向该区域流动，而偏心涡带绕其自身转轴的旋转，进一步迫使周围水流作围绕涡带的旋转运动。与最优工况(图10)对比，尾水管整体流态差异较大，主要由于该工况涡带所占流域范围较广，加强了涡带对水流的排挤作用，使得涡带与壁面之间出现了明显的高速区，而且旋转流动区域附近高速区的强度和位置也随着涡带的时域变迁而改变，加剧了尾水管内整体流态的紊乱。

由此可知，在偏离最优开度时混流式水轮机转轮出口速度产生周向速度分量较大，导致水流在直锥段和弯肘段紊乱，产生较大的螺旋形涡带，且导叶开度越小，圆周速度分量就越大，涡带旋转半径越大，强度越大，即涡带偏心更严重，涡流结构对主流产生的干扰作用就越大，产生的涡流、回流和流动分离等不稳定现象越明显。引起的能量耗散、水力损失也越严重。

随着开度继续减小，不同负荷下的涡流结构差异较大，当导叶开度αM达26.17 mm时，螺旋形涡带继续变大，已经充据着整个直锥段和弯肘段，形成一个较大的空腔涡带，如图14所示。此时，由于转轮进口冲角过大，转轮出口绝对流动角方向也发生较大变化，引起了与转轮旋转方向相同或相反的绝对速度分量，流体圆周速度占优，形成紧贴壁面旋转下泄的流动状态。尾水管涡带由涡头到尾部整体呈锥形，即涡核偏心距沿直锥段和弯肘段呈线性增加趋势。在该工况下，涡带尾部的旋转运动直接冲击着肘管段内壁面，如图14中F位置所示，极可能导致强烈的噪声及压力脉动，产生这种强度的涡带，也会导致强烈的水力损失产生，这种发生在尾水管肘管段的异常现象被称为“冲击现象”[32]。此时相对流量约为最优工况下流量的55%。

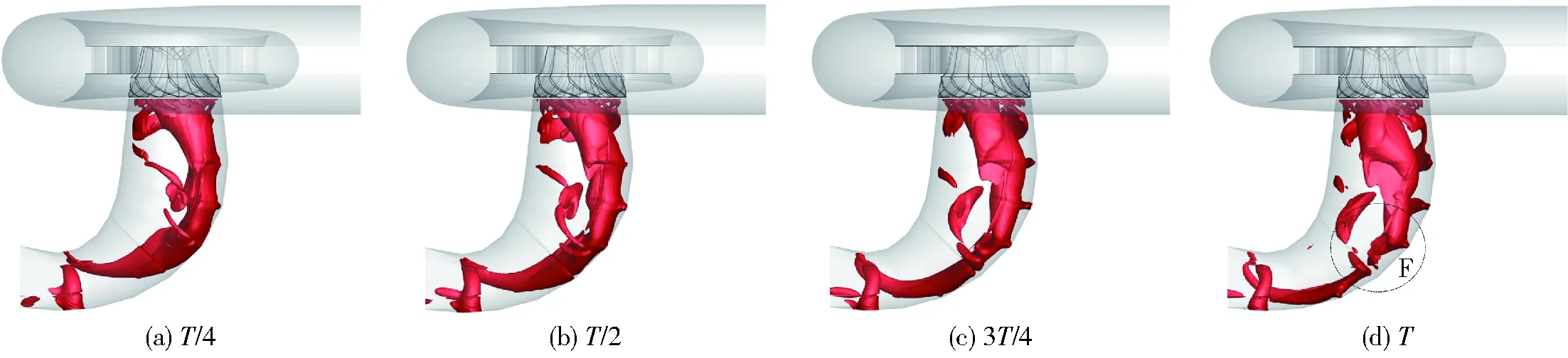
图14 αM=26.17 mm时尾水管涡带(Liutex值50)Fig.14 Vortex rope in draft tube under off-design condition of αM=26.17 mm (Liutex value is 50)

图15 αM=13.50 mm时尾水管涡带(Liutex值50)Fig.15 Vortex rope in draft tube under off-design condition of αM=13.50 mm (Liutex value is 50)

当导叶开度继续减小到最小开度时(αM=13.50 mm)，尾水管涡带没有继续增大，反而破碎成很多条极不稳定的小尺度拧旋流，相互影响交错。并且随着时间的推移，由明显的两条涡带(G、H)演化成4条涡带(G、H、I、J)相互转化、消散，极为杂乱，如图15所示。从该工况尾水管内的瞬时湍动能图(图16)也可以看出，开度过小时，由于杂涡过多，尾水管轴心区域不被有型涡带占据，反而近壁区内湍流加剧，湍动能最大达1.5 m2/s2，而轴心区域湍动能只有0.4～0.8 m2/s2，能量损失主要集中在近壁区，与最优工况(图11)相反。

2.3 尾水管压力脉动分析

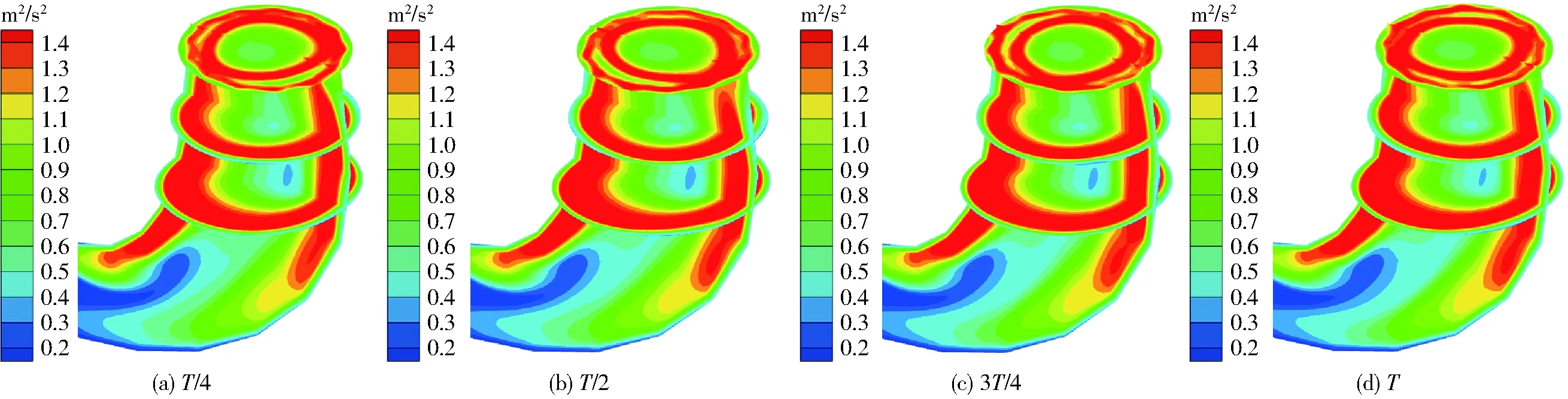
图16 αM=13.50 mm时尾水管子午面湍动能Fig.16 Turbulent kinetic energy in draft tube off-design condition of αM=13.50 mm

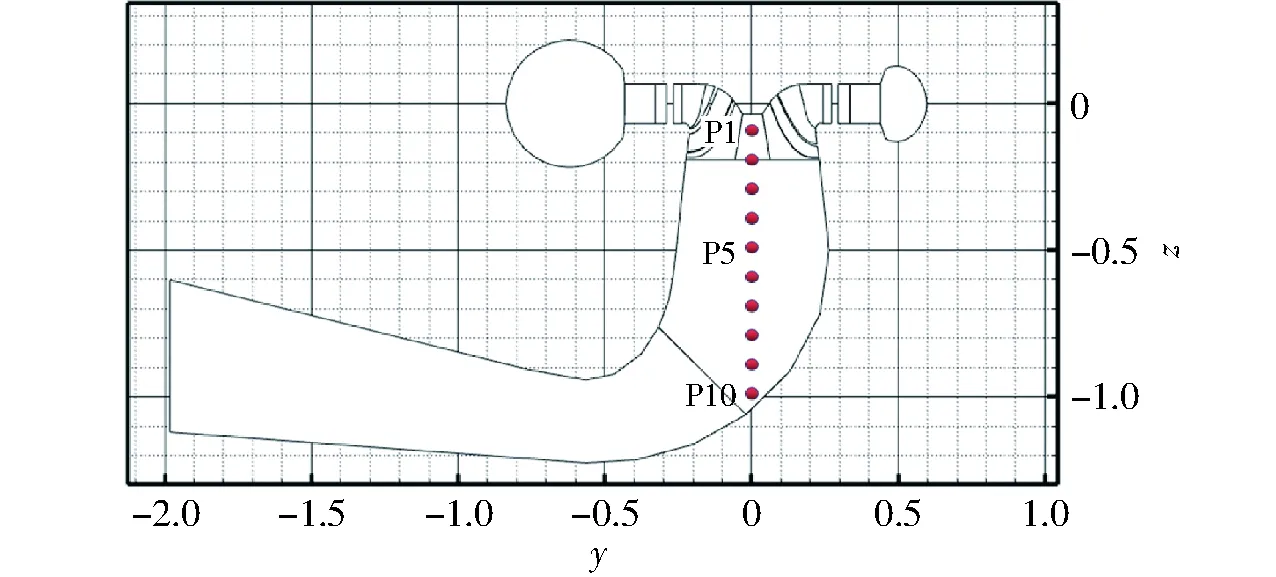
图17 尾水管流域上各监控点示意图Fig.17 Monitoring points in draft tube

图17(图中y、z分别表示流道展向、流向)为尾水管流域上各监控点示意图，为了探索泄水锥到尾水管弯肘段流域的压力脉动分布规律，在尾水管内部取了10个监控点，分别命名为P1～P10。

图18为以压力系数表征的压力脉动时域图(7个周期内)。从图中可以看出，不同工况下压力变化规律、大小均差异较大。同一工况下不同测点压力脉动系数波形几乎完全一致。在最优工况下，压力脉动呈明显的周期性变化。监控点P1位于泄水锥正下方，受上游转轮旋转影响较强，与尾水管内测点在幅值和相位上均有所偏差，如图18a所示。在偏工况下(αM=38.05 mm时)，尾水管涡带出现强烈偏心运动，使尾水管内压力显著变化，压力梯度增大，压力脉动系数在2.025 s处出现极大值点，说明压力的传递和变化受到尾水管涡带偏心旋转运动的影响。从图18b也可看出，点P1规律与下游各监测点同步性较好，不像最优工况点P1与尾水管内各点幅值和相位都有偏差，说明从泄水锥到转轮出口甚至整个尾水管流域都受到螺旋形偏心涡带的影响。

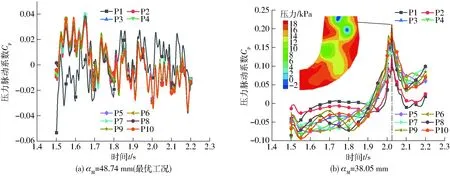
图18 尾水管压力脉动系数时域图Fig.18 Time-history curves of pressure coefficient in draft tube

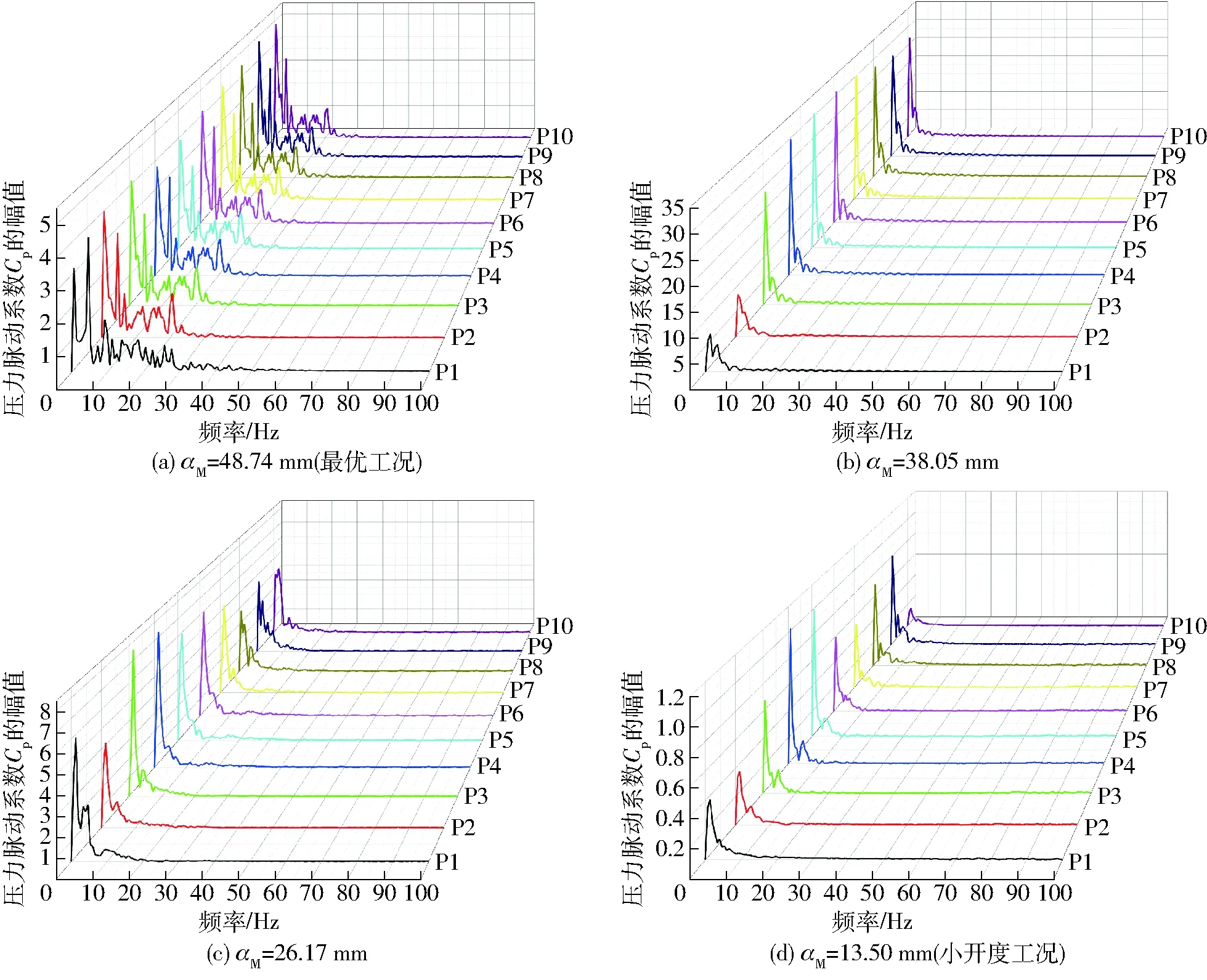
图19 尾水管压力脉动系数频域图Fig.19 Frequency domains of pressure coefficient in draft tube

图19为各测点压力脉动的频域结果，其主频统计结果如表1所示。从图19a中可知，在最优开度下，尾水管中没有受到偏心涡带的影响，但压力脉动频谱比较丰富，压力幅值低且上、下游变幅不大。当导叶开度αM减小到38.05 mm时，尾水管内产生了螺旋形偏心涡带，压力幅值突增，特别是尾水管内(P3～P10)压力幅值明显高于泄水锥内和转轮出口处，如图19b所示。当导叶开度继续减小，由于流量降低，压力幅值有所回落，如图19c、19d所示。从表1中可以看出，从转轮泄水锥到整个尾水管流域内均存在一个0.67 Hz的低频脉动。随着导叶开度的关闭，尾水管内出现涡带时，上游测点在频率为0.13fn时均出现压力系数的最大值(fn=10 Hz，为转频)，说明尾水管涡带压力脉动在低频时具有较高的能量，尾水管涡带压力脉动主频为1.33 Hz，为典型的低频特征。

为了进一步分析压力脉动幅值的变化趋势，采用脉动算术平均偏差Ra和最大脉动幅值Rz处理压力数值，定义式为

(5)

Rz=Cpmax+Cpmin

(6)

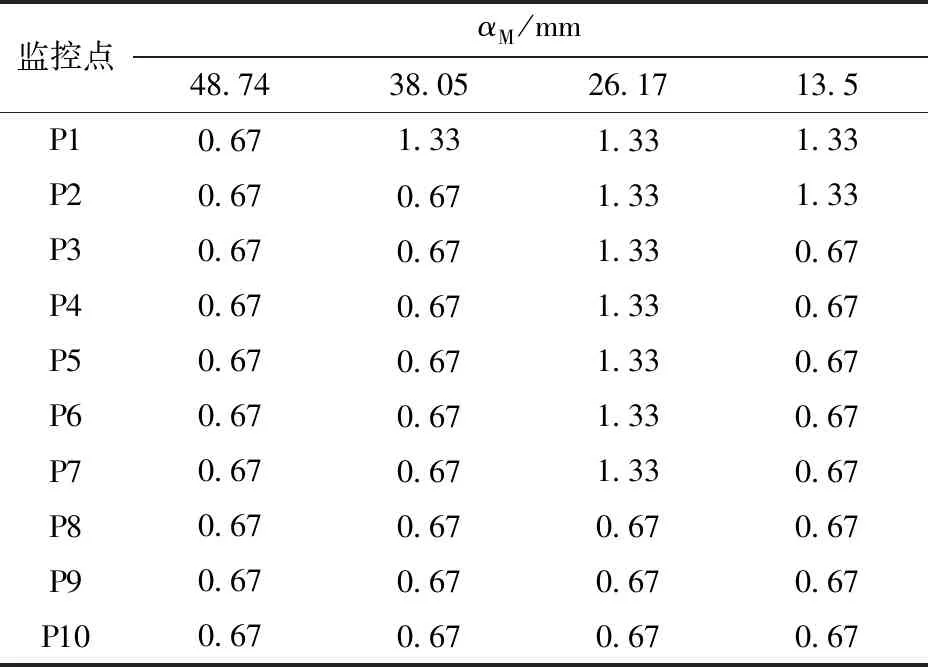
表1 尾水管监控点主频Tab.1 Main frequency of monitoring points Hz

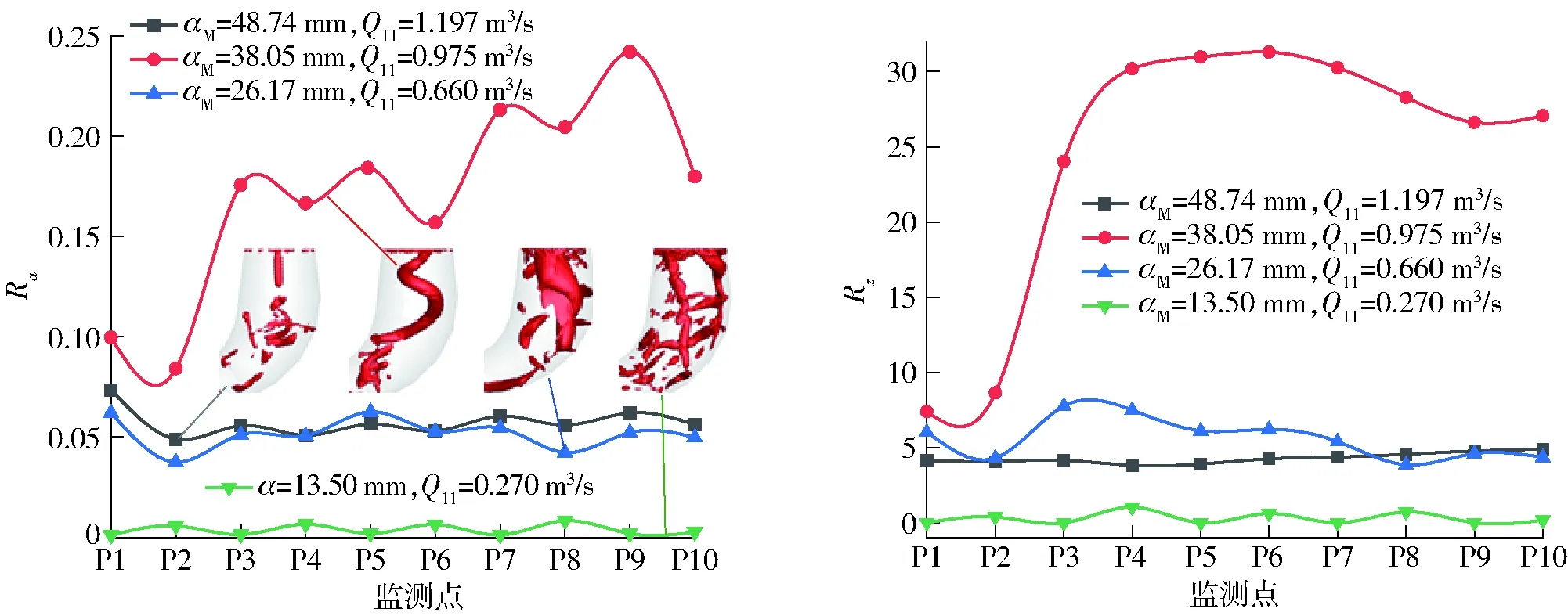
图20 脉动压力系数幅值Fig.20 Amplitude of pressure coefficient

式中n——监测时间段内脉动压力总数

图20(Q11表示HLA551-LJ-43模型水轮机的单位流量)为不同开度工况下Ra和Rz的变化曲线，从图中可以看出，在导叶开度为38.05 mm时，Ra和Rz远大于其他工况，平均脉动压力系数幅值比最优工况增加了1.36～4倍，偏心螺旋涡带的产生对尾水管内流场的干涉最强。随着开度的降低，αM=26.17 mm、αM=13.50 mm工况虽然也有不同形式的涡带产生，但此时流量较低，仅为最优开度工况流量的55%和22.5%，因此脉动幅值相对要低。说明尾水管偏心螺旋涡带运动产生的压力脉动的传递，是诱发水轮机水体共振的主要因素。