依托信息技术 深化函数概念*——以“生活中的变量关系”起始课教学设计为例

窦本旺 马 杰

(安徽省宿州学院附属实验中学,234099)

北师大版《普通高中教科书·数学》必修第一册第二章“函数”中的第一节“生活中的变量关系”是“函数”一章的起始课,具有统领本章的作用.这节课内容以复习为主,仅有“分段函数”一个新知识点.因此除了抓住教学中的重难点之外,还可借用互联网资源,有效用好教室中的希沃白板,丰富课堂内容,提升数学理解能力,培养学生学习数学的兴趣.本文对此进行探究.

一、教学设计

课前准备用希沃课件循环播放图片,内容包括欧拉、莱布尼茨、李善兰三位数学家的简介和重要成就.

设计意图营造数学课堂氛围,这三位数学家在数学领域有很大的成就.欧拉、莱布尼茨对现代函数的定义发展具有重要的推动作用,我国清朝数学家李善兰翻译的《代数学》,促进了中国近代数学的发展.

1.创设情境,回顾概念

利用希沃白板播放《乌鸦喝水》的视频.

问题设计生活中经常见到一些相互关联的变量,这是小学时我们学过乌鸦喝水的故事,你能从这故事中,找出哪些是常量?哪些是变量吗?你是如何判断的?

预设回答常量有瓶子的体积、高度、瓶口的大小等,变量有水的高度、石子的数量等.在变化过程中数值始终不变的量叫做常量,数值发生变化的量叫变量,变量又可以分为自变量和因变量.

设计意图从熟悉的故事出发,建立数学场景,复习常量、变量、依赖关系,引入新课.培养学生用数学的眼光观察、分析生活中的现象.让学生知道在一个变化过程中,哪些数值改变,哪些数值不变,以此可以分辨出来常量、变量、依赖关系等.

2.展示材料,深化概念

例12018年12月,我国高速公路总里程数为14万公里,位居全球第一,近两年里程数仍在递增.截止2020年年底,我国的公路总里程为519.81万公里,其中高速公路里程为16.1万公里,极大地促进了我国经济的发展.为了安全和节约空间,高速公路上常见的加油站经常在地下建造圆柱体储油罐储存汽油.如图1，已知该储油罐的长度d，截面半径r是常量,油面高度h,油面宽度w，储油量V是变量.

问题设计储油量V与油面高度h有依赖关系吗?与油面宽度w呢?V与h和V与w之间的依赖关系有不同之处吗?

预设回答储油量V与油面高度h存在着依赖关系,也与油面宽度w存在着依赖关系.对于油面高度h的每一个取值,都有唯一的储油量V和它对应.但是,对于一个油面宽度w的值,却对应着两个不同的储油量V.

例2自2008年京津城际列车开通运营以来,高速铁路在中国大陆迅猛发展,和谐号、复兴号等已成为一张靓丽的中国名片.截止2017年年底,中国高铁运营里程突破25 000 km.现正建设以八横八纵为骨架的高速铁路网.图2表示的是中国高铁年运营里程的变化.

问题设计根据图2,高铁运营里程与年份之间存在着怎样的依赖关系?从图2可以看出增长最多的是哪一年吗?

预设回答随着时间的变化,高铁运营里程也在变化,它与年份存在着依赖关系,从2008年到2017年,高铁运营里程是不断增加的,与前一年相比,2014年增长得最多.

设计意图通过这两个材料,让学生回顾两个变量之间的依赖关系,培养学生的读图、识图的能力,为理解函数关系创造条件.

问题设计你能回忆出初中阶段函数的定义吗?根据函数的概念，你能指出例1与例2中,哪些依赖关系是函数关系?为什么?

预设回答有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,那么y就是x的函数,其中x是自变量,y是因变量.

在例1中,由于油面高度h的每一个取值,都有唯一的储油量V和它对应,因此储油量V是油面高度h的函数.而取一个油面宽度w的值,对应着两个不同的储油量V,所以储油量V不是油面宽度w的函数.同理,在例2中,高铁运营里程是年份时间的函数.

设计意图通过追问,让学生体会依赖关系和函数关系的联系与区别,从而更好地把握函数概念的本质.

小结函数概念中需注意:凡是要确定两个变量具有函数关系,就要判断“对于变量x的每一个值, 变量y都有唯一确定的值和它对应”.若两个变量之间存在依赖关系,且对于其中一个变量的每一个值都有另一个变量的唯一值和它对应,则这两个变量之间具有函数关系,所以,依赖关系不一定是函数关系,但函数关系一定是依赖关系;研究函数关系时,通常要指明自变量和因变量,因为两者交换位置后不一定还存在函数关系.

3.阅读材料,理解本质

例3弹簧的伸长量x与弹力y满足函数关系y=kx,其中k为劲度系数.

例4表1记录了几个不同气压下水的沸点:

表1

例5绿化可以改变小环境气候.某市有甲、乙两个气温观测点,观测点甲的绿化优于观测点乙,图3是这两个观测点某一天的气温曲线图.为了方便比较,将两条曲线画在同一直角坐标系中.

例6某地电力公司为鼓励市民节约用电,采取阶梯电价,即按月用电量分段计费办法.居民每月应缴电费y(单位:元)与用电量x(单位:kW/h)的关系是

函数的图象,如图4.

预设回答在例3中,对于变量“伸长量”的每一个值,变量“弹力”都有唯一确定的值和它对应,弹力y是伸长量x的函数.在例4中,对于变量“气压”的每一个值,变量“沸点”都有唯一确定的值和它对应,沸点是气压的函数.在例5中,每一条曲线都表示了一个函数关系,反映的都是对于“时间”的每一个值,都有唯一确定的“气温”值和它对应.因此,每一条曲线都表示“气温”值是“时间”的函数.在例6中,对于变量“用电量(x)”的每一个值,变量“应缴电费(y)”都有唯一的值与之对应,所以应缴电费是用电量的函数.

例3是用解析式表示函数;例4是用列表法表示函数;例5是用图象法表示函数;例6既用了解析式又用到图象法表示函数,其中例6的解析式是分段函数.

设计意图初中数学教材中已学习过函数的三种表示方法,教材故意设计包含三种不同的表示方法的背景材料,用直观的内容帮助学生回忆函数知识,例6的设置引出分段函数的概念,也比较自然,为接下来的学习作充分的铺垫.

4.课堂总结,整体把握

利用希沃白板展示思维导图(如图5).

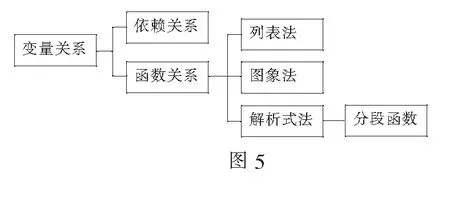
设计意图让学生对本节内容有一个整体的认识,培养学生利用思维导图领会数学知识的习惯,提升学生的逻辑思维能力.

5.布置作业,强基固本

(1)习题2-1A组第1,2,3题;

(2)拓展作业:从网络上或图书馆,学习函数的起源、发展历程方面的资料.

二、教学思考

1.培养学生用数学的眼光观察世界

“数学源于对现实世界的抽象”[1].本节所有例题中的材料背景,都与实际问题有关,体现了数学与生活密切关联性,说明生活处处皆数学，只要有一双发现数学的眼睛,就能从实际问题中,抽象出依赖关系、函数关系,特别是在内容安排上“蕴知识于无形”,自然地呈现出函数的三种表达方法,促进对数学概念的理解,培养学生的直观想象和数学抽象素养.

2.内容的安排符合知识的发展脉络

函数是中学数学中的核心概念之一,德国数学家克莱因曾说过:“函数是数学的灵魂”.函数的概念,也是学生进入高中阶段遇到的第一个较难理解的知识点,因此教材为了化解难点,特意安排本节内容,这也符合函数自身的发展历史,由18世纪中期的“变量依赖”说,到19世纪的“变量对应”说,再到20世纪后演变成“集合对应”说[2].这种安排促进学生对函数知识的建构,符合螺旋上升获得知识的规律.

3.希沃白板的运用提升教学效率

在电子技术的运用上,希沃课堂里面资料丰富,包含图片、音频、视频等素材,情境优美,功能强大,既能扩大课堂容量,又能拓宽数学教学空间.现代信息技术的有效运用,对积极调动学生探索知识的欲望,激发学生的深度思考,培养学生思维的深刻性、创造性,深化函数概念的理解提供技术支持.

4.材料的设置激发学生的民族自豪感

例题材料的背景中有高速公路建设、高铁的风采、气温测量和电力分配的智能化,既能从数学的角度理解函数概念,又展现社会主义建设的伟大成就,增强学生的民族自豪感,对坚定中国特色社会主义的“道路自信”有着重大意义.

“单薄”的教学内容如何上出“丰满”的教学效果？这就需要有把握课程的全局视野.优化课程结构,精选数学内容,突出教学主线,既要从知识的发展脉络讲解,又要从学生的发展去设计教学,树立“学生为本”的理念,只有充分理解教材背后的设计意图,才能取得良好的教学效果.“万山磅礴,必有主峰”.本节的“主峰”就是利用详实的材料,凸显函数的内容脉络,培养学生的数学理解能力,这也符合章建跃教授所讲的“四个理解”即理解教材、理解数学、理解学生、理解技术的教学理念.