探究习题教学策略 提升数学核心素养——由教材的一道课后习题引发的思考

何佩姬

(广东省清远市佛冈县佛冈中学,511600)

《普通高中数学课程标准》(2017年版)(以下称“课程标准”)指出:“高中数学教学以发展学生数学学科核心素养为导向,启发学生思考,引导学生把握数学内容的本质,提倡独立思考、自主学习、合作交流等多种学习方式,激发学习数学的兴趣,养成良好的学习习惯,促进学生实践能力和创新意识的发展”[1].数学习题是教材的重要组成部分,是数学教学过程中组织学生学习、实践活动的一种重要形式[2].因此，如何在解题教学中培育学生的数学核心素养，值得积极探究.

本文以新教材人教A版普通高中教科书必修第一册(简称“教材”)的一道课后习题为例,探究数学习题教学策略.

一、教学过程

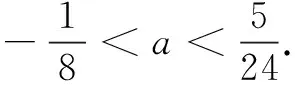
从学生完成的情况来看,基本都能得出“此题是不正确的”的结论,并找出一些不正确的理由.此题看起来简单,但易错,绝大部分的同学考虑不全面,出现“漏解”.针对此情况,笔者让学生投影解答过程的同时分享解题思路.

首先，利用随机抽检法抽到学生L.该同学说出了此题的错因，但只考虑了函数f(x)=24ax2+4x-1在区间(-1,1)存在零点,而没有考虑到函数在区间(-1,1)恰有一个零点,说明该同学对函数的零点存在性定理理解得不够透彻.

接着,请学生T到讲台来讲评其做法.其解答大致如下:函数f(x)=24ax2+4x-1在区间(-1,1)恰有一个零点,即函数图象在(-1,1)与x轴有唯一交点,即方程24ax2+4x-1=0在(-1,1)恰有一个解.

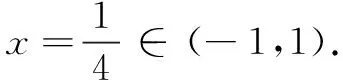
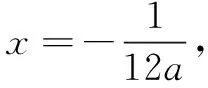
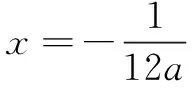
T刚讲完他的解题思路和过程，学生Y说“老师,这道题目还可以再简化,把a>0和a<0两种情况统一为一种情况.”,其解答过程如下:

(2)当a≠0时,Δ=42-4×24a×(-1)=16+96a.

在肯定Y的同时，指出这两个同学乃至班上绝大部分同学考虑不全面,漏解，由此引起学生的认知冲突,他们陷入了思考.这时适时提示要认真审题,借助图象看看还漏了什么情况.通过深入思考以及与同学间的相互交流，产生思维碰撞，把学习探究引向深入.

“老师,我有另一种解法,可以分享一下吗?”Z的解法如下:函数f(x)=24ax2+4x-1在区间(-1,1)恰有一个零点.则函数g(x)=24ax2与h(x)=-4x+1的图象在区间(-1,1)恰有一个交点.

(2)当a≠0时,函数g(x)=24ax2与h(x)=-4x+1的图象相交,其中必有一个交点落在区间(0,1)内，要保证两函数图象在(-1,1)只有一个交点,需满足:

接着总结说:“我的解法是将一个函数拆成两个熟悉的函数来研究,把函数的零点问题转化为两个函数的图象的交点问题.”

针对学生总结的易错点,展开提问:在原题的基础上,如果将“函数f(x)=24ax2+4x-1在区间(-1,1)恰有一个零点”改为“函数f(x)=24ax2+4x-1在[-1,1]恰有一个零点.”你会做吗?并进一步提问:你们还会将这道题进行改编吗?一石激起千层浪,学生有的说出:在原题的基础上,将“函数f(x)=24ax2+4x-1在区间(-1,1)恰有一个零点”改为“函数f(x)=24ax2+4x-1在区间(-1,1)有两个零点”等.这些变式题留作学生课后思考完成.

二、总结反思

1.精心设置习题,提高练习的有效性

本课所选的习题是教材课后的一道拓广探索题,该题围绕函数的零点的概念以及函数零点存在定理,考查学生的逻辑推理能力、运算求解能力以及灵活解决问题的能力.本题解法多样,为学生综合运用所学知识创造了条件,使不同思维水平的学生都得到充分展示.同时此习题给出的范围是(-1,1),学生容易漏掉f(-1)f(1)=0的情况,是易错题.为此,笔者选了此题给学生作为课堂的练习题.

2.暴露思维过程,重视过程性评价

本节习题课以学生为主体,教师为引导,鼓励学生分享其解题思路,暴露其思维过程.让学生经历作图分析,增强运用几何直观思考问题的意识;学生通过有逻辑地表达与交流问题,形成有条理的思维品质;通过数学运算促进数学思维发展,养成一丝不苟的好习惯在探索本习题的过程中,有意识地让学生“试错”,投影学生的错误“漏解”,教师把“生成过程”看作教学契机,并从学生的最近发展区入手,逐步打开学生的思维,引发学生进行交流讨论“漏了哪些情况呢?”学生情绪高涨,带着疑问深入思考,碰撞出智慧的火花,并大胆地展示了自己心中的想法学生从失败中找到通向成功的“门槛”,进行认知策略的学习,促进了逻辑推理、直观想象数学核心素养的发展.

本案例中,教师及时给予学生激励性评价,并对错解或漏解的同学进行鼓励,通过过程性评价使学生感受到学习数学的成就感.

3.注重变式探究,发散学生思维

本案例中,将原题的条件进行变动,引导学生对比原题进行解题,并鼓励学生主动参与到变题中来,然后再完成变式训练,这样能更好地发展学生的思维．本节课由一道习题,学生一触即发,掌握函数零点的基本解题规律,并在学习过程中体验改编习题的乐趣,从而达到让学生触类旁通的目的,提升数学核心素养.

4.引导总结反思,提炼思想方法.

本案例中,引导学生自主总结学习此习题涉及到的基本知识和思想方法,并在班上进行分享.由于学生已经经历了探究、分享解题思路的过程,学生很快就可以总结出解决本习题的通性通法,有的学生还不忘说出本习题的易错点.在教师的引导下，学生经历梳理知识、提炼方法、感悟思想的探究过程，提升逻辑推理、直观想象和数学运算素养.从而培养学生的概括总结能力，使学生对解题方法由感性认识上升到理性认识，会做一道题，掌握一类题，完成思维品质的提升.

通过优化习题教学的策略,学生在获得数学基本知识、基本技能的同时,进一步感悟数学思想方法,发展逻辑推理、直观想象等数学核心素养.习题教学要以发展学生数学学科核心素养为导向,精心创设习题,启发学生思考,暴露学生的思维过程,引导学生做好总结反思,增强学生学习数学的信心,树立敢于质疑、勤于思考、严谨求实的科学精神,培养学生良好的数学学习习惯.