圆盘剪用YC1钢的热变形行为及热加工图

2022-08-03霍庆辉汪宏斌

上海金属 2022年4期

刘坚霍庆辉汪宏斌陈卓

（上海大学材料科学与工程学院，上海 200444）

LD钢（7Cr7Mo2VSi）是由上海材料研究所研制的高强韧冷作模具钢，具有良好的耐磨性，被广泛应用于冷冲、冷锻以及剪切刀具等产品[1-2]。目前，有关LD钢的研究主要集中在表面改性[3]、热处理工艺[4-5]、切削加工性能[6]、激光表面熔凝[7]等方面，有关LD钢的热变形行为和热加工性能的研究较少。而本文选用的圆盘剪用YC1钢是在LD钢的基础上调整化学成分而研制成的，研究YC1钢的热加工性能对优化该钢种的热加工工艺及制定最佳锻造工艺参数具有指导意义。本构方程模型已经用于研究金属及合金的加工性能[8-10]，并且能够准确地预测其流变应力，其中Arrhenius模型应用较为广泛。此外，热加工图也已经广泛应用于铝合金[11]、合金钢[12]、钛合金[13]等材料。

本文采用Gleeble-3500热模拟试验机对YC1钢进行单向恒温热压缩试验，获得YC1钢的真应力-真应变曲线。为准确预测不同变形温度、应变速率及应变量下流变应力，基于传统的Arrhenius模型[14]，对流变应力本构方程进行改进。根据动态材料模型（dynamic materials model，DDM）[15]绘制YC1钢的热加工图，确定其最佳热加工区间，为生产中锻造工艺的制定提供试验及理论依据。

1 试验材料与方法

试验材料为圆盘剪用YC1工具钢，化学成分如表1所示。

表1 YC1钢的化学成分（质量分数）Table 1 Chemical composition of YC1 steel（mass fraction） %

采用线切割切取φ8 mm×12 mm圆柱体试样，表面打磨并抛光。在Gleeble-3500热模拟试验机上进行单向恒温热压缩试验。为减小夹头与试样之间的摩擦，在夹头和试样之间涂抹润滑剂并加一层0.1 mm厚的钽片。将试样以10℃/s的速率加热至1 130℃，保温3 min，使试样组织和成分均匀化，再以10℃/s的速率分别冷却至970、990、1 010、1 030、1 050 ℃，保温2 min 使试样成分均匀，然后分别以0.01、0.05、0.1、1 s－1的应变速率进行等温压缩变形。

2 试验结果与分析

2.1 真应力-真应变曲线

YC1钢的真应力-真应变曲线如图1所示。在热加工过程中，同时存在着因变形产生的加工硬化及动态回复和再结晶引起的动态软化过程。由图1可以看出，在变形初期，随着真应变的增大，流变应力迅速增大，这是因为位错的产生和增殖造成位错密度迅速增加而产生加工硬化；而此时由刃型位错的攀移和螺型位错的交滑移使位错密度不断减小而造成的软化作用较小。在流变应力达到峰值后，曲线趋于平缓或略微下降，这是因为加工硬化和软化作用达到了动态平衡[16]。

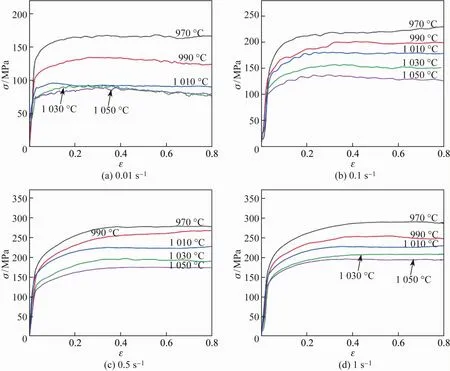
图1 不同应变速率下YC1钢的真应力-真应变曲线Fig.1 True stress-true strain curves of YC1 steel at different strain rates

应变速率相同时，随着变形温度的升高，流变应力减小，如图1所示。这是因为随着温度的升高，原子的活性增大，试验钢动态再结晶形核及长大速率增大，软化作用显著，流变应力减小。变形温度相同时，随着应变速率的减小，试验钢有较多的时间发生动态回复和动态再结晶，软化作用增大，流变应力减小。

2.2 流变应力本构方程的构建

双曲线正弦Arrhenius模型被广泛用来描述流变应力、变形温度与应变速率之间的关系[17-18]。为预测不同变形参数下YC1钢的变形抗力，构建了YC1钢在真应变为0.5时的双曲正弦型Arrhenius高温本构方程。其表达式为：

综合考虑变形温度和应变速率的影响，联立式（1）和式（5）可以得到：

然而，利用Arrhenius模型构建多应变量下的流变应力本构方程有明显的局限性。为了解决上述问题，相关文献对Arrhenius本构模型进行了改进[20]。

Lin等[21]采用应变补偿法对Arrhenius本构方程进行了修正，能很好描述42CrMo钢的变形行为。本文根据热压缩试验得到的YC1钢的真应力-真应变数据，对Arrhenius模型进行改进，分别取真应变为0～0.8间间隔为0.05的真应力，求得热变形激活能Q以及材料常数α、n、ln A，以真应变0.5为例，求解4个参数的过程如下：

对式（2）、（3）两边取对数得：

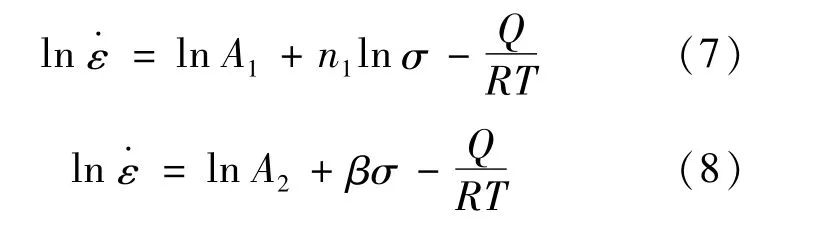
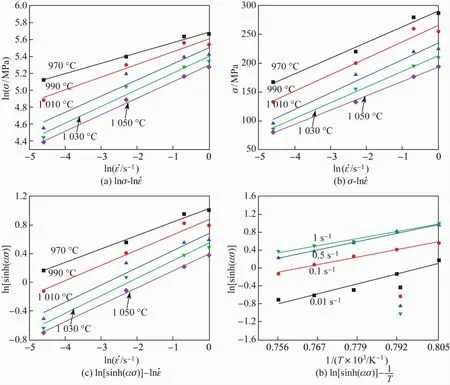
图2 真应变为0.5时YC1钢的不同热变形参数的关系曲线Fig.2 Relationship curves between different hot deformation parameters of YC1 steel at true strain of 0.5

对式（3）两边同时取对数得：

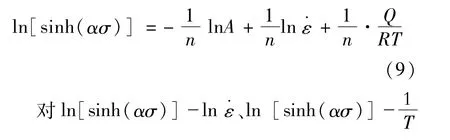
进行拟合，结果如图2（c，d）所示，可得出应力指数n＝4.501，表明试验钢的蠕变行为以高温攀移为主[22]。热变形激活能Q ＝564.703 kJ/mol，表明试验钢热变形抗力大，热加工难度大。

对式（6）两边同时取对数得：

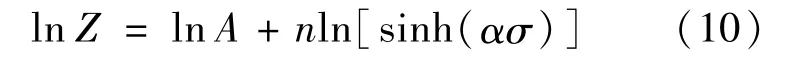
对lnZ － ln[sinh（ασ）]进行拟合，结果如图3所示，得到的线性相关系数为0.975，说明拟合结果准确度较高。通过拟合曲线得到截距ln A为49.862，材料常数A为4.52×1021。

图3 真应变为0.5时lnZ与ln[sinh（ασ）]之间的拟合曲线Fig.3 Fitting curve between lnZ and ln[sinh（ασ）]at true strain of 0.5

按照求解真应变为0.5时的α、n、Q和A参数的过程，分别求出真应变为0.05～0.75时的4个材料常数与真应变之间的关系，如图4所示。对4个材料常数进行多项式拟合，其中6次多项式拟合结果具有最好的相关性。6次多项式（11）中的系数如表2所示。

图4 α、n、Q、lnA与真应变之间的关系Fig.4 Relationship between α，n，Q，lnA and true strain

表2 材料常数α、n、Q、lnA的6次多项式拟合结果Table 2 6th order polynomial fitted values of material constants α，n，Q and ln A

由双曲线正弦函数的定义式：

联立式（6）、式（11）、式（12）得到YC1 钢的改进Arrhenius型流变应力本构方程为：

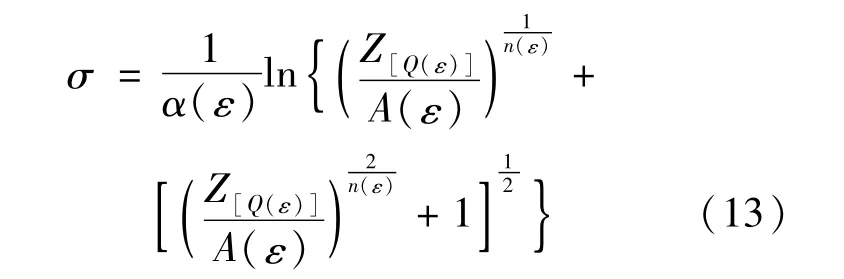
确定α、n、Q、A的值后，就可以确定不同应变量时的流变应力。联立式（5）、式（11）和式（13），则可预测不同变形温度、应变速率及应变量下的流变应力。为验证本构方程（式（13））的准确性，将不同变形温度、应变速率及应变量下的300个数据点绘制成试验值与预测值的关系图，如图5所示，得到流变应力试验值和预测值的相关系数为0.966，平均相对误差为5.1% 。

图5 流变应力预测值与试验值对比Fig.5 Correlation between the predicted and experimental values of flow stress

2.3 热加工图

为避开热加工的危险区，确定材料最佳的热加工工艺，以动态材料模型为基础绘制热加工图。热加工图由能量耗散图和失稳图叠加而成。DMM模型[15]认为，在材料变形过程中，外界对材料所做的功主要包括由加工变形造成的能量耗散和由组织变化造成的能量耗散两部分。功率耗散因子η的表达式为：

式中：m为应变速率敏感因子。通过真应力-真应变数据可以求出m，从而求出不同温度和不同应变速率下的η。试验钢在真应变为0.5时的三维功率耗散图和二维功率耗散图如图6所示。一般认为η值高的区域，材料的热加工性能较好，但不是所有η值高的区域都适合热加工，因为此区域有可能会发生塑性失稳。

文献[23]提出了材料在一定温度和应变速率下失稳的临界条件为：

将ξ随应变速率和变形温度的变化绘制成流变失稳图，ξ＜0的区域即为失稳区。将相同应变量下的功率耗散图和流变失稳图叠加在一起就构成了相应应变的热加工图。

YC1钢在真应变为0.5和0.7时的热加工图如图7所示。图中，灰色区域表示流变失稳区，在同一真应变下，灰度越浅说明ξ越大，等高线上的数字表示功率耗散因子η值。由图6可知，功率耗散因子的峰值出现在变形温度约1 010～1 030℃、应变速率0.01 s－1处，但结合流变失稳图发现该区域可能会发生塑性失稳。根据热加工图可知，YC1钢合适的热加工区间为变形温度1 030～1 050 ℃、应变速率0.01 ～0.13 s－1。