涡旋压缩机几何尺寸对流阻与传热的影响研究
2022-08-03侯军军刘忠良金银霞尹贺龙
李 超,侯军军,刘忠良,魏 宁,金银霞,尹贺龙
(兰州理工大学石油化工学院,甘肃 兰州 730050)
1 引言
涡旋压缩机是一种新型、高效、节能的容积式压缩机,具有结构简单、噪声小、振动低、效率高的特点[1,2]。涡旋压缩机工作过程中,涡旋压缩机的涡旋盘将会受到流体阻力作用以及传热的影响,这将会严重影响压缩机的工作效率。而涡旋压缩机的几何尺寸:基圆半径a、齿高h、壁厚t等都与涡旋压缩机的流动阻力损失以及传热存在一定的数学关系[3]。通过研究涡旋盘几何尺寸对涡旋压缩机流动阻力损失以及传热的影响,为涡旋压缩机的涡旋盘几何尺寸进行优化设计可以提供可靠的理论依据。
涡旋压缩机的几何参数影响着涡旋压缩机的容积变化和容积效率,因此对涡旋压缩机的几何尺寸的研究对提高涡旋压缩机的整机效率有着极其重要的意义[4]。顾兆林等从几个方面探讨了涡旋型线基本几何参数的选择问题,分析了型线几何参数对涡旋压缩机动力特性的影响[5];乔宗亮等从热力学第一定律出发,以能效比为目标函数、建立了包含压缩耗功、机械与电机损失、热与流动损失以及容积效率的数学模型,提出了涡旋压缩机优化分析模型[6,7];刘兴旺等在研究了几何参数对压缩机摩擦功耗和泄漏损耗影响的基础上,提出了一种新的涡旋型线设计方法[8];王君等通过研究工作腔内气体的周期性变化、涡旋齿与工作腔内气体之间的对流换热特点,采用数值模拟与理论分析相结合的方法,求解得到了涡旋齿侧壁面温度的变化规律,由此得到了涡旋齿的固体温度场分布规律[9]。
本文主要介绍了在吸气压力ps、行程容积Vs、压力比υ一定的情况下,不同涡旋压缩机型线几何参数对涡旋压缩机流动阻力损失以及传热的影响。
2 涡旋盘几何尺寸之间的关系
由于基圆渐开线的理论比较成熟且易于数控机床加工,所以目前常采用基圆渐开线作为涡盘型线。当采用如图1所示的圆渐开线作为动涡盘的涡旋型线时,设M为渐开线上的任一点,坐标为(x1,y1),φ表示与M点相对应的渐开角,a为基圆半径,则渐开线方程为

图1 圆渐开线
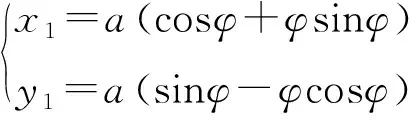
(1)
在吸气压力ps、行程容积Vs、压力比υ一定的情况下,由涡盘几何特征可得各参数之间的关系为
P=2πa
(2)
t=2aα
(3)
θ*=f(α)
(4)
(5)
(6)
式中P——涡旋体节距
a——基圆半径
t——涡旋体厚度
α——基圆渐开线起始角
θ*——开始排气角
υ——容积比
n——渐开线的圈数
θs——吸气角
h——涡旋齿高度
Vs——涡旋体的行程容积
由以上关系式表明:在吸气压力ps、行程容积Vs、压力比υ一定的情况下,节距P、壁厚t、齿高h均可以表示为基圆半径a的函数。
涡旋压缩机型线基本参数如表1所示。
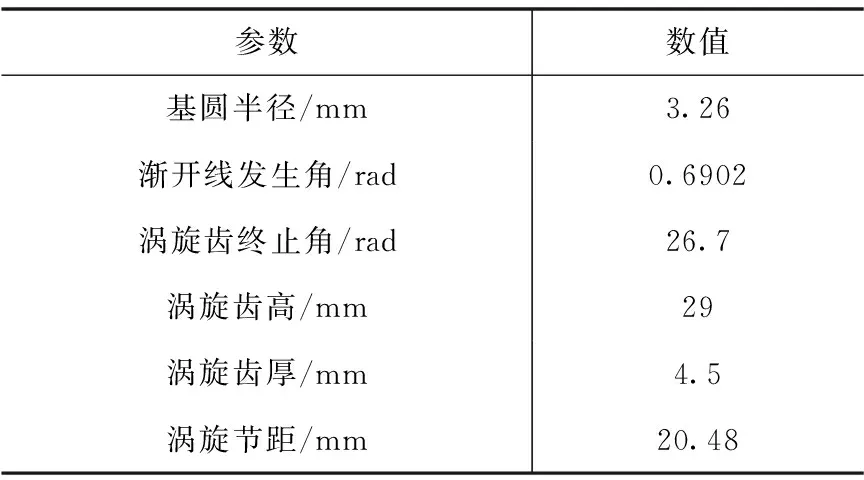
表1 型线及涡旋盘参数
3 涡旋压缩机几何尺寸与流动阻力损失的关系
在涡旋压缩机中,动涡盘的端板、十字滑环、平衡块等在运行过程中,将会受到流体阻力的作用。
当十字滑环等浸在油中时,还会有液体扰动损失。气体流动过程中,特别是通过狭窄通道流动时,还会引起气流摩擦损失[10]。
3.1 动涡盘运动引起的流动阻力损失
涡旋压缩机动涡盘的端板被置于静涡盘和支架之间,沿轴向留有很小的间隙,其外缘侧是具有一定压力的气体。因此当涡旋压缩机工作时,动涡盘端板的运动受到其外缘气体与润滑油混合物的阻碍,并由此引起流动阻力损失,损失的功率由下式计算
(7)
通过计算可以得到动涡盘运动引起的流动阻力损失Por与基圆半径a的关系式
Por(a)=f(a,α)
(8)
Por=ω3(πa-t)λ[2πa(2n+1)-t]
(9)
3.2 平衡块流动阻力损失
平衡块所在的空间是具有一定压力的气体、油或油气混合物,当平衡块随主轴一起做旋转运动时,流体的阻力损失可以由下式计算
(10)
式中PBl——平衡块流动阻力损失
HBl——平衡块的宽度
r1、r2——平衡块半径
CD——扰动系数
由上式可知,平衡块的流动阻力损失与涡旋盘几何尺寸无关,因此,可以忽略不计。
3.3 十字滑环引起的流动阻力损失
十字滑环运动时的流动阻力损失Pc为
(11)
通过计算建立十字滑环运动时的流动阻力损失P0与基圆半径a的关系式
(12)
3.4 气流摩擦阻力损失
在涡旋压缩机中,气体流动阻力在很多地方都会存在,但最大的气体流动阻力损失发生在排气孔口处。
3.4.1 中心压缩腔容积
一般情况下,圆的渐开线涡旋压缩机的第i个压缩腔容积为
(13)
对于中心压缩腔,它的容积与开始排气角θ*以及型线的修正情况有关。
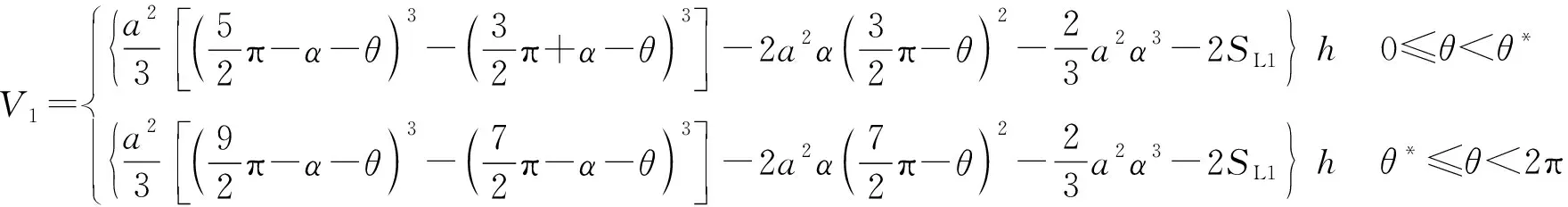
(14)
3.4.2 排气孔口处的气体流速u
根据连续性条件,通过排气口的气体流速u应满足下式
(15)
式中Ae——排气孔口有效流通面积
V1——中心压缩腔容积
对于圆渐开线,如果压缩机转速恒定,把表示中心压缩腔容积变化的关系式(14)以及θ=ωt代入式(15),经整理后可得
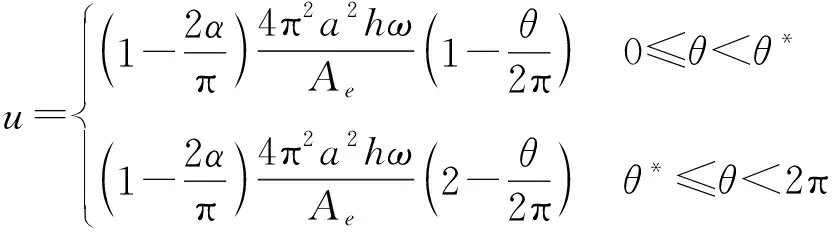
(16)
3.4.3 排气孔口处气流摩擦损失
通过排气孔口的气体流动,可近似地看作通过喷管的流动,则通过排气孔口处的气流摩擦损失Pfg为
(17)
将式(16)代入式(17)可得排气孔口处的气流摩擦损失Pfg关于基圆半径a的函数关系式
Pfg=f(a,t,θ)
Pfg=
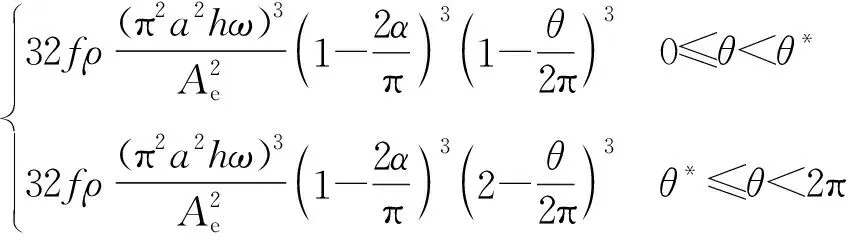
(18)
3.5 滑动轴承的摩擦损失
压缩机的主轴中心线与滑动轴承的中心线重合是非常困难的,由于加工误差和装配误差的影响,轴和轴承经常是偏心的。
轴颈的摩擦力矩为
(19)
式中μ——油的动力粘性系数
ω——主轴旋转角速度
R——轴颈半径
h0——滑动轴承径向均匀间隙
ε——滑动轴承与轴的相对偏心量
l——滑动轴承的长度(宽度)
主轴发生旋转时发生在滑动轴承处的摩擦损失Pτ为
Pτ=Mτω
(20)
由上式可知,滑动轴承处的摩擦损失,只与主轴旋转角速度等有关,与涡旋压缩机型线几何尺寸无关,因此可以不做过多考虑。
3.6 涡旋压缩机各部位流动摩擦损失之和
通过所求得的各个部位流动阻力损失,建立起总的流动阻力损失P0关于几何尺寸的关系式
P0=f(a,t,h)
P0=Por+PBl+Pc+Pfg+Pτ
(21)
由此可以得到流动阻力损失关于基圆半径的变化曲线,如图2。

图2 流动阻力损失
由图可知:涡旋压缩机工作过程中的总的流动阻力损失P0与基圆半径a变化关系曲线基本与动涡盘运动引起的流动阻力损失Por与基圆半径a的变化曲线相同;十字滑环运动时的流动阻力损失Pc和通过排气孔口处的气流摩擦损失Pfg与动涡盘运动引起的流动阻力损失Por相比几乎为零;因此,涡旋压缩机工作过程中的总的流动阻力损失P0主要以动涡盘运动引起的流动阻力损失Por为主。
4 涡旋压缩机几何尺寸对传热的影响
涡旋压缩机的工作过程中存在着许多换热现象,由于换热量的计算相当繁琐,就以涡旋压缩机的一个腔为例,研究它从吸气开始到排气结束,研究它与压缩腔外涡旋齿之间的对流换热量,确定涡旋盘几何尺寸与其换热量之间的关系。
4.1 径向泄漏线计算
对于圆渐开线的涡旋型线,分析渐开线的几何学理论,当主轴转角为θ时中心排气腔内通过轴向间隙的径向气体泄漏线的长度,即涡旋体壁厚的中心线长度。
圆渐开线的弧长,从基圆的起始点算起
(22)
径向泄漏线随转角θ的变化关系式为
(23)
4.2 工作腔外型线长度
研究工作腔与其外壁面的换热量,需要计算出外壁面型线长度,才可以得到换热面积,工作腔外型线长度变化曲线如图3。
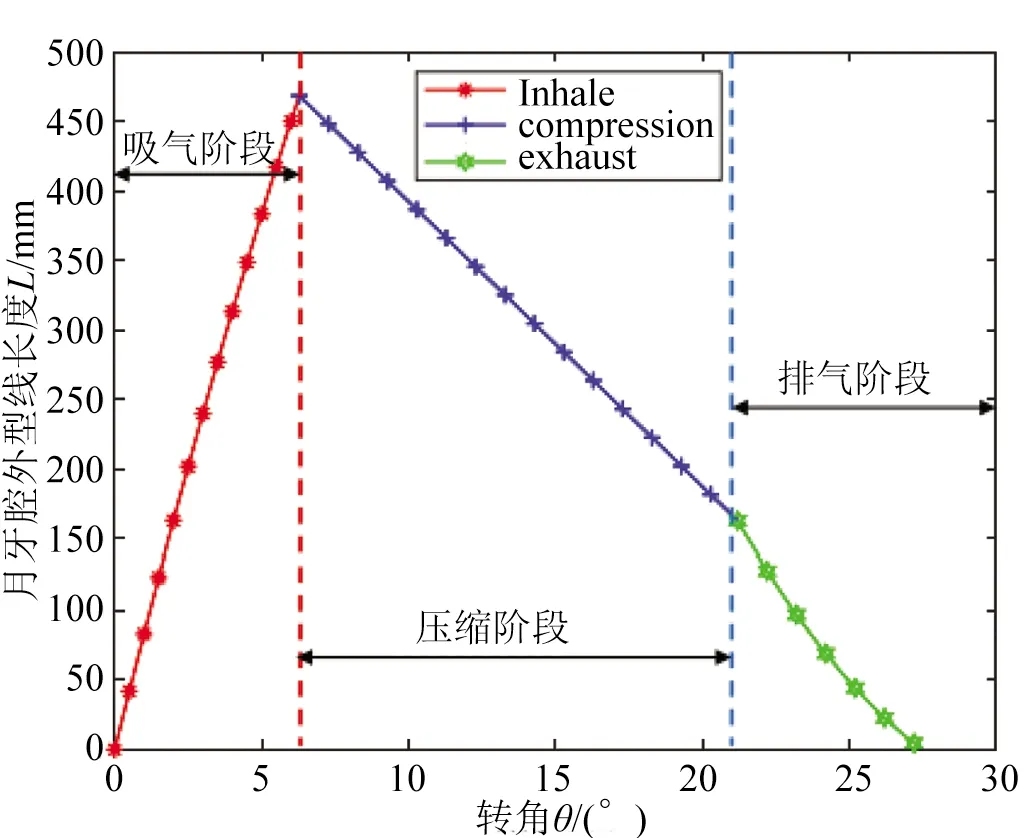
图3 工作腔外型线长度变化曲线
吸气过程
l=Lmax-l(θ,α)
(24)
压缩过程
(25)
排气过程
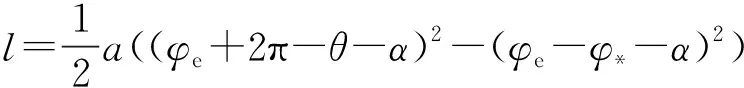
(26)
4.3 换热面积计算
由于在研究过程中只是单纯考虑工作腔从开始吸气到排气结束整个工作过程中工作腔与工作腔外壁面的换热量,因此对内壁面及腔底面积,忽略不计,只需要计算外壁面面积即可。
工作腔外壁面面积
A=lh
4.4 工作腔气体温度计算
姜营等以涡旋齿的圆渐开线展角为自变量,计算了月牙形工作腔容积[11]
(27)
由此可以得到任一转角下温度随转角变化关系为
(28)
工作腔气体温度变化曲线如图4。

图4 工作腔气体温度变化曲线
4.5 涡旋齿温度计算
涡旋齿壁与工作腔内气体之间的对流换热的热阻集中在热边界层,因此可以采用傅里叶导热公式,求解涡旋齿的温度。
(29)
式中q——热流密度
λ——对流换热系数
T——工作腔气体温度
TW——涡旋齿温度
δ——热边界层厚度
由此,可以得到涡旋齿温度随转角变化曲线如图5所示。

图5 涡旋齿温度变化曲线
4.6 换热量计算,如图6

图6 换热量变化曲线
涡旋压缩机工作腔的换热过程可以近似的看成平板对流换热,并满足Johnson-Rebesine方程式,因此,换热量为
Q=AhcΔT
(30)
由此,可以得到涡旋压缩机一个工作腔从开始吸气到排气结束整个工作流程下,换热量与几何尺寸的关系式
Q=f(a,t.h,θ)
(31)
5 涡旋压缩机几何尺寸对换热以及流阻的影响
以涡旋压缩机的主轴转角θ=3π为例,研究涡旋压缩机主轴转角在θ=3π的情况下,涡旋压缩机几何尺寸对流动阻力损失以及传热的影响关系。
5.1 瞬态换热量计算
在θ=3π时,我们可以得到涡旋压缩机工作腔外型线关于基圆半径a关系式
(32)
换热面积为
A1(a)=hL1(a)
(33)
由此,可以得到换热量Q关于基圆半径a的关系式
Q1(a)=A1hcΔT
(34)
(35)
由此可以得到在θ=3π时,涡旋压缩机工作腔外壁面换热量Q1随基圆半径a的变化曲线如图7所示:
由图7可知:在θ=3π时,涡旋压缩机工作腔外壁面换热量Q1随基圆半径a的增大而逐渐增大,两者成正比关系。

图7 换热量随基圆半径变化曲线图
5.2 流阻与换热之和与基圆半径a的关系
在θ=3π时,计算涡旋压缩机流动阻力损失与换热量之和W为
W=P0+Q1
(36)
旋压缩机流动阻力损失与换热量之和W与基圆半径a曲线关系如图8所示。
由图8可知:在涡旋压缩机主轴转角给定的情况下,流动阻力损失与换热量之和W随着基圆半径a的增大而逐渐增大;在流动阻力损失与换热量之和W中主要以涡旋压缩机总的流动阻力损失P0为主;在给定基圆半径a=3.26 mm时,所得到的流动阻力损失与换热量之和W=1.45×107J。
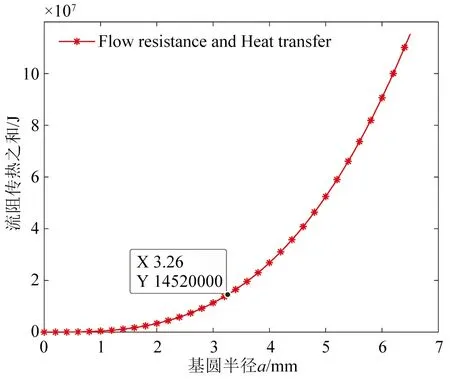
图8 流动阻力损失与换热量之和为随基圆半径变化曲线
6 结论
(1)在涡旋压缩机工作过程中所受到的各项流动摩擦损失中,受涡旋压缩机型线几何尺寸影响的有动涡盘运动引起的流动阻力损失Por、十字滑环运动时的流动阻力损失Pc、排气孔口处的气流摩擦损失Pfg。在这三处流阻中以动涡盘运动引起的流动阻力损失Por影响最大,其他两处几乎可以忽略不计;
(2)通过研究涡旋压缩机一个工作腔从开始吸气到排气结束的整个工作过程,得到了任一主轴转角下,涡旋压缩机工作腔气体与其涡旋齿壁面的对流换热量,并且得到了在任一转角下涡旋压缩机基圆半径a对其换热量的影响关系曲线;
(3)综合考虑涡旋压缩机型线几何尺寸对流阻以及传热的影响,可以得知涡旋压缩机型线几何尺寸对其涡旋齿壁面换热量的影响相较于涡旋压缩机流动阻力损失而言很小;
通过研究涡旋压缩机型线几何尺寸对涡旋压缩机流阻以及传热的影响,在考虑涡旋压缩机流阻以及传热的情况下,对涡旋压缩机型线几何尺寸优化提供了可靠的理论依据。
