基于傅里叶描述子的平面物体表征与抓取规划
2022-08-02许少秋陈根良唐楚禹
许少秋,陈根良,唐楚禹
(上海交通大学机械与动力工程学院,上海 200240)
0 引言
机器人技术是当今快速发展的新兴产业,其应用领域逐步从工业、农业走向服务业、医疗和物流等[1]。人们对机器人的要求朝着智能化发展,近几年内,机械手爪的结构设计、控制策略以及抓取规划成为国内外研究的重点[2]。
机械手爪的抓取规划指的是,以机械手爪的结构为基础,根据待抓取的目标物相关信息,计算机械手抓取目标物时最优的抓取姿态,从而实现稳定的抓取[3]。目前,采用基于物理模型的方法通常需要针对不同场景进行不同的简化假设,但随着机械手和目标物的形状的复杂化,其计算方法越来越复杂[4-6]。近年来,基于深度学习的抓取规划方法不断发展,但这类方法需要大量的训练数据,且其抓取模型通常较为简单,训练集的标注也需要大量人工时间[7-8]。
考虑到上述方法的缺点,本文基于傅里叶描述子对平面物体的统一表征,提出了一种计算抓取位姿性能评价指标的方法,在此基础上,采用优化粒子群算法实现了最优抓取点的规划。
1 平面物体的通用表征方法
1.1 图像采集与轮廓提取
采集待抓取物品的图像,并对其做如下预处理:
a.彩色图像的灰度化和灰度调节。将3维的彩色图像降为1维的灰度图像。
b.图像滤波。采用高斯滤波模板对前述图像进行滤波,可以消除图像中的部分噪点。
c.图像二值化。设定图像灰度阈值,将灰度大于该阈值的像素点设置为黑色,其余设置为白色,本文采用自动设置灰度阈值的方法。
d.图像开运算。考虑到处理过程中背景为黑色,物体为白色,对图像进行开运算,使得白色图像的边界更加连续。
在完成图像预处理后,本文采用边界提取效果较好的Canny算子[9]。Canny算子根据一阶偏导的有限差分计算图像的梯度,对梯度幅值进行非极大值抑制。完成轮廓提取后,即得到了描述图像轮廓的散点坐标。
1.2 基于傅里叶描述子的轮廓表征方法
计算出的轮廓散点仅能够体现哪些点在图像轮廓上,缺乏对物体轮廓连续的参数化表达,由于后续需要计算轮廓上任意抓取点的位置,因此需要将散点轮廓信息转化为参数方程来表示轮廓信息。本文采用傅里叶描述子来实现物体轮廓的表征,这一描述子常用于物体分类和图像分割。
傅里叶描述子的原理在于把平面任意闭合曲线上的1点看作无穷数目的定长向量首尾相连得到的末端,即每一后续向量均绕其前序向量末端为原点做圆周运动[10],因此可以用式(1)表示出该曲线上1点的坐标。
(1)
Ck为圆的半径;ek·2πit为向量绕其起始点旋转k·2πt的角度,由于考虑圆的顺时针和逆时针旋转,因此k取值范围为[-∞,∞],其数值越大表示该向量旋转速度越快,规定当向量C1旋转1圈后边界的点回到起始点,因此t取值范围为[0,1]。实际计算过程中无需无穷多向量,通常取正负K项作为边界轮廓的表征,即
(2)
如图1所示,轮廓由共5阶的傅里叶描述子组成,其中,C0为该轮廓的几何中心,其余Ck首位相连使得末端成为轮廓点。当式(1)中t取不同值时,可表达轮廓上不同的点,图1中标出t取2个不同数值时末端点的位置。

图1 傅里叶描述子
因为存在如下的积分关系有
(3)
所以式(2)中Ck的求解方法为

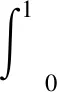
(4)
将式(4)由积分形式转化为多个点的求和,即
(5)
因此采用傅里叶描述子表述轮廓方程,其参数计算方式和离散傅里叶变换有一致性,即
(6)
由此可知,当共有N个离散的轮廓点时,最多可提取N-1阶的傅里叶描述子。通过傅里叶描述子计算曲线上任意点的坐标,与离散傅里叶反变换也存在对应性,即
(7)
需要将离散傅里叶变换中频率在[0,N-1]的幅值X(k)转换到傅里叶描述子中频率在[-K,K]的幅值Ck,因为存在如下关系:
f(n)ent·2πi=f(n)e(nt-n)·2πit=
(8)
所以傅里叶描述子和离散傅里叶变换中存在的转换关系为
(9)
1.3 实物图像验证
为验证傅里叶描述子对平面物体轮廓表征的可行性,本文利用抓取数据集Cornell与实拍的图像进行验证。实物图像验证流程包括:图像采集、图像处理、轮廓提取、傅里叶描述子计算、轮廓还原及实物对比,结果如图2所示。

图2 傅里叶描述子在实物图像的验证
由实验结果可知,本文采用的方法可以有效提取得到物体的轮廓边缘散点。提取参数幅值较高的正负各5阶傅里叶描述子来表征物体轮廓,反变换还原的轮廓和物体真实轮廓接近程度高,证明采用傅里叶描述子可以有效反映物体轮廓形状。
2 抓取性能评价指标的定义和计算
2.1 接触模型及抓取映射
手爪抓取过程中,需要首先确定手爪接触模型,即手指与物体具体的接触情况。通常将接触模型分为3种:无摩擦点接触、有摩擦点接触和软手指接触。无摩擦点接触即仅沿着法向施加压力;有摩擦点接触不仅有法向压力,还具有切向摩擦力;软手指接触则进一步考虑绕法向的转矩。通常,为统一表达接触模型,通常采用力螺旋基Bci∈Rp×mi和摩擦锥Ωci,其中针对空间抓取时p=6,针对平面抓取时p=3,mi为接触点处施加的独立力的维数[11]。如此,在接触点坐标系中的接触力Fci即可用力螺旋基Bci与力的大小fci相乘来表示,即
Fci=Bcifcifci∈Ωci
(10)
在进行抓取分析时,为确定各接触力对物体的影响,需要将接触力转换到物体坐标系。假设第i个接触坐标系{Ci}相对于物体坐标系{O}的位姿为goci=(poci,Roci),则该物体坐标系中的接触力Foi为
(11)

对于二维平面抓取,力螺旋变换矩阵为
(12)
由于同一坐标系中的力螺旋可以叠加,因此当有多个手指与物体接触时,物体上的总力螺旋可以表达为各手指施加的力螺旋之和。当共有k个手指接触时,则{O}中的合力螺旋Fo为
Fo=G1Fc1+…+Gkfck=
(13)
定义物体的抓取映射为G:Rm→Rp,所有力的大小为fc,即存在
(14)
由此,可以用抓取映射矩阵来表示多点接触抓取时的抓取位姿。相较于基于深度学习抓取规划中采用手爪中心点、抓取角度和手爪开口宽度等信息来描述抓取位置,采用抓取映射的表述方式具有明确的物理含义,针对不同形状的物体均可实现表征。
2.2 力-力矩空间中抓取性能指标定义
抓取规划的前提是对不同的抓取位姿区分其抓取性能,第1种是“0-1”的评价方法,第2种是定量的评价方法。前者计算简单,因为输出仅为0(失败)或1(成功),被基于深度学习的方法广泛使用。深度学习方法通常通过添加噪音,将形成力封闭的概率作为抓取性能。这种采用力封闭作为基础物理模型的评价,对于同样成功的抓取位姿,缺乏更进一步的评价。本文从完备的抓取模型出发,以抓取映射矩阵为基础,计算了一种在力-力矩空间中有物理含义的抓取性能指标。
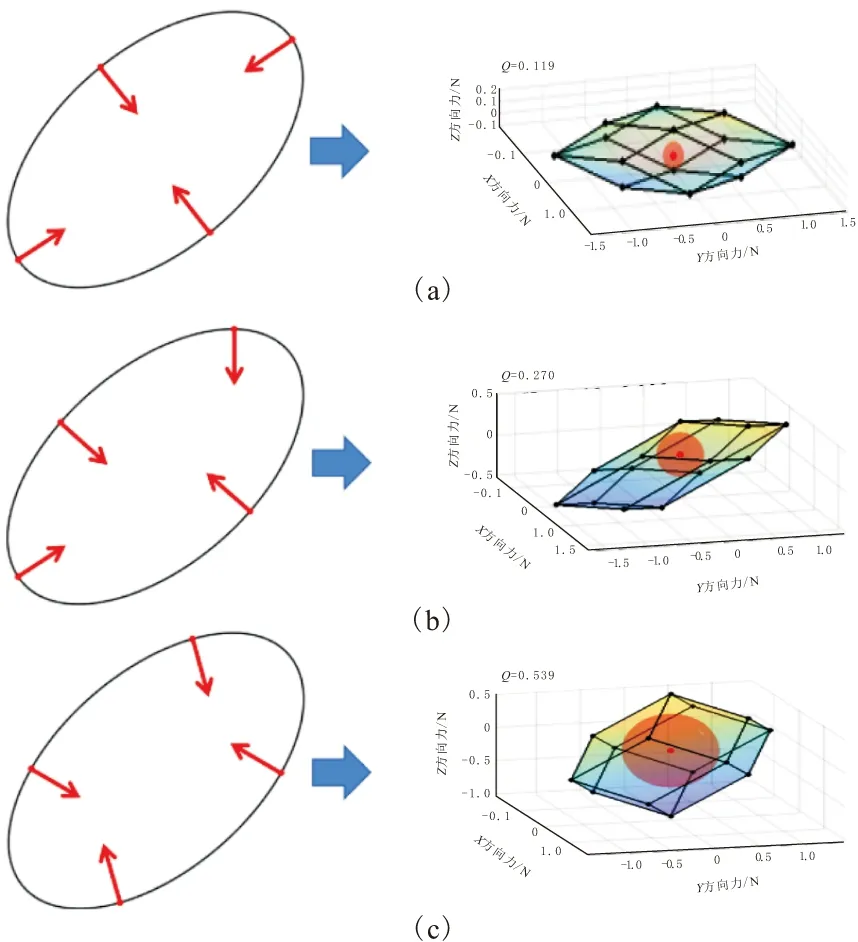
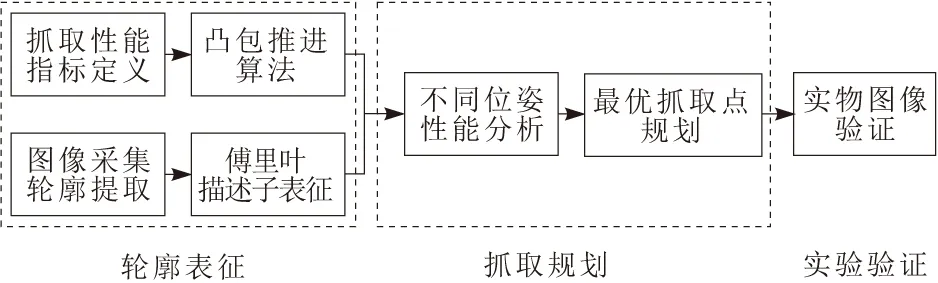
首先,假设每个手指施加的接触力上限均为1即为0 (15) i为第i个接触点;j为第i个接触点产生的第j个独立力螺旋;H()为由向量组成凸包。在无摩擦点接触模型中,式(15)可写为 P=H(G1…Gn) (16) Gi为抓取映射矩阵的第i列。得到凸包后,该抓取性能指标等价于原点到该凸包各表面最小距离,直观地可看作该凸包最大内切球半径[12]。如图3所示,当仅考虑物体抵抗平面受力Gi时,抓取性能指标Q表示为力平面上最大内切圆半径。 图3 平面受力抓取性能指标 当考虑空间受力时,由于3个单方向三维力能够抵抗的任意方向最大三维力螺旋为0。图4为3个大小范围在[-1,1]的力螺旋Gi产生的立体凸包及其对应的最大内切球。 图4 空间受力抓取性能指标 基于傅里叶描述子表述的物体轮廓,计算轮廓点切向方向u和法向方向v为 (17) 分量为 (18) r(Ck)为取其实部;i(Ck)为取其虚部,T=2πit。由此,式(12)中旋转矩阵为 (19) 本文考虑物体抵抗绕垂直于平面的轴的力矩的性能,因此凸包存在于力-力矩空间,故需要对其量纲进行统一。目前对力矩的处理方法仍无统一定论,根据文献[13],本文选用了在能量层面有物理意义的物体的回转半径作为归一化系数。基于上述公式,可以完成力-力矩空间中抓取凸包的计算,考虑平面抓取,式(16)转换为 (20) ρ为回转半径;Gij为矩阵G中的元素。 本文给定某一采用三阶级傅里叶描述子表述的曲线,其参数方程为 f(t)=(0.5+0.5i)e-1·2πit+ (1+1i)e0·2πit+(2+1.5i)e1·2πit (21) 本文采用4点无摩擦接触的方式,取参数t为不同值,得到的不同抓取点位置,生成3种不同的抓取点分布,并计算其对应的抓取映射矩阵,计算结果如图5所示。 图5 3种抓取点分布及其对应抓取映射矩阵 由于每个基础力螺旋均为三维向量,且凸包由多个力螺旋形成,采用逐个点搜索的方法构建凸包计算量大且效率低,并且判断其包络边界也需要较大的计算量。本文从几何角度出发,采用包络理论的边界推进算法,计算抓取力螺旋空间[14]。 边界推进算法将多个基础力螺旋看作依次作用、逐层包络。假设前k个力螺旋凸包计算后,其凸多面体用Pk表示,第k+1个力螺旋作记为Λk+1,则凸多面体Pk+1可以看作是Λk+1在Pk内部和边界上扫略而得到的空间区域,这种产生凸包的方式如图6所示。 图6 凸包边界推进理论 图7 2种凸包计算方法对比 图8 凸包顶点及面片结构 图9 情况或在包含的 图10 情况或在包含的 对Pk所有顶点逐一分析,即可得到Pk+1的所有顶点以及其之间的连接关系,实现的凸包的边界推进。最终,计算原点到凸包各面片的距离,取最短距离为最大内切球半径,即抓取性能指标,结果如图11所示。 图11 3种抓取点分布及其对应凸包和抓取性能 基于3种抓取位姿,分别计算其抓取性能指标,从图11可知,第3种的性能最佳,可以更好地抵抗外力。 粒子群算法是一种经典的优化算法,常用于非线性优化问题的求解。本文采用改进粒子群算法,以抓取性能指标为优化目标,设计了抓取规划方法,此方法流程如图12所示。 图12 抓取规划方法流程 在更新粒子速度和位置时,传统的计算方式为: (22) (23) 本文为避免该算法陷入局部最优,采用了一种动态改变惯性权重的改进粒子群方法[15]。其惯性因子计算方法为 (24) ωmax为惯性因子上限;ωmin为惯性因子下限;M为总迭代次数;k为目前迭代次数。 整体算法参数设定如表1所示[16]。 表1 算法参数值 本文总体的抓取规划流程如图13所示。 图13 抓取规划流程 针对式(21)描述的曲线,采用本文提出的规划方法,计算出其最优位姿、抓取映射矩阵及对应抓取性能指标如图14所示。 图14 最优抓取位姿 图15 3种位姿与最优位姿对比 二指平行夹持器是大多数深度学习抓取规划算法采用的执行机构,也是工业中常用的一种构型,本文将提出的抓取规划方法应用于两点接触模型中进行验证。 考虑到平面物体二指抓取需采用有摩擦点接触模型,因此在构造抓取映射矩阵时,本文将1个接触力等效为平面摩擦锥2条边界上的合力,从而可完成抓取凸包的构建和性能指标的计算。用2个摩擦合力代替1个摩擦点接触时,其合力的范围仅为真实合力范围的1/2,然而并不影响不同抓取位姿之间的抓取性能对比。有摩擦点接触模型等效如图16所示,其中,左侧Fz为正压力,μFz为摩擦力最大值,阴影区域为合力的范围;右侧Fz为正压力,f1和f2为用于构造抓取映射矩阵的等效力,阴影区域为合力的范围。 图16 二指摩擦点接触等效模型 本文在Cornell抓取数据集上进行实验,选取该抓取数据集中近似于平面物体的图像共154例,其典型结果如图17所示。 图17 二指抓取规划结果 实验共涉及的物品种类包括家用物品、文具、食品、洗浴用品等,在154个算例中计算成功率为87.01%,各类型规划成功和失败个数如表2所示。 表2 二指抓取规划成功率(不同种类) 针对平面物体抓取,对于非异常曲面,采用四点接触一定可实现力封闭抓取[11]。因此本文抓取规划方法同样应用于四指夹持器的抓取规划中,同样在Cornell抓取数据集上进行实验,其典型结果如图18所示。 图18 四指抓取规划结果 154个算例中计算成功率为88.96%,各类型规划成功和失败个数如表3所示。 表3 四指抓取规划成功率(不同种类) 分析规划结果发现,相较于二指手爪抓取,四指手爪的计算成功率较高,且对于如圆形、椭圆形等弧形物体,四指手爪的接触点分布均匀,可更好地抵抗外力。 针对复杂轮廓平面物体传统抓取规划方法计算时间长,以及深度学习方法需大量数据集的问题,本文提出了一种基于傅里叶描述子的平面物体表征与抓取规划方法。使用傅里叶描述子实现平面轮廓的统一表征,在此基础上采用凸包推进算法计算力-力矩空间中抓取凸包的最大内切球半径作为抓取性能指标。使用改进的粒子群算法实现了抓取规划,并在二指和四指手爪模型上进行了验证,计算成功率高。


2.3 基于边界推进算法的抓取性能指标计算






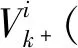
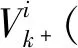
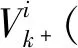



3 抓取规划方法与验证
3.1 基于改进粒子群的抓取规划方法





3.2 二指夹持器抓取规划



3.3 四指夹持器抓取规划


4 结束语
