基于扰动观测器的机载光电稳定平台自适应指数时变滑模控制

苗双全， 张宝泉， 王明超， 王新伟， 沈宇

(西安应用光学研究所， 陕西 西安 710065)

0 引言

机载光电稳瞄设备作为信息获取、融合、分析的重要环节，是夺取现代信息化战争胜利的关键组成部分。其中光电陀螺稳定平台，是惯性稳瞄设备的核心部件之一，能够隔离载体外部扰动，使得内部传感器在惯性空间下保持稳定，是机载光电稳瞄设备效能发挥的重要前提。目前光电陀螺稳定平台主要采用位置和速度双闭环比例积分微分(PID)控制方法，因其结构简单，设计方便，在机载光电稳瞄设备中得到了广泛应用。随着机载光电稳瞄技术的不断发展，传统的双闭环PID控制已经无法满足使用要求，广大工程技术人员迫切需要一种能够提高系统控制精度的控制方法。

辛林杰等提出引入前馈控制技术，与传统双闭环控制构成复合控制方法，降低了系统动态滞后误差，解决了传统PID控制中跟踪精度和系统稳定性之间的矛盾。黄辽宁在经典PID控制算法的基础上，在微分环节输出加上数字滤波器，可以有效避免微分项输出突变引起的跟踪系统不稳定，提高了光电跟踪仪的跟踪精度和稳定性。丁策等采用基于伪微分反馈的控制技术对系统的控制性能进行了研究，提出采用试凑法对伪微分反馈控制器进行参数整定，有效提高了系统对外部扰动力矩的抗干扰能力。侯宏录等针对控制环境和目标状态发生较大变化的情况采用模糊PID控制，减小了系统的过渡时间和超调量，同时保证了系统跟踪精度。秦树旺等设计了一种多种群遗传算法优化的模糊控制方法，该方法在经典双闭环反馈控制器的速度环之前并联一个积分环节，既加快了系统的反应速度，又减小了稳态误差，对系统阶跃响应性能具有一定改善。然而这些方法仍然具有鲁棒性不强、使用范围有限和控制器参数难以整定等缺点，在载机强振动环境、摩擦力矩和参数不确定性的影响下控制精度会大打折扣。中科院韩京清研究员提出的自抗扰技术，吸取了 PID 算法的优点，通过扩张状态观测器对外部总扰动进行实时估计和补偿，不需要精确的数学模型，只需利用误差反馈进行控制。但同时也具有一些缺点：针对快时变干扰的估计能力不足；对干扰估计的精度有限；需要选取的参数过多,参数整定复杂等。

滑模变结构控制作为一种特殊的非线性控制，其非线性表现为系统结构处于不固定状态，系统有目的地按照滑动模态预设的轨迹进行运作，实现滑模变结构控制。基于滑动模态控制理论，滑模变结构控制无需考虑控制对象的参数，并且在系统运行中不需要考虑扰动因素，所以使得变结构控制具备抗外界干扰性强、响应速度快、对参数变化不敏感、物理结构简单等优势。洪华杰等采用非线性微分信号获取方法，设计了滑模变结构控制器，与传统双闭环PID控制算法相比，能够同时实现系统无超调和快速响应的目的。王红红等提出了一种滑模自适应控制器，运用自适应原理对系统参数进行在线估计，同时提出一种改进的指数趋近律，可有效提高系统的响应速度。夏先齐等提出了一种基于永磁同步电机的新型积分滑模控制器，克服了传统滑模控制无法快速趋近和削弱抖振的矛盾，提高了航空光电平台的跟踪精度和指向精度。刘京提出了一种基于变增益趋近律的级联滑模控制方法，可以提高系统的动态响应性能和鲁棒性，进一步提高了光电系统的目标捕获和跟踪性能。但是滑模变结构的鲁棒性是以滑模高频抖振为代价的，外界干扰和参数不确定性的强弱影响了滑模高频抖振的剧烈程度，限制了滑模变结构控制的实际使用价值。

为了解决以上问题，本文提出了一种基于非线性扰动观测器的自适应指数时变滑模控制方法。非线性扰动观测器具有算法简单、易于工程实现等优点，可以对外界扰动和参数不确定性等因素进行实时估计，利用该估计值补偿聚合扰动对伺服系统控制精度的影响，削弱聚合扰动对滑模变结构控制造成的高频抖振。并采用新型自适应算法在线实时估计滑模切换增益，避免切换增益过大带来的滑模抖振问题。同时为了解决滑模控制切换增益过度自适应问题，采用指数时变滑模全局鲁棒控制器，使滑模运动减少了到达段过程，闭环系统始终沿滑模面运动最终收敛至平衡状态。

1 光电平台数学描述

机载光电稳瞄平台作为被控对象，其系统结构如图1所示。其中和分别为电机电枢电阻和电感，为反电动势系数，为力矩系数，为负载转动惯量，为功率放大系数，为控制电压，和分别为转动角速度和角位置，为外界扰动力矩，包括载机振动干扰力矩、摩擦力矩、线绕力矩和不平衡力矩等。

图1 伺服系统被控对象模型框图Fig.1 Block diagram of the controlled object of the servo system

根据被控对象结构，可以得到简化系统传递函数为

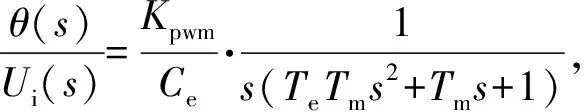
(1)

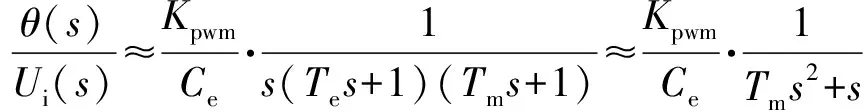
(2)

考虑外界扰动力矩的影响，光电稳定平台的动力学方程可以表示为

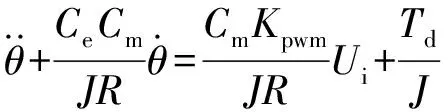
(3)

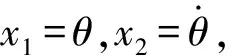
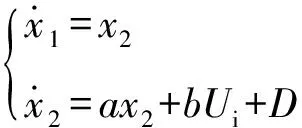
(4)

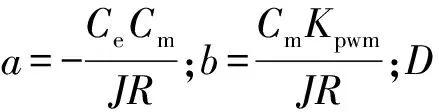
光电稳定平台的控制目标是：设计控制输入，使得当时间→∞时，→(为期望角位置)，且系统渐近收敛于平衡态。

2 控制器的设计

为了实现光电稳定平台的控制目标，本文采用基于非线性扰动观测器的自适应指数时变滑模控制策略，该方法利用非线性扰动观测器对聚合不确定性进行估计，该估计值可以抵消部分聚合不确定性，削弱聚合不确定性引起的滑模高频抖振，进一步提高系统控制精度。系统控制结构图如图2所示。

图2 光电稳定平台控制结构图Fig.2 Control diagram of the photoelectric stabilized platform

控制器可以表示为

=+

(5)

控制器的设计分为两步：第一步设计非线性扰动观测器，通过扰动观测器观测聚合不确定性，得到抵消聚合不确定性的控制输入；第二步设计自适应指数时变滑模控制器，用来实现光电稳定平台在残余聚合扰动影响下的期望角位置转动的全局鲁棒控制。

2.1 非线性扰动观测器的设计

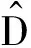
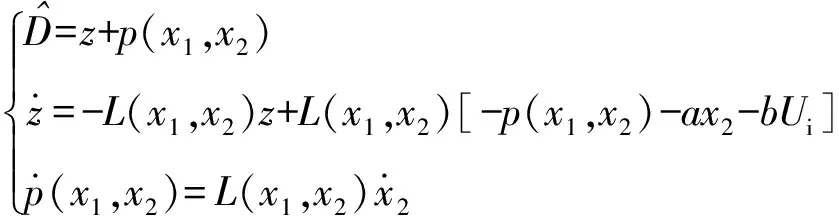
(6)

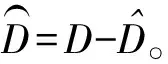
(7)

(8)

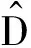
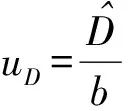
(9)

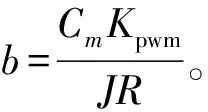
2.2 自适应指数时变滑模控制器的设计

因为扰动观测器观测聚合不确定性会存在残差，所以通过扰动观测器补偿之后的系统状态空间方程可以表示为

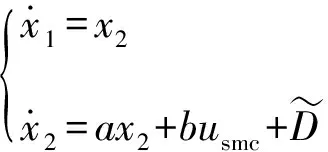
(10)

=+

(11)

式中：>0。采用文献[18]提出的指数趋近律，如(12)式所示。相比等速趋近律，可以通过减小切换增益和增大的方式在保证趋近速度的同时消弱滑模抖振的影响。

(12)

结合(10)式，滑模控制律可以设计为

(13)

式中：>0，>0，sgn(·)表示符号函数。

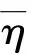
(14)

式中：>0。

定义李雅普诺夫函数为

(15)

现对李雅普诺夫函数沿闭环系统轨迹求导

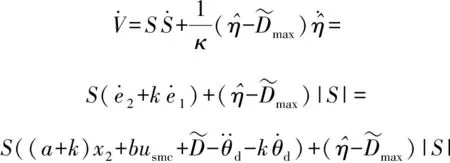
(16)

将滑模控制律(13)式和自适应律(14)式代入上式，可以得到

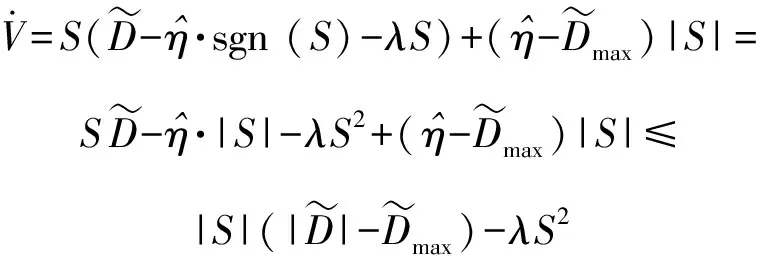
(17)

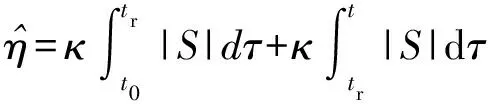
(18)

式中：表示闭环系统状态到达滑模面的时间。可以发现，切换增益自适应过程也分为两个过程，分别为到达段和滑模段。对于光电稳定平台大角度范围转动的情况下，系统初始状态距离滑模面较远，即|()|很大。因此，相比于聚合扰动，在系统机动的初始阶段时闭环系统的初始状态误差才是切换增益自适应过程的主导因素。可以发现：造成现有自适应滑模控制对切换增益的过度自适应的原因，在于将任何导致滑模面偏离的因素都考虑到切换增益的自适应过程当中，并未考虑闭环系统初始误差对自适应过程的影响。

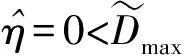
考虑指数时变滑模函数如下所示

=+-e-(-)

(19)

式中：=()+()，>0。对滑模函数求导

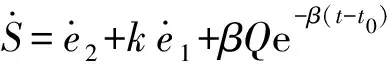
(20)

采用指数趋近律，则自适应指数时变滑模控制律可以设计为

(21)

为了证明在该控制律下闭环系统稳定性，现定义李雅普诺夫函数为

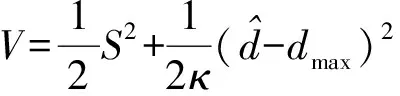
(22)

对其求导，可得

(23)

将滑模控制律(21)式代入上式，有

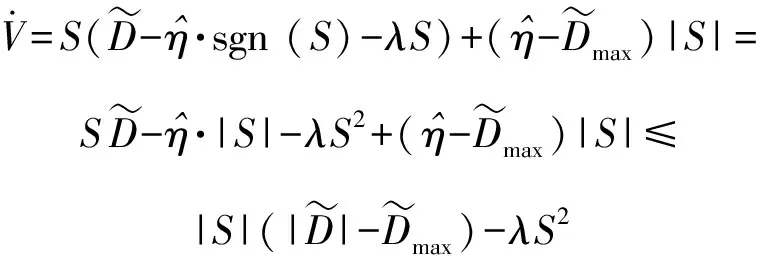
(24)

(25)

求解上述一阶微分方程，可得

(26)

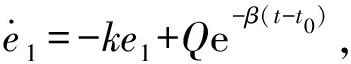
为了进一步减小因滑模切换带来的抖振，将自适应滑模控制律(21)式中的符号函数替换为饱和函数，这样做之后的系统则不再渐近稳定，而是渐近有界。同时，在实践工程当中，由于测量噪声和滑模有限频率的切换，滑模函数无法严格为零。此时根据(14)式所示的自适应律，可知切换增益会持续增大，并最终无界。为了解决这一参数漂移问题，可以利用文献[21]中的sigma修正法，从而获得有界的切换增益。则修正后的自适应指数时变滑模控制律可以写为

(27)

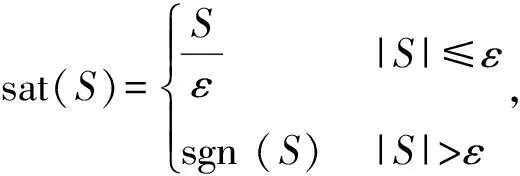
3 数值仿真和样机试验

为了验证本文提出方法的有效性，本节进行了数值仿真试验。某型光电稳定平台采用的直流力矩电机等效电枢电阻=8 Ω，电感=11 mH，反电动势系数和力矩系数为033，负载转动惯量=08 kg·m，PWM放大系数为25。外界扰动模型选择为15 Hz～2 000 Hz白噪声，并分别叠加80 Hz、160 Hz、180 Hz和240 Hz定频正弦扰动。负载转动惯量误差Δ=03sin()·。轴系转动摩擦采用文献[22]所述的Stribeck摩擦模型，摩擦力矩表达式为

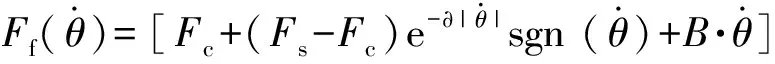
(28)

式中：库伦摩擦力矩=001 N·m；最大静摩擦力矩=003 N·m；粘滞摩擦系数=002；为经验常数，一般取值为3。

令光电稳定平台初始时刻=0，初始角位置()=1 rad，期望角位置为=0。

因此，应对各校区核算的流程和标准进行系统梳理，理顺校区间核算关系，进行协同管理，制订学习计划，编制培训资料，形成常态化学习机制和协同工作机制。通过定期组织各校区核算人员共同学习、解读政策制度，建立统一大核算微信交流平台，出台统一核算报销规范手册等措施，逐步实现尺度统一。

控制器设计中扰动观测器的观测增益=100，滑模函数中的=5，普通滑模切换增益=4，指数时变滑模函数的=52，趋近律中的=10，饱和函数边界层厚度=001，切换增益自适应律中的=5，=01。

为了说明本方法的有效性，现分别对(13)式所示的普通滑模控制器(SMC)、(27)式所示的自适应指数时变滑模控制器(AETVSMC)以及(9)式和(27)式所示的扰动观测器+自适应指数时变滑模控制器(DOB+AETVSMC)3种算法进行仿真，结果如图3～图6所示。

图3 角位置响应比较Fig.3 Comparison of the angle position response

图4 控制力矩曲线比较Fig.4 Comparison of the control torque curves

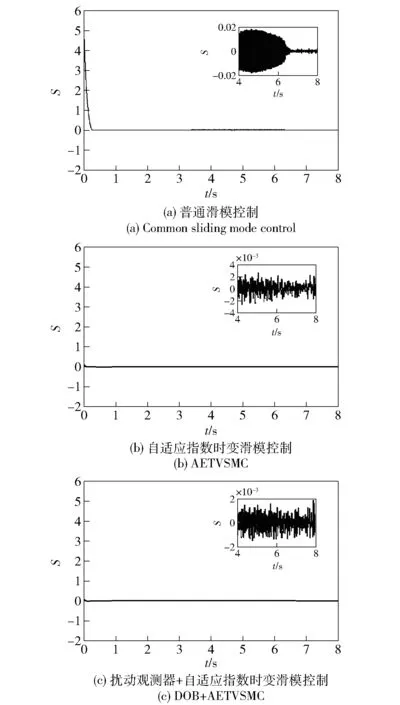
图5 滑模函数曲线比较Fig.5 Comparison of the sliding mode function curves

图6 自适应切换增益曲线比较Fig.6 Comparison of the adaptive switch gain curves

将普通SMC与AETVSMC这两种算法进行比较，光电稳定平台角位置响应时间基本都在1.5～2 s之间。普通SMC的稳态控制精度为0.06 mrad，角位置曲线粗细变化是因为转动惯量误差正弦变化引起的，AETVSMC的稳态控制精度为0.04 mrad，稳态控制精度得到了改善。普通SMC的控制力矩峰值为-42 N·m，而AETVSMC的控制力矩峰值为-20 N·m，控制力矩峰值更小，对于有输出力矩限制的执行机构更容易实现，且AETVSMC控制力矩的抖动更小，减小了对执行机构的机械磨损。普通SMC的滑模函数存在到达段，而AETVSMC的滑模函数一直为0，表明闭环系统一直处于滑模面上，具有全局鲁棒性。同时AETVSMC因为对切换增益的自适应调整，滑模抖振要小的多，表明AETVSMC对于减小滑模抖振具有很好的效果。AETVSMC的切换增益在自适应律的在线调整下峰值值为0.08，稳态值为0.007，相比普通SMC切换增益要小很多，避免了普通滑模切换增益过大而导致滑模高频抖振加剧问题。

将AETVSMC与DOB+AETVSMC这两种算法进行比较，DOB+AETVSMC继承了AETVSMC的全部优点。进一步可以发现，在相同的响应速度下，DOB+AETVSMC的控制精度为0.012 mrad，比AETVSMC控制精度提升了3倍以上。同时闭环系统状态始终在滑模面上，具有全局鲁棒性。在相同自适应律下，AETVSMC切换增益估计值峰值为0.08，稳态值为0.007，而DOB+AETVSMC的切换增益估计值峰值只有0.03左右，稳态值为0.004，相比AETVSMC切换增益要小很多，这是因为切换增益的估计值与聚合扰动的大小有关，扰动观测器补偿了部分聚合扰动对系统的影响，因此所需的切换增益就更小，减弱了滑模的高频抖振，进一步提升了系统的控制精度。3种控制方法的系统性能比较结果如表1所示。

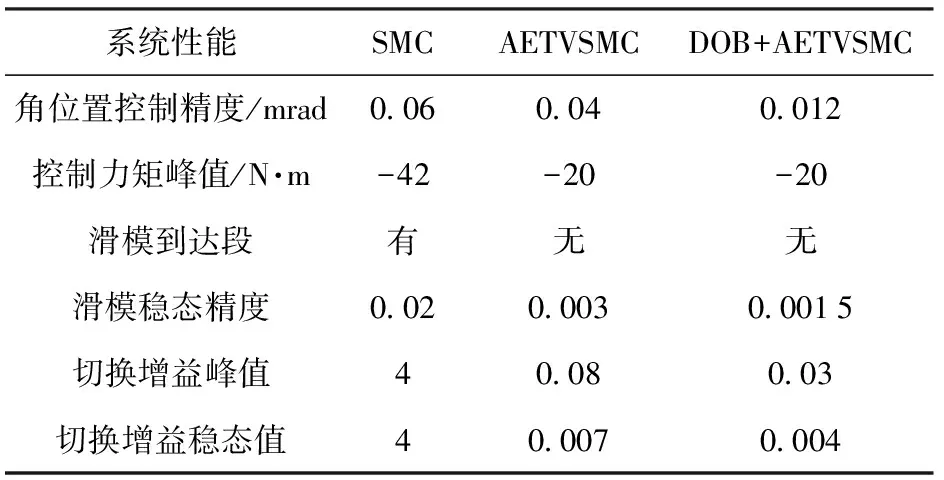
表1 系统控制性能比较

为了进一步验证本文所提方法的有效性，进行了样机验证。试验采用两轴两框架光电稳定平台，在小俯仰角的情况下对平台的方位角位置阶跃响应进行测试，样机测试环境示意图如图7所示。

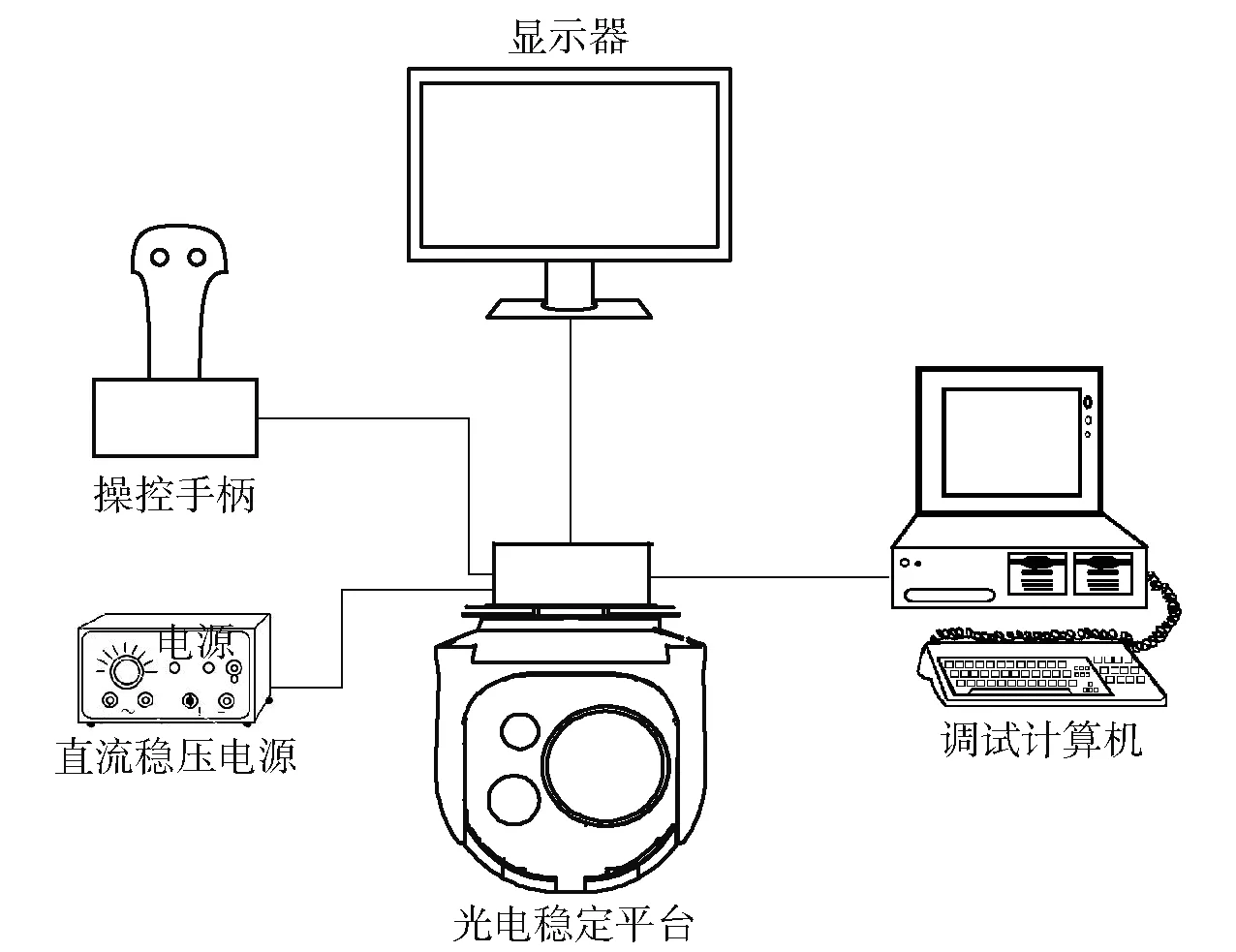
图7 样机测试环境示意图Fig.7 Prototype test setup

令光电稳定平台初始时刻角位置(0)=1 rad，期望角位置=0 rad。现采用传统双闭环PID控制(PID)、普通滑模控制(SMC)与扰动观测器+自适应指数时变滑模控制(DOB+AETVSMC)3种算法进行对比，试验结果如图8所示。

图8 角位置响应比较Fig.8 Comparison of the angle position response

从图8可以看出，为了满足响应速度要求，传统双闭环PID控制具有较大超调，而普通SMC与DOB+AETVSMC角位置响应曲线平稳，克服了传统双闭环PID控制具有较大超调的缺点。普通SMC的控制精度为0.08 mrad，而DOB+AETVSMC的控制精度可以达到0.03 mrad左右，表明DOB+AETVSMC具有更高的控制精度。

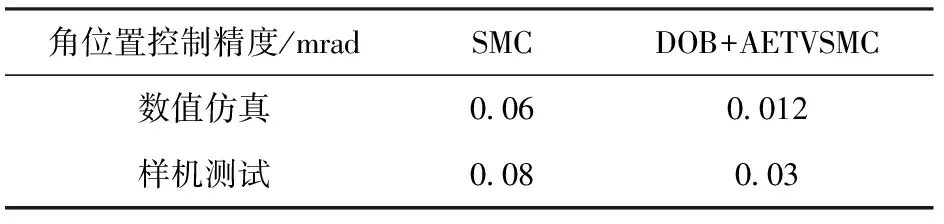
表2 数值仿真与样机测试中角位置控制精度比较

对光电稳定平台进行跟踪响应测试。系统跟踪响应曲线如图9所示。其中期望输入指令为正弦波，幅值为20°，周期为2π，如图9中红色虚线所示。

图9 跟踪角位置响应Fig.9 Response of track angle position

从图9中可以看出，DOB+AETVSMC控制下光电稳定平台可以实现对期望正弦指令的完全跟踪，且系统的稳态跟踪误差在0.1°以内，如图10所示，满足系统实际使用要求。验证了该方法的有效性。

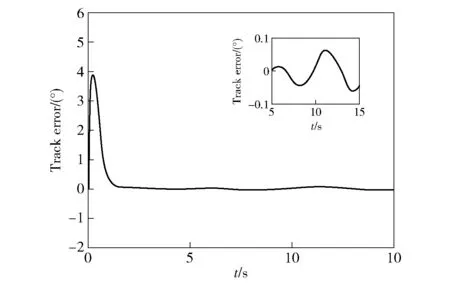
图10 跟踪误差曲线Fig.10 Track error curve

4 结论

本文针对存在外界扰动和参数不确定性的光电稳定平台高精度控制问题，提出了一种基于非线性扰动观测器的自适应指数时变滑模控制方法。从理论分析与数值仿真结果可以看出，非线性扰动观测器可以有效补偿聚合扰动对系统控制精度的影响。结合滑模变结构控制的鲁棒性，进一步降低了未观测到的残余聚合扰动对系统的干扰。通过自适应技术对滑模切换增益进行在线调节，解决了滑模切换增益对聚合扰动上界信息的依赖，同时采用指数时变滑模函数的设计，消除了闭环系统的滑模到达段过程，使闭环控制系统具有全局鲁棒性，并避免了切换增益过度自适应的问题，进一步提高了系统的控制精度。数值仿真和样机测试验证了所提方法的有效性。同时发现在实际的工程当中，执行机构的实际输出力矩都是有限的，本文在进行控制器设计时并没有考虑控制力矩饱和受限对系统控制性能的影响。因此，输入饱和问题将是进一步的研究方向。

[1] 丛爽, 邓科, 尚伟伟，等. 陀螺稳定平台建模分析[J]. 科技导报, 2011, 29(9): 42-47.

CONG S, DENG K, SHANG W W, et al. Modeling analysis on the gyro stabilized[J]. Science & Technology Review, 2011, 29(9): 42-47. (in Chinese)

[2] 吕宏宇, 金刚石, 高旭辉. 两轴四框架机载光电平台稳定原理分析[J]. 激光与红外, 2015, 45(2):194-198.

LÜ H Y, JIN G S, GAO X H. Stabilization analysis of airborne electro-optical platform with two-axis and four-gimbal[J]. Laser & Infrared, 2015, 45(2): 194-198. (in Chinese)

[3] 孙名佳. 滑模变结构与自适应控制在伺服控制系统中的应用[D]. 哈尔滨: 哈尔滨工业大学, 2009.

SUN M J. The application of SMC and MRAC in servo control system[D]. Harbin: Harbin Institute of Technology, 2009. (in Chinese)

[4] 辛林杰, 魏志强, 李斌. 前馈控制在光电跟踪系统中的应用研究[J]. 电视技术, 2020, 44(4): 27-31.

XIN L J, WEI Z Q, LI B. Research and application of feedforward control in photoelectric tracking system[J]. Video Engineering, 2020, 44(4): 27-31. (in Chinese)

[5] 黄辽宁. 改进PID算法在光电跟踪仪中的应用研究[J]. 自动化技术与应用, 2019, 38(8): 1-4.

HUANG L N. Application of improved PID algorithm in photoelectric tracker[J]. Techniques of Automation & Applications, 2019, 38(8): 1-4. (in Chinese)

[6] 丁策, 戴明, 李嘉全, 等. 机载光电陀螺稳定平台的伪微分反馈控制[J]. 光电工程, 2012, 39(10): 128-134.

DING C, DAI M, LI J Q, et al. The PDF control of airborne photoelectric gyro stabilized platform[J]. Opto-Electronic Engineering, 2012, 39(10): 128-134. (in Chinese)

[7] 侯宏录, 周德云, 王伟, 等. 模糊PID控制在光电跟踪控制系统中的应用[J]. 光电工程, 2006, 33(5): 12-16.

HOU H L, ZHOU D Y, WANG W, et al. Application of fuzzy-PID control in system of photo-electric tracking[J]. Opto-Electronic Engineering, 2006, 33(5): 12-16. (in Chinese)

[8] 秦树旺, 毛耀, 包启亮. 光电跟踪系统的模糊Ⅱ型控制技术研究[J]. 激光技术, 2021, 45(2): 147-154.

QIN S W, MAO Y, BAO Q L. Research on fuzzy Ⅱ-order control method of photoelectric servo tracking systems[J]. Laser Technology, 2021, 45(2): 147-154. (in Chinese)

[9] 李家豪, 孙洪飞. 自抗扰控制技术的改进和应用[J]. 厦门大学学报(自然科学版), 2018, 57(5): 695-701.

LI J H, SUN H F. Improvement and application of active disturbance rejection control[J]. Journal of Xiamen University (Natural Science), 2018, 57(5): 695-701. (in Chinese)

[10] UTKIN V. Varible structure systems with sliding modes[J]. IEEE Transactions on Automatic Control, 1977, 22(2): 212-222.

[11] 高为炳. 变结构控制理论基础[M]. 北京: 科学出版社, 1990.

GAO W B. Theory foundation of variable structure control[M]. Beijing: Science Press, 1990. (in Chinese)

[12] 穆效江, 陈阳舟. 滑模变结构控制理论研究综述[J]. 控制工程, 2007, 14(增刊2): 1-5.

MU X J, CHEN Y Z. Overview of sliding mode variable structure control[J]. Control Engineering of China, 2007, 14(S2): 1-5. (in Chinese)

[13] 任亚婧, 段友莲, 胡兵. 光电稳定平台的变结构控制策略研究[J]. 舰船科学技术, 2020, 42(8): 217-219.

REN Y J, DUAN Y L, HU B. Research on variable structure control strategy for photoelectric stability platform[J]. Ship Science and Technology, 2020, 42(8): 217-219. (in Chinese)

[14] 洪华杰, 贠平平, 王学宁, 等. 光电稳定滑模变结构控制系统的设计与仿真[J]. 计算机仿真, 2010, 27(7): 130-133,221.

HONG H J, YUN P P, WANG X N, et al. Design and simulation of variable structure control system based on sliding mode for photoelectric stabilized platform[J]. Computer Simulation, 2010, 27(7): 130-133,221. (in Chinese)

[15] 王红红, 陈方斌, 江涛, 等. 不确定非线性光电伺服系统滑模自适应控制[J]. 应用光学, 2009, 30(2): 242-245.

WANG H H, CHEN F B, JIANG T, et al. Adaptive SMC for nonlinear optoelectronic servo system with uncertainty[J]. Journal of Applied Optics, 2009, 30(2): 242-245. (in Chinese)

[16] 夏先齐, 张葆, 李贤涛, 等. 基于扩张状态观测器的永磁同步电机低速滑模控制[J]. 光学精密工程, 2019, 27(12): 2628-2638.

XIA X Q, ZHANG B, LI X T, et al. Low speed sliding mode control of permanent magnet synchronous motor based on extended state observer[J]. Optics and Precision Engineering, 2019, 27(12): 2628-2638. (in Chinese)

[17] 刘京, 邓永停, 李洪文. 基于级联滑模控制的高精度光电跟踪与捕获[J]. 光学精密工程, 2020, 28(2): 350-362.

LIU J, DENG Y T, LI H W. High-precision photoelectronic acquisition and tracking based on cascade sliding mode control[J]. Optics and Precision Engineering, 2020, 28(2): 350-362. (in Chinese)

[18] 高为炳. 变结构控制的理论及设计方法[M]. 北京: 科学出版社, 1996.

GAO W B. Theory and design method of variable structure control[M]. Beijing: Science Press, 1996. (in Chinese)

[19] 苗双全, 丛炳龙, 刘向东. 基于输入成形的挠性航天器自适应滑模控制[J]. 航空学报, 2013, 34(8): 1906-1914.

MIAO S Q, CONG B L, LIU X D. Adaptive sliding mode control of flexible spacecraft on input shaping[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1906-1914. (in Chinese)

[20] 丛炳龙, 刘向东, 陈振. 刚体航天器姿态跟踪系统的自适应积分滑模控制[J]. 航空学报, 2013, 34(3): 620-628.

CONG B L, LIU X D, CHEN Z. Adaptive integral sliding mode control for rigid spacecraft attitude tracking[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(3): 620-628. (in Chinese)

[21] WHEELER G, SU C Y, STEPANENKO Y. A sliding mode controller with improved adaption laws for the upper bounds on the norm of uncertainties[J]. Automatica, 1998, 34(12): 1657-1661.

[22] 韩小康, 董浩, 王明, 等. 光电稳定平台中Stribeck摩擦力矩的补偿方法[J]. 火力与指挥控制, 2019, 44(10): 123-126.

HAN X K, DONG H, WANG M, et al. The research on stribeck friction torque compensation method in photoelectric stabilized platform[J]. Fire Control & Command Control, 2019, 44(10): 123-126. (in Chinese)