煤储层渗透率测试、模拟与预测研究进展

2022-08-02傅雪海张宝鑫

煤炭学报 2022年6期

傅雪海，齐琦，程鸣，张宝鑫

(1.中国矿业大学煤层气资源与成藏过程教育部重点实验室，江苏徐州 221116；2.国家煤层气产品质量监督检验中心(山西)，山西晋城 048000)

渗透率是表征煤层气可采性的关键参数之一，直接影响到煤层气采收率及可采资源量。煤层气产出经历三级流动阶段，气井排水压降至临界解吸压力以后，煤层气从煤基质孔隙解吸，浓度差的存在驱使气体逐渐向显微裂隙扩散，再在流体势的作用下流向宏观裂隙，运移至井筒产出。整个流动过程与煤储层渗透率密切相关。

煤储层渗透率主要通过现场原位储层测试(下文简称试井渗透率)和样品实验室测试(下文简称实验渗透率)及数值模拟和预测获得。我国绝大多数煤储层呈现为欠压、低渗特征，钻杆测试、水罐测试及段塞测试均难获得试井渗透率，注入/压降测试也不完全适用我国大多数气饱和储层，且测试成本高。由于煤储层裂隙发育的非均质性，同一煤层气区块不同位置获得的试井渗透率相差几个数量级，少量试井结果难以反映整体煤储层的状态。不同测试仪器、测试方法、样品尺寸、围压、流压、温度及测试介质条件下获得的实验渗透率也没有可比性。煤储层渗透率测值的不准确性是导致我国部分煤层气井累计产气量大于由试井渗透率计算的单井煤储层产气量的原因之一。

煤储层渗透率受多因素影响，如天然裂隙、煤体结构、煤岩、煤质特征及地质构造、应力状态、有效埋藏深度(温度、压力)、煤化程度、构造演化历史、水文地质条件等。国内外学者对影响因素的相关研究取得了一系列成果。笔者侧重分析煤储层渗透率测试、模拟及预测方法的可靠性及适应性。

1 测试

渗透率测试方法有2种：一是在现场对原位煤储层进行的试井法；二是在实验室对煤柱样进行地层温度条件下的流量测试法。

1.1 试井法

常用的试井法有钻杆测试(也叫DST测试)、注入/压降测试、段塞测试、水罐测试和干扰测试等。不同的测试方法有其优缺点及适用范围(表1)，地质条件及流体状态影响了测试的准确性。煤储层试井方法的选择除受井况制约外，还受完井类型、储层压力、渗透率大小及储层流体类型的影响。

表1 煤储层渗透率常用的试井方法评述

DST测试在确定煤储层基本参数方面具有独特优势。对勘探井而言，最好的测试时机为钻井过程中进行裸眼DST测试，即打开煤储层后立即进行测试，此时储层损害最轻且所有可产气层均可进行测试，便于对储层参数做出准确评价。但对于低压低渗储层，由于产量低、开井时间短等因素的影响，常常达不到径向流，导致试井资料不能解释，测试失败，姚艳芳等在龙1井第1次DST测试即此原因导致不能计算储层参数。

注入/压降测试获得的煤储层渗透率参数较可靠，但对于储层压力低、渗透率小的区块，压力传播速度较慢，可考虑适当延长测试时间提高测试的可靠性。曹运兴等通过在潞安矿区30余口煤层气井的延时试井测试，验证了注入时间为8～12 h、关井时间为注入时间7～11倍时测试结果的可靠性。

对未进行措施改造的套管方式完井的井，测试前通常需要进行疏通处理或实施微型改造措施，以便提高井底附近被污染的裂隙与储层的连通性，提高测试成功率。这些小规模措施改造产生的裂隙较短，在较短的测试时间内就能达到拟径向流；对于措施改造后的套管方式完井的井，若无措施改造前的测试资料，则需通过延长测试时间或增大注入压力等可控因素，获得更可靠的煤储层参数。此外，应采用井下关井工具，减小井筒储集的影响，提高测试成功率。对措施井尽量不采用段塞测试，因为段塞测试的探测半径小，解释结果不惟一。

综合以上研究，试井测试方法选择的关键因素是煤储层渗透率、煤储层压力条件、煤储层产出流体类型及产出流体能否到达地面(表2)。注入流体的选取不能改变原始地下流体，即对水饱和的煤储层绝对不能采用注气测试，而对存在大量游离气的井一般不采用注水测试。对于压力梯度大、渗透率高的煤储层，如果产出流体能够到达地面，可选择DST测试、压降/压恢测试或注入/压降测试；如果产出流体无法到达地面，则仅有注入/压降测试较适用。对于压力梯度小、渗透率高的煤储层，可选段塞测试或水罐测试，而对于储层条件较差，压力梯度小、渗透率低的煤储层，选择注入/压降试井测试，通过合理延长测试时间，也能够获取可靠的煤储层参数。

表2 煤储层渗透率试井方法对比[52-55]

我国煤储层绝大多数为低压、低渗储层，在多数煤层气勘探开发区内，储层流体不能自动产出到地面，这导致DST测试、水罐测试及段塞测试不适用，或者难以在保证成功率的前提下得到准确的储层参数，只有注入/压降测试，适用我国的煤储层特征且能够可靠地获得储层参数，目前广泛应用于我国煤储层参数测试和评价，并形成了煤层气行业国家标准。

此外，煤层气井生产数据历史拟合得到的煤储层渗透率大于注入/压降试井渗透率，通过历史拟合生产井的水、气产量及压力等排采数据，可以准确地认识煤储层渗透率参数。当拥有煤层气生产数据时，该方法所确定的渗透率较各种试井方法更准确，能够代表煤储层的真实渗透率。

1.2 流量测试法

依据不同测试原理，可将实验室渗透率测定方法分为2类：稳态法及非稳态法，不同方法的差别主要体现在测试原理(表3)、样品尺寸、质量、测试环境、精度等方面(表4)。稳态法包括恒压法、恒流法等，非稳态法主要为瞬态压力脉冲法。

表3 实验室渗透率测试方法示意、初始边界条件及原理

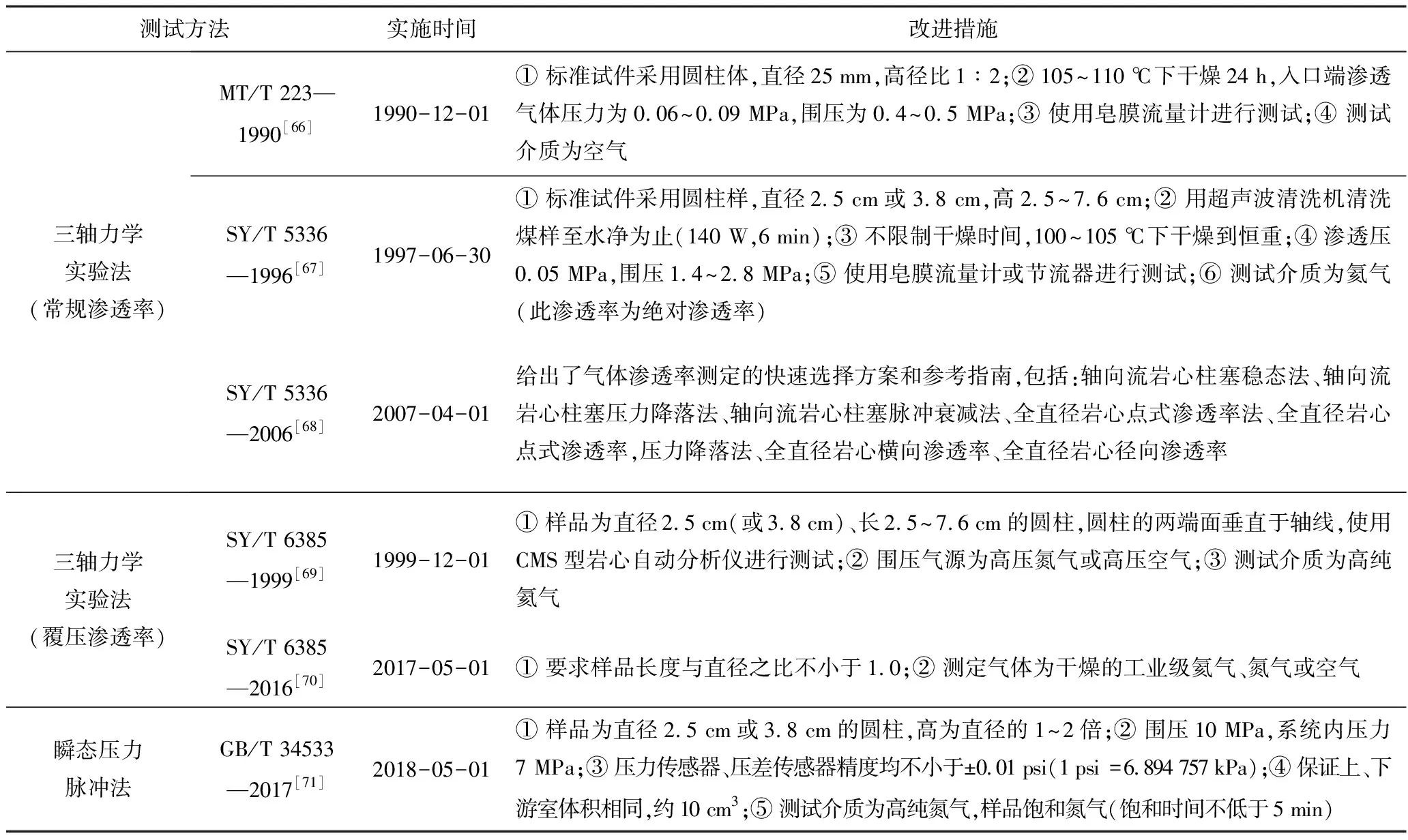
表4 煤样渗透率实验室测试方法演化

对于实验室渗透率测试来说，稳态法对高渗样品较为适用，对于渗透率较低的煤样，稳态法测试需要等待流体完全穿过测试样品，测试效率较低，且测试过程易受温度压力影响，误差较大。非稳态法规避煤样出口流速难以精准测量的难题，仅需记录脉冲压力由上游逐渐传到下游过程中两容器间的压差，测试效率较高，且可保证低渗煤样的测试精度。渗透率具有应力敏感性，加围压煤样渗透率降低，去围压后渗透率仅能部分恢复，高围压下所测煤样渗透率比低围压下低1～2个数量级。

2 模拟

模拟是指通过工程建模及数值计算等方法达到对工程问题和物理问题研究的目的。在模拟煤储层渗透率时，为突出裂隙的影响，通常采用理想化模型，如球形模型、毛细管模型、火柴棒模型和立方体模型(图1)。现阶段多使用火柴棒模型。

图1 煤基质规则化模型

模型的边界条件同样也是理想化的对象。假设在煤层气开采过程中煤储层垂直方向发生位移，边界条件可以假定为具有恒定垂直外应力的单轴应变条件模型(图2)；假设煤储层垂直与水平方向均未发生位移，边界条件可以假定为恒定体积条件模型；在实验室中，总是在三轴应力条件下测试煤的渗透率，即三轴应力条件模型。MASSAROTTO等认为恒定体积条件更适合煤储层。

图2 渗透率模型边界条件

2.1 单轴应变条件模型

1987年，GRAY在单轴应变条件下量化了基质收缩对裂隙渗透率的影响，他基于火柴棒模型，提出了考虑基质收缩及有效应力的渗透率模型(下文简称GRAY模型)。

(1)

式中，为入口压力，MPa；为出口压力，MPa；为黏度，Pa·s。

该模型存在的最大问题是认为基质收缩与等效吸附压力之间存在定量比例关系(表5)，而在煤储层天然裂隙中，渗透率对应力或孔隙压力的变化(即有效应力变化)很敏感。煤层气开采一方面导致煤储层压力下降，有效应力增加导致裂隙压缩，渗透率下降；另一方面煤层气解吸会使煤基质收缩，裂隙张开，渗透率增加。裂隙压缩负效应和基质收缩正效应对渗透率的耦合影响使得煤储层渗透率的理论模拟变为一个复杂的非线性问题。

表5 单轴应变条件模型演化分析

P-M模型由PALMER和MANSOORI于1996年提出，其描述方程适用于单轴应变条件下的煤储层，并将孔隙压力下降导致的有效应力效应和基质收缩效应结合在一个方程中。更重要的是基质收缩不再作为平均值，而是作为储层压力的函数并入模型中。

(2)

式中，为煤储层初始渗透率，10m；为轴向模量，MPa；为煤储层原始孔隙度，%；为煤储层压力，MPa；为煤储层初始压力，MPa；为孔隙体积模量，MPa；为朗格缪尔理论最大应变量，即无限压力下的渐进值；为朗格缪尔系数，MPa。

P-M模型是目前应用较为广泛的煤储层渗透率模型，是煤层气渗透率理论推导的基础。该理论的局限性主要是煤储层孔隙度变化必须很小，当孔隙度变化小于30%时，该理论较为准确，孔隙度变化超过30%时，模型的预测结果仍具有趋势性预测效果。此外，P-M模型基于的理想化假设：煤样处在单轴应变条件下且垂向应力恒定，其合理性有待商榷。因为煤层气开发主气流通常平行于煤储层，而不是垂直于煤储层，无法用只能提供单一轴向应力的常规岩心渗透率试验装置进行建模。

S-D模型由SHI和DURUCAN于2004年提出，为单轴应变条件下与孔隙压力相关的裂隙渗透率模型。模型中煤储层裂隙渗透率的变化受水平有效应力控制，将煤基质理想化为具有规则火柴棒几何形状，单轴应变条件下水平有效应力变化表示为孔隙压力降低的函数，其中包括对渗透率具有竞争性影响的裂隙压缩效应和基质收缩效应。

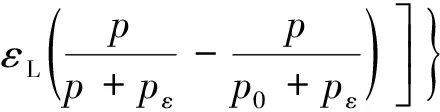
(3)

式中，为裂隙压缩系数，MPa；为泊松比；为弹性模量，MPa；为朗格缪尔型矩阵收缩常数。

S-D模型形式上与GRAY模型类似，均认为在流体压力下降过程中，裂隙渗透率的变化受主要有效水平应力控制。2个模型的最大区别为：S-D模型认为基质体积收缩与解吸气体的体积成正比，GRAY模型则认为基质体积收缩与等效吸附压力的降低成正比。SHI和DURUCAN在美国圣胡安盆地对该模型进行现场验证，模拟得到3口井在煤层气生产过程中绝对渗透率的增加量，发现其与P-M模型得到的渗透率非常一致，证明S-D模型至少能够定性预测较低压降下渗透率的增长趋势。

C-B模型是由CUI和BUSTIN于2005年基于线性非等温吸附模型提出的与应力相关渗透率模型，C-B模型假设气体吸附诱导的体积应变与气体吸附质的体积近似成正比，将煤储层因煤层气吸附效应导致的变形理想化为弹性多孔介质的温度变化效应：

(4)

该模型假设煤基质和煤裂隙中的压力始终相同，忽略了煤裂隙和煤基质之间可能存在的不同压力。

2.2 恒定体积条件模型

2009年，MASSAROTTO等认为煤储层实际上处于恒定体积条件，并指出随着时间的推移，储层的基本恒定体积(原始体积的99.72%～99.95%)是由储层上覆盖层的弯曲强度和拉伸强度保持的。2011年，MA等在恒定体积假设条件下，利用火柴棒模型提出了一种基于煤基质、固体颗粒和孔隙之间体积平衡的煤渗透率模拟方程(下文简称MA模型)。

恒定体积条件下，储层可以视为一个整体，包括2个组成部分：基质/颗粒体积和孔隙体积。由于该理论假设体积变化为0，所以煤基质尺寸的减小与裂隙孔径尺寸的增加相等。

(5)

MA模型的方程式虽然复杂，但所需的弹性模量()、泊松比()和收缩参数(和)均易测得，计算结果没有不确定性，是该模型的优点之一。此外，MA模型的渗透率模拟数据与历史匹配数据、P-M模型数据和S-D模型数据均拟合较好(图3，4)，准确度较高。

图3 MA模型、历史匹配和P-M模型渗透率增量对比[72]

图4 MA模型、历史匹配和S-D模型渗透率增量对比[72]

2.3 三轴应力条件模型

周军平等认为单独考察某个因素对煤岩渗透率的影响不够全面，他们综合考虑孔隙压力、有效应力和煤岩体基质收缩的共同作用建立了煤层气储层渗透率的一般性模型(下文简称ZHOU模型)。

ZHOU模型假设煤岩体各向同性，并且基于多孔弹性介质理论，将基质收缩效应等效于热收缩效应，理想化假设解/吸附效应只引发体积应变且引发的应变在3个主应力方向大小相等，同时考虑了煤颗粒的可压缩性。

(6)

式中，为正有效应力系数(0≤≤1)；为煤颗粒压缩率；为煤样达到最大应变量的一半时的压力；为初始压力为时的煤储层孔隙度。

ZHOU模型表明有效应力效应与解吸效应引起的体积应变互相影响，共同控制着渗透率大小，且影响效应相反。

CONNELL利用多孔介质和三轴应力假设提出了一种新的煤储层流动与地质力学耦合渗透率模型(下文简称CONNELL模型)。CONNELL模型将吸附应变划分为体积应变、孔隙应变和基质应变，将煤渗透性的变化视为有效应力的函数，假设各向同性吸附诱导应变、单轴应变条件和恒定的垂直应力。在该模型中，有效水平应力的变化是垂直应力、水平应变、水平吸附应变和孔隙压力变化综合作用的结果。CONNELL模型有2种形式：立方模型(形式类似于P-M模型，式(7))和指数模型(形式类似于S-D模型，式(8))。

(7)

=exp{-3[(-)+(-)]}

(8)

式中，为基准状态下的裂隙孔隙度；为孔隙围压，Pa；为参考状态下的孔隙压力，Pa；为吸附诱导的岩石体积应变；为吸附引起的基体体积应变；为吸附诱导的孔隙体积应变。

在2.0，4.0，6.0 MPa孔隙压力下，将计算的渗透率与实测渗透率进行比较，发现指数型和立方型模型模拟值与等效测量值均一致。但在孔隙压力较低时，模型的预测值高于测量值，在孔隙压力为2.0 MPa时，模型的预测值约高20%。

ROBERTSON和CHRISTIANSEN利用立方体模型和三轴应力假设，提出了煤和其他裂隙吸附弹性介质的渗透率模型(下文简称R-C模型)。以立方几何模型代替火柴棒模型，假设裂隙宽度的变化是由裂隙压缩性、机械弹性和吸附诱导应变引起的，将这3种效应相加，估算渗透率随储层压力的变化。

(9)

式中，为速度，cm/s；为无约束样品在无限孔隙压力下的线性应变；p为初始孔隙压力；为吸附诱导应变等于最大应变一半时的朗缪尔压力，6.895 kPa。

R-C模型适用于可变孔隙压力和恒定上覆压力。模型的敏感性分析表明，与泊松比和杨氏模量相比，孔隙度、吸附诱导应变和裂隙压缩性对渗透率的影响更为显著。ROBERTSON和CHRISTIANSEN将该模型的性能与P-M模型和S-D模型进行了比较，认为2个模型都夸大了吸附诱导应变对甲烷和氮气渗透率的影响。

2.4 模型对比

假设模型为恒定体积条件，则所有的煤基质吸附变形都会体现为煤样渗透性的变化，假设模型在具有恒定垂直外部应力的单轴应变条件下，则几乎所有的水平膨胀变形都会导致渗透率的变化。多数实验都是在保持外部应力不变的情况下进行的，此时外部边界可向水平和垂直扩展。

在现有的渗透率模型中，如S-D和P-M模型渗透率关系中使用的体积吸附应变，是通过假设孔隙和体积吸附应变等效实现的。但通过理论论证和模型对实验数据的应用表明，这些吸附应变可能不相等。ROBERTSON和CHRISTIANSEN发现，在单轴应变条件下开发的P-M和S-D模型无法与通过保持外部应力不变获得的渗透率数据良好匹配，煤裂隙和基质间存在相互作用，这一影响因素被忽略。

边界条件对渗透率模型非常重要。在定容条件下建立的模型，与基于单轴应变条件建立的模型有明显不同。根据MASSAROTTO等研究成果，尚未观察到因煤中产出甲烷而发生的沉降参考文献，目前尚无证据表明恒定体积条件是合理的，尽管单轴应变条件是目前最常用的模型基础，但没有任何支持其合理性的证据。因此，单轴应变条件和恒定体积条件之间的争议依旧存在，需要进一步研究，以最终确定哪一种情况适用于煤层气渗透率模拟。

目前实验室三轴渗透率测试和实验室岩心测试很难复制S-D模型和P-M模型。为了简化地质力学过程，设定了理想化的单轴应变和恒定垂直应力。因而三轴应力边界条件更具有适用性，并且可通过替换特定的边界条件，三轴应力模型可以转换为具有恒定体积、单轴应变或其他边界条件的模型。

恒定体积条件、单轴应变条件或三轴应力条件都只是煤储层的假定边界条件。影响煤储层渗透率的因素多且复杂，不仅仅与其所处的力学边界条件有关，后续模拟模型可考虑对煤储层渗透率进行多物理场、多因素耦合动态研究。

3 预测

煤储层渗透率预测的基本思路是利用已有数据，建立渗透率与其影响参数之间的定量关系(表6)，实现对未知区域渗透率的预测。煤储层渗透率的内在影响因素包括：裂隙、孔隙和煤体结构等；外在影响因素包括：原地应力、有效应力等。大量学者基于渗透率与上述单一影响因素间关系，建立了适用不同地区的渗透率定量预测模型。同时，部分学者利用现代计算机技术、人工智能手段对煤储层进行考虑多因素的渗透率综合预测。

表6 渗透率影响因素与定量预测

3.1 单一主控因素预测

..裂隙

煤储层是由煤裂隙和煤基质组成的双孔隙介质，其渗透率大小与裂隙系统密切相关。HOBBS研究表明渗透率与裂隙系统参数存在如下关系：

(10)

其中，为基质渗透率；为煤裂隙壁距；为煤裂隙间距；为裂隙面与水平面夹角。煤储层基质渗透率较小，基本可以忽略不计，由式(10)可知煤储层的裂隙壁距与间距对渗透率起控制作用，可根据裂隙的发育情况对储层渗透率进行预测。

笔者对采自沁水盆地中—南部5个矿井的块煤样进行裂隙与渗透率耦合分析表明：大裂隙发育的煤样渗透率最高(晋城成庄矿、高平望云矿)；小裂隙较发育的煤样渗透率中等(沁源沁新矿)；裂隙不发育的煤样渗透率最低(潞安常村矿、五阳矿煤样)。随着裂隙面密度的增加，模拟渗透率指数增加：

=0029 2exp(0009 6)

(11)

其中，为裂隙面密度模拟渗透率，10m；为裂隙面密度，条/m。当裂隙面密度大于128条/m时，煤储层渗透率大于0.1×10m。

笔者结合LEVINE提出的公式，结合渗透率裂隙二阶张量公式，建立了渗透率与裂隙宽度之间的数学模型，通过压缩实验，结合浅部煤裂隙对该区深部煤储层渗透率进行了预测。

(12)

(13)

其中，为有效渗透率；,,分别为割理倾角、倾向、走向；为裂隙粗糙系数；为裂隙组组号；为裂隙组总数。结果表明随埋深增加裂隙宽度指数降低，煤储层渗透率随之指数降低，煤储层埋深大于1 000 m，其渗透率普遍小于0.1×10m。

MCKEE假定颗粒不可压缩，假设Carmen-Kozeny方程有效，孔隙度的变化与总有效应力的变化成反比，推导了煤渗透率、孔隙度和与有效应力、裂隙宽度等参数间的函数表达式，表明渗透率大小与裂隙宽度的3次方成正比(相关系数大于0.95)。因此，在煤储层其他赋存状态相差不大时，天然裂隙系统是否发育直接决定着渗透率的大小，裂隙系统越发育，越有利于形成高渗透率煤储层。

..煤体结构

煤体结构是煤储层在构造应力作用下的结果，煤体构造变形程度的反映。

吕闰生等按《防治煤与瓦斯突出规定》将采自焦作煤田的煤样划分为5类(Ⅰ～Ⅴ)。使用煤坚固性系数作为煤体结构分类的指标建立了渗透率与的定量函数表达式为

=3392 6exp[-25770 2(-075)]+0010 2

(14)

该模型相关系数为0.78，拟合性较好。当煤体结构由简单(Ⅰ类)变复杂(Ⅴ类)，渗透率先增大后减小呈指数非线性称变化。Ⅰ类煤、Ⅲ～Ⅴ类煤渗透率相对较低，Ⅱ类及Ⅱ～Ⅲ类过渡煤体渗透率最高。

笔者对两淮煤田各矿井煤体结构观测和钻孔煤层测井曲线解释，将煤体结构划分为原生结构-碎裂煤(Ⅰ类)、碎斑煤(Ⅱ类)和糜棱煤(Ⅲ类)3种类型。通过聚类分析，结合煤储层试井渗透率，建立了煤储层渗透率与煤体结构间的定量函数：

=7642 8×10exp(-968)

(15)

式中，为煤储层中Ⅱ，Ⅲ类煤所占煤厚比值，%。

煤储层中Ⅱ类、Ⅲ类煤厚度占比大于50%，其渗透率低于0.1×10m；只有Ⅱ类、Ⅲ类煤占比小于20%时，煤储层渗透率才有可能达到1.0×10m以上。

..地应力

刘大锰等拟合表明沁水盆地郑庄区块试井渗透率随最小水平主应力、最大水平主应力、垂向主应力和有效应力的增大均呈负指数减小(图5)。

图5 沁水盆地南部郑庄区块渗透率与地应力拟合关系[90]

笔者基于煤样在储层条件下的三轴压缩力学实验，得到了不同水平应力下的力学参数，利用FLAC-3D软件模拟了山西沁水盆地中南部上主煤储层(山西组3号煤层)应力大小，结合18套煤储层试井渗透率成果，建立了应力-渗透率耦合数学模型：

=297883exp(-0238-0378+

0208+0543)

(16)

式中，为垂向主应力，MPa；为最大水平主应力，MPa；为最小水平主应力，MPa；为剪应力，MPa。

模型预测结果显示：煤储层渗透率呈椭圆形分布，盆地底部(埋深1 000 m以深)渗透率小于0.1×10m；盆地斜坡带(埋深600～1 000 m)渗透率在0.1×10～0.5×10m；盆地西缘和北部渗透率在0.5×10m左右；盆地东缘和南部渗透率大多在0.5×10～1.0×10m。

煤储层渗透率与埋深呈负相关，孟召平等对沁水盆地南部43口煤层气井试井渗透率的研究结果认为，煤储层渗透率随埋深变化的实质是地应力作用的结果。埋深在650 m以浅的煤储层，最小水平主应力小于12 MPa，此时储层渗透率平均值大于1.0×10m；在650～1 000 m煤储层，最小水平主应力为12～20 MPa，此时煤储层渗透率的平均值大于0.1×10m；在1 000～1 500 m煤储层，最小水平主应力大于20 MPa，煤储层渗透率平均值大于0.01×10m。具体来说，随埋深的增大，沁水盆地中、南部煤储层试井渗透率指数减小(图6)。

图6 渗透率与埋深关系曲线[105]

..构造曲率

构造曲率是表征线/面弯曲程度的量化参数，其大小可用于反映煤储层变形程度。通过构造曲率来评估裂隙发育情况，是最具代表性的高渗区地质预测法，该法认为在岩石力学性质相似的条件下，曲率越大，裂隙越发育，渗透性就越好，最大构造曲率地带即是高渗透区。

林然等采用构造曲率来预测渗透率，把樊庄区块划分为特高、高、中等、低4个曲率区，实现了该区块高渗区预测。赵争光等基于最大主曲率对海拉尔盆地呼和湖凹陷C煤层进行了的煤储层渗透性预测，构建了基于最大构造曲率、煤储层厚度和裂隙间距的煤储层渗透率数值预测模型。

(17)

黄波等也通过上述公式预测古交区块8号煤储层渗透率，预测结果表明：该区块煤储层渗透率介于0.002×10～0.650 ×10m，北部最高，东部最低；与试井、试验测试裂隙渗透率的结果较为吻合，证实了该方法预测的准确性。

需要指出的是，构造曲率过高会影响到煤体裂隙的张开，往往会促使煤体严重破碎的构造煤发育，导致煤储层渗透率极差，这也是该法近年来受到普遍质疑的原因。

上述煤储层渗透率均是与单一主控因素间的定量预测。但影响煤储层渗透率大小的内、外因素很多，在不同的赋存环境下，主导控制因素会有所变化。因此在进行渗透率预测时需要因地制宜地选择主控影响因素，效果最好应该是综合预测。

3.2 人工智能综合预测

现代计算机手段在煤储层渗透率预测方面得到了越来越多的应用。煤储层渗透率受多种影响因子综合影响，通过灰色关联技术，多层次模糊综合评价等方法，能够优选出关键影响因子，同时结合神经网络及支持向量回归机等方法，发挥非线性动力学系统的优势，使预测更为精准(表7)。

表7 煤储层渗透率人工智能综合预测方法

4 问题与展望

煤储层渗透率测试、模拟及预测已进行了大量的研究，并在试井测试和实验室测试等方面形成了标准。但由于煤储层孔裂隙发育、气体赋存、构造作用及应力分布的复杂性，煤储层渗透率在精确测试、精准模拟和精度预测方面还存在诸多问题。

(1)对试井方法而言，由于储层流体状态、煤储层非均质性和各向异性、测试设备、测试工艺、井壁污染、及测试方法局限性、测试人员素质等因素的影响，获得的试井储层参数只能代表周围煤储层平均值，不能完全客观地、准确地反映煤储层的实际情况。现有的试井数学解释模型与实际煤储层也存在差距，充分考虑我国煤储层特点，针对性开发煤层气试井资料解释模型及试井资料分析方法是未来研究重点。同时对现场实际而言，试井方法测试成本很高，通过室内相似模拟物理试验，可控制研究成本，减少外部干扰，验证试井解释模型的准确性，有利于试井方法的进一步研究。

(2)实验渗透率受到尺度效应、贾敏效应等的影响，导致原煤柱样、成型煤样比试井渗透率低得多。由于条件限制，无法做到对煤储层复杂赋存状态的精确模拟，另一方面，取样制样过程会在煤样内部产生扰动，改变煤样内部应力状态，导致裂隙变化，使室内实验样品很难具有代表性，尤其是构造煤不能够制定原煤样。此外，实验室煤样测试的最大尺寸为直径75 mm、高150 mm的圆柱型煤样，不可能包括原位煤储层中大的裂隙，这也导致目前实验室条件下无法真实模拟原位煤储层渗透率。因此，实验渗透率不能完全代表原位煤储层渗透率。但可大致反映煤储层渗透率的状况。然而现今实验渗透率测试行业标准不统一，建议制订统一方法、仪器、煤样尺寸、围压、储层压力、温度及同一流体介质条件下的渗透率测试国家标准。

(3)现阶段的渗透率模拟模型中，无论是实验研究还是数值模拟，均为基于某方面假定，得到某一条件下的渗透率，如假设基质体积收缩与等效吸附压力的降低成正比、假设基质体积收缩与解吸气体的体积成正比或假设裂隙压缩系数为常数等等。但是煤储层作为一种连续各向异性非均质介质，渗透率具有多因素性、随机性、模糊性的特点，上述的假设仅出于理想状态的考虑，能够做到对渗透率趋势变化的预测，但不能做到对渗透率的精确刻画。同时关于不同边界条件的模拟设定，现阶段仍没有足够证据证明哪个更适用于煤储层渗透率这个复杂非线性参数的模拟，其适用性有待进一步研究。

(4)煤储层渗透率研究涉及煤基质块、气及水(油)三相介质，宏观裂隙、微观裂隙及孔隙三元结构系统，吸附/解吸、扩散及渗流、紊流等多级流动。但由于压降和渗流速度在裂隙与煤基质内存在差异，就导致在煤体内部事实上存在2个非连续压力渗流场。目前多见单孔或双孔连续介质渗流模型，对三元结构系统模型鲜见报道。若将地质模型、数学模型、计算机模型等手段有机结合起来建立综合模型，其模拟、预测的渗透率将越来越接近煤岩体的真实渗透率。

(5)无论是通过建立煤储层渗透率与单一主控因素之间的定量关系进行预测，还是利用现代计算机技术通过神经网络及支持向量回归机等方法进行预测，其本质都是通过已经获取的煤储层相关参数来预测相似储层条件下的未知区域的渗透率。作为一个非线性参数，渗透率的影响因素非常复杂，受各种影响因子的耦合控制，这导致现有渗透率预测方法存在适用性问题，尽管可以通过灰色关联技术、多层次模糊综合评价等手段对不同影响因子进行优选或权重再分配，但仍会受到人为主观因素的干扰。