CT扫描的煤岩面裂隙椭球模型重构与张量表征及其应用

王守光，穆鹏宇，王嘉敏，李海涛，齐庆新,2

(1.煤炭科学研究总院有限公司 深部开采与冲击地压防治研究院，北京 100013;2.煤炭资源高效开采与洁净利用国家重点实验室，北京 100013)

煤的天然裂隙结构对于其变形破坏力学行为具有至关重要的影响，精确观测和表征煤岩内部的天然裂隙结构具有重要的科学意义和工程价值。以光学显微镜、扫描电子显微镜(SEM)、透射电子显微镜(TEM)等为代表的表面观测技术为煤岩表面微细观裂隙结构观测和研究提供了极大的方便，而后以计算机体层摄影(CT)扫描技术等为代表的内部观测设备实现了对煤岩内部裂隙结构的精确观测。第1台CT扫描机于1967年在英国研制用于医学临床诊断，而后发展出了工业CT和微米CT。我国许多科研单位根据不同使用需求购置和研制了工业CT系统，并取得了一系列重要的研究成果。近年来煤炭科学研究总院有限公司也购置了最新的CT扫描系统，可扫描样品的最大尺寸为500 mm×1 000 mm，居国内前列。CT扫描实验通过获取煤岩内部裂隙图像，利用计算机图形分析技术进行裂隙坐标计算和三维图像重构；例如文献[6-15]的工作。利用CT扫描图像进行裂隙结构三维重构技术目前已经日趋成熟，例如Thermo Scientific公司开发的AVIZO三维可视化软件可以方便地完成这一工作。CT裂隙图像重构方便了对煤岩孔裂隙结构演化的直观认识，但要进行深入定量化研究就必须从三维裂隙图像中提炼出有概括性的数字指标。

当前煤岩体裂隙结构的定量描述方法大致分为如下4种：① 形态学方法。采用裂隙形态学指标，如长度、面积、倾向、倾角等因素量化描述裂隙结构的三维特征，描述指标直观、通俗易懂，但这样描述的问题是每个指标过于具体，描述范围窄。② 统计学方法。统计学方法立足于随机数学、统计学理论或极射赤平投影等地质学技术，通过描述裂隙结构的整体分布特征，建立裂隙结构整体分布规律与岩体物理力学性能的关系。例如岩石力学中常用的Barton方程、Hock-Brown强度准则、节理玫瑰图，以及伍法权等的统计岩体力学理论等。③ 分形维数理论。分形维数也是目前煤炭行业最常用的裂隙描述指标，其将分形几何理论与裂隙几何学等结合，提炼出了更具概括性的数学指标，即标量分形维数值，描述了裂隙的不规则程度，例如谢和平和鞠杨等的工作。分形维数理论基础完备，但标量理论限制了描述的维度，未来扩展到张量分形维数理论或许是一个发展方向。④ 除了上述3类主要方法外，一类基于张量的描述方法也得到了一定程度的应用，如组构张量和渗透率张量等。由于人们认识到，岩体裂隙结构具有强各向异性，单一标量指标难以完整反映裂隙场的性质，并且出于在岩体本构模型中反映裂隙场的需要，ODA发展了裂隙组构张量理论，SNOW等提出了渗透率张量解决含水裂缝介质渗透各向异性问题。然而，现有的裂隙张量描述方法主要应用于固体(包括岩体)损伤力学理论分析，在岩石工程中的实用性不足，尚未被岩石工程界广泛接受。

裂隙张量理论起源于复合材料力学和细观固体力学。1980年，KACHANOV针对弹性体裂隙提出裂隙张量的概念。ODA证明了裂隙张量实际对应于裂隙方向性概率密度函数，称其为裂隙组构张量。KANATANI创造性提出了以组构张量描述方向分布函数，并极大地完善了组构张量代数理论。YANG等做了大量的后续研究，提出了标量型方向分布函数、矢量型方向分布函数和张量型方向分布函数的概念，分别给出其组构张量解析解。然而，上述裂隙组构张量针对的是理论上的假想裂隙场，如图1(a)所示(图中，为第个裂隙微平面)，而CT扫描获得的煤岩真实裂隙场如图1(b)所示，显然，现有的裂隙张量理论无法表征图1(b)所示的岩体真实裂隙结构。

图1 理论假想裂隙场与煤岩真实裂隙场对比Fig.1 Comparison of the theoretically hypothetical micro-plane fracture model and the real fracture structure obtained by CT scanning of coal

对此，笔者提出对煤岩CT扫描获得的真实复杂面裂隙场进行三角网格离散与椭球模型重构，然后基于椭球模型对裂隙结构进行张量表征的全新研究思路。首先介绍了空间CT扫描裂隙结构的三角网格离散技术，然后提出了对三角形裂隙的椭球模型重构算法，实现用一系列旋转扁椭球模拟面裂隙空间分布，建立了控制方程并给出了其求解策略；进一步结合椭球模型，建立了新的裂隙张量计算理论，包括裂隙方向张量与裂隙组构张量；最后对裂隙张量表征理论与椭球模型重构算法开展应用研究和验证分析。

1 煤岩裂隙结构的CT扫描试验

采用埋深700多米的赵固一矿煤样，制作成直径40 mm、高40 mm的圆柱形煤样4块，利用天津三英精密仪器公司生产的nanoVoxel-4000 CT扫描系统对煤样进行CT扫描，并进行数字图像处理，如图2所示。CT扫描的主要参数为：空间分辨率15.12 μm，扫描电压180 kV，电流350 μA，曝光时间0.68 s，放大倍数6.614，帧数3 240。采用阈值分割的方法处理CT扫描图像将裂缝和基质分开；其中，裂缝的颜色较暗，基质颜色较亮，且基质的密度越大颜色越亮(由于材料密度越大，X射线衰减越大，图像越白)。图像分割阈值在1～65 535(16位灰度)，且值越高图像颜色越亮，本实验所采用的分割阈值大致为23 513左右。

图2 煤岩内部裂隙结构的CT扫描与图像处理流程Fig.2 CT scanning and image processing of the internal fracture structure in coal

由上述方法获得的煤岩CT扫描裂隙二维切片图及三维结构图如图3所示，二维切片图右上角的数值表示切片的编号。由CT扫描实验知，该煤岩内部裂隙结构主要以面裂隙为主，仅有少量的孔隙；面裂隙的厚度为20 μm左右。

2 煤岩面裂隙的椭球模型重构算法

由于CT扫描获得的煤岩面裂隙结构有着非常复杂的几何形态与边界，造成它既难以被有效地描述，也很难从理论上研究它对煤岩力学特性的影响，因此对真实裂隙形态的合理简化十分必要。据此，笔者提出一种对煤岩CT扫描得到的真实裂隙场进行三角网格离散与椭球模型重构的简化方法。

2.1 煤岩面裂隙的三角网格离散技术

如图2所示，在Avizo软件中对煤岩CT扫描获得的裂隙结构进行数字图像处理，可以导出包含裂隙结构点、线、面信息的.obj文件，文件内容如图4所示，其自动将裂隙结构面离散化为多个三角形面，给出了各个三角形面的顶点编号和坐标值(Avizo软件中导出的.stl文件经Geromagic Wrap软件处理也可得到与此格式相同的.obj文件)。

图3 煤岩内部裂隙结构的CT扫描Fig.3 CT scanning diagram of coal fracture structures

图4 煤岩CT扫描裂隙的.obj文件格式Fig.4 Format of the .obj file of coal fractures

将.obj文件导入Geromagic Wrap软件中，利用软件的多边形或精确曲面功能，可进一步简化和修复三角形网格(图5)，简化前某空间裂隙由84 762个三角形面组成，简化后减少为42 000个三角形裂隙面。

图5 面裂隙三角形网格简化前后对比Fig.5 Comparison before and after simplification of triangular mesh of planar fractures

2.2 煤岩面裂隙的椭球模型重构算法

针对离散得到的三角形面裂隙，设计一种特殊的面椭球，即旋转扁椭球(使面椭球两长轴的长度相等)拟合每个三角形裂隙面，如图6所示，最终实现用一系列旋转扁椭球模拟空间面裂隙的分布。图6中，用，，表示椭球体的3个主轴，主轴长度等于面裂隙的厚度，每个旋转扁椭球的横截面均为圆形，半径等于和。

图6 煤岩面裂隙的椭球模型重构示意Fig.6 Reconstruction diagram of coal fractures by ellipsoids

面裂隙椭球重构算法的目标是寻求任意给定边界三角形裂隙面的椭球体拟合最优解。分别给出二维空间和三维空间中三角形面裂隙椭球重构的控制方程和求解策略如下：

2.2.1 二维空间中三角形面裂隙重构控制方程

如图7所示，对于由CT扫描得到的裂隙结构，每个三角形顶点坐标是已知的。在二维空间中，三角形面裂隙的椭球重构是一个双目标约束优化问题：目标是使拟合裂隙面的椭球片数量最小、同时拟合覆盖率最大。

记椭球片数量为，覆盖率定义为

(1)

式中，,,…,椭球圆截面(以下简称圆片)半径；为三角形面积，0<<1。

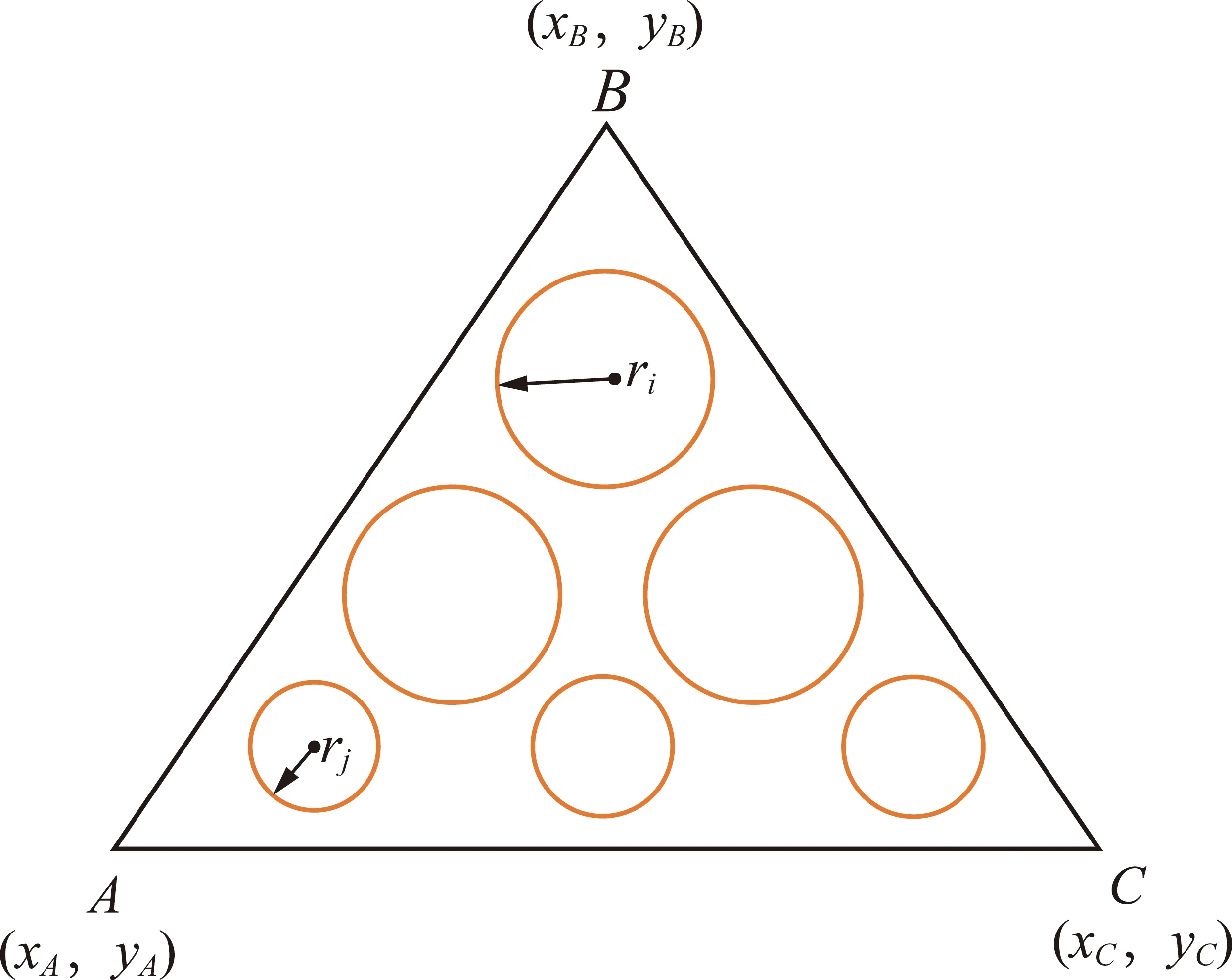
图7 二维空间三角形裂隙面椭球重构示意Fig.7 Schematic diagram of ellipsoid reconstruction of triangular fracture surface in two-dimensional space

目标条件的数学表达式为

min()=min{1-,}

(2)

其中，变量={,,…,,,,…,,,,…,,}。

约束条件是使所有椭球体位于三角形内部，且互相不覆盖。其约束方程为

(1)圆片之间不覆盖条件：

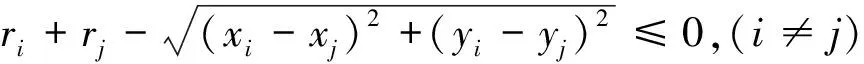
(3)

式中，(,)为第个圆片的圆心坐标；为第个圆片的圆心坐标。

(2)圆片与三角形边界不覆盖条件：

-≥,-≥,-≥

(4)

其中，，，为三角形的顶点，第个圆片圆心(,)到三角形边的距离-为

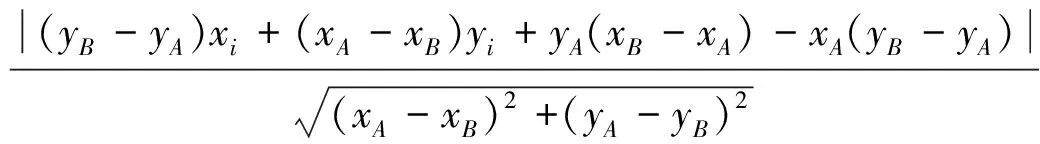
(5)

同理可写出-，-的表达式。

(3)约束圆片在三角形内部：

(，)(,)>0

(6)

(，)(,)>0

(7)

(，)(,)>0

(8)

其中，，和分别为直线、直线、直线C的方程，其表达式分别为

=(-)(-)-(-)(-)

(9)

=(-)(-)-(-)(-)

(10)

=(-)(-)-(-)(-)

(11)

2.2.2 三维空间中三角形面裂隙重构控制方程

三维空间中面裂隙椭球重构的目标函数形式与二维空间完全相同，区别在于变量的维度扩充：={，,…，，,…，，,…，，,…}。以二维空间中的约束条件为基础可以提出三维空间约束条件：

(1)圆片之间不覆盖条件

(12)

(2)圆片与三角形边界不覆盖条件

-≥,-≥,-≥

(13)

其中，第个圆片圆心(,,)到三角形边的距离-为

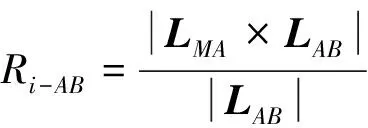
(14)

其中，=(-,-,-)，=(-,-,-)。同理可写出-,-的表达式。

(3)约束圆片在三角形内部

① 约束圆片圆心在平面内：

×·=0

(15)

② 约束圆片与平面重合：

·=0,·= 0,=min{1,2,3}

式中，为椭球圆截面法线方向向量；和分别为边和边的方向向量；1,2,3分别为椭球体3个主轴的焦半径。

③ 约束圆片圆心在三角形内部：

在三维空间中约束圆片圆心在三角形内部较为复杂，笔者提出一种简化约束方法，即将圆片圆心(设为点)与三角形投影至坐标平面内进行约束，如图8所示，当平面不垂直于面时投影至坐标面(当平面垂直于面，此时需往其他坐标面投影)，此时约束条件可写为

′′(′,′)′′(′,′)>0

(17)

′′(′,′)′′(′,′)>0

(18)

图8 圆片圆心与三角形向坐标平面投影Fig.8 Projection of circle center and triangle to coordinate plane

(19)

式中，′′，′′和′′分别为直线′′、直线′′、直线′′的方程，点′，′，′，′为点，，，的投影点。

2.2.3 控制方程的求解

以二维空间中面裂隙重构控制方程为例，讲解裂隙重构双目标约束优化问题的求解思路如下：

首先将双目标约束优化问题转化为单目标约束优化问题，即算法1：

算法1 双目标优化转化为单目标优化问题 n=1; nmax=20; while n≤nmax min(1-K) s.t.式(3)～(11) 判断是否接受此时的X:若接受,跳出while循环;若不接受,continue; n=n+1;end输出X

算法1的核心是单目标约束优化问题的求解。将该单目标约束优化问题整理如下：

目标条件：

(20)

约束条件：

(21)

式中，系数,,…，，,,…，为与三角形顶点坐标有关的常数，根据式(4)～(11)，其表达式不难列出。

显然该约束优化问题属于不等式约束优化问题，可采用KKT条件求解该问题。

(1)构造广义拉格朗日函数：

(22)

其中，为椭球体的数量；为待定系数。

(2)列出KKT条件：

(23)

根据式(1)～(23)在MATLAB软件中编写了计算程序，可自动列出KKT条件的定解非线性方程组。例如对任意空间三角形裂隙面，当只用1个旋转扁椭球拟合时，即=1(的选取与可接受的椭球覆盖率有关)，此时定解方程组为九维三次非线性方程组，如图9(a)所示，其中，和分别为旋转扁椭球圆截面的半径和圆心坐标(,)；～分别为～。

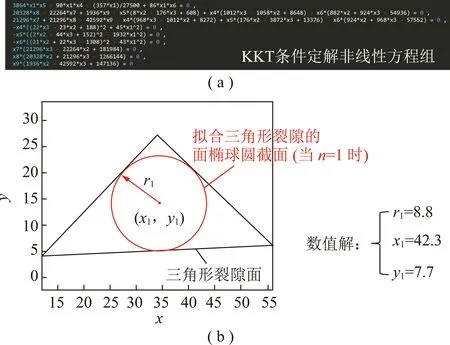
图9 控制方程求解算法的验证分析Fig.9 Verification analysis of the governing equations’solving strategy

最后，可采用Newton迭代法或修正的Newton迭代法求解定解非线性方程组，对于图9(a)所示的方程，用牛顿法求得其数值解如图9(b)所示，绘出三角形裂隙与旋转扁椭球圆截面的位置关系，发现数值解恰是三角形内切圆的圆心和半径值。由于内切圆是三角形中面积最大的区域，因此三角形裂隙面的最佳拟合为其内切圆符合常理，验证了上述求解策略的正确性。

2.2.4 特殊条件下的理论解

当拟合同一三角形的椭球片数量增加时，待解非线性方程数目将急剧增加，可能导致方程求解不收敛，为此需要寻找椭球模型重构的解析方法。若在网格处理时将图5中的三角形裂隙面均调整为正三角形，此时可使用解析方法。仍以二维空间求解为例(事实上很多三维空间中的拟合问题可通过坐标变换转变为二维空间中的拟合问题)，如图10所示，设任意正三角形的边长为，与水平线夹角为，其椭球体拟合的理论解求解步骤如下：

(1)寻找正三角形底点、确定三角形的底边。

底点是指3个顶点中纵坐标最小的点，记为(,)；底边上为底点和其他2个顶点中横坐标最大的点的连线，记底边另一顶点为(,)。

(2)计算三角形底边与水平线的夹角(0°≤<120°)。

当=，=90°。

(3)沿底点旋转三角形底边，使其水平放置。

底边绕底点(,)旋转得到新底边，新底边上另一顶点记为(′,′)，则

(24)

(4)计算旋转后正三角形的椭球体拟合，给出椭球圆截面的圆心和半径解析公式，见表1。

(25)

需要注意的是，当给出13个圆片拟合三角形时，如图11所示，已经可以取得较好的拟合精度，此时椭时覆盖率为87.3%。

(5)计算初始正三角形椭球体拟合的椭球圆截面圆心坐标。

再将新底边绕底点(,)反向旋转得到原有图形，进而得到原图形的圆片拟合圆心坐标值：

(26)

图10 正三角形裂隙面椭球体拟合过程示意Fig.10 Diagram of rotation of random regular triangle

表1 旋转后正三角形裂隙面椭球体拟合的椭球圆截面圆心和半径解析解Table 1 Analytical solutions of the circle center and radius of ellipsoids to reconstruct the rotated regular triangles

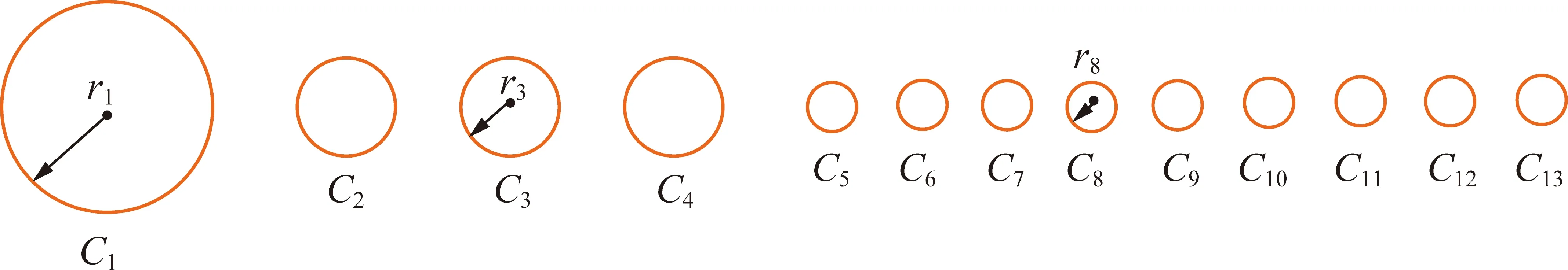
图11 正三角形裂隙面三级拟合的椭球圆截面示意Fig.11 Circular sections fitted by an equilateral triangle ellipsoid

3 煤岩面裂隙的张量表征

3.1 裂隙张量的构造

有了椭球模型拟合裂隙结构，即可基于椭球体计算裂隙张量，进而表征整个裂隙结构的性质。1980年，KACHANOV提出形如式(27)的裂隙张量表征细观裂隙：

(27)

式中，为裂隙张量；为裂隙体积；为裂隙圆盘半径；为裂隙法线方向向量。

笔者结合煤岩CT扫描面裂隙的性质，提出两类新的裂隙张量，即裂隙方向张量和裂隙组构张量如下：

面裂隙方向张量：

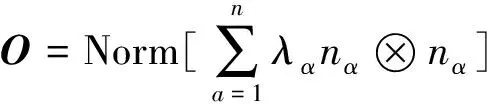
(28)

式中，=min{1,2,3}为椭球体圆截面法线单位向量；Norm表示矩阵归一化；为与裂隙面积相关的权重系数，=1,2,…,。

面裂隙组构张量：

(29)

其中，,为第个椭球的第个主轴，=1,2,…,，=1,2,3；,为椭球体3个主轴的主轴长度；,为椭球体3个主轴的方向向量。但由于面椭球具有：1=2≫3的特点，因此，面裂隙组构张量可进一步简化如下：

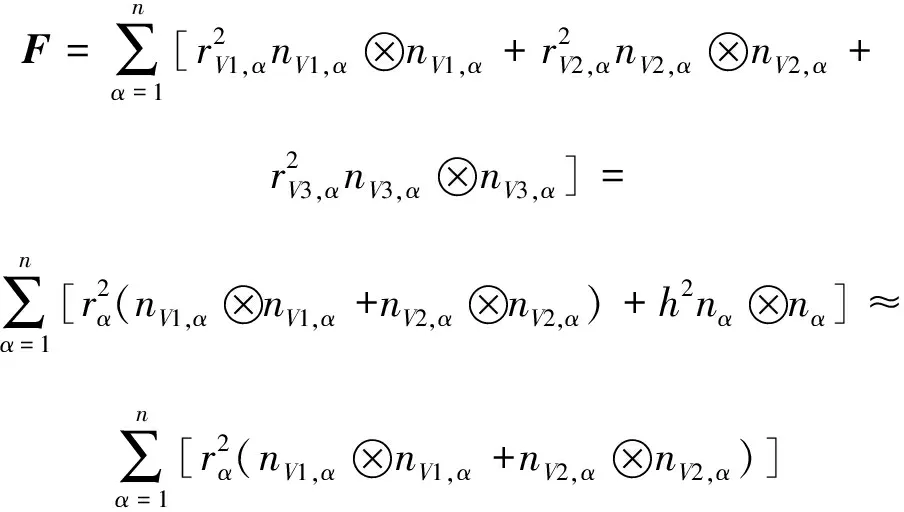
(30)

式中，为第个椭球的圆面半径；为裂隙厚度。式(30)的推导过程利用了≪的事实。

3.2 两类裂隙张量的性质

面裂隙方向张量显然只与面法线方向有关，与面尺寸无关。因而计算面裂隙方向张量可直接依据面裂隙三角形顶点坐标，避开了椭球体拟合。

对于面裂隙组构张量，先证明这一结论：空间圆片任意2条相互垂直的半径向量，其张量积之和为定值。如图12(a)所示为整体坐标系下的空间圆片，图12(b)为其对应的局部坐标系下描述。由图12(b)知，局部坐标系下任意2条相互垂直的半径向量分别为

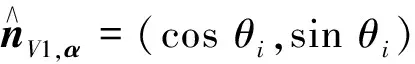
(31)

(32)

式中，为一任意半径与轴正方向的夹角；上角标∧表示在局部坐标系下描述。

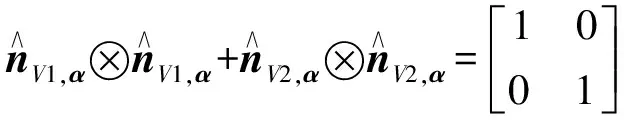
(33)

设为局部坐标系到整体坐标系的坐标变换矩阵，则式(30)中的张量积可化为

(34)

由于坐标变换矩阵只与裂隙面走向及倾角有关，对于确定的圆面(确定了坐标变换矩阵)，上式应为一固定值。这说明了面椭球圆片内主轴方向的选取对组构张量计算没有影响。

(35)

式中，，分别为三角形和其内切圆的组构张量；为比例系数；，分别为三角形和其内切圆的面积。

3.3 面裂隙张量的简便算法

式(35)的核心是求解任意空间三角形内切圆的组构张量，使用图9的方法可以计算出三角形内切圆圆心、半径等参数，但计算较为繁琐。下面结合图13给出更简单的计算方法。

(1) 计算三角形内切圆半径：

(36)

式中，,,为三角形3条边长。

(2)计算角平分线方向向量′：

(37)

(3)根据′计算角平分线上一点′坐标。

(4)计算′到直线距离：

(38)

(5)计算：

(39)

(6)根据计算内切圆圆心坐标。

(7)联合式(28)计算内切圆方向张量，其中：

=×

(40)

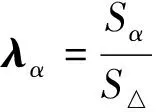
(41)

(8)联合式(30)计算内切圆组构张量，其中

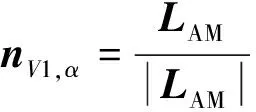
(42)

2,=1,×

(43)

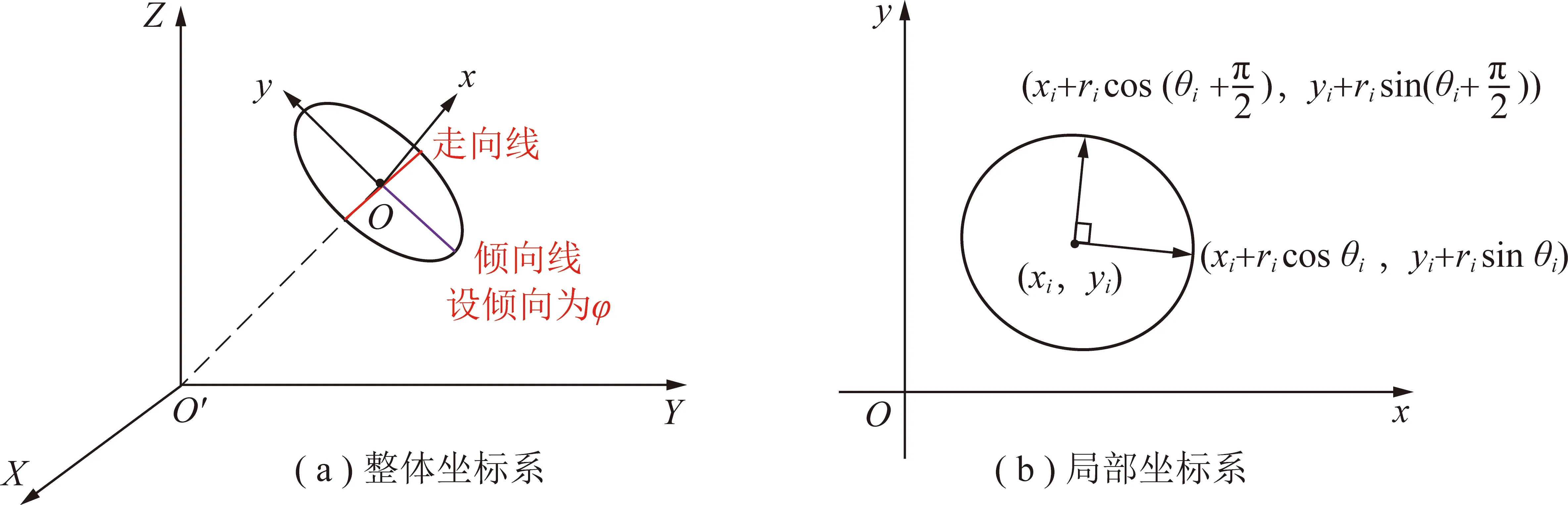
图12 空间圆片在两种坐标系下的描述Fig.12 Description of space wafer in two coordinate systems

图13 空间三角形及其内切圆计算示意Fig.13 Calculation diagram of spatial triangle and its inscribed circle

4 裂隙张量表征理论的应用

4.1 简单裂隙的张量表征

如图14所示，对于一圆柱形试样，内含一个45°的币状裂隙面，该裂隙厚度为0.1 mm，直径为10 mm。利用式(28)～(30)和(35)～(43)可以计算裂隙方向张量和裂隙组构张量(单位：mm)如下：

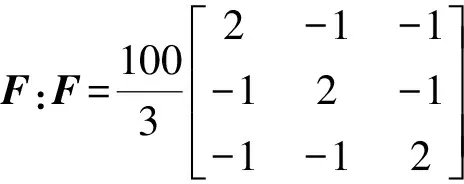
图14 空间圆柱体含45°币状裂隙面Fig.14 Space cylinder with coin shaped fracture surface of 45 degrees angle

4.2 CT扫描裂隙的张量表征

下面选取图3(b)中煤样的CT扫描裂隙结构，对其进行张量表征。该煤样尺寸为40 mm×40 mm，从图15中可以将其裂缝结构划分为3个优势裂缝组：优势裂隙组①的倾角为0°，面积约209.4 mm；优势裂隙组②的倾角为75°，面积约190 mm；优势裂隙组③的倾角为90°，面积约424.2 mm。利用这些数据，结合式(28)～(30)和(35)～(43)，可以给出这3个优势裂隙组的方向张量和组构张量，并根据面积加权平均得到整体裂隙结构的张量表征。

笔者已利用式(1)～(43)自主开发了一套煤岩面裂隙方向张量与组构张量计算软件FTCS(软著登记号：2021SR0342359)，该软件可直接读取Geomagic软件导出的裂隙三角网格数据.obj文件，生成煤岩结构面的方向张量与组构张量。计算结果如下，其中裂隙组构张量的单位均为mm。

图15 煤岩CT扫描裂隙结构优势裂隙组划分Fig.15 Diagrams of coal sample and its CT scanning fracture structure

(1)优势裂隙组①(0°倾角)。

(2) 优势裂隙组②(75°倾角)。

(3) 优势裂隙组③(90°倾角)。

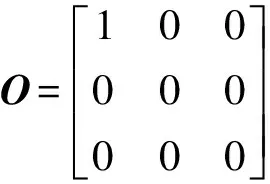
(4) 整体裂隙结构。

4.3 裂隙场演化过程的张量表征

再将埋深700多米的赵固一矿煤样，制作成直径50 mm、高100 mm的圆柱形煤岩标样，在TAW-2000岩土力学试验机上开展单轴压缩试验，分别把不同加载阶段的煤岩进行CT扫描，分析其裂隙结构的演化过程。试验采用力控制，加载速率均为0.05 kN/s。对其破坏过程进行分析，采用方向张量、方向张量增量、组构张量、组构张量增量及各张量的迹(即张量对角线分量之和)描述裂隙演化，并与裂隙的面积、孔隙率和分形维数等描述方法对比分析。其中，孔隙率为裂隙体积除以煤岩总体积，分形维数采用Hausdroff容量维数计算。裂隙张量的计算结果如图16所示，张量正下方红色括号内的红色数字表示张量的迹，所有组构张量的单位均为mm。

由图16可知，在加载过程中，裂隙面积和体积增大，孔隙率增多；分形维数也在增加，表示裂隙的不规则程度(或粗糙度)增强。裂隙扩展过程中，方向张量增量的迹变化量分别为-0.001 51，0.004 3，均远小于方向张量的迹(2.98)，可以认为裂隙平均方向改变很小，而从CT扫描图中也能看出新增裂隙面主要沿原有裂隙面方向扩展，裂隙平均方向改变不大，两者在定性上是吻合的。而裂隙组构张量的迹变化量分别为621，2 649，此时裂隙面积的实际变化量分别为5 925，20 183，两者是同步增大的关系，通过裂隙组构张量的迹变化量能够大致了解裂隙面积的实际变化幅度。由此可见，裂隙方向张量增量的迹与裂隙平均方向改变量、裂隙组构张量的迹与裂隙面面积变化量存在正相关关系，但深入的定量关系仍需要进一步探究。

5 裂隙椭球模型重构方法的应用

5.1 CT扫描裂隙结构椭球模型重构的精度分析

针对图16所示的10号煤样初始裂隙，在Geomagic Wrap软件中简化后得到的三角形面片约11万片，经椭球模型重构得到的裂隙椭球片近30万片。但目前对于如此数量众多的椭球体片可视化仍存在较大困难，因此对近30万片椭球体进行了检索和挑选，并合并一些方向相同但尺寸较小的椭球体片，自主开发python程序，实现了对椭球模型重构结果的可视化。如图17所示，简化后的椭球体片约1万片左右。经过与CT扫描裂隙的对比发现，利用本文椭球重构方法得到的裂隙结构模型能够较好地表征由CT扫描得到的真实裂隙结构；并且，通过控制和修正部分椭球片的尺寸，本文的椭球体裂隙模型可以100%拟合真实裂隙结构(指在面积和体积上相同)，以图17为例，这两个裂隙结构的裂隙总面积均为3 279.1 mm，裂隙总体积均为162.9 mm。

5.2 基于椭球模型重构的裂隙煤岩等效弹模预测

在研究裂隙结构对固体(或岩体)变形性质的影响时，固体力学界给出了许多十分重要的理论方法，如Eshelby椭球夹杂理论、Mori-Tanaka方法、Gurson模型以及能量方法等，而上述理论都对天然裂隙或孔隙进行了简化，假设为椭球体或球体，但真实的裂隙结构并非椭球形，导致理论和实际难以联系。笔者提出的椭球模型重构方法或许能够搭建起以上固体力学理论与岩体真实裂隙结构之间沟通的桥梁。

图16 裂隙场演化的张量描述与孔隙率、分形维数的对比Fig.16 Comparison of tensor description of fracture field evolution compared with porosity and fractal dimension descriptions

结合图17，对由CT扫描获得的煤岩真实裂隙场进行椭球模型重构，将得到一系列椭球体模型拟合真实裂隙结构，再利用Eshelby椭球夹杂理论等细观固体力学方法，就可以建立裂隙煤岩等效弹性模量预测的理论模型。本节以椭球模型重构方法与Mori-Tanaka模型的结合为例，推导裂隙煤岩等效弹模预测的理论公式，公式推导过程中，综合参考了文献[34-35]中的求解思路。

图17 椭球模型重构算法的精度分析Fig.17 Precision analysis of the ellipsoidal reconstruction algorithm

如图18所示，Mori-Tanaka模型的基本思想是逐一将单个裂隙置于“无损基体”中，承受有效的应力应变场，而这种有效场与外加的远场不需要一致。因此，它本质是一种简化的有效场法。其基本假设为：① 应力场与应变场均匀；② 相变过程中，整体宏观应力水平保持不变。

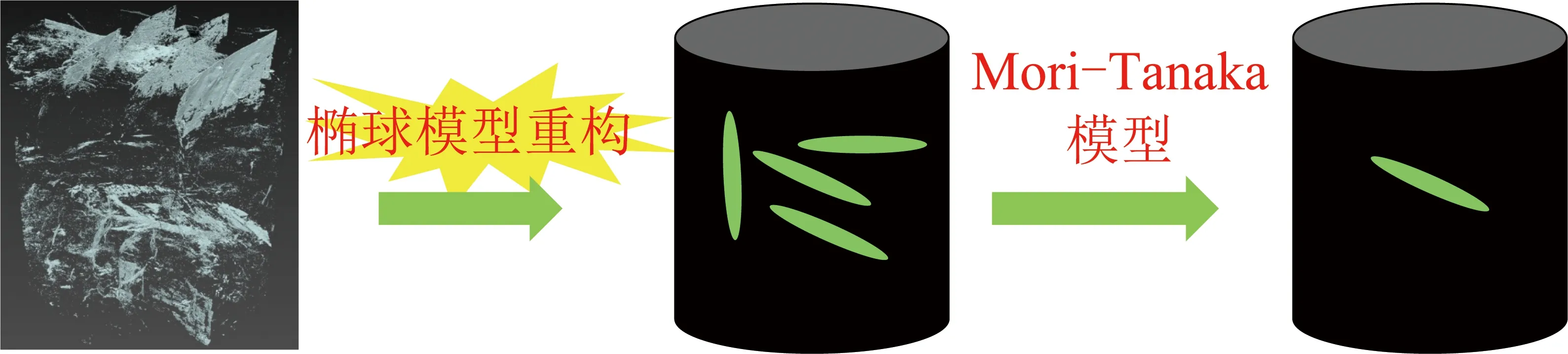
图18 含复杂裂隙煤岩等效弹性模量计算思路Fig.18 Calculation procedure of equivalent elasticity modulus of complex fractured coal

5.2.1 岩石基质的初始均匀化

如图19左侧所示，假设在没有裂隙存在时，岩石基质足够大，且均匀，其弹性模量张量为，其边界为Ω，体积为。此时在岩石基质边界上施加均匀外力场，产生均匀应变场。

图19 岩石基质代表性单元及相变示意Fig.19 Schematic diagram of representative unit volume and phase transformation of rock matrix

5.2.2 椭球体裂隙的引入

假设在均匀岩石基质的基础上发生局部相变，如图19右侧所示，产生体积为，边界为Ω的椭球形裂隙，裂隙弹性模量张量记为，应该有=0。设岩石基质相变时，裂隙对基体产生的平均扰动应力张量，裂隙内平均应力与基体平均应力差为，此时岩石基质平均应力张量为：+，裂隙平均应力张量为：++。

根据Eshelby等效变换理论，裂隙内平均应力可写为

++=∶(++)=∶(++-)

(44)

式中，为相变产生的扰动应变张量；为两相应变差值；为本征应变张量，且有

=∶

(45)

式中，为四阶Eshelby张量。

由式(44)和(45)得

++=∶+∶+∶∶-∶=++∶∶-∶

(46)

进一步得

=∶∶-∶

(47)

5.2.3 基于Mori-Tanaka模型的等效方法

由Mori-Tanaka等效应力法，相变前后岩石基质的平均应力保持不变。设=表示裂隙的体积分数，则

=(++)+(1-)(+)

(48)

式中，为裂隙的体积分数；为裂隙体积。

进一步得

=-

(49)

由式(47)和(49)得

=-=-∶(-)∶

(50)

进一步得

=-(-)∶

(51)

式中，为四阶单位张量。

将式(45)和(51)以及=0，代入式(44)，得

(-)∶(1-)=

(52)

其中，对于面椭球，四阶Eshelby张量为

(53)

其余元素为0。为四阶张量的一个分量；为泊松比。对于其他类型椭球体的四阶Eshelby张量计算公式请参考有关专著。

由于和均为已知值，由式(52)得本征应变张量：

(54)

设裂隙岩体等效应力应变关系式为

(55)

其中，

(56)

(57)

进一步得

(58)

简化得

(59)

则有

(60)

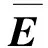
5.2.4 裂隙煤岩等效弹性模量的迭代求解

式(60)为单个裂隙影响下岩石等效弹性模量的计算公式。假设煤岩CT扫描裂隙被个椭球形裂隙拟合(例如图17中的30万个椭球片)，则计算它们整体对煤岩弹性模量的影响需要迭代法，即每次将上次含-1个裂隙的岩石当做“无损的”等效弹性介质，计算第个椭球形裂隙对裂隙煤岩的影响。由此可得所有个裂隙影响下岩石等效弹性模量的理论预测值。

5.2.5 等效弹性模量预测理论公式的初步验证

对等效弹性模量理论公式的实验验证目前较为困难，原因在于试验结果的离散性较大，尚需做大量实验得出统计规律才能有说服力。然而，通过数值模拟进行初步验证是可行的。笔者在拥有自主知识产权的非线性有限元程序TFINE中开展数值模拟验证研究，如图20所示，煤样的尺寸为50 mm×100 mm，弹性模量为20 GPa，泊松比为0.3。预置椭球形裂隙的尺寸为(20×20×10)mm，并通过增加椭球形裂隙的个数模拟裂隙体积分数的增加，将数值模拟得到的等效弹性模量计算值与理论计算结果对比，如图21所示。由图21知，当含有一个椭球形裂隙，此时裂隙的体积分数为1.06%，煤岩等效弹性模量的理论计算值与数值模拟结果仅相差1.37%；当含有2个椭球形裂隙，裂隙体积分数增加至2.13%，等效弹性模量的理论计算值与数值模拟结果相差4.8%；总体来说，当裂隙体积分数较小时，等效弹性模量理论预测误差可以接受。但进一步增大裂隙体积分数，理论计算得到的等效弹性模量与数值模拟相差越来越大，误差从7%增大到37%。因此，本文的理论公式对于裂隙体积分数较小时更为有效。

图20 含椭球形裂隙煤岩的单轴压缩模拟示意Fig.20 Diagram of uniaxial compression simulation of coal with ellipsoidal fractures

需要说明的是，Eshelby椭球夹杂理论和Mori-Tanaka模型均有适用范围，其主要针对细观力学，原因是它们都采用了应力应变均匀假设和裂隙满足叠加原理等。因此，上述理论公式仅对裂隙体积分数较小时适用是符合预期的。由图16知，天然裂隙煤岩的裂隙体积分数一般不超过2%，所以本文等效弹性模量理论公式应适用于分析煤岩受天然裂隙影响下的等效弹性模量预测。

图21 含椭球形裂隙煤岩等效弹性模量的数值模拟结果与理论计算值对比Fig.21 Comparison of equivalent elastic modulus of coal with ellipsoid fracture between numerical simulation and theoretical calculation

6 结 论

(1)针对由CT扫描试验获得的煤岩真实裂隙结构，本文提出了一套椭球模型重构算法，简化了真实裂隙场的复杂裂隙形态，实现了将难以被量化或理论研究的真实裂隙场转变成容易被量化或理论研究的椭球形裂隙场。算例验证表明，椭球模型重构算法的求解精度和拟合效果较好。

(2)在已有裂隙张量理论的基础上，提出了2类新的裂隙张量，即面裂隙方向张量与面裂隙组构张量，实现了对煤岩CT扫描裂隙场的张量表征。通过煤岩简单裂隙场、CT扫描得到的复杂裂隙场和煤岩破坏裂隙演化过程等3个具体案例，验证了裂隙张量理论对煤岩复杂裂隙结构及裂隙演化的描述能力，初步说明了裂隙方向张量与裂隙的平均方向性质、裂隙组构张量与裂隙面面积变化等存在定性的相关关系。

(3)介绍了椭球模型重构方法在裂隙煤岩等效弹性模量预测方面的应用，初步说明了椭球模型重构方法有助于建立煤岩CT扫描试验技术与细观固体力学理论之间沟通的桥梁，并利用数值模拟初步验证了弹性模量预测理论公式的可靠性。