考虑垂度影响的拉索-双粘滞阻尼器系统振动分析

孙利民，狄方殿，陈 林，邹易清

(1. 同济大学土木工程学院 桥梁工程系，上海 200092；2. 同济大学土木工程防灾国家重点实验室，上海 200092；3. 上海期智研究院，上海 200092；4. 柳州欧维姆机械股份有限公司，广西，柳州 545006)

自20 世纪80 年代以来，斜拉桥的跨径不断刷新记录，斜拉索的长度也随之增加。斜拉索的振动是此类桥极为棘手的问题，随着拉索长度的增加，该问题在设计和运营中变的更为突出。对于拉索不同类型的振动，目前工程中采用了多种控制措施，包括空气动力措施、阻尼器及辅助索等方法[1-5]。相比于其他措施，拉索上安装阻尼器仍然是目前最常用的方法。

对于拉索阻尼器减振系统的研究，最早可以追溯至Carne[6]和Kovacs[7]，他们的研究都是基于张紧弦理论，关注拉索在近锚端安装阻尼器时系统的一阶模态阻尼比。Carne 发展了一种近似的分析方法，并得到了与阻尼器阻尼系数和安装位置相关的拉索一阶模态阻尼比计算公式；Kovacs 则根据工程经验首次提出粘滞阻尼器阻尼系数优化问题，给出了一阶最优阻尼系数。Yoneda 和Maeda[8]结合工程经验，近似得到了阻尼器安装在近锚点时的拉索一阶模态阻尼比。Uno 等[9]引入无量纲化分析方法，方便了阻尼器的设计计算。Pacheco 等[10]采用Galerkin 方法计算得到了线性粘滞阻尼器的设计通用曲线，并简单分析了垂度的影响。Mehrabi 和Tabatabai[11-12]提出有限差分法，推导出了考虑拉索垂度和抗弯刚度后拉索振动的无量纲微分方程，研究结果表明拉索的垂度主要对拉索一阶模态阻尼比有明显影响，抗弯刚度对索获得的模态阻尼比有较大影响。Xu 等[13-16]提出一种混合方法，考虑拉索的平面内、外振动，研究了拉索的垂度、倾角、阻尼器刚度和安装位置对各阶模态阻尼比的影响。Krenk[17-18]给出拉索粘滞阻尼器的完整复模态分析方法。推导出阻尼器近锚固端安装条件下模态阻尼比的近似解析表达式。同时，Krenk 和Nielsen[19]也推导出有垂度拉索近端安装阻尼器阻尼比的近似解析表达式。Main 和Jones[20-22]重点针对拉索安装阻尼器后频率的变化进行了分析。在阻尼器安装在靠近拉索锚固点时，得到了与Krenk 一样的模态阻尼比近似解析式，并讨论了当阻尼器安装在拉索任一位置时超越方程的复特征值解的特点。

经过30 多年的发展，国内外学者对于拉索-阻尼器系统的研究不断深入，在分析模型的精细化[23]和系统频率、阻尼及响应计算方法方面均有重要改进。然而拉索阻尼器减振依然面临两个问题：① 位置限制，即阻尼器只能安装在拉索锚固端附近，而实际拉索所获得的最大阻尼比与安装距离成正比，因此，对于超长拉索来说，阻尼器安装位置的限制也势必造成拉索获得的阻尼不足；② 频率敏感性，虽然说阻尼器是一种广谱性的减振装置，但是使拉索某一阶振动获得最优模态阻尼的阻尼器阻尼系数，对于其他模态却不能达到最优。实际工程中通常是针对拉索的前几阶振动设计阻尼器参数，因此，对于拉索的高阶振动难以控制。随着拉索的增长，上述问题更为突出。因此，近年来学者更加关注负刚度阻尼器、拉索附加转动阻尼器、拉索安装双阻尼器等，以求提高阻尼器的减振效果。Krenk 和Hogsberg 等[17]发现当相应的阻尼器参数使其产生相位超前的控制力时，也即在阻尼器位置引入了负刚度，阻尼器的效果显著增大；此外，考虑阻尼器位置的附加质量时，阻尼器的效果同样增大，类似的是因为附加的集中质量相当于减小了拉索在此位置的刚度。传统振动控制中，负刚度效果需要通过主动或者半主动控制实现。近年来，一些被动负刚度、惯质装置陆续出现，在土木工程领域首先应用于建筑物的减隔震中[24]。Chen 等[25]以及Zhou等[26]建立了拉索附加负刚度阻尼器模型，并进行了理论分析。Chen 等[27]考虑拉索抗弯刚度研究了在索上单点同时安装横向和抗转动阻尼器以提升阻尼效果。

阻尼器由于安装高度的限制，随着拉索长度的增加，单点安装阻尼器抑制拉索振动越来越显不足。拉索上两处安装阻尼器(拉索-双阻尼器系统)有望弥补上述不足，且拉索同时安装外置阻尼器和内置阻尼器在工程中已有应用。Caracoglia 等[28]及Hoang 等[29]对拉索安装双阻尼器系统进行了研究，研究结果表明拉索安装双阻尼器后模态阻尼比是单阻尼器的两倍。国内外不少学者也对拉索安装不同类型的双阻尼器系统进行了研究[30]。上述研究的拉索模型均是基于张紧弦理论，对于超长拉索垂度影响是不容忽略的，为此，本文建立了有垂度拉索-双粘滞阻尼器系统模型，并推导出端部安装双阻尼器的拉索模态阻尼比近似解析式(双阻尼器安装在拉索两端、双阻尼器安装在拉索同一端)。分别分析了两端安装和一端安装双阻尼器后拉索的振动特性，研究双阻尼器参数关系对拉索模态阻尼的影响，对阻尼器参数进行了优化设计。研究成果可以为超长拉索双阻尼器设计提供计算方法及阻尼器参数设置依据。

1 拉索-双粘滞阻尼器系统的复特征频率方程

有垂度拉索-双阻尼器系统如图1 所示。考虑一水平放置的拉索，其弦长为L，水平张力为H，单位长度质量为m，轴向刚度为EA。拉索的抗弯刚度忽略不计。为了方便描述拉索的静位移和动位移，建立了如图1 所示的坐标系。拉索两锚固点连接方向假设为x轴 ，y(x)和v(x,t)分别表示拉索的静位移和相对静位移的动位移。

图1 有垂度拉索-双粘滞阻尼器系统Fig. 1 A shallow cable with two viscous dampers

对于土木工程领域常用的中小垂度拉索，其静止状态形状可以假定为抛物线函数[32]：

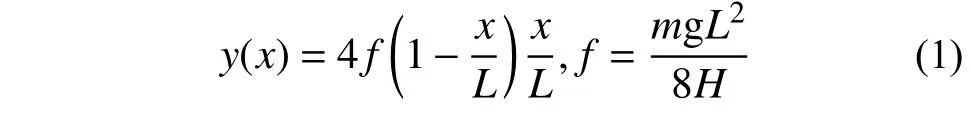
式中：f为拉索跨中垂度； g为重力加速度。

拉索被阻尼器分为3 个索段单元。为表示的方便，连接点用Pp编号，P0和P3分别表示拉索的左、右锚固点，两个粘滞阻尼器分别安装在P1和P2两点。lp为第p个拉索单元的长度(Pp-1和Pp点间距离)。定义各单元的局部坐标系，vp(xp,t)为第p个拉索单元在t时刻的竖向动位移，水平xp轴由Pp-1沿着索弦线指向Pp点。拉索振动产生一个随时间变化的附加水平张力h(t)，忽略拉索自身阻尼。各拉索单元的振动方程可以写成如下的形式：

拉索振动中其在附加水平张力h作用下发生弹性变形。假定索伸长后，拉索微元由初始长度ds变 为 ds′，沿索弦线的张力增量为h(ds/dx)。根据索的弹性关系可以得到下式：

其中，最后一项表示拉索上某点从初始位置(x,y) 变化为 (x+u,y+v)。

考虑拉索在锚固点的边界条件，式(3)乘(ds/dx)2并在索跨长内积分可以得到：

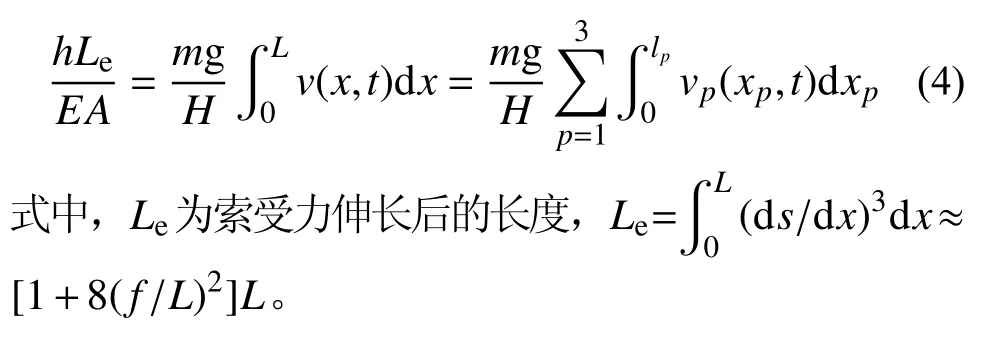
仅考虑索平面内的自由振动时，式(2)的解通常具有以下形式：

式中：ω为复频率；；为振型函数；为拉索附加水平张力幅值。将式(5)代入式(2)，可以得到：

化简式(4)得到：

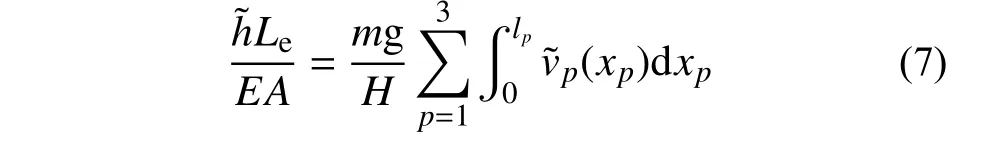
各拉索单元左、右端的竖向振动分别用νp-1(t)和νp(t) 表 示，对于自由振动有νp-1(t)=exp(iωt)和νp(t)=exp(iωt) 。因此，可以由下式得出：

注意到：

其中 θ为拉索倾斜角度。

式(10)乘以 ( βL)3可以得到：

根据拉索附加阻尼器位置内力平衡条件，进一步可得：

式中，cp为第p个阻尼器的阻尼系数。

最后，由式(11)和式(13)可得如下3 个方程：

将式(14)写成矩阵的形式，得到：

式中：

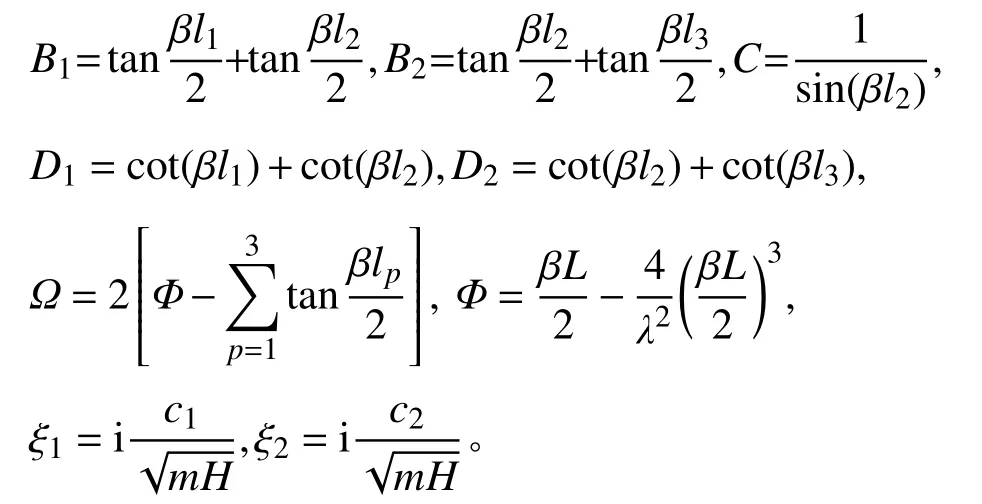
拉索-双粘滞阻尼器系统的复频率特征方程由式(15)系数矩阵的行列式等于0，得到：

式中：

2 拉索-双粘滞阻尼器系统方程求解

考虑阻尼器安装于索近锚固端，可以求解索附加模态阻尼比的近似解析解。本节考虑双阻尼器分别安装在拉索的两端和安装在同一端两种情况。

2.1 近似对称振型

2.1.1 阻尼器两端布置

式(16)可以写成如下的形式[32-33]：

利用三角函数变化，并考虑l1和l3远小于L，式(17)可以简化为：

式(18)等号左边可写成如下形式：

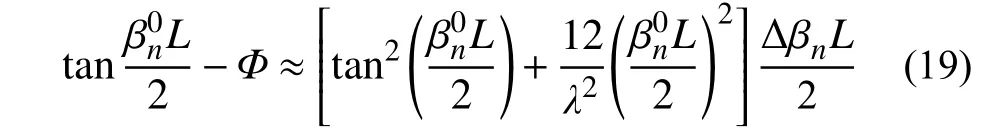
将式(19)代入式(18)，并对式(18)中三角函数级数展开取一阶小量，式(18)可以写成如下形式：

式(22)为近似对称振型下拉索在两端安装粘滞阻尼器时系统模态阻尼比的近似解析式。该公式 包 含κ、ρ、ε 及 垂 度 相 关 参 数λ2。当 ε=0 时，式(22)变为有垂度拉索安装单个阻尼器时的模态阻尼比计算公式[19]。

2.1.2 阻尼器同端布置

两个阻尼器相邻安装，即l1和l2远小于L。以阻尼器1 为参照，令 ρ=l2/l1。可以得到：

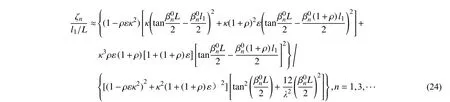
式(24)为近似对称振型下拉索在一端安装粘滞阻尼器时，系统模态阻尼比的近似解析式。该公 式 包 含κ、ρ、ε及λ2。当 ε=0 时，式(24)变 为有垂度拉索安装单个阻尼器时的模态阻尼比计算公式。

2.1.3 最优附加模态阻尼比

1)两端安装阻尼器

式(22)对κ求导，令 d(ζn(l1/L)-1)/dκ=0，可得到最优值。

① 当 ε=0时，表示拉索安装单个阻尼器。此时最优阻尼器参数κopt=1，对应最优阻尼为：

2)同端安装阻尼器

式(24)对κ求导，令 d(ζn(l1/L)-1)/dκ=0。

2.2 近似反对称振型

2.2.1 阻尼器两端布置

为了便于推导，将式(16)写成如下的形式：

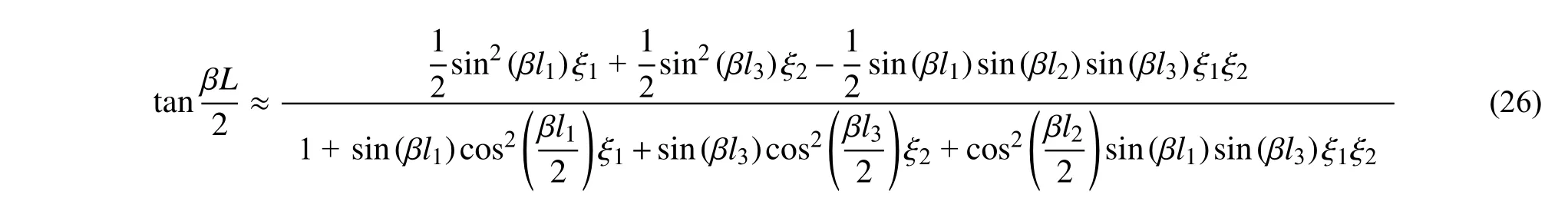
式(26)等号左边可以近似为 ΔβnL/2。考虑到l1和l3远小于L，对三角函数级数展开并取一阶小量，式(26)可以写成如下形式：

为了分析方便，以阻尼器1(l1≠0、ξ1≠0)为参照，令 ρ=l3/l1。则式(27)可以写成如下形式：

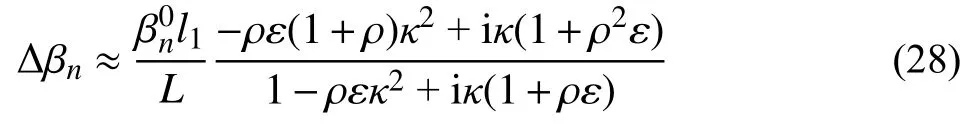
对应拉索模态阻尼比为：

式(29)为近似反对称振型下拉索在两端布置粘滞阻尼器时系统模态阻尼比的近似解析式，该公 式 仅 包 含3 个 参 数，即κ、ρ、ε 。 当 ε=0 时，式(29)即为拉索安装单个粘滞阻尼器时的模态阻尼比计算公式[10]；对于无垂度拉索，式(29)则为任意振型下拉索安装双阻尼器后模态阻尼比的计算公式[28-29]。

2.2.2 阻尼器同端布置

两个阻尼器相邻安装，即l1和l2远小于L。阻尼器1 为参照，令 ρ =l2/l1。可以得到：

式(30)为近似反对称振型下拉索在一端安装双粘滞阻尼器时，系统模态阻尼比的近似解析式，该公式也只包含κ、ρ、ε 三 个参数。当 ε=0时，式(30)退变为拉索安装单个粘滞阻尼器时的模态阻尼比计算公式；对于无垂度拉索，式(30)则为任意振型下拉索一端安装双阻尼器时模态阻尼比的解析表达式[29]。

2.2.3 最优附加模态阻尼比

1) 两端安装阻尼器

式(29)对κ求导，令 d(ζn(l1/L)-1)/dκ=0，则可得到最优阻尼器参数及对应的附加阻尼比。

① 当 ε=0时，表示拉索安装单个阻尼器。此时κopt=1 ， ζn,opt(l1/L)-1=0.5，与文献[5]结果相吻合。

② 当 ρ=1、ε=1时，表示2 个参数相同的阻尼器在拉索两端对称安装。此时，κopt=1，ζn,opt(l1/L)-1=1。这种情况下，拉索所获得的最大模态阻尼比是对应安装单个阻尼器的2 倍。

③ 当 ρε=1,κopt=1 ， ζn,opt(l1/L)-1=(1+ρ)/2。由于 0≤ρ≤1 ，所以该情况下 ζn,opt(l1/L)-1最大值为1，即为②中所述的情况。当 ρ不断减小时，即阻尼器2 的安装距离不断减小， ζn,opt(l1/L)-1值也不断减小，当 ρ减小到0 时，即为①中所述情况。

2) 同端安装阻尼器

式(30)对κ求 导，令 d(ζn(l1/L)-1)/dκ=0。

① 当 ε=0时，表示拉索安装单个阻尼器。此时κopt=1 ， ζn,opt(l1/L)-1=0.5。

② 当 ρ=0、ε=1时，表示2 个相同参数的阻尼器安装在近索端同一位置，此时κopt=0.5，ζn,opt(l1/L)-1=0.5。这时拉索所获得的最大模态阻尼比与同位置处安装一个对应参数的阻尼器相同。可见，在拉索端部同一位置安装双阻尼器并不能提高拉索的模态阻尼比，只是减少了阻尼器的尺寸。

3 拉索-双粘滞阻尼器系统参数分析

3.1 近似反对称振型

为了验证近似解的正确性，选取典型工况与数值解进行对比，数值解采用幅角原理(APM)方法[27]求得。后续近似解也进行对比验证，不再特别说明。

由式(22)可知，对于拉索近似对称振型的振动，垂度为一个影响因素。分析垂度的影响，计算得到图2。

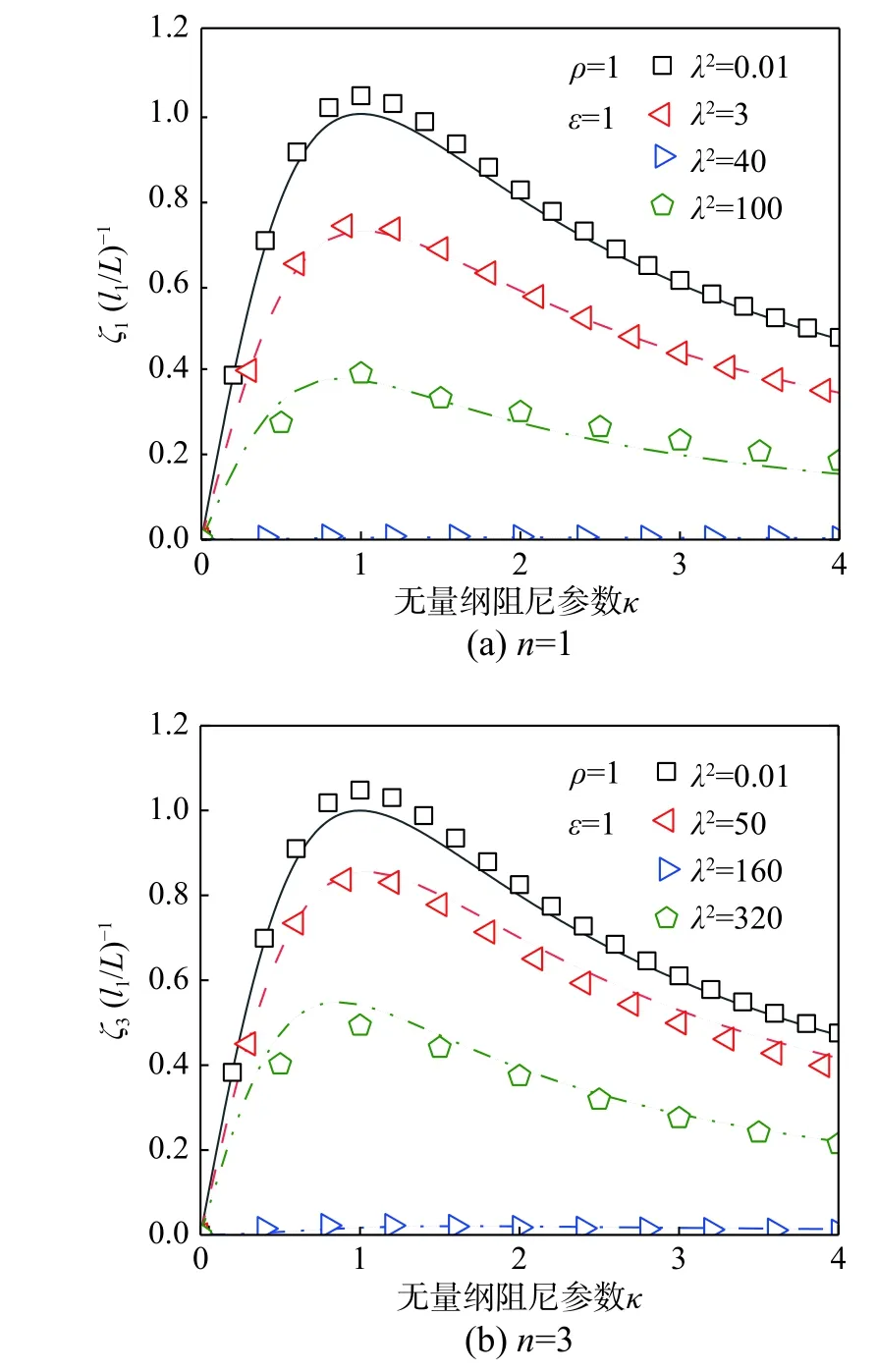
图2 不同 λ2 时系统模态阻尼曲线( l 1/L=0.02)Fig. 2 Damping curves for l 1/L=0.02 and varied values ofλ2

图2 给出不同的λ2下拉索一阶、三阶近似对称振型振动模态阻尼比曲线。由图2 可知，垂度对于模态阻尼比有较大的影响。当λ2=(n+1)2π2时出现“频率交叉”，此时阻尼器失效，文献[19]对这种现象做了详细的解释。拉索安装双阻尼器与安装单阻尼器规律是一致的，对于一阶、三阶近似对称振动模态，λ2分别为40、160 时系统模态阻尼比几乎为0，当λ2偏离这个值时，阻尼器效果将会提高。

分析λ2对拉索模态阻尼比的影响，图3 给出了拉索前5 阶模态下λ2与最大模态阻尼比的关系曲线。由图3 可知，垂度仅对拉索近似对称振型的最优模态阻尼比有影响。对于一阶、三阶、五阶模态，当垂度参数λ2=(n+1)2π2时，系统模态阻尼比降低到0，偏离这个值后，λ2增大或减小都会使模态阻尼比增大，这与图2 所得结论相一致。由图3 可知垂度仅对一阶振动模态阻尼比影响较大，对于三阶、五阶的影响较小。实际斜拉桥中拉索λ2一般不大于3，迪拜在建云溪塔的最长拉索，其垂度参数λ2达到10 以上[32]。当λ2=3时，垂度造成拉索的一阶模态阻尼比降低至不考虑垂度时的70%左右，当λ2=10时，降低至35%附近。可见垂度对于一阶模态阻尼影响非常显著。

图3 前五阶模态 λ2与最大模态阻尼的关系曲线Fig. 3 Dependence of maximum modal damping on the cable sag

为了研究拉索-双阻尼器系统近似对称振型振动下的动力特性，对式(22)进行分析。拉索两端安装阻尼器时系统模态阻尼曲线如图4 所示。λ2=3时，图4(a)给出同参数双阻尼器在不同相对安装位置时系统一阶模态阻尼比变化情况，双阻尼器安装位置参数 ρ的取值范围[0, 1]。图4(b)给出 ρ=3/4时两个阻尼器阻尼参数比对拉索模态阻尼比的影响情况。

图4 两端安装阻尼器系统一阶模态阻尼曲线Fig. 4 First modal damping curves of cable equipped with two dampers at the opposite cable ends

由图4(a)可知，拉索的模态阻尼比随着 ρ值的增大而增大。当 ρ=1 时 ，阻尼比 ζ(l1/L)-1约为ρ=0 时 的2 倍，即垂度λ2=3时安装双阻尼器较安装单阻尼器拉索的最大模态阻尼比提高了1 倍，对应2.1.3 节，可见安装双阻尼器对拉索减振效果的提高是十分显著的。图4(b)给出了 ρ=3/4时典型工况的系统阻尼曲线，并给出了更多工况下系统阻尼比的最优值点(圆点表示)。由分析结果可知，双阻尼器阻尼参数比的变化对拉索的减振有较大的影响。 ε=0表示拉索安装单个阻尼器，ε ＞0 后表示第二个阻尼器参与减振。随着 ε值的增大系统所获得的最大阻尼比先增大后减小，最大模态阻尼比点逆时针形成一个近似闭合的环。最大阻尼比存在最优值，即当 ε=1/ρ时，相关证明已在2.1.3 节中提及。当 ε变的无穷大时，意味着第二个阻尼器的阻尼系数无穷大，拉索在该位置处“锁定”，拉索仅是自由长度的减小，此时双阻尼器的减振效果近似于单个阻尼器。

3.2 近似对称振型同端布置

式(24)给出了拉索一端安装双阻尼器时系统一阶模态阻尼比计算公式，如图5 所示。

由图5(a)可见，拉索在同一位置安装2 个同参数的阻尼器( ρ=0、ε=1)与在该位置安装一个对应参数的阻尼器拉索所能获得的模态阻尼比是相同的，κ值约从1 将为0.5。所以，在拉索端部同位置安装双阻尼器并不能提高拉索的模态阻尼比，但可以减小每个阻尼器的尺寸。该结论与2.1.3 节对应一致。

从图5(a)的分析可知，拉索同一端安装双阻尼器对于共同抑制拉索的某一阶振动没有太大意义。而考虑单个阻尼器对拉索高阶振动控制的不足，讨论针对拉索高阶振动安装第二个阻尼器是有意义的。图5 进一步分析了固定阻尼器2，ρ=1(即l1=l2)，即在阻尼器2 与拉索近端锚固点中间的位置安装阻尼器1 时的系统阻尼变化情况。由图5(b)可知，当 ε趋于∞时，意味着阻尼器1 阻尼系数趋于0，相当于在拉索距锚固端l1+l2处安装单个阻尼器，此时 ζ(l1/L)-1最大。随着 ε的减小，即阻尼器1 的阻尼系数逐渐增大，当ε=0时，阻尼器1 阻尼系数趋于∞，拉索在阻尼器1 位置处“锁定”， ζ(l1/L)-1约降低到最大值的1/2。在 ε由大变小的过程中，最大模态阻尼(圆点表示)逐渐减小。由此可见，阻尼器1 的安装对于阻尼器2 的减振起到了负作用，并且阻尼器1 的阻尼系数越大负作用越明显，特别是当ε ＜1 时 。当 ε ＞1时，即阻尼器1 阻尼系数小于阻尼器2 的阻尼系数时，负作用较小。

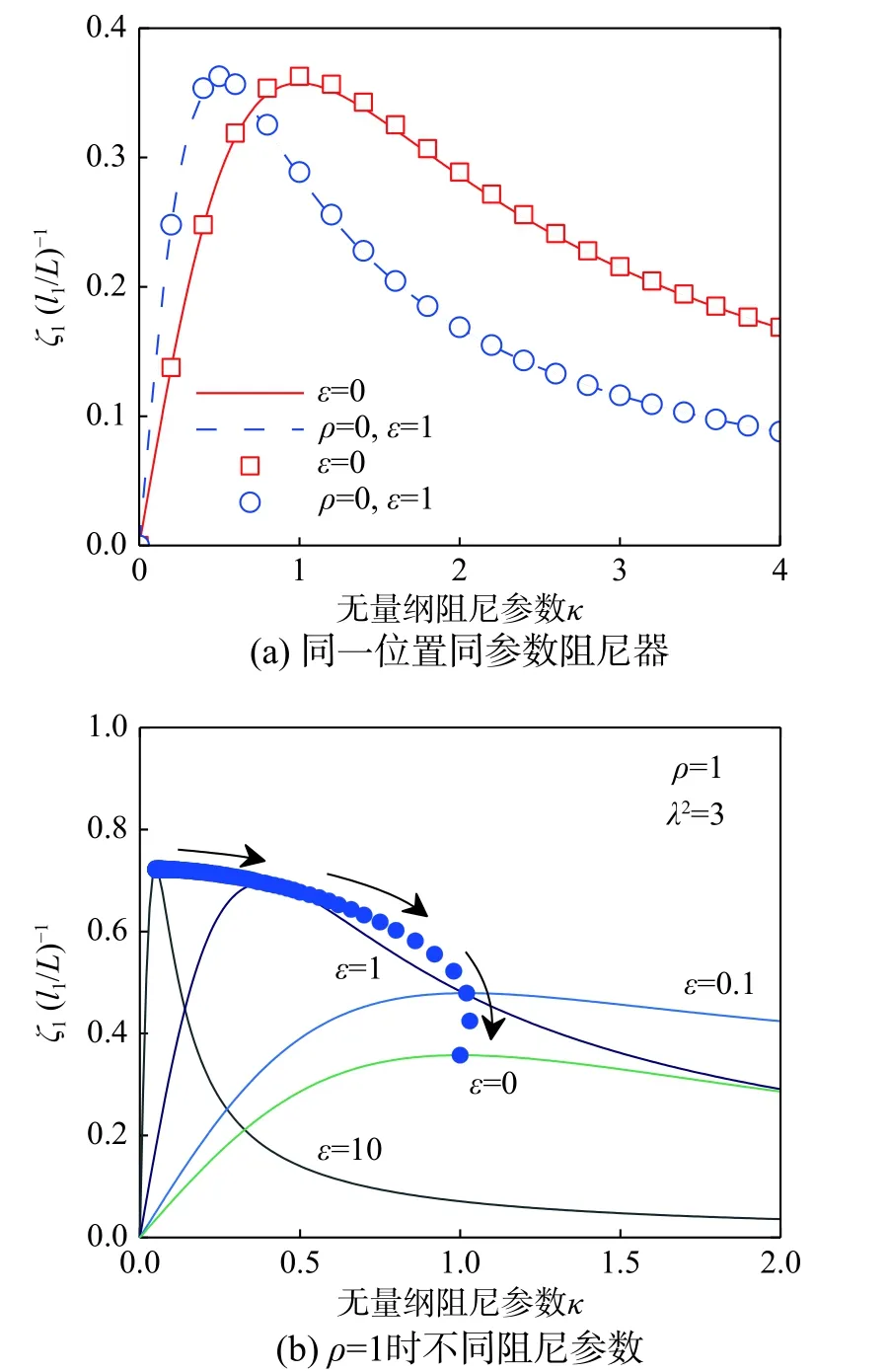
图5 同一端安装双阻尼器系统一阶模态阻尼曲线Fig. 5 First modal damping curves of cable equipped with two dampers at the same cable end

工程中对于拉索阻尼器的设计，通常是针对拉索的前几阶振动模态确定阻尼器参数[33]，无量纲参数，则阻尼曲线形式上不再重合在一起。针对前j阶模态进行粘滞阻尼器设计，第1 阶模态阻尼曲线与第j阶阻尼曲线的交点所对应的横坐标即为粘滞阻尼器优化阻尼参数值，如图6 所示。

图6 给出了拉索垂度参数λ2=3，单个阻尼器安装在 (l1+l2)/L=0.02时，针对拉索前5 阶振动阻尼器参数优化设计方法，此时阻尼器最优阻尼参数=0.61。为了研究双阻尼器在考虑多阶优化时对拉索多阶减振的效果，在l1/L=0.01的位置处增加一个同阻尼参数的粘滞阻尼器，参考图5(b)分析结果取=0.2379，分析前10 阶拉索模态阻尼的变化情况，如图7 所示。

图6 粘滞阻尼器多模态设计阻尼曲线Fig. 6 Damping ratio curves for design of viscous damper

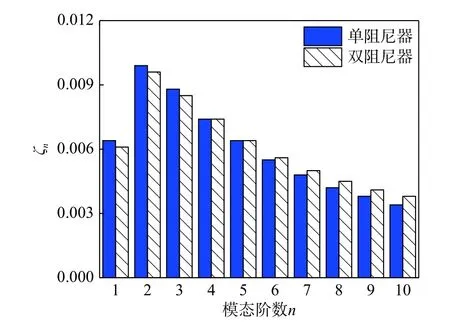
图7 安装单、双阻尼器减振效果对比Fig. 7 Comparison of two vibration control strategies

由图7 可知，粘滞阻尼器设计中考虑对拉索多阶控制的优化，安装双粘滞阻尼器对于控制较低阶振动是不利的，与前述分析一致，但是对高阶振动的控制却是有利的。

3.3 近似反对称振型两端布置

图8 给出了第二阶和第四阶模态拉索两端安装粘滞阻尼器的阻尼曲线，进一步验证了近似解的准确性。

图8 系统模态阻尼曲线Fig. 8 Asymptotic curves

为了研究拉索-双阻尼器系统近似反对称振型振动下的动力特性，对式(29)进行分析。与图4相类似，得到了如图9 所示的阻尼曲线。对于近似反对称振型，由于垂度对系统阻尼计算结果没有影响，后续阻尼曲线适用于任意阶近似反对称振型。

图9 基本规律与图4 相一致。对于近似反对称振型垂度没有影响，最优值大小可以由2.2.3 小节确定。

图9 两端安装阻尼器系统模态阻尼曲线Fig. 9 Modal damping curves of cable equipped with two dampers at the opposite cable ends

3.4 近似反对称振型同端布置

式(30)给出了拉索一端安装双阻尼器时系统模态阻尼比计算公式，分析如图10 所示。图10所得的结论与图5 相一致。

图10 同一端安装双阻尼器模态阻尼曲线Fig. 10 Modal damping curves of cable equipped with two dampers at the same cable end

4 结论

本文建立了有垂度拉索-双阻尼器系统模型，并推导出了在拉索近锚固端两个不同位置安装粘滞阻尼器时拉索模态阻尼比的近似解析式，近似公式可以为工程中超长拉索精确设计双阻尼器提供参考；在此基础上对双阻尼器参数进行了优化，同时分别研究了拉索两端安装和一端安装双阻尼器后拉索的振动特性，分析阻尼器参数关系对拉索模态阻尼的影响。研究结果表明：

(1)垂度仅对拉索对称振型有影响，对于反对称振型没有作用，且实际拉索垂度仅会对其一阶振动有较大影响。

(2)考虑拉索垂度的影响，两端对称安装阻尼器的阻尼效果约为单侧安装阻尼器时的两倍。

(3)同一端两处安装阻尼器不能提高拉索某一阶模态的最大阻尼比，但是对于同时抑制拉索高、低阶振动具有实际工程意义。