天然橡胶支座大变形压剪性能的双非线性超弹性理论和实验研究

杨 静，潘 文，苏何先，何颖成，管庆松，张岩岩

(1. 昆明理工大学建筑工程学院，云南，昆明 650500；2. 云南省抗震工程技术研究中心，云南，昆明 650500；3. 震安科技股份有限公司，云南，昆明 650000；4. 云南省设计院第五建筑设计有限公司，云南，昆明 650000)

国内外多次地震证实，隔震结构的减震效果非常明显。同时，考虑到未来需要对隔震建筑按更具体、更高的抗震设防目标进行性能化设计，隔震橡胶支座作为隔震结构的主要受力构件，有必要对其进行精细化分析研究。

隔震支座是由薄钢板和橡胶交替粘结在一起的复合构件，它作为结构的局部构件，当结构受到外部激励(静力荷载、外部动力或地面加速度)时，构件的反应量有位移、速度、加速度，对于地震激励，这些量的绝对值和相对值可能都是需要的；但与结构变形有关的相对位移最重要，只要支座每个受力状态的位移确定，其内力及应力就可由每一瞬时的静力分析确定[1]。因此，国内外学者基于静力状态对隔震橡胶支座进行了大量研究。

Haringx[2]是关于叠层橡胶支座性能的经典理论。该理论考虑了承受压缩载荷和水平变形构件的水平刚度和屈曲载荷。但是，由于Haringx 理论是在假设材料线弹性的情况下推导的，因此无法将其直接用于评估变形较大的叠层橡胶的非线性行为。而后，Kelly[3]同样基于材料线弹性假定，建立了数学物理模型并推导了隔震橡胶支座的水平刚度理论计算公式，并分析了支座的屈曲稳定。Chang 等[4]和Ding[5]分别采用解析刚度矩阵法和传递矩阵法，建立了离散的叠层橡胶支座的线性力学模型，该模型基于Haringx 理论，对具有不同几何参数和材料性能的支座进行逐层分析，计算内力和位移。但是，在考虑弯矩刚度及材料属性时，仍假设橡胶物理属性为线性 (E=3G)[6-7]，未能反映大变形材料特性的非线性行为。Takaoka[8]建立了一种基于Haringx 理论的叠层橡胶支座非线性力学模型，但该模型预测叠层橡胶支座的大变形行为精度需取决于橡胶层的抗弯刚度和抗剪刚度非线性参数的合理设置。

在此背景下，本文基于Haringx 理论提出了一种天然叠层橡胶支座大变形压剪状态的双非线性方法。它的特征是可以通过将材料非线性引入到支座等效匀质体的等效弹性模量Ec和弯曲刚度EcIs中，用EcA、EcIs表示支座变形的内力，建立微分平衡方程来表达大变形区域中的双非线性行为。同时，结合实际工程中生产的足尺隔震支座的压剪实验，验证了该方法的严密性和准确性。此外，隔震支座中橡胶属于高分子聚合物，生产硫化过程中，已与硫化剂发生化学反应，具备了较高的弹性、耐热性、延展性等[6-7]，可以认为隔震支座橡胶属于理想超弹性材料，即不考虑变形对时间、温度的依赖性。

目前，非线性固体力学的发展已经与材料微观结构的发展紧密结合[9]。本文研究对象为隔震橡胶支座，其中，橡胶在微观结构中存在明确的超弹性本构方程[10]。另外，一般物体在外力作用下会发生形状和尺寸的改变，剪切模量G和体积模量K正是与这两种不同类型的变形对应的两个基本模量[11]，其中，G反映物体形状的改变，K反映尺寸的变化。对于大多数材料，这两个模量属于同一量级，但是，对于特殊材料，如叠层隔震支座中的橡胶，其K值的量级则远大于G，因此其压缩变形将非常明显地依赖于任何可能阻止形状变化的边界条件[11-12]。综合考虑，有必要先从隔震叠层橡胶支座中隔离出单层橡胶进行受力分析。

1 单层橡胶单轴等效弹性模量和纯弯刚度的推导

橡胶属于各向同性材料[10]，因此，以下每个变形状态，橡胶内部各点的剪切模量G均相同[9]。

1.1 推导单轴等效弹性模量

1.1.1 假设纯压运动量，引入位移函数

在实际工程中，因隔震层平面内刚度及支座竖向刚度都很大，竖向压力作用下，竖向变形较均匀；且单层橡胶水平向受到上、下钢板较大的约束。根据以上特点，作如下2 条假设：

1) 橡胶各点变形过程中，水平面保持不变；

2) 变形前的垂直线受竖向力后，各点变形后为抛物线，其中垂直线两端与钢板接触各点无变形。物理坐标系如图1 所示。

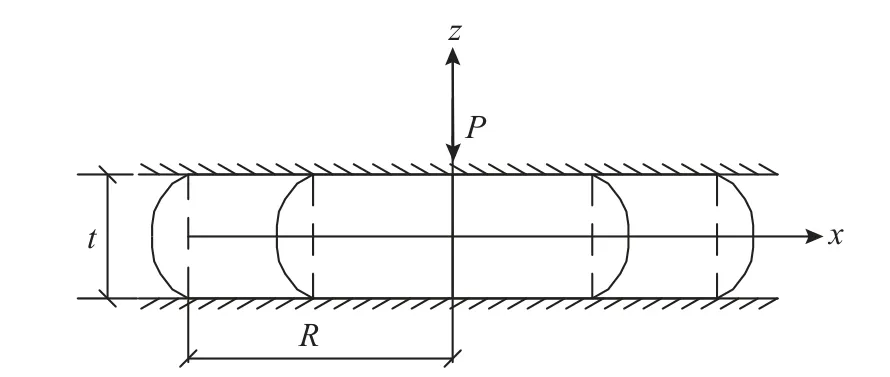
图1 单层橡胶纯压变形图Fig. 1 Single-layer rubber pure pressure deformation diagram

设未发生变形前，橡胶各点三维坐标为μ0(x,y),υ0(x,y),ω(z)。变形后，位移函数为：

1.1.2 推导等效弹性模量

根据橡胶支座变形过程中体积保持不变[7,13]，略去线应变更高阶的微量，其体应变为：

代入位移函数得：

在厚度t范围内，对变量z积分：

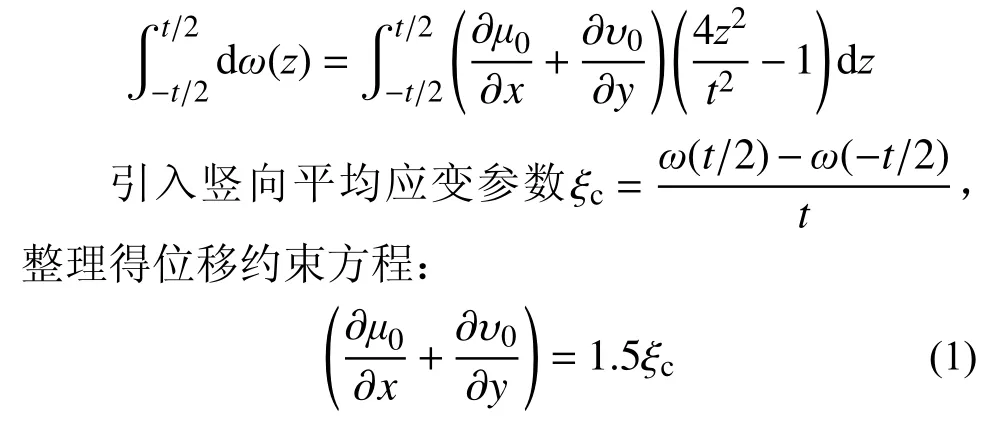
取单层橡胶任一点为微元体，其三维受力如图2 所示。

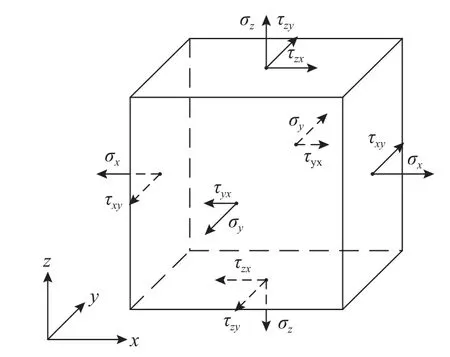
图2 微元体受力图Fig. 2 Micro-body force diagram

由几何方程计算切应变：

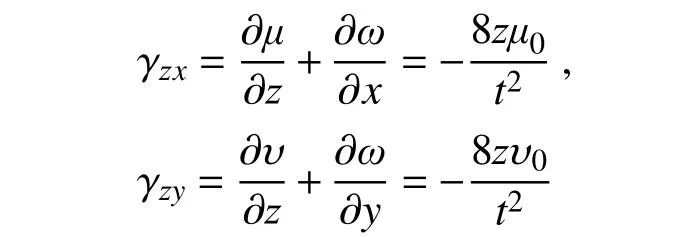
圆形橡胶支座的变形仅沿极坐标径向方向：

根据广义胡克定律：

代入x、y方向平衡微分方程：

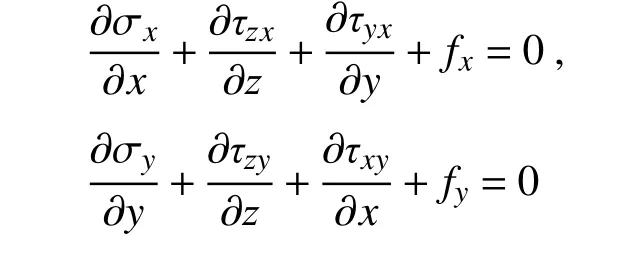
不考虑支座体力，得：

上两式各对x、y求导，代入式(1)，得：

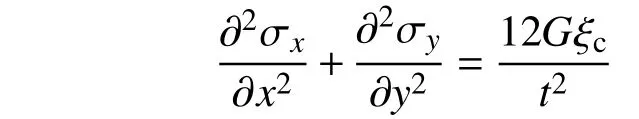
对于不可压缩弹性固体，有内部约束方程[10]：

式中： σ为应力张量；S为法向偏张量；p为受力方向主应力。支座受力状态处于非扭曲状态，Sx=0,Sy=0，有：

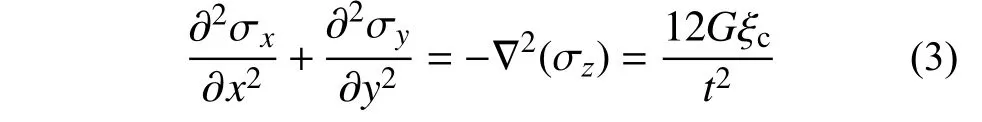
式(3)为应力 σz的调和函数[14]，即拉普拉斯算子，它的重要特点是，满足此算子的变量，即使固体受力状态属于大变形，当与其他符合调和函数的变量相加减时，仍符合线性叠加原理。

在极坐标下，拉普拉斯算子存在简单变换式[14]，且存在边界条件r=R时 ， σz=0，则：

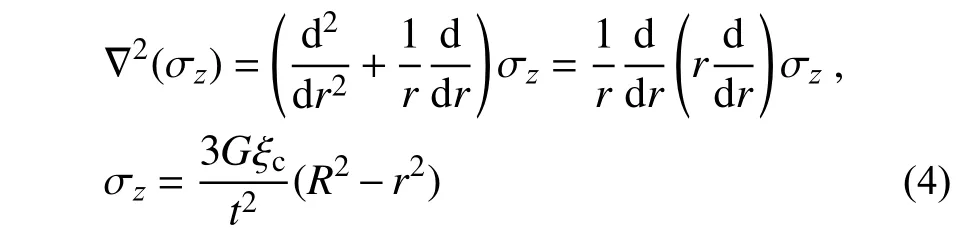
对式(4)两边在半径R范围内积分，得：

1.2 单层橡胶纯弯等效弯曲刚度的推导

由1.1 节结论所得Ec，就可进一步推导压剪支座与Ec相关的等效弯曲刚度。

1.2.1 假设纯弯运动量，修正位移函数

单层橡胶层受弯矩作用时，作如下假设：

1) 因钢板弯曲刚度很大，假设钢板保持平面转动，设相邻钢板之间的转角为 α；

上式对x求导，得：

不考虑y方向扭转，则有：

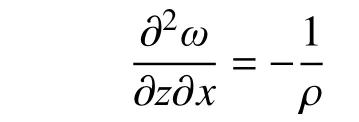
由边界条件z=0 时 ，ω=0, ∂ω/∂z=0，得：

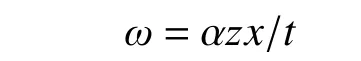
设未发生变形前，橡胶各点三维坐标为μ0(x,y), υ0(x,y),ω(z)；变形后，变形如图3，且位移函数为：

图3 单层橡胶纯弯变形图Fig. 3 Single-layer rubber pure bending deformation diagram

1.2.2 推导纯弯等效弯曲刚度

单层橡胶纯弯调和函数的推导同1.1.2 节纯轴压，则有：

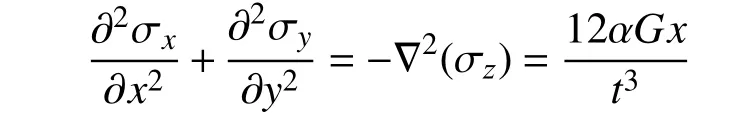
因弯曲关于y轴对称，并由边界条件，得竖向应力解析式：

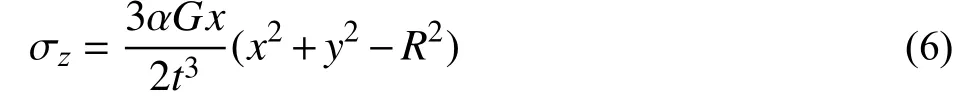
在极坐标下，应力对yz面求矩，并在整个截面上积分，求总截面弯矩：

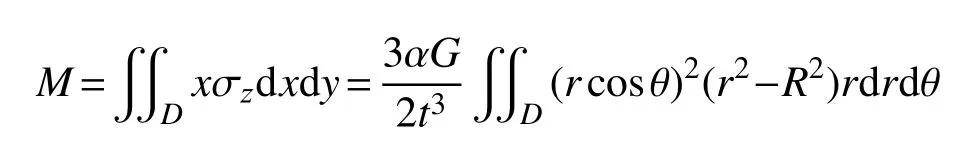
因截面转动 α较小，引入钢板转动曲率半径ρ，且截面直径 2R≥t，则有： α ρ=t,1/ρ=α/t。

由1.1 节推导结论Ec，有：

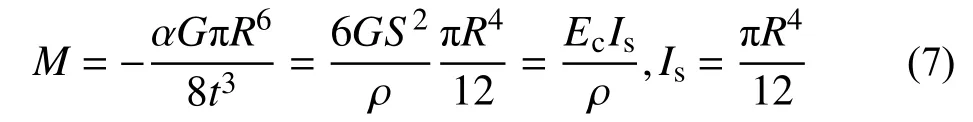
2 压剪隔震橡胶支座数学模型方程的建立与通用解答

2.1 假设运动量，建立数学物理方程，并求通解

非线性连续介质力学研究物质宏观层次的运动、变形与破坏，与微观层次相比它是一个更加复杂的系统，它受制于微观结构，又有自己独特的规律，描述宏观物体运动规律的方程一般是偏微分方程[9]。橡胶属于易变形的固体，由其与钢板交替粘结在一起的橡胶隔震支座，在竖向和水平荷载共同作用下会发生较大的水平位移和微小的弯曲变形，其运动形式简单明确，可以通过建立偏微分方程反映隔震橡胶支座宏观的运动、变形。

根据第1 节从橡胶微观结构推导的Ec与EcIs，可以假设叠层橡胶支座为符合Ec与EcIs的等效均质体；同时，考虑到支座中剪切变形基本上由橡胶产生，均质体的几何参数(As、Is)需考虑h/hr的放大系数[3](h为支座总高度、hr橡胶层总高度)。

在压剪作用下，叠层橡胶支座产生较大的水平剪切变形，故假设支座水平位移μ为第一个运动未知量。支座轴线还会产生弯曲变形，但因支座弯曲刚度较大，则横截面转动变化也较小，可认为横截面转动后仍保持平面，但与变形后轴线不垂直，这是橡胶支座大变形的重要特征。为表示支座的弯曲变形程度，引入横截面的转角 β为第二个运动未知量。在几何空间笛卡尔坐标系中(图4)，设坐标横轴为u，沿支座高度方向为坐标纵轴x。

根据弹性力学微元体几何方程的推导原理，把橡胶支座作为有限大固体[14]，如图5 所示，则最初相互垂直的线段OA与OB，运动到新平衡位置O′A′与O′B′时，二者之间角度的改变量θ，就是切应变。基于以上原理，将图4 中均质体的下部分离体出来，则在剖面处，新横截面上剪力为V=GAs(μ˙-β) ； 同时，转角的导数 β˙(即为轴线上该点的曲率)，则新横截面上弯矩为M=EcIsβ˙。由新截面上力的平衡及对中心点取矩，得平衡微分方程：

图4 均质体支座数学物理简图Fig. 4 Mathematics and physics diagram of homogeneous body support

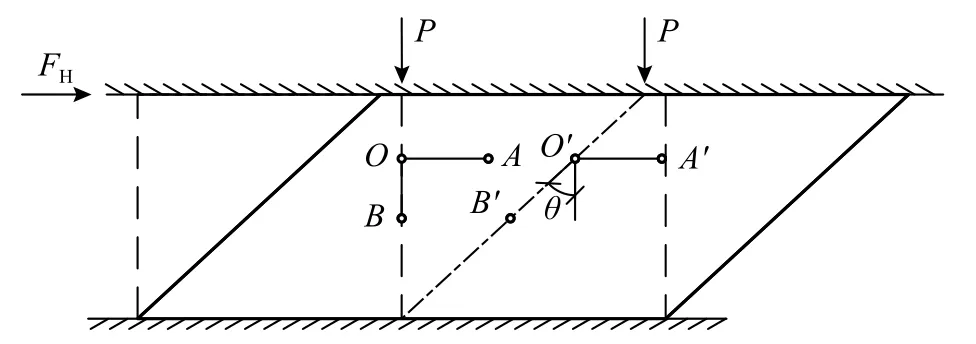
图5 有限大支座几何位移关系Fig. 5 Geometric displacement relations of finite bearings

因转角很小，则 cosβ →1, sinβ →β，以上超越方程可简化为：

将M、V代入式(8)、式(9)得二元一阶偏微分方程组：

求解关于μ、β的二元一阶偏微分平衡方程。

隔震橡胶支座未知运动量μ、β的通用解答为：

2.2 隔震橡胶支座运动量和内力的解析解

当支座上、下两端不限制转动时，式(12)、式(13)有未知常数A、B，其通解不能直接应用到隔震橡胶支座中。但因在实际工程中，橡胶隔震支座上、下截面分别与刚度较大的隔震层和下支墩相连接，相比之下，橡胶支座部分的剪切刚度较小，因此，支座数学物理模型简化时，可假定支座上、下截面为固定端。基于此假定，橡胶支座顶部在水平剪力与轴力共同作用下，则其运动量方程式(12)、式(13)的边界条件为：

代入边界条件，可求得方程中的未知常数：

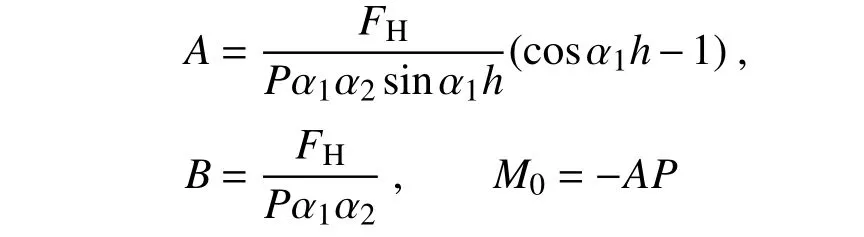
由此可知，在压剪共同作用下，橡胶隔震支座任一横截面水平位移μ与 转角 β有唯一解答(轴压P产 生的P-Δ效应，不需要反复迭代，即可求精确解)。且支座顶部的初始弯矩M0不独立，它是关于P、FH的函数，从另一角度，在物理意义上，以上结论可解释压剪支座满足变形协调方程。

最后，将所求运动量μ、β代入式(8)、式(9)，即得每个横截面处对应内力M、V：

3 隔震橡胶支座的理论解与实验结果对比分析

3.1 实验隔震橡胶支座

本压剪实验选取实际隔震工程中的天然橡胶支座，其尺寸见表1。表2 则通过假设在等截面条件下，支座等效均质体与其他常用材料(混凝土与钢材)的材料属性对比。可知等效均质支座的剪切刚度远小于钢材与混凝土，而弯曲刚度接近等截面混凝土。从另一个方面验证了第2 节中假定支座的剪切刚度很小、弯曲刚度很大是合理的。

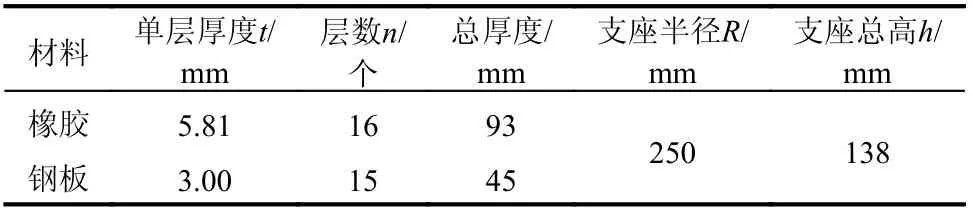
表1 橡胶支座尺寸Table 1 Size of rubber bearing

表2 等截面不同材料属性对比Table 2 Comparison of different material properties of equal section

3.2 隔震橡胶支座压剪实验与其 G的合理选取

本次实验加载设备为电液伺服压剪试验机(图6)，其最大轴向压力15 000 kN，水平最大动荷载1500 kN，竖向轴力按设计压应力12 MPa 保持不变，缓慢施加水平荷载，最大剪应变400%(相当于最大水平位移377 mm)[15-16]。为消除橡胶粘性、蠕变及松弛等[17-18]其他性质的影响，取支座的第一个往复运动的1/4 曲线。其中加载曲线局部不光滑的原因，由于实验设备受到了摩擦的影响[16]。

图6 动态压剪试验机Fig. 6 Dynamic compression shear testing machine

在非线性连续介质力学中，当固体受到较大的变形时，变形和未变形构型的位置关系用变形梯度张量表示，而材料属性与空间矢量关系通过柯西变形张量描述[10]。与初始状态相比，支座在不同剪应变时，位置与材料属性都发生较大改变。而由叠层橡胶支座实验所得水平力与竖向、水平位移推导的G，综合反映了支座在外力作用下，支座每个状态几何位置与材料属性的双非线性的改变。与1 节平衡微分方程中G反映了支座整体每个压剪状态的宏观G相一致。

3.3 隔震橡胶支座 FH-γ 与 G-γ理论、实验曲线对比分析

依据图7 所示框图，可由实验曲线上每个压剪状态 γ 对应的G，迭代计算出该状态橡胶支座的理论G与 γ值，同理，得出所有状态的外力与变形FH-γ 理论曲线(图8、图9)。对比可知，FH-γ的实验与理论曲线几乎100%重合，说明考虑橡胶为非线性超弹材料时，压剪隔震橡胶支座的理论解为精确解答。

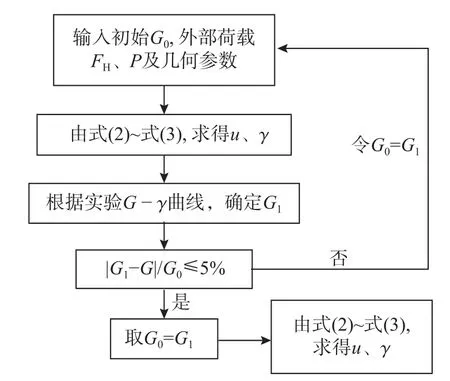
图7 剪切模量G 与剪应变 γ计算程序框图Fig. 7 Block diagram for calculation program of shear modulus G and shear strainγ

图8 隔震橡胶支座压剪 G-γ实验、理论曲线(P=12 MPa)Fig. 8 Compression-shear G -γ experiment and theoretical curve of vibration isolation rubber bearing (P=12 MPa)

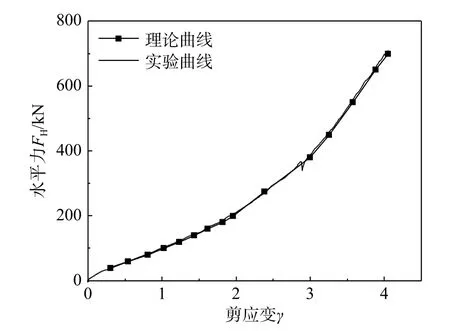
图9 隔震橡胶支座 FH-γ理论、实验曲线(P=12 MPa)Fig. 9 Compression-shear FH-γ experiment and theoretical curve of vibration isolation rubber bearing (P=12 MPa)

综上所述，考虑到橡胶支座的整体剪压变形和材料属性的共同影响，《建筑隔震橡胶支座》GB/T 20688.3-2006[15]在确定橡胶支座多遇地震( γ=100% ) 、罕遇地震( γ=250% ) 的 γ 对应G时，采用足尺橡胶支座进行实验是合理的。

4 隔震橡胶支座内力分布规律和剪应变、压力相关性分析

4.1 橡胶支座各内力与运动量分布图

基于前面系统的阐述推导，可对隔震支座某一个压剪状态进行受力分析，如隔震支座在最大水平推力FH=700 kN、P=12 MPa 作用下，可迭代计算出该状态 γ=400%、G=0.89 MPa，进而可得各截面运动量及内力值(图10)。由图可知，橡胶支座最大水平位移出现在顶端，最大弯矩在支座两端，最大剪力与转角在支座中部。横截面转动角度均小于 1 ( 1=0.017 rad)，此处验证了第2 节中假定匀质体的转动角度 β较小是符合实际情况的。这些结论对于判断支座产生破环的具体位置有一定的参考价值[19]。

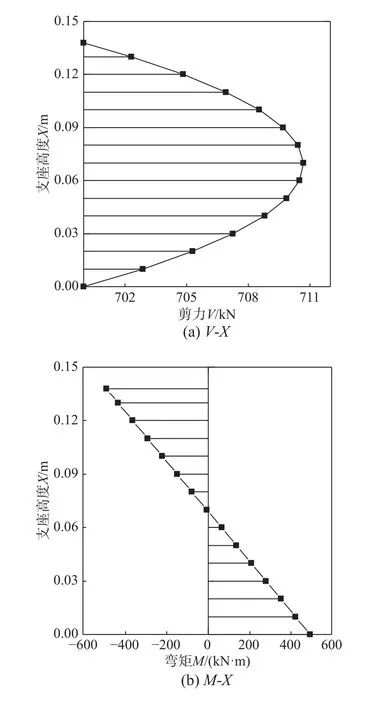
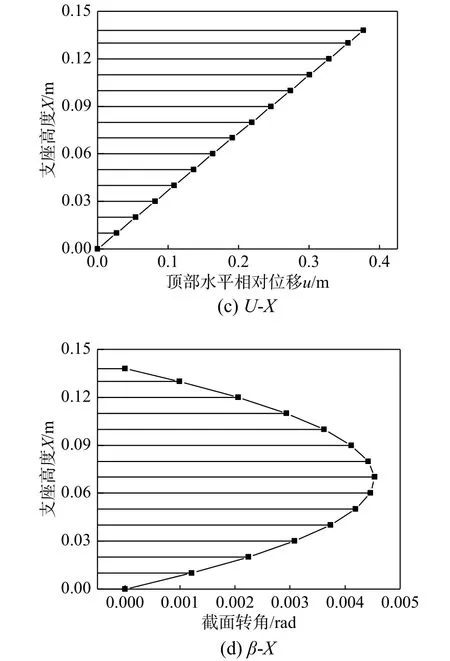
图10 沿截面高度内力 M、V 及运动量 μ 、β的分布图Fig. 10 Distribution diagram of internal force M、V and movement amount μ 、β along the section height

4.2 橡胶支座剪应变相关性分析

4.1 节中确定了橡胶支座最大内力所在的危险截面，将结论代入式(4)、式(6)及式(7)，可进一步确定此截面内各点的竖向应力。不同剪应变下，支座顶部沿水平推力轴线竖向应力分布图11(P=12 MPa)。由图可知，随剪应变的增加，橡胶支座顶端截面压应力较大区域的竖向压应力逐渐增大，压应力小的区域压应力减小逐渐变为拉应力，且拉应力随剪应变增加，绝对值也增加。但支座中心点的压应力为定值，大小为2P/A[20]。

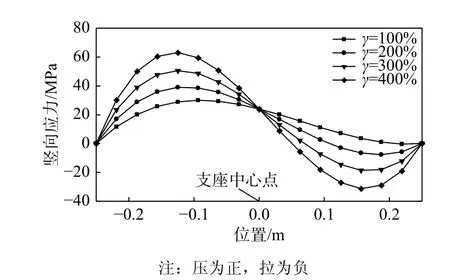
图11 轴压不变、不同剪应变时橡胶支座竖向应力分布图Fig. 11 The vertical stress distribution diagram of the rubber bearing when the axial pressure is constant and the shear strain is different

4.3 轴压变化引起效应P-Δ 与内力变化规律

为反映轴力变化对橡胶支座顶部水平位移及内力影响，仍选取4.1 节中支座的这一受力状态(剪应变400%、轴压应力P=12 MPa、G=0.89 MPa)。因剪应变不变，且实验轴压与设计压应力差别不大时，橡胶G受压力的影响较小，则不同轴力下，可不考虑支座G的变化[15]。将外力及G代入式(12)～式(14)，可得支座内力与位移理论解，且随轴力的变化规律如图12、表3 所示。

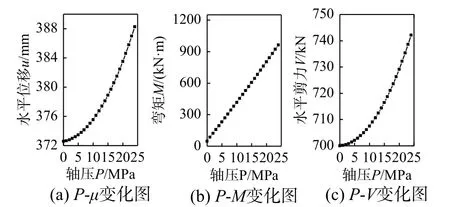
图12 不同轴压，支座顶端水平位移与内力变化图Fig. 12 The horizontal displacement of the top of the support and the internal force change diagram under different axial pressure

表3 不同轴力下，支座顶部截面内力与水平位移理论值Table 3 The theoretical values of the internal force and horizontal displacement of the top section of the support,under different axial forces

由以上图表可知，随橡胶支座轴力增大，水平位移呈非线性增加，但增加比例不大，即P-Δ效应不明显，但是，支座端弯矩增加较大，因此橡胶内应力随轴压的变化不可忽视[21-24]。

4.4 压应力相关性分析

从图13～图15 可知，当剪应变越大时，轴压改变引起竖向应力的变化越明显，即压力相关性强；而当剪应变小时，轴压变化引起竖向应力的变化不明显，即压力相关性弱。

图13 剪应变100%、不同轴压支座顶部竖向应力变化图Fig. 13 The vertical stress change diagram on the top of the support, with 100% shear strain and different axial compression

图14 剪应变400%、不同轴压支座顶部竖向应力变化图Fig. 14 The vertical stress change diagram on the top of the support, with 400% shear strain and different axial compression

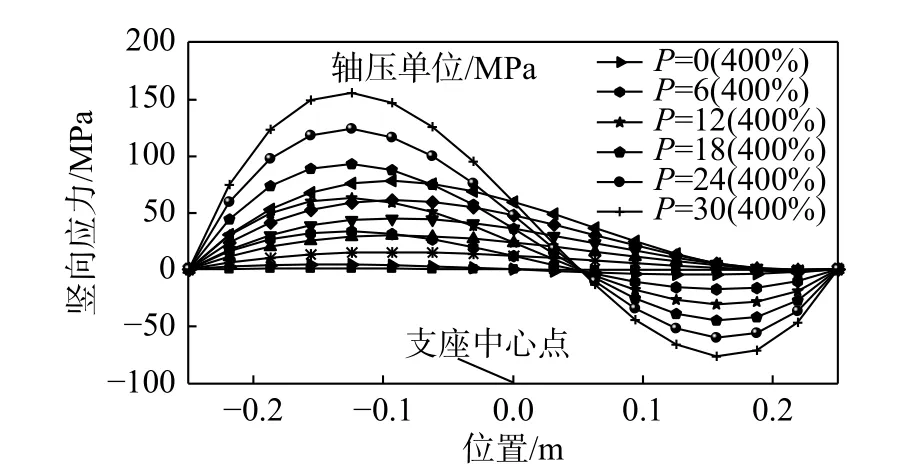
图15 剪应变100%、400%，不同轴压下支座顶部竖应力对比图Fig. 15 Comparison of the vertical stress on the top of the support, when the shear strain is 100%, 400%,and different axial compressions

5 纯剪隔震橡胶支座数学模型方程的建立与通用解答

当竖向轴力P=0，支座仅受水平力FH作用时，由于原微分方程中没有了运动量的一次项，微分方程需要重新求解。

将P=0 代入式(10)、式(11)，得：

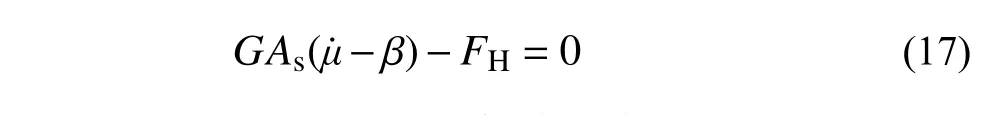
求解方程并由边界条件得未知运动量及截面内力解答：

由式(18)可知，x=h时，支座顶部水平位移最大，即：

式(20)中第一项为弯曲引起的位移μE，对于长度远大于横截面尺寸的构件，其水平位移可以仅考虑第一项弯曲的影响，如工程中不考虑轴力影响的层间柱抗弯刚度；第二项为剪力贡献的位移μG，对于高度与横截面尺寸相近，而材料参数GAs≪EcIs的构件，第二项提供了较大位移，如此文中的隔震橡胶支座，在水平力FH=700 kN 作用下，各项结果见表4，且可知式(20)与式(10)、式(11)在P=0 极限解答(见表3)相同。

表4 纯剪切内力与位移理论值Table 4 Theoretical values of internal force and displacement in pure shear

6 结论

本文采用将橡胶材料的微观结构和叠层橡胶支座的宏观运动、变形相结合的方法，从数学的角度，结合物理运动学与静力学，先后以单层橡胶和支座整体为研究对象，最后用关键性实验来验证理论结果，合理解释了在水平、竖向荷载耦合作用下橡胶支座的几何、材料双非线性的大变形特征。主要得到以下结论：

(1) 根据单层橡胶推导结果的GAs与EcIs，建立了橡胶支座在两种外部荷载同时作用下，反映水平变形与弯曲程度的偏微分平衡方程，得到了橡胶支座大剪切变形下，竖向与水平两种荷载耦合作用下大剪切变形的几何非线性通用解答。

(2) 因橡胶是各向同性材料，每个剪应变状态，宏观上支座有相同的剪切模量，但不同剪应变有不同的剪切模量。因此，确定各个状态叠层橡胶支座的剪切模量非常重要。在第(1)部分理论解答基础上，开展了实际工程中橡胶支座的压剪实验，依据实验G-γ 曲线，得到支座FH-γ的理论曲线，与FH-γ实验曲线几乎完全重叠，解决了超弹性橡胶支座大剪切变形的材料非线性问题。

(3) 根据以上理论，对隔震支座某压剪状态进行受力分析，得到支座各截面运动量与内力解析式，可知，橡胶支座最大水平位移出现在顶端，最大弯矩在支座两端，最大剪力与转角在支座中部。这些结论对于判断支座产生破环的具体位置有很好的参考价值。

(4) 剪应变不变，考虑轴力变化，得到以下规律，随橡胶支座轴力增大，水平位移呈非线性增加，但增加比例不大，即P-Δ效应不明显；而支座端弯矩增加较大，因而橡胶内应力随轴压的变化不可忽视。

(5) 为了验证不同剪应变时，轴压相关性的强弱，分别在剪应变100%、400%，施加变化的轴力，对比表明，当剪应变越大时，轴压改变引起竖向应力的变化越明显，即压力相关性强；而当剪应变小时，轴压变化引起竖向应力的变化不明显，即压力相关性弱。